Generate and return the cross-correlation function (CCF) (f\star g)(\tau) of the discrete signal g lagging the signal the discrete signal f for a range of specified lags.
This generic interface a flexible wrapper for the lower-level potentially faster generic interface setCCF.
See the documentation of the parent module pm_sampleCCF for algorithmic details and cross-correlation definition.
- Note
- The input sequences
f and g are right-padded with zeros to a minimum length of max(lag(size(lag)), size(f) - 1) - min(lag(1), 1 - size(g)) + 1 before computing the cross-correlation.
- Parameters
-
| [in] | f | : The input contiguous vector of arbitrary size (of minimum 2) of,
-
type
complex of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128),
-
type
real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128),
containing the first sequence in the cross-correlation computation.
|
| [in] | g | : The input contiguous vector of arbitrary size (of minimum 2) of the same type and kind as the input argument f, containing the second sequence in the cross-correlation computation.
|
| [in] | lag | : The input vector of type integer of default kind IK of arbitrary size, containing the set of lags in ascending order for which the correlation must be computed.
(optional. default = getRange(1 - size(g), size(f) - 1)) |
| [in] | norm | : The input scalar constant that can be:
-
the constant nothing or an object of type nothing_type, implying that the input
f and g must be used as is without any normalization.
-
the constant meanshift or an object of type meanshift_type, implying that the input
f and g must be mean-shifted before computing the cross-correlation.
-
the constant stdscale or an object of type stdscale_type, implying that the input
f and g must be scaled by a factor of 1 / sqrt(sum(abs(f)**2)) / sqrt(sum(abs(g)**2)).
This option is particularly useful when the input sequences are already mean-shifted but not properly scaled.
-
the constant zscore or an object of type zscore_type, implying that the input
f and g must be mean-shifted and further scaled by a factor of 1 / sqrt(sum(abs(f)**2)) / sqrt(sum(abs(g)**2)).
(optional, default = zscore.) |
- Returns
ccf : The output allocatable vector of the same type and kind as the input f of size max(lag(size(lag)), size(f) - 1) - min(lag(1), 1 - size(g)) + 1, containing the cross-correlation of the input sequences f and g.
Possible calling interfaces ⛓
ccf(:)
= getCCF(f(:), g(:), lag
= lag, norm
= norm)
Generate and return the cross-correlation function (CCF) of the discrete signal lagging the signal ...
This module contains classes and procedures for computing properties related to the cross correlation...
- Warning
- The condition
isAscending(lag) must hold for the corresponding input arguments.
This generic interface is merely a flexible wrapper around the generic subroutine interface setCCF.
As such, all conditions and warnings associated with setCCF equally apply to this generic interface.
- See also
- getACF
setACF
getCCF
setCCF
getCor
setCor
getRho
setRho
getCov
setCov
setECDF
getMean
setMean
getShifted
setShifted
getVar
setVar
Example usage ⛓
23 type(display_type) :: disp
24 character(:),
allocatable :: format
25 integer(IK) :: nsam, shift, itry, ntry
= 1
29 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
30 call disp%show(
"!Compute the cross-correlation of two samples.")
31 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
36 integer(IK),
allocatable :: lag(:)
37 real(TKG),
allocatable :: f(:), g(:)
38 real(TKG),
allocatable ::
range(:), ccf(:)
40 call disp%show(
"nsam = 41; shift = nsam")
41 nsam
= 41; shift
= nsam
42 call disp%show(
"range = getLinSpace(-10., 10., nsam)")
58 call disp%show(
"lag = getRange(-nsam + 1, nsam - 1)")
60 call disp%show(
"ccf = getCCF(f, g, lag)")
66 call disp%show(
"if (0 /= getErrTableWrite(SK_'getCCF.crd.sin.cos.RK.txt', reshape([range, f, g], [nsam, 3_IK]), header = SK_'crd,f,g')) error stop 'ccf outputting failed.'")
67 if (
0 /= getErrTableWrite(SK_
'getCCF.crd.sin.cos.RK.txt',
reshape([range, f, g], [nsam,
3_IK]), header
= SK_
'crd,f,g'))
error stop 'ccf outputting failed.'
68 call disp%show(
"if (0 /= getErrTableWrite(SK_'getCCF.ccf.sin.cos.RK.txt', reshape([real(lag, TKG), ccf], [size(lag), 2]), header = SK_'lag,ccf')) error stop 'ccf outputting failed.'")
69 if (
0 /= getErrTableWrite(SK_
'getCCF.ccf.sin.cos.RK.txt',
reshape([
real(lag, TKG), ccf], [
size(lag),
2]), header
= SK_
'lag,ccf'))
error stop 'ccf outputting failed.'
75 complex(TKG),
allocatable :: f(:), g(:)
76 complex(TKG),
allocatable ::
range(:), ccf(:)
77 format = getFormat(deliml
= '', subsep
= SK_
'', delimr
= 'i', subcount
= 2_IK, signed
= .true._LK)
79 call disp%show(
"nsam = 41; shift = nsam")
80 nsam
= 41; shift
= nsam
81 call disp%show(
"range = cmplx(getLinSpace(-10., 10., nsam), getLinSpace(10., -10., nsam), TKG)")
86 call disp%show( f ,
format = format )
90 call disp%show( g ,
format = format )
91 call disp%show(
"ccf = getCCF(f, g, norm = stdscale)")
92 ccf
= getCCF(f, g, norm
= stdscale)
94 call disp%show( ccf ,
format = format )
Generate and return an array of the specified rank and shape of arbitrary intrinsic type and kind wit...
Generate a resized copy of the input array by padding it to the right with the requested paddings and...
Generate minimally-spaced character, integer, real sequences or sequences at fixed intervals of size ...
Allocate or resize (shrink or expand) an input allocatable scalar string or array of rank 1....
Generate count evenly spaced points over the interval [x1, x2] if x1 < x2, or [x2,...
Generate the natural logarithm of probability density function (PDF) of the univariate Normal distrib...
Generate and return a scalar or a contiguous array of rank 1 of length s1 of randomly uniformly distr...
Generate and return the iostat code resulting from writing the input table of rank 1 or 2 to the spec...
This is a generic method of the derived type display_type with pass attribute.
This is a generic method of the derived type display_type with pass attribute.
Generate and return the (weighted) mean of an input sample of nsam observations with ndim = 1 or 2 at...
Generate a sample of shape (nsam), or (ndim, nsam) or (nsam, ndim) that is normalized by the specifie...
Generate a sample of shape (nsam), or (ndim, nsam) or (nsam, ndim) that is shifted by the specified i...
Generate and return the variance of the input sample of type complex or real of shape (nsam) or (ndim...
This module contains procedures and generic interfaces for convenient allocation and filling of array...
This module contains procedures and generic interfaces for resizing an input array and padding them w...
This module contains procedures and generic interfaces for generating ranges of discrete character,...
This module contains procedures and generic interfaces for resizing allocatable arrays of various typ...
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
This module contains classes and procedures for computing various statistical quantities related to t...
This module contains classes and procedures for computing various statistical quantities related to t...
This module contains classes and procedures for input/output (IO) or generic display operations on st...
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
integer, parameter LK
The default logical kind in the ParaMonte library: kind(.true.) in Fortran, kind(....
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
This module contains classes and procedures for computing the first moment (i.e., the statistical mea...
This module contains classes and procedures for normalizing univariate or multivariate samples by arb...
This module contains classes and procedures for shifting univariate or multivariate samples by arbitr...
This module contains classes and procedures for computing the properties related to the covariance ma...
Generate and return an object of type display_type.
Example Unix compile command via Intel ifort compiler ⛓
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example Windows Batch compile command via Intel ifort compiler ⛓
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
Example Unix / MinGW compile command via GNU gfortran compiler ⛓
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example output ⛓
11+0.544021070,
+0.751511157E-1,
-0.412118495,
-0.798487127,
-0.989358246,
-0.937999964,
-0.656986594,
-0.215119988,
+0.279415488,
+0.705540299,
+0.958924294,
+0.977530122,
+0.756802440,
+0.350783229,
-0.141120002,
-0.598472178,
-0.909297407,
-0.997494996,
-0.841470957,
-0.479425550,
+0.00000000,
+0.479425550,
+0.841470957,
+0.997494996,
+0.909297407,
+0.598472178,
+0.141120002,
-0.350783229,
-0.756802440,
-0.977530122,
-0.958924294,
-0.705540299,
-0.279415488,
+0.215119988,
+0.656986594,
+0.937999964,
+0.989358246,
+0.798487127,
+0.412118495,
-0.751511157E-1,
-0.544021130
14-0.839071512,
-0.997172177,
-0.911130250,
-0.602011919,
-0.145500034,
+0.346635342,
+0.753902256,
+0.976587594,
+0.960170269,
+0.708669782,
+0.283662170,
-0.210795790,
-0.653643608,
-0.936456680,
-0.989992499,
-0.801143646,
-0.416146815,
+0.707371980E-1,
+0.540302277,
+0.877582550,
+1.00000000,
+0.877582550,
+0.540302277,
+0.707371980E-1,
-0.416146815,
-0.801143646,
-0.989992499,
-0.936456680,
-0.653643608,
-0.210795790,
+0.283662170,
+0.708669782,
+0.960170269,
+0.976587594,
+0.753902256,
+0.346635342,
-0.145500034,
-0.602011919,
-0.911130250,
-0.997172177,
-0.839071512
19-0.204734895E-1,
-0.275238696E-1,
-0.102999024E-1,
+0.315212049E-1,
+0.865425318E-1,
+0.134722009,
+0.153887838,
+0.127707034,
+0.525350161E-1,
-0.592308939E-1,
-0.180715948,
-0.277027875,
-0.315060228,
-0.273930311,
-0.152924940,
+0.256845243E-1,
+0.220294848,
+0.379635483,
+0.456209034,
+0.419997245,
+0.268570483,
+0.304476935E-1,
-0.239791244,
-0.473957509,
-0.607444108,
-0.596824765,
-0.433117509,
-0.146818906,
+0.197216138,
+0.514369488,
+0.721072078,
+0.756713450,
+0.600930333,
+0.281441927,
-0.130185992,
-0.534432232,
-0.827878892,
-0.929619253,
-0.803285122,
-0.468756527,
-0.108461009E-7,
+0.468756557,
+0.803285241,
+0.929619253,
+0.827878892,
+0.534432173,
+0.130185932,
-0.281441927,
-0.600930333,
-0.756713450,
-0.721072197,
-0.514369607,
-0.197216153,
+0.146818981,
+0.433117658,
+0.596824765,
+0.607443988,
+0.473957509,
+0.239791244,
-0.304477122E-1,
-0.268570572,
-0.419997245,
-0.456209034,
-0.379635453,
-0.220294803,
-0.256843958E-1,
+0.152925074,
+0.273930341,
+0.315060318,
+0.277027905,
+0.180715933,
+0.592308566E-1,
-0.525351278E-1,
-0.127707124,
-0.153887779,
-0.134722084,
-0.865425542E-1,
-0.315212607E-1,
+0.102998102E-1,
+0.275239069E-1,
+0.204736143E-1
25-0.204734895E-1,
-0.275238696E-1,
-0.102999024E-1,
+0.315212049E-1,
+0.865425318E-1,
+0.134722009,
+0.153887838,
+0.127707034,
+0.525350161E-1,
-0.592308939E-1,
-0.180715948,
-0.277027875,
-0.315060228,
-0.273930311,
-0.152924940,
+0.256845243E-1,
+0.220294848,
+0.379635483,
+0.456209034,
+0.419997245,
+0.268570483,
+0.304476935E-1,
-0.239791244,
-0.473957509,
-0.607444108,
-0.596824765,
-0.433117509,
-0.146818906,
+0.197216138,
+0.514369488,
+0.721072078,
+0.756713450,
+0.600930333,
+0.281441927,
-0.130185992,
-0.534432232,
-0.827878892,
-0.929619253,
-0.803285122,
-0.468756527,
-0.108461009E-7,
+0.468756557,
+0.803285241,
+0.929619253,
+0.827878892,
+0.534432173,
+0.130185932,
-0.281441927,
-0.600930333,
-0.756713450,
-0.721072197,
-0.514369607,
-0.197216153,
+0.146818981,
+0.433117658,
+0.596824765,
+0.607443988,
+0.473957509,
+0.239791244,
-0.304477122E-1,
-0.268570572,
-0.419997245,
-0.456209034,
-0.379635453,
-0.220294803,
-0.256843958E-1,
+0.152925074,
+0.273930341,
+0.315060318,
+0.277027905,
+0.180715933,
+0.592308566E-1,
-0.525351278E-1,
-0.127707124,
-0.153887779,
-0.134722084,
-0.865425542E-1,
-0.315212607E-1,
+0.102998102E-1,
+0.275239069E-1,
+0.204736143E-1
26if (
0 /= getErrTableWrite(SK_
'getCCF.crd.sin.cos.RK.txt',
reshape([range, f, g], [nsam,
3_IK]), header
= SK_
'crd,f,g'))
error stop 'ccf outputting failed.'
27if (
0 /= getErrTableWrite(SK_
'getCCF.ccf.sin.cos.RK.txt',
reshape([
real(lag, TKG), ccf], [
size(lag),
2]), header
= SK_
'lag,ccf'))
error stop 'ccf outputting failed.'
30nsam
= 41; shift
= nsam
34+5991.43115-9240.88965i,
+501.999237-6660.97363i,
-1669.71533-3691.48242i,
-1962.18994-1479.37476i,
-1474.61780-216.864731i,
-847.972107+313.365570i,
-360.236938+413.376801i,
-71.5428009+324.783783i,
+56.3624725+193.678986i,
+86.3214493+86.7014389i,
+71.1617279+21.0486450i,
+44.0026550-9.48644638i,
+20.6669369-17.8378811i,
+5.81346893-15.4914541i,
-1.42074847-9.91762066i,
-3.67000413-4.84708261i,
-3.42095494-1.50930655i,
-2.34651685+0.150619254i,
-1.29845750+0.634963870i,
-0.540612698+0.457304120i,
+0.00000000+0.00000000i,
+0.540612698-0.457304120i,
+1.29845750-0.634963870i,
+2.34651685-0.150619254i,
+3.42095494+1.50930655i,
+3.67000413+4.84708261i,
+1.42074847+9.91762066i,
-5.81346893+15.4914541i,
-20.6669369+17.8378811i,
-44.0026550+9.48644638i,
-71.1617279-21.0486450i,
-86.3214493-86.7014389i,
-56.3624725-193.678986i,
+71.5428009-324.783783i,
+360.236938-413.376801i,
+847.972107-313.365570i,
+1474.61780+216.864731i,
+1962.18994+1479.37476i,
+1669.71533+3691.48242i,
-501.999237+6660.97363i,
-5991.43115+9240.88965i
37-9240.88965-5991.43115i,
-6660.97363-501.999237i,
-3691.48242+1669.71533i,
-1479.37476+1962.18994i,
-216.864761+1474.61755i,
+313.365784+847.971619i,
+413.377441+360.236359i,
+324.785309+71.5424652i,
+193.681351-56.3617821i,
+86.7043381-86.3185654i,
+21.0505581-71.1552582i,
-9.48878765-43.9918022i,
-17.8498516-20.6530781i,
-15.5197325-5.80287600i,
-9.96691036+1.41372252i,
-4.91284418+3.62087893i,
-1.56562591+3.29789472i,
+0.166402861+2.12394547i,
+0.833729923+0.988897681i,
+0.989584863+0.249826387i,
+1.00000000-0.00000000i,
+0.989584863+0.249826387i,
+0.833729923+0.988897681i,
+0.166402861+2.12394547i,
-1.56562591+3.29789472i,
-4.91284418+3.62087893i,
-9.96691036+1.41372252i,
-15.5197325-5.80287600i,
-17.8498516-20.6530781i,
-9.48878765-43.9918022i,
+21.0505581-71.1552582i,
+86.7043381-86.3185654i,
+193.681351-56.3617821i,
+324.785309+71.5424652i,
+413.377441+360.236359i,
+313.365784+847.971619i,
-216.864761+1474.61755i,
-1479.37476+1962.18994i,
-3691.48242+1669.71533i,
-6660.97363-501.999237i,
-9240.88965-5991.43115i
38ccf
= getCCF(f, g, norm
= stdscale)
40-0.473868695E-7+0.316060185i,
-0.710963866E-8+0.336465567i,
-0.472260169E-7+0.241916165i,
-0.229052617E-7+0.133755907i,
+0.00000000+0.533953942E-1i,
+0.118386749E-7+0.763662765E-2i,
+0.555902986E-7-0.115134176E-1i,
+0.509577731E-7-0.150661031E-1i,
+0.370602002E-7-0.118032303E-1i,
-0.411779979E-7-0.702273846E-2i,
-0.181183196E-6-0.313396845E-2i,
-0.461193594E-6-0.752774591E-3i,
-0.823559958E-6+0.351545314E-3i,
-0.108696656E-5+0.651146576E-3i,
-0.937589107E-6+0.563895504E-3i,
+0.257165880E-6+0.360735052E-3i,
+0.329831255E-5+0.176593268E-3i,
+0.887923034E-5+0.552943311E-4i,
+0.167184462E-4-0.612265376E-5i,
+0.242153819E-4-0.268634976E-4i,
+0.246743402E-4-0.263549482E-4i,
+0.561013167E-5-0.181685045E-4i,
-0.508706908E-4-0.964594619E-5i,
-0.162461118E-3-0.357836802E-5i,
-0.331916672E-3-0.247067987E-6i,
-0.518805464E-3+0.105415677E-5i,
-0.599116087E-3+0.118592641E-5i,
-0.323401677E-3+0.938858363E-6i,
+0.692604517E-3+0.510607208E-6i,
+0.288338843E-2+0.238832399E-6i,
+0.646119658E-2+0.617669969E-7i,
+0.108593758E-1-0.185301001E-7i,
+0.138613293E-1-0.450384370E-7i,
+0.105927465E-1-0.350012996E-7i,
-0.702594826E-2-0.267656990E-7i,
-0.491255634E-1-0.622817211E-7i,
-0.123059995-0.437516228E-7i,
-0.222571239-0.272804250E-7i,
-0.309559852-0.168250729E-7i,
-0.290786266-0.169859238E-7i,
+0.110546567E-7+0.480133906E-7i,
+0.290786266+0.164711995E-7i,
+0.309559852+0.432368985E-7i,
+0.222571194+0.411779988E-8i,
+0.123060033-0.102944995E-7i,
+0.491255820E-1+0.205889990E-7i,
+0.702595199E-2+0.185301001E-7i,
-0.105927549E-1+0.370602002E-7i,
-0.138613135E-1+0.329423990E-7i,
-0.108593768E-1+0.308834984E-7i,
-0.646117283E-2-0.452957991E-7i,
-0.288338307E-2-0.230596797E-6i,
-0.692621863E-3-0.494135975E-6i,
+0.323413027E-3-0.905915954E-6i,
+0.599108986E-3-0.123533994E-5i,
+0.518838642E-3-0.105415677E-5i,
+0.331915246E-3+0.271774780E-6i,
+0.162484270E-3+0.357425029E-5i,
+0.508553421E-4+0.964594619E-5i,
-0.562439982E-5+0.181643882E-4i,
-0.247013941E-4+0.263359034E-4i,
-0.242255319E-4+0.268670992E-4i,
-0.166976788E-4+0.610463849E-5i,
-0.888209433E-5-0.552835227E-4i,
-0.329423983E-5-0.176591842E-3i,
-0.263539192E-6-0.360743987E-3i,
+0.922387187E-6-0.563883281E-3i,
+0.106429479E-5-0.651184935E-3i,
+0.822290701E-6-0.351541588E-3i,
+0.467566878E-6+0.752794149E-3i,
+0.210053159E-6+0.313399010E-2i,
+0.316887636E-7+0.702275708E-2i,
-0.351807508E-7+0.118032536E-1i,
-0.449268462E-7+0.150660956E-1i,
-0.673968046E-7+0.115134232E-1i,
-0.243363374E-7-0.763661135E-2i,
-0.160489648E-7-0.533953868E-1i,
+0.413388523E-8-0.133755907i,
+0.533866320E-7-0.241916195i,
+0.292106428E-7-0.336465567i,
+0.276342984E-7-0.316060245i
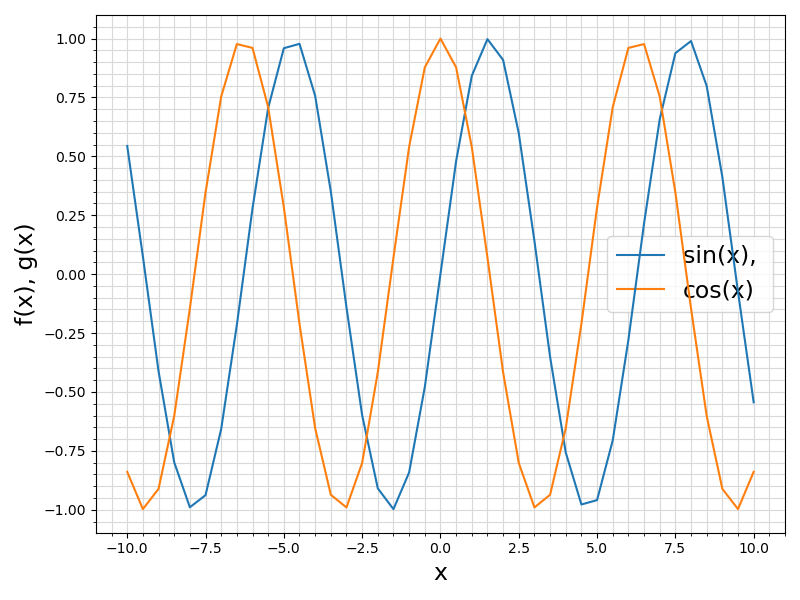
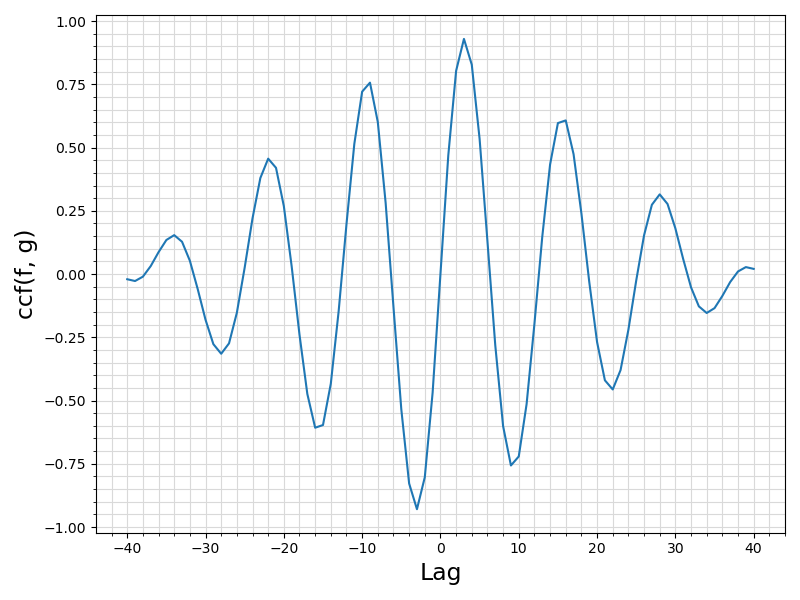
Postprocessing of the example output ⛓
3import matplotlib.pyplot
as plt
12for kind
in [
"sin.cos.RK"]:
14 file = glob.glob(
"*crd*"+kind+
".txt")[0]
15 df = pd.read_csv(file, delimiter =
",")
18 fig = plt.figure(figsize = (8, 6))
19 ax = plt.subplot(1,1,1)
20 ax.plot ( df.values[:, 0]
25 ax.set_xlabel(
"x", fontsize = 17)
26 ax.set_ylabel(
"f(x), g(x)", fontsize = 17)
27 ax.tick_params(axis =
"x", which =
"minor")
28 ax.tick_params(axis =
"y", which =
"minor")
29 plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
30 ax.legend([file.split(
".")[-4] +
"(x), ", file.split(
".")[-3] +
"(x)"], fontsize = fontsize)
32 plt.savefig(file.replace(
".txt",
".png"))
34 file = glob.glob(
"*ccf*"+kind+
".txt")[0]
35 df = pd.read_csv(file, delimiter =
",")
36 fig = plt.figure(figsize = (8, 6))
37 ax = plt.subplot(1,1,1)
38 ax.plot ( df.values[:, 0]
43 ax.set_xlabel(
"Lag", fontsize = 17)
44 ax.set_ylabel(
"ccf(f, g)", fontsize = 17)
45 ax.tick_params(axis =
"x", which =
"minor")
46 ax.tick_params(axis =
"y", which =
"minor")
47 plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
49 plt.savefig(file.replace(
".txt",
".png"))
Visualization of the example output ⛓
- Test:
- test_pm_sampleCCF
- Internal naming convention:
- The following illustrates the internal naming convention used for the procedures within this generic interface.
setCCF_FG_CK5()
||| || |||
||| || The type and kind parameters of the input sequences.
||| The input sequences `f` and `g`.
CCF: Cross-Correlation Function.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
-
If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
-
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
- Copyright
- Computational Data Science Lab
- Author:
- Fatemeh Bagheri, Monday 02:15 AM, September 27, 2021, Dallas, TX
Definition at line 784 of file pm_sampleCCF.F90.