pm_sampleCCF::getACF Interface Reference

Generate and return the auto-correlation function (ACF) \((f\star f)(\tau)\) of the discrete signal \(f\) lagging itself for a range of lags.
More...

Detailed Description

Generate and return the auto-correlation function (ACF) \((f\star f)(\tau)\) of the discrete signal \(f\) lagging itself for a range of lags.

This generic interface a flexible wrapper for the lower-level potentially faster generic interface setACF.
See the documentation of the parent module pm_sampleCCF for algorithmic details and auto-correlation definition.

Note

By default, the input sequence f is right-padded with zeros such that the resulting new sequence has the length max(lag(size(lag)), size(f) - 1) - min(lag(1), 1 - size(f)) + 1 before computing the auto-correlation.

Parameters

[in]	f	: The input contiguous vector of arbitrary size (of minimum 2) of, type complex of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128), type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), containing the first sequence in the auto-correlation computation.
[in]	lag	: The input vector of type integer of default kind IK of arbitrary size, containing the set of lags in ascending order for which the correlation must be computed. (optional. default = getRange(0, size(f) - 1))
[in]	norm	: The input scalar constant that can be: the constant nothing or an object of type nothing_type, implying that the input f must be used as is without any normalization. the constant meanshift or an object of type meanshift_type, implying that the input f must be mean-shifted before computing the auto-correlation. the constant stdscale or an object of type stdscale_type, implying that the input f must be scaled by a factor of 1 / sum(abs(f)**2). This option is particularly useful when the input sequence is already mean-shifted but not properly scaled. the constant zscore or an object of type zscore_type, implying that the input f must be mean-shifted and further scaled by a factor of 1 / sum(abs(f)**2). (optional, default = zscore.)

Returns

acf : The output allocatable vector of the same type and kind as the input f of size size(lag) containing the auto-correlation of the input f for the specified input lags.
Note that acf is always real-valued at lag 0 by definition, even when the input f is of type complex.
For all non-zero lags, the imaginary component of the auto-correlation function is an odd function.

Possible calling interfaces ⛓

use pm_sampleCCF, only: getACF
 
acf(1:size(lag)) = getACF(f(:), lag = lag, norm = norm)

Warning

The condition isAscending(lag) must hold for the corresponding input arguments.
This generic interface is merely a flexible wrapper around the generic subroutine interface setACF.
As such, all conditions and warnings associated with setACF equally apply to this generic interface.

Remarks

The procedures under discussion are impure.

See also

getACF
setACF
getCor
setCor
getRho
setRho
getCov
setCov
setECDF
getMean
setMean
getShifted
setShifted
getVar
setVar

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK, LK, RK
    use pm_io, only: getErrTableWrite
    use pm_io, only: display_type
    use pm_io, only: getFormat
    use pm_sampleCCF, only: getACF
    use pm_sampleCCF, only: getCCF
    use pm_arrayRange, only: getRange
    use pm_distUnif, only: getUnifRand
    use pm_distNorm, only: getNormLogPDF
    use pm_arrayPad, only: getPaddedr
    use pm_arrayFill, only: getFilled
    use pm_sampleShift, only: getShifted
    use pm_arrayResize, only: setResized
    use pm_arraySpace, only: getLinSpace
    use pm_sampleNorm, only: getNormed
    use pm_sampleMean, only: getMean
    use pm_sampleVar, only: getVar
 
    implicit none
 
    type(display_type) :: disp
    integer(IK) :: nsam, shift, itry, ntry = 1
    character(:), allocatable :: format
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!Compute the cross-correlation of two samples.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    block
        use pm_kind, only: TKG => RKS ! All other real types are also supported.
        integer(IK), allocatable :: lag(:)
        real(TKG), allocatable :: f(:), g(:)
        real(TKG), allocatable :: range(:), acf(:)
        call disp%skip()
        call disp%show("nsam = 41; shift = nsam")
                        nsam = 41; shift = nsam
        call disp%show("range = getLinSpace(-10., 10., nsam)")
                        range = getLinSpace(-10., 10., nsam)
        call disp%show("f = sin(range)")
                        f = sin(range)
        call disp%show("f")
        call disp%show( f )
        call disp%show("acf = getACF(f)")
                        acf = getACF(f)
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("g = f")
                        g = f
        call disp%show("acf = getCCF(f, g, lag = getRange(1 - nsam, nsam - 1_IK)) ! same as above.")
                        acf = getCCF(f, g, lag = getRange(1 - nsam, nsam - 1_IK)) ! same as above.
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("acf = getCCF(f, g, lag = getRange(0_IK, nsam - 1_IK)) ! same as above.")
                        acf = getCCF(f, g, lag = getRange(0_IK, nsam - 1_IK)) ! same as above.
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("lag = getRange(-nsam + 1_IK, nsam - 1_IK)")
                        lag = getRange(-nsam + 1_IK, nsam - 1_IK)
        call disp%show("acf = getACF(f, lag)")
                        acf = getACF(f, lag)
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("if (0 /= getErrTableWrite(SK_'getACF.crd.sin.RK.txt', reshape([range, f], [nsam, 2_IK]), header = SK_'crd,f')) error stop 'acf outputting failed.'")
                        if (0 /= getErrTableWrite(SK_'getACF.crd.sin.RK.txt', reshape([range, f], [nsam, 2_IK]), header = SK_'crd,f')) error stop 'acf outputting failed.'
        call disp%show("if (0 /= getErrTableWrite(SK_'getACF.acf.sin.RK.txt', reshape([real(lag, TKG), acf], [size(lag), 2]), header = SK_'lag,acf')) error stop 'acf outputting failed.'")
                        if (0 /= getErrTableWrite(SK_'getACF.acf.sin.RK.txt', reshape([real(lag, TKG), acf], [size(lag), 2]), header = SK_'lag,acf')) error stop 'acf outputting failed.'
        call disp%skip()
    end block
 
    block
        use pm_kind, only: TKG => RKS ! All other real types are also supported.
        integer(IK), allocatable :: lag(:)
        complex(TKG), allocatable :: f(:), g(:), acf(:), range(:)
        call disp%skip()
        call disp%show("nsam = 41; shift = nsam")
                        nsam = 41; shift = nsam
        call disp%show("range = getLinSpace((-10._TKG, +10._TKG), (+10._TKG, -10._TKG), nsam)")
                        range = getLinSpace((-10._TKG, +10._TKG), (+10._TKG, -10._TKG), nsam)
        call disp%show("f = sin(range)")
                        f = sin(range)
        call disp%show("f")
        call disp%show( f )
        call disp%show("acf = getACF(f)")
                        acf = getACF(f)
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("acf%re")
        call disp%show( acf%re )
        call disp%show("g = f")
                        g = f
        call disp%show("acf = getCCF(f, g, lag = getRange(0_IK, nsam - 1_IK)) ! same as above.")
                        acf = getCCF(f, g, lag = getRange(0_IK, nsam - 1_IK)) ! same as above.
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("acf%re")
        call disp%show( acf%re )
        call disp%show("lag = getRange(-nsam + 1_IK, nsam - 1_IK)")
                        lag = getRange(-nsam + 1_IK, nsam - 1_IK)
        call disp%show("acf = getACF(f, lag)")
                        acf = getACF(f, lag)
        call disp%show("size(acf)")
        call disp%show( size(acf) )
        call disp%show("acf")
        call disp%show( acf )
        call disp%show("acf%re")
        call disp%show( acf%re )
        call disp%skip()
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!Compute the cross-correlation of two samples.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
nsam = 41; shift = nsam
range = getLinSpace(-10., 10., nsam)
f = sin(range)
f
+0.544021070, +0.751511157E-1, -0.412118495, -0.798487127, -0.989358246, -0.937999964, -0.656986594, -0.215119988, +0.279415488, +0.705540299, +0.958924294, +0.977530122, +0.756802440, +0.350783229, -0.141120002, -0.598472178, -0.909297407, -0.997494996, -0.841470957, -0.479425550, +0.00000000, +0.479425550, +0.841470957, +0.997494996, +0.909297407, +0.598472178, +0.141120002, -0.350783229, -0.756802440, -0.977530122, -0.958924294, -0.705540299, -0.279415488, +0.215119988, +0.656986594, +0.937999964, +0.989358246, +0.798487127, +0.412118495, -0.751511157E-1, -0.544021130
acf = getACF(f)
size(acf)
+41
acf
+1.00000000, +0.852990508, +0.508950114, +0.610315278E-1, -0.377255470, -0.700775683, -0.837977588, -0.766536891, -0.516062975, -0.157883435, +0.214869067, +0.511390090, +0.665323377, +0.649478555, +0.479918420, +0.209043026, -0.899048448E-1, -0.342467040, -0.491509914, -0.510061145, -0.405582905, -0.215206355, +0.618809508E-2, +0.201431617, +0.325790167, +0.357164949, +0.299459368, +0.178786933, +0.341432206E-1, -0.944553539E-1, -0.176896036, -0.200005800, -0.169060707, -0.103816323, -0.306897387E-1, +0.262658000E-1, +0.527551509E-1, +0.478269048E-1, +0.227515157E-1, -0.420185737E-2, -0.152083794E-1
g = f
acf = getCCF(f, g, lag = getRange(1 - nsam, nsam - 1_IK)) ! same as above.
size(acf)
+81
acf
-0.152082434E-1, -0.420177961E-2, +0.227515455E-1, +0.478268564E-1, +0.527551807E-1, +0.262658577E-1, -0.306897387E-1, -0.103816353, -0.169060707, -0.200005770, -0.176895991, -0.944554210E-1, +0.341432393E-1, +0.178786933, +0.299459398, +0.357164949, +0.325790167, +0.201431692, +0.618788227E-2, -0.215206400, -0.405582935, -0.510061026, -0.491509914, -0.342467070, -0.899047554E-1, +0.209043026, +0.479918450, +0.649478555, +0.665323257, +0.511390150, +0.214869022, -0.157883465, -0.516063035, -0.766536891, -0.837977588, -0.700775623, -0.377255321, +0.610315837E-1, +0.508950174, +0.852990389, +1.00000000, +0.852990508, +0.508950114, +0.610315278E-1, -0.377255470, -0.700775683, -0.837977588, -0.766536891, -0.516062975, -0.157883435, +0.214869067, +0.511390090, +0.665323377, +0.649478555, +0.479918420, +0.209043026, -0.899048448E-1, -0.342467040, -0.491509914, -0.510061145, -0.405582905, -0.215206355, +0.618809508E-2, +0.201431617, +0.325790167, +0.357164949, +0.299459368, +0.178786933, +0.341432206E-1, -0.944553539E-1, -0.176896036, -0.200005800, -0.169060707, -0.103816323, -0.306897387E-1, +0.262658000E-1, +0.527551509E-1, +0.478269048E-1, +0.227515157E-1, -0.420185737E-2, -0.152083794E-1
acf = getCCF(f, g, lag = getRange(0_IK, nsam - 1_IK)) ! same as above.
size(acf)
+41
acf
+1.00000000, +0.852990508, +0.508950114, +0.610315278E-1, -0.377255470, -0.700775683, -0.837977588, -0.766536891, -0.516062975, -0.157883435, +0.214869067, +0.511390090, +0.665323377, +0.649478555, +0.479918420, +0.209043026, -0.899048448E-1, -0.342467040, -0.491509914, -0.510061145, -0.405582905, -0.215206355, +0.618809508E-2, +0.201431617, +0.325790167, +0.357164949, +0.299459368, +0.178786933, +0.341432206E-1, -0.944553539E-1, -0.176896036, -0.200005800, -0.169060707, -0.103816323, -0.306897387E-1, +0.262658000E-1, +0.527551509E-1, +0.478269048E-1, +0.227515157E-1, -0.420185737E-2, -0.152083794E-1
lag = getRange(-nsam + 1_IK, nsam - 1_IK)
acf = getACF(f, lag)
size(acf)
+81
acf
-0.152082434E-1, -0.420177961E-2, +0.227515455E-1, +0.478268564E-1, +0.527551807E-1, +0.262658577E-1, -0.306897387E-1, -0.103816353, -0.169060707, -0.200005770, -0.176895991, -0.944554210E-1, +0.341432393E-1, +0.178786933, +0.299459398, +0.357164949, +0.325790167, +0.201431692, +0.618788227E-2, -0.215206400, -0.405582935, -0.510061026, -0.491509914, -0.342467070, -0.899047554E-1, +0.209043026, +0.479918450, +0.649478555, +0.665323257, +0.511390150, +0.214869022, -0.157883465, -0.516063035, -0.766536891, -0.837977588, -0.700775623, -0.377255321, +0.610315837E-1, +0.508950174, +0.852990389, +1.00000000, +0.852990508, +0.508950114, +0.610315278E-1, -0.377255470, -0.700775683, -0.837977588, -0.766536891, -0.516062975, -0.157883435, +0.214869067, +0.511390090, +0.665323377, +0.649478555, +0.479918420, +0.209043026, -0.899048448E-1, -0.342467040, -0.491509914, -0.510061145, -0.405582905, -0.215206355, +0.618809508E-2, +0.201431617, +0.325790167, +0.357164949, +0.299459368, +0.178786933, +0.341432206E-1, -0.944553539E-1, -0.176896036, -0.200005800, -0.169060707, -0.103816323, -0.306897387E-1, +0.262658000E-1, +0.527551509E-1, +0.478269048E-1, +0.227515157E-1, -0.420185737E-2, -0.152083794E-1
if (0 /= getErrTableWrite(SK_'getACF.crd.sin.RK.txt', reshape([range, f], [nsam, 2_IK]), header = SK_'crd,f')) error stop 'acf outputting failed.'
if (0 /= getErrTableWrite(SK_'getACF.acf.sin.RK.txt', reshape([real(lag, TKG), acf], [size(lag), 2]), header = SK_'lag,acf')) error stop 'acf outputting failed.'
 
 
nsam = 41; shift = nsam
range = getLinSpace((-10._TKG, +10._TKG), (+10._TKG, -10._TKG), nsam)
f = sin(range)
f
(+5991.43115, -9240.88965), (+501.999237, -6660.97363), (-1669.71533, -3691.48242), (-1962.18994, -1479.37476), (-1474.61780, -216.864731), (-847.972107, +313.365570), (-360.236938, +413.376801), (-71.5428009, +324.783783), (+56.3624725, +193.678986), (+86.3214493, +86.7014389), (+71.1617279, +21.0486450), (+44.0026550, -9.48644638), (+20.6669369, -17.8378811), (+5.81346893, -15.4914541), (-1.42074847, -9.91762066), (-3.67000413, -4.84708261), (-3.42095494, -1.50930655), (-2.34651685, +0.150619254), (-1.29845750, +0.634963870), (-0.540612698, +0.457304120), (+0.00000000, +0.00000000), (+0.540612698, -0.457304120), (+1.29845750, -0.634963870), (+2.34651685, -0.150619254), (+3.42095494, +1.50930655), (+3.67000413, +4.84708261), (+1.42074847, +9.91762066), (-5.81346893, +15.4914541), (-20.6669369, +17.8378811), (-44.0026550, +9.48644638), (-71.1617279, -21.0486450), (-86.3214493, -86.7014389), (-56.3624725, -193.678986), (+71.5428009, -324.783783), (+360.236938, -413.376801), (+847.972107, -313.365570), (+1474.61780, +216.864731), (+1962.18994, +1479.37476), (+1669.71533, +3691.48242), (-501.999237, +6660.97363), (-5991.43115, +9240.88965)
acf = getACF(f)
size(acf)
+41
acf
(+1.00000000, +0.00000000), (+0.532280743, -0.724063076E-8), (+0.198766142, -0.639958264E-8), (+0.157836042E-1, -0.266178812E-7), (-0.563193597E-1, -0.326456089E-7), (-0.657618716E-1, -0.800109909E-10), (-0.492888130E-1, +0.163233782E-7), (-0.282785110E-1, +0.426677182E-8), (-0.119718434E-1, +0.125023716E-7), (-0.234168605E-2, +0.941287315E-8), (+0.191123993E-2, +0.893625263E-8), (+0.289596664E-2, +0.120566073E-7), (+0.237952033E-2, -0.863945804E-8), (+0.146735343E-2, +0.143593430E-7), (+0.686338462E-3, +0.336529560E-7), (+0.190695326E-3, +0.389712831E-7), (-0.485323944E-4, +0.424204316E-7), (-0.118897369E-3, +0.448930919E-7), (-0.102819416E-3, +0.348534819E-7), (-0.564900438E-4, +0.247550808E-11), (-0.117491136E-4, -0.529622080E-8), (+0.137586003E-4, -0.341829720E-8), (+0.618905369E-5, -0.964795444E-8), (-0.503967276E-4, -0.395892652E-8), (-0.171413732E-3, +0.127203030E-7), (-0.357021519E-3, -0.112389884E-7), (-0.561832683E-3, -0.341714945E-8), (-0.650348898E-3, +0.00000000), (-0.351429480E-3, +0.232185435E-7), (+0.752596592E-3, -0.235569364E-8), (+0.313374051E-2, -0.160475402E-7), (+0.702255825E-2, +0.135687781E-7), (+0.118031166E-1, +0.195890806E-7), (+0.150660472E-1, +0.274995067E-7), (+0.115134194E-1, +0.759400631E-8), (-0.763660157E-2, +0.906426934E-8), (-0.533953607E-1, -0.211997406E-7), (-0.133755893, -0.520020871E-8), (-0.241916195, -0.197824352E-7), (-0.336465597, -0.507333864E-8), (-0.316060305, -0.122585364E-7)
acf%re
+1.00000000, +0.532280743, +0.198766142, +0.157836042E-1, -0.563193597E-1, -0.657618716E-1, -0.492888130E-1, -0.282785110E-1, -0.119718434E-1, -0.234168605E-2, +0.191123993E-2, +0.289596664E-2, +0.237952033E-2, +0.146735343E-2, +0.686338462E-3, +0.190695326E-3, -0.485323944E-4, -0.118897369E-3, -0.102819416E-3, -0.564900438E-4, -0.117491136E-4, +0.137586003E-4, +0.618905369E-5, -0.503967276E-4, -0.171413732E-3, -0.357021519E-3, -0.561832683E-3, -0.650348898E-3, -0.351429480E-3, +0.752596592E-3, +0.313374051E-2, +0.702255825E-2, +0.118031166E-1, +0.150660472E-1, +0.115134194E-1, -0.763660157E-2, -0.533953607E-1, -0.133755893, -0.241916195, -0.336465597, -0.316060305
g = f
acf = getCCF(f, g, lag = getRange(0_IK, nsam - 1_IK)) ! same as above.
size(acf)
+41
acf
(+0.999999940, +0.00000000), (+0.532280743, -0.724063032E-8), (+0.198766112, -0.639958175E-8), (+0.157836024E-1, -0.266178777E-7), (-0.563193560E-1, -0.326456053E-7), (-0.657618642E-1, -0.800109839E-10), (-0.492888093E-1, +0.163233764E-7), (-0.282785092E-1, +0.426677138E-8), (-0.119718425E-1, +0.125023698E-7), (-0.234168582E-2, +0.941287226E-8), (+0.191123970E-2, +0.893625174E-8), (+0.289596641E-2, +0.120566055E-7), (+0.237952010E-2, -0.863945715E-8), (+0.146735332E-2, +0.143593413E-7), (+0.686338404E-3, +0.336529524E-7), (+0.190695311E-3, +0.389712760E-7), (-0.485323908E-4, +0.424204281E-7), (-0.118897355E-3, +0.448930884E-7), (-0.102819402E-3, +0.348534783E-7), (-0.564900365E-4, +0.247550786E-11), (-0.117491127E-4, -0.529622035E-8), (+0.137585985E-4, -0.341829676E-8), (+0.618905324E-5, -0.964795355E-8), (-0.503967240E-4, -0.395892608E-8), (-0.171413718E-3, +0.127203021E-7), (-0.357021490E-3, -0.112389875E-7), (-0.561832625E-3, -0.341714923E-8), (-0.650348840E-3, +0.00000000), (-0.351429451E-3, +0.232185418E-7), (+0.752596534E-3, -0.235569342E-8), (+0.313374028E-2, -0.160475384E-7), (+0.702255778E-2, +0.135687763E-7), (+0.118031157E-1, +0.195890788E-7), (+0.150660453E-1, +0.274995031E-7), (+0.115134176E-1, +0.759400542E-8), (-0.763660111E-2, +0.906426845E-8), (-0.533953533E-1, -0.211997389E-7), (-0.133755878, -0.520020782E-8), (-0.241916165, -0.197824317E-7), (-0.336465567, -0.507333819E-8), (-0.316060275, -0.122585355E-7)
acf%re
+0.999999940, +0.532280743, +0.198766112, +0.157836024E-1, -0.563193560E-1, -0.657618642E-1, -0.492888093E-1, -0.282785092E-1, -0.119718425E-1, -0.234168582E-2, +0.191123970E-2, +0.289596641E-2, +0.237952010E-2, +0.146735332E-2, +0.686338404E-3, +0.190695311E-3, -0.485323908E-4, -0.118897355E-3, -0.102819402E-3, -0.564900365E-4, -0.117491127E-4, +0.137585985E-4, +0.618905324E-5, -0.503967240E-4, -0.171413718E-3, -0.357021490E-3, -0.561832625E-3, -0.650348840E-3, -0.351429451E-3, +0.752596534E-3, +0.313374028E-2, +0.702255778E-2, +0.118031157E-1, +0.150660453E-1, +0.115134176E-1, -0.763660111E-2, -0.533953533E-1, -0.133755878, -0.241916165, -0.336465567, -0.316060275
lag = getRange(-nsam + 1_IK, nsam - 1_IK)
acf = getACF(f, lag)
size(acf)
+81
acf
(-0.316060305, -0.530768851E-7), (-0.336465597, -0.123534010E-7), (-0.241916209, +0.179410986E-8), (-0.133755907, -0.108240816E-8), (-0.533953607E-1, +0.164513967E-7), (-0.763660576E-2, +0.528450750E-8), (+0.115134027E-1, -0.128890791E-7), (+0.150660472E-1, -0.246229863E-7), (+0.118031232E-1, -0.649559562E-8), (+0.702256477E-2, -0.663351640E-8), (+0.313373981E-2, +0.322379479E-8), (+0.752626860E-3, -0.150611434E-7), (-0.351462484E-3, -0.642972182E-7), (-0.650348898E-3, +0.00000000), (-0.561832741E-3, -0.338393704E-7), (-0.357040699E-3, -0.166201719E-7), (-0.171417589E-3, -0.124814195E-7), (-0.504101117E-4, -0.782793919E-8), (+0.616589114E-5, -0.893987639E-8), (+0.137529387E-4, -0.102945008E-8), (-0.117722766E-4, +0.402788691E-8), (-0.565011105E-4, -0.876632811E-8), (-0.102823535E-3, -0.310065715E-7), (-0.118909717E-3, -0.163408875E-8), (-0.485323944E-4, -0.551795587E-8), (+0.190687104E-3, -0.122055788E-7), (+0.686321990E-3, +0.162704197E-7), (+0.146738638E-2, -0.315121040E-8), (+0.237947912E-2, +0.161755569E-7), (+0.289596664E-2, +0.892634944E-8), (+0.191128114E-2, +0.167481886E-7), (-0.234168814E-2, -0.851144044E-8), (-0.119718509E-1, -0.245817446E-7), (-0.282784998E-1, -0.378519189E-7), (-0.492888168E-1, -0.192738074E-7), (-0.657618865E-1, -0.189770137E-7), (-0.563193932E-1, -0.128433686E-8), (+0.157836135E-1, +0.268493370E-7), (+0.198766083, +0.419967705E-7), (+0.532280743, +0.106876527E-6), (+1.00000000, +0.00000000), (+0.532280743, -0.724063076E-8), (+0.198766142, -0.639958264E-8), (+0.157836042E-1, -0.266178812E-7), (-0.563193597E-1, -0.326456089E-7), (-0.657618716E-1, -0.800109909E-10), (-0.492888130E-1, +0.163233782E-7), (-0.282785110E-1, +0.426677182E-8), (-0.119718434E-1, +0.125023716E-7), (-0.234168605E-2, +0.941287315E-8), (+0.191123993E-2, +0.893625263E-8), (+0.289596664E-2, +0.120566073E-7), (+0.237952033E-2, -0.863945804E-8), (+0.146735343E-2, +0.143593430E-7), (+0.686338462E-3, +0.336529560E-7), (+0.190695326E-3, +0.389712831E-7), (-0.485323944E-4, +0.424204316E-7), (-0.118897369E-3, +0.448930919E-7), (-0.102819416E-3, +0.348534819E-7), (-0.564900438E-4, +0.247550808E-11), (-0.117491136E-4, -0.529622080E-8), (+0.137586003E-4, -0.341829720E-8), (+0.618905369E-5, -0.964795444E-8), (-0.503967276E-4, -0.395892652E-8), (-0.171413732E-3, +0.127203030E-7), (-0.357021519E-3, -0.112389884E-7), (-0.561832683E-3, -0.341714945E-8), (-0.650348898E-3, +0.00000000), (-0.351429480E-3, +0.232185435E-7), (+0.752596592E-3, -0.235569364E-8), (+0.313374051E-2, -0.160475402E-7), (+0.702255825E-2, +0.135687781E-7), (+0.118031166E-1, +0.195890806E-7), (+0.150660472E-1, +0.274995067E-7), (+0.115134194E-1, +0.759400631E-8), (-0.763660157E-2, +0.906426934E-8), (-0.533953607E-1, -0.211997406E-7), (-0.133755893, -0.520020871E-8), (-0.241916195, -0.197824352E-7), (-0.336465597, -0.507333864E-8), (-0.316060305, -0.122585364E-7)
acf%re
-0.316060305, -0.336465597, -0.241916209, -0.133755907, -0.533953607E-1, -0.763660576E-2, +0.115134027E-1, +0.150660472E-1, +0.118031232E-1, +0.702256477E-2, +0.313373981E-2, +0.752626860E-3, -0.351462484E-3, -0.650348898E-3, -0.561832741E-3, -0.357040699E-3, -0.171417589E-3, -0.504101117E-4, +0.616589114E-5, +0.137529387E-4, -0.117722766E-4, -0.565011105E-4, -0.102823535E-3, -0.118909717E-3, -0.485323944E-4, +0.190687104E-3, +0.686321990E-3, +0.146738638E-2, +0.237947912E-2, +0.289596664E-2, +0.191128114E-2, -0.234168814E-2, -0.119718509E-1, -0.282784998E-1, -0.492888168E-1, -0.657618865E-1, -0.563193932E-1, +0.157836135E-1, +0.198766083, +0.532280743, +1.00000000, +0.532280743, +0.198766142, +0.157836042E-1, -0.563193597E-1, -0.657618716E-1, -0.492888130E-1, -0.282785110E-1, -0.119718434E-1, -0.234168605E-2, +0.191123993E-2, +0.289596664E-2, +0.237952033E-2, +0.146735343E-2, +0.686338462E-3, +0.190695326E-3, -0.485323944E-4, -0.118897369E-3, -0.102819416E-3, -0.564900438E-4, -0.117491136E-4, +0.137586003E-4, +0.618905369E-5, -0.503967276E-4, -0.171413732E-3, -0.357021519E-3, -0.561832683E-3, -0.650348898E-3, -0.351429480E-3, +0.752596592E-3, +0.313374051E-2, +0.702255825E-2, +0.118031166E-1, +0.150660472E-1, +0.115134194E-1, -0.763660157E-2, -0.533953607E-1, -0.133755893, -0.241916195, -0.336465597, -0.316060305
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
linewidth = 2
fontsize = 17
 
for kind in ["sin.RK"]:
 
    file = glob.glob("*crd*"+kind+".txt")[0]
    df = pd.read_csv(file, delimiter = ",")
 
    #print(df.values)
    fig = plt.figure(figsize = (8, 6))
    ax = plt.subplot(1,1,1)
    ax.plot ( df.values[:, 0]
            , df.values[:, 1]
            , zorder = 1000
            )
    plt.minorticks_on()
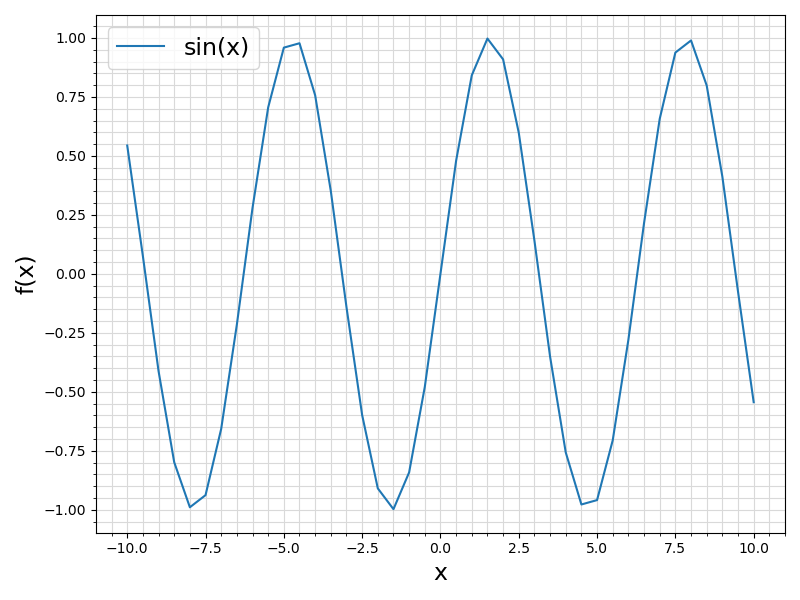
    ax.set_xlabel("x", fontsize = 17)
    ax.set_ylabel("f(x)", fontsize = 17)
    ax.tick_params(axis = "x", which = "minor")
    ax.tick_params(axis = "y", which = "minor")
    plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
    ax.legend([file.split(".")[-3] + "(x)"], fontsize = fontsize)
    plt.tight_layout()
    plt.savefig(file.replace(".txt",".png"))
 
    file = glob.glob("*acf*"+kind+".txt")[0]
    df = pd.read_csv(file, delimiter = ",")
    fig = plt.figure(figsize = (8, 6))
    ax = plt.subplot(1,1,1)
    ax.plot ( df.values[:, 0]
            , df.values[:, 1]
            , zorder = 1000
            )
    plt.minorticks_on()
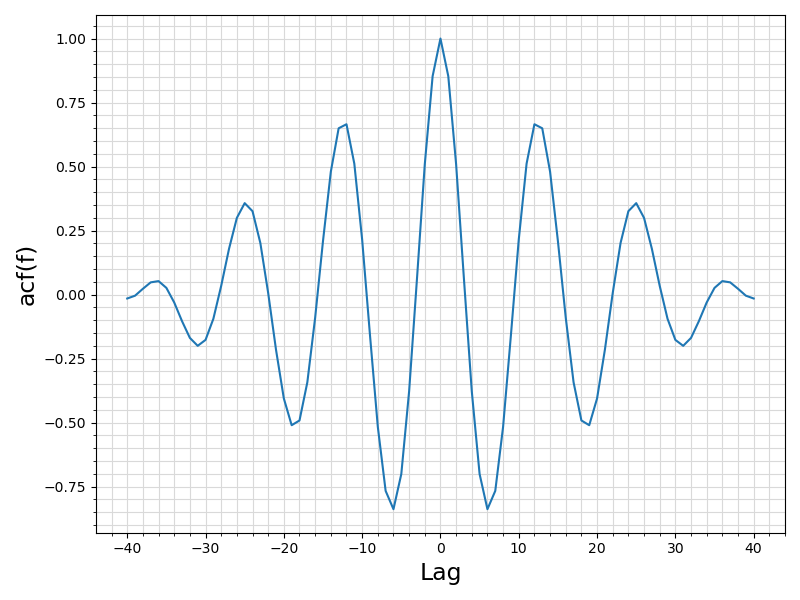
    ax.set_xlabel("Lag", fontsize = 17)
    ax.set_ylabel("acf(f)", fontsize = 17)
    ax.tick_params(axis = "x", which = "minor")
    ax.tick_params(axis = "y", which = "minor")
    plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
    plt.tight_layout()
    plt.savefig(file.replace(".txt",".png"))

Visualization of the example output ⛓

Test:

test_pm_sampleCCF

Internal naming convention:

The following illustrates the internal naming convention used for the procedures within this generic interface.

getACF_D1_CK5()
   ||| || |||
   ||| || The type and kind parameters of the input sequence.
   ||| The dimension of the input sequence `f`.
   ACF: Cross-Correlation Function.

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Fatemeh Bagheri, Monday 02:15 AM, September 27, 2021, Dallas, TX

Definition at line 264 of file pm_sampleCCF.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_sampleCCF.F90