Return the (weighted) mean of a pair of time series or of an input sample of nsam observations with ndim = 1 or 2 attributes, optionally weighted by the input weight, optionally also sum(weight) and optionally, sum(weight**2).
More...

Detailed Description

Return the (weighted) mean of a pair of time series or of an input sample of nsam observations with ndim = 1 or 2 attributes, optionally weighted by the input weight, optionally also sum(weight) and optionally, sum(weight**2).

This generic interface is developed to specifically improve the performance of other procedures where sum(weight) or sum(weight**2) are also needed in addition to the mean of the weighted sample.
For example, this situation occurs frequently in the computation of the variance or covariance matrix of a weighted sample.

Parameters

[out]	mean	: The output object of, type `complex` of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128), type `real` of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), containing the data mean. When the input `sample` has the shape `(nsam)`, the output mean must be a scalar. When the input `x` and `y` are present, the output `mean` must be of shape `mean(1:2)`. When the input `sample` has the shape `(nsam, ndim)` or `(ndim, nsam)`, the output mean must be a vector of length `ndim`.
[in]	x	: The `contiguous` array of shape `(nsam)` of the same type and kind as the output `mean`, containing the first of the two data series whose `mean` is to be computed. (optional. It must be present if and only if* the input argument `sample` is missing and `y` is present.)
[in]	y	: The `contiguous` of the same type and kind and shape as the input `x`, containing the second of the two data series whose `mean` is to be computed. (optional. It must be present if and only if* the input argument `sample` is missing and `x` is present.)
[in]	sample	: The `contiguous` array of shape `(nsam)`, `(ndim, nsam)` or `(nsam, ndim)` of the same type and kind as the output `mean`, containing the sample whose `mean` is to be computed. (optional. It must be present if and only if* the input arguments `x` and `y` are missing.)
[in]	dim	: The input scalar `integer` of default kind IK representing the dimension (`1` or `2`) of the input `sample` along which the mean must be computed. If `dim = 1`, the input `sample` of rank `2` is assumed to have the shape `(nsam, ndim)`. If `dim = 2`, the input `sample` of rank `2` is assumed to have the shape `(ndim, nsam)`. The input `dim` must always be `1` or missing for an input `sample` of rank `1`. (optional. It can be present only if `sample` is also present. If missing, the mean of the whole input `sample` is computed.)
[in]	weight	: The `contiguous` vector of length `nsam` of type `integer` of default kind IK, or type `real` of the same kind as that of the output `mean`, containing the corresponding weights of the data points in the input `sample` or the input pair `x` and `y`.
[out]	weisum	: The output scalar of the same type and kind as the input `weight`. On output, it will contain `sum(weight)`. This quantity is frequently needed in computing the weighted sample variance. (optional. It must be present if and only if the input argument `weight` is also present.)

Possible calling interfaces ⛓

: use pm_sampleMean, only: setMean

! XY sample.

call setMean(mean(1:2), x(1 : nsam), y(1 : nsam))

call setMean(mean(1:2), x(1 : nsam), y(1 : nsam), weight(1 : nsam), weisum)

! 1D sample.

call setMean(mean, sample(1 : nsam))

call setMean(mean, sample(1 : nsam), weight(1 : nsam), weisum)

call setMean(mean, sample(1 : nsam), dim)

call setMean(mean, sample(1 : nsam), dim, weight(1 : nsam), weisum)

! 2D sample.

call setMean(mean(1 : ndim), sample(:,:))

call setMean(mean(1 : ndim), sample(:,:), weight(1 : nsam), weisum)

call setMean(mean(1 : ndim), sample(:,:), dim)

call setMean(mean(1 : ndim), sample(:,:), dim, weight(1 : nsam), weisum)

pm_sampleMean::setMean
Return the (weighted) mean of a pair of time series or of an input sample of nsam observations with n...
Definition: pm_sampleMean.F90:2008

pm_sampleMean
This module contains classes and procedures for computing the first moment (i.e., the statistical mea...
Definition: pm_sampleMean.F90:104

Warning: The condition all(0. <= weight) must hold for the corresponding input arguments.
The condition 1 <= dim .and. dim <= rank(sample) must hold for the corresponding input arguments.
The condition size(sample, dim) == size(weight, 1) must hold for the corresponding input arguments.
The condition (dim == 1 .and. size(mean, 1) == size(sample, 2)) .or. (dim == 2 .and. size(mean, 1) == size(sample, 1)) must hold for the corresponding input arguments.
The condition size(x) == size(weight) must hold for the corresponding input arguments.
The condition size(x) == size(y) must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.; The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

Note

If the input sample is to be an array of type integer, simply convert the sample to an array of type real of the desired kind for the output real mean of the sample.
There is no point in accepting an input sample of type integer since it will be inevitably converted to an array of type real within the procedure to avoid potential integer overflow.
Furthermore, an sample of type integer creates ambiguity about the kind of the real-valued returned mean by the procedure.
See the notes in the description of the pm_sampleMean.

Note that the mean of any one or two-dimensional sample can be simply computed via the Fortran intrinsic routine sum():

integer                         :: i
integer , parameter             :: NDIM = 3_IK
integer , parameter             :: NSAM = 1000_IK
real    , parameter             :: sample(NDIM,NSAM) = reshape([( real(i,RK), i = 1, NSAM )], shape = shape(sample))
real    , allocatable   :: mean(:)
mean = sum(sample, dim = 1) / size(transpose(sample), dim = 1)  ! assuming the first dimension represents the observations.
mean = sum(sample, dim = 2) / size(sample, dim = 2)             ! assuming the second dimension represents the observations.

The mean of a whole multidimensional array can be obtained by either,

reshaping the array to a vector form and passing it to this procedure, or
mapping the array to a 1-dimensional pointer array of the same size as the ndim dimensional array.

See the examples below.

Developer Remark:: The logic behind allowing a pair of time series data x and y is to allow fast computation of the mean of the pair and the weight sums in one loop.
This pattern occurs frequently in the computation of correlation coefficients.

See also: getVar
getMean
setVarMean

Example usage ⛓

: 1program example

2

3 use pm_kind, only: SK, IK

4 use pm_kind, only: TKG => RKS ! All other real types are also supported.

5 use pm_arrayResize, only: setResized

6 use pm_distUnif, only: getUnifRand

7 use pm_sampleMean, only: setMean

8 use pm_io, only: display_type

9

10 implicit none

11

12 integer(IK) :: idim, ndim, nsam

13 type(display_type) :: disp

14 disp = display_type(file = "main.out.F90")

15

16 call disp%skip()

17 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

18 call disp%show("!Compute the mean of a 1-D array.")

19 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

20 call disp%skip()

21

22 block

23 real(TKG) :: mean

24 real(TKG), allocatable :: sample(:)

25 call disp%skip()

26 call disp%show("nsam = getUnifRand(1, 5)")

27 nsam = getUnifRand(1, 5)

28 call disp%show("sample = getUnifRand(0., 1., nsam)")

29 sample = getUnifRand(0., 1., nsam)

30 call disp%show("sample")

31 call disp%show( sample )

32 call disp%show("call setMean(mean, sample)")

33 call setMean(mean, sample)

34 call disp%show("mean")

35 call disp%show( mean )

36 call disp%show("call setMean(mean, sample, dim = 1_IK)")

37 call setMean(mean, sample, dim = 1_IK)

38 call disp%show("mean")

39 call disp%show( mean )

40 call disp%skip()

41 end block

42

43 call disp%skip()

44 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

45 call disp%show("!Compute the mean of a pair of data series.")

46 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

47 call disp%skip()

48

49 block

50 real(TKG) :: mean(2)

51 real(TKG), allocatable :: sample(:,:)

52 real(TKG), allocatable :: weight(:)

53 real(TKG) :: weisum

54 call disp%skip()

55 call disp%show("nsam = getUnifRand(1, 5)")

56 nsam = getUnifRand(1, 5)

57 call disp%show("sample = getUnifRand(0., 1., nsam, 2_IK)")

58 sample = getUnifRand(0., 1., nsam, 2_IK)

59 call disp%show("sample")

60 call disp%show( sample )

61 call disp%show("call setMean(mean, sample(:,1), sample(:,2))")

62 call setMean(mean, sample(:,1), sample(:,2))

63 call disp%show("mean")

64 call disp%show( mean )

65 call disp%show("call setMean(mean, sample, dim = 1_IK) ! for comparison.")

66 call setMean(mean, sample, dim = 1_IK) ! for comparison.

67 call disp%show("mean")

68 call disp%show( mean )

69 call disp%skip()

70 call disp%show("weight = getUnifRand(1, 100, nsam)")

71 weight = getUnifRand(1, 100, nsam)

72 call disp%show("weight")

73 call disp%show( weight )

74 call disp%show("call setMean(mean, sample(:,1), sample(:,2), weight, weisum)")

75 call setMean(mean, sample(:,1), sample(:,2), weight, weisum)

76 call disp%show("weisum")

77 call disp%show( weisum )

78 call disp%show("mean")

79 call disp%show( mean )

80 call disp%show("call setMean(mean, sample, 1_IK, weight, weisum) ! for comparison.")

81 call setMean(mean, sample, 1_IK, weight, weisum) ! for comparison.

82 call disp%show("weisum")

83 call disp%show( weisum )

84 call disp%show("mean")

85 call disp%show( mean )

86 call disp%skip()

87 call disp%show("call setMean(mean, sample(:,1), sample(:,2), weight, weisum)")

88 call setMean(mean, sample(:,1), sample(:,2), weight, weisum)

89 call disp%show("weisum")

90 call disp%show( weisum )

91 call disp%show("mean")

92 call disp%show( mean )

93 call disp%show("call setMean(mean, sample, 1_IK, weight, weisum) ! for comparison.")

94 call setMean(mean, sample, 1_IK, weight, weisum) ! for comparison.

95 call disp%show("weisum")

96 call disp%show( weisum )

97 call disp%show("mean")

98 call disp%show( mean )

99 call disp%skip()

100 end block

101

102 call disp%skip()

103 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

104 call disp%show("!Compute the mean of a 2-D array along a specific dimension.")

105 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

106 call disp%skip()

107

108 block

109 real(TKG), allocatable :: mean(:)

110 real(TKG), allocatable :: sample(:,:)

111 call disp%skip()

112 call disp%show("ndim = getUnifRand(1, 3); nsam = getUnifRand(1, 5)")

113 ndim = getUnifRand(1, 3); nsam = getUnifRand(1, 5)

114 call disp%show("sample = getUnifRand(0., 1., ndim, nsam)")

115 sample = getUnifRand(0., 1., ndim, nsam)

116 call disp%show("sample")

117 call disp%show( sample )

118 call disp%show("call setResized(mean, ndim)")

119 call setResized(mean, ndim)

120 call disp%show("call setMean(mean(1), sample)")

121 call setMean(mean(1), sample)

122 call disp%show("mean(1)")

123 call disp%show( mean(1) )

124 call disp%show("call setMean(mean, sample, dim = 2_IK)")

125 call setMean(mean, sample, dim = 2_IK)

126 call disp%show("mean")

127 call disp%show( mean )

128 call disp%show("call setMean(mean, transpose(sample), dim = 1_IK)")

129 call setMean(mean, transpose(sample), dim = 1_IK)

130 call disp%show("mean")

131 call disp%show( mean )

132 call disp%skip()

133 end block

134

135 call disp%skip()

136 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

137 call disp%show("!Compute the mean of a 1-D weighted array.")

138 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

139 call disp%skip()

140

141 block

142 real(TKG) :: mean

143 real(TKG), allocatable :: sample(:)

144 real(TKG), allocatable :: weight(:)

145 real(TKG) :: weisum

146 call disp%skip()

147 call disp%show("nsam = getUnifRand(1, 5)")

148 nsam = getUnifRand(1, 5)

149 call disp%show("sample = getUnifRand(0., 1., nsam)")

150 sample = getUnifRand(0., 1., nsam)

151 call disp%show("sample")

152 call disp%show( sample )

153 call disp%show("weight = getUnifRand(1, 100, nsam)")

154 weight = getUnifRand(1, 100, nsam)

155 call disp%show("weight")

156 call disp%show( weight )

157 call disp%show("call setMean(mean, sample)")

158 call setMean(mean, sample)

159 call disp%show("mean")

160 call disp%show( mean )

161 call disp%show("call setMean(mean, sample, dim = 1_IK)")

162 call setMean(mean, sample, dim = 1_IK)

163 call disp%show("mean")

164 call disp%show( mean )

165 call disp%show("call setMean(mean, sample, weight, weisum)")

166 call setMean(mean, sample, weight, weisum)

167 call disp%show("[weisum, sum(weight)]")

168 call disp%show( [weisum, sum(weight)] )

169 call disp%show("mean")

170 call disp%show( mean )

171 call disp%show("call setMean(mean, sample, 1_IK, weight, weisum)")

172 call setMean(mean, sample, 1_IK, weight, weisum)

173 call disp%show("[weisum, sum(weight)]")

174 call disp%show( [weisum, sum(weight)] )

175 call disp%show("mean")

176 call disp%show( mean )

177 call disp%skip()

178 end block

179

180 call disp%skip()

181 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

182 call disp%show("!Compute the mean of a 2-D weighted array along a specific dimension.")

183 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

184 call disp%skip()

185

186 block

187 real(TKG), allocatable :: mean(:)

188 real(TKG), allocatable :: sample(:,:)

189 real(TKG), allocatable :: weight(:)

190 real(TKG) :: weisum

191 call disp%skip()

192 call disp%show("ndim = getUnifRand(1, 3); nsam = getUnifRand(1, 5)")

193 ndim = getUnifRand(1, 3); nsam = getUnifRand(1, 5)

194 call disp%show("sample = getUnifRand(0., 1., ndim, nsam)")

195 sample = getUnifRand(0., 1., ndim, nsam)

196 call disp%show("sample")

197 call disp%show( sample )

198 call disp%show("weight = getUnifRand(1, 100, nsam)")

199 weight = getUnifRand(1, 100, nsam)

200 call disp%show("weight")

201 call disp%show( weight )

202 call disp%show("call setResized(mean, ndim)")

203 call setResized(mean, ndim)

204 call disp%show("call setMean(mean(1), sample, [(weight, idim = 1, ndim)], weisum)")

205 call setMean(mean(1), sample, [(weight, idim = 1, ndim)], weisum)

206 call disp%show("mean(1)")

207 call disp%show( mean(1) )

208 call disp%show("call setMean(mean, sample, 2_IK, weight, weisum)")

209 call setMean(mean, sample, 2_IK, weight, weisum)

210 call disp%show("[weisum, sum(weight)]")

211 call disp%show( [weisum, sum(weight)] )

212 call disp%show("mean")

213 call disp%show( mean )

214 call disp%show("call setMean(mean, transpose(sample), 1_IK, weight, weisum)")

215 call setMean(mean, transpose(sample), 1_IK, weight, weisum)

216 call disp%show("[weisum, sum(weight)]")

217 call disp%show( [weisum, sum(weight)] )

218 call disp%show("mean")

219 call disp%show( mean )

220 call disp%skip()

221 end block

222

223 call disp%skip()

224 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

225 call disp%show("!Compute the mean of a multidimensional array by associating it with a 1D pointer.")

226 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

227 call disp%skip()

228

229 block

230 real(TKG) :: mean

231 integer(IK) :: nslice

232 real(TKG), allocatable, target :: sample(:,:,:)

233 real(TKG), pointer :: samptr(:)

234 call disp%skip()

235 call disp%show("ndim = getUnifRand(1, 2); nsam = getUnifRand(1, 3); nslice = getUnifRand(1, 4)")

236 ndim = getUnifRand(1, 2); nsam = getUnifRand(1, 3); nslice = getUnifRand(1, 4)

237 call disp%show("sample = getUnifRand(0., 1., ndim, nsam, nslice)")

238 sample = getUnifRand(0., 1., ndim, nsam, nslice)

239 call disp%show("sample")

240 call disp%show( sample )

241 call disp%show("shape(sample)")

242 call disp%show( shape(sample) )

243 call disp%show("samptr(1:product(shape(sample))) => sample")

244 samptr(1:product(shape(sample))) => sample

245 call disp%show("call setMean(mean, samptr)")

246 call setMean(mean, samptr)

247 call disp%show("nullify(samptr)")

248 nullify(samptr)

249 call disp%show("mean")

250 call disp%show( mean )

251 call disp%show("call setMean(mean, reshape(sample, [product(shape(sample))]))")

252 call setMean(mean, reshape(sample, [product(shape(sample))]))

253 call disp%show("mean")

254 call disp%show( mean )

255 call disp%skip()

256 end block

257

258end program example

pm_arrayResize::setResized
Allocate or resize (shrink or expand) an input allocatable scalar string or array of rank 1....
Definition: pm_arrayResize.F90:249

pm_distUnif::getUnifRand
Generate and return a scalar or a contiguous array of rank 1 of length s1 of randomly uniformly distr...
Definition: pm_distUnif.F90:4150

pm_io::show
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11726

pm_io::skip
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11508

pm_arrayResize
This module contains procedures and generic interfaces for resizing allocatable arrays of various typ...
Definition: pm_arrayResize.F90:81

pm_distUnif
This module contains classes and procedures for computing various statistical quantities related to t...
Definition: pm_distUnif.F90:274

pm_io
This module contains classes and procedures for input/output (IO) or generic display operations on st...
Definition: pm_io.F90:252

pm_io::disp
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
Definition: pm_io.F90:11393

pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268

pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540

pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539

pm_kind::RKS
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Definition: pm_kind.F90:567

pm_io::display_type
Generate and return an object of type display_type.
Definition: pm_io.F90:10282

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe

2set PATH=..\..\..\lib;%PATH%

3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe

4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example output ⛓
1

2!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

3!Compute the mean of a 1-D array.

4!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

5

6

7nsam = getUnifRand(1, 5)

8sample = getUnifRand(0., 1., nsam)

9sample

10+0.920615017, +0.365559101, +0.128899038

11call setMean(mean, sample)

12mean

13+0.471691042

14call setMean(mean, sample, dim = 1_IK)

15mean

16+0.471691042

17

18

19!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

20!Compute the mean of a pair of data series.

21!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

22

23

24nsam = getUnifRand(1, 5)

25sample = getUnifRand(0., 1., nsam, 2_IK)

26sample

27+0.525721192, +0.377225876E-1

28+0.853543103, +0.610126376

29+0.344640970, +0.563148737

30+0.723670125E-1, +0.569932044

31call setMean(mean, sample(:,1), sample(:,2))

32mean

33+0.449068069, +0.445232451

34call setMean(mean, sample, dim = 1_IK) ! for comparison.

35mean

36+0.449068069, +0.445232451

37

38weight = getUnifRand(1, 100, nsam)

39weight

40+34.0000000, +90.0000000, +37.0000000, +11.0000000

41call setMean(mean, sample(:,1), sample(:,2), weight, weisum)

42weisum

43+172.000000

44mean

45+0.629308999, +0.484300524

46call setMean(mean, sample, 1_IK, weight, weisum) ! for comparison.

47weisum

48+172.000000

49mean

50+0.629308999, +0.484300524

51

52call setMean(mean, sample(:,1), sample(:,2), weight, weisum)

53weisum

54+172.000000

55mean

56+0.629308999, +0.484300524

57call setMean(mean, sample, 1_IK, weight, weisum) ! for comparison.

58weisum

59+172.000000

60mean

61+0.629308999, +0.484300524

62

63

64!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

65!Compute the mean of a 2-D array along a specific dimension.

66!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

67

68

69ndim = getUnifRand(1, 3); nsam = getUnifRand(1, 5)

70sample = getUnifRand(0., 1., ndim, nsam)

71sample

72+0.396403670E-1

73+0.439142227

74call setResized(mean, ndim)

75call setMean(mean(1), sample)

76mean(1)

77+0.239391297

78call setMean(mean, sample, dim = 2_IK)

79mean

80+0.396403670E-1, +0.439142227

81call setMean(mean, transpose(sample), dim = 1_IK)

82mean

83+0.396403670E-1, +0.439142227

84

85

86!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

87!Compute the mean of a 1-D weighted array.

88!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

89

90

91nsam = getUnifRand(1, 5)

92sample = getUnifRand(0., 1., nsam)

93sample

94+0.412422180, +0.752122641, +0.506295502

95weight = getUnifRand(1, 100, nsam)

96weight

97+49.0000000, +52.0000000, +40.0000000

98call setMean(mean, sample)

99mean

100+0.556946754

101call setMean(mean, sample, dim = 1_IK)

102mean

103+0.556946754

104call setMean(mean, sample, weight, weisum)

105[weisum, sum(weight)]

106+141.000000, +141.000000

107mean

108+0.564332545

109call setMean(mean, sample, 1_IK, weight, weisum)

110[weisum, sum(weight)]

111+141.000000, +141.000000

112mean

113+0.564332545

114

115

116!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

117!Compute the mean of a 2-D weighted array along a specific dimension.

118!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

119

120

121ndim = getUnifRand(1, 3); nsam = getUnifRand(1, 5)

122sample = getUnifRand(0., 1., ndim, nsam)

123sample

124+0.821849883, +0.541934490, +0.616343617E-1, +0.112378180

125+0.156146526, +0.739428580, +0.902320385, +0.950516701

126+0.896420479, +0.275964320, +0.159999073, +0.174723268

127weight = getUnifRand(1, 100, nsam)

128weight

129+46.0000000, +60.0000000, +77.0000000, +84.0000000

130call setResized(mean, ndim)

131call setMean(mean(1), sample, [(weight, idim = 1, ndim)], weisum)

132mean(1)

133+0.492886752

134call setMean(mean, sample, 2_IK, weight, weisum)

135[weisum, sum(weight)]

136+267.000000, +267.000000

137mean

138+0.316504806, +0.752324045, +0.317565113

139call setMean(mean, transpose(sample), 1_IK, weight, weisum)

140[weisum, sum(weight)]

141+267.000000, +267.000000

142mean

143+0.316504806, +0.752324045, +0.317565113

144

145

146!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

147!Compute the mean of a multidimensional array by associating it with a 1D pointer.

148!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

149

150

151ndim = getUnifRand(1, 2); nsam = getUnifRand(1, 3); nslice = getUnifRand(1, 4)

152sample = getUnifRand(0., 1., ndim, nsam, nslice)

153sample

154slice(:,:,1) =

155+0.634807169, +0.216954470

156shape(sample)

157+1, +2, +1

158samptr(1:product(shape(sample))) => sample

159call setMean(mean, samptr)

160nullify(samptr)

161mean

162+0.425880820

163call setMean(mean, reshape(sample, [product(shape(sample))]))

164mean

165+0.425880820

166

167

Benchmarks:

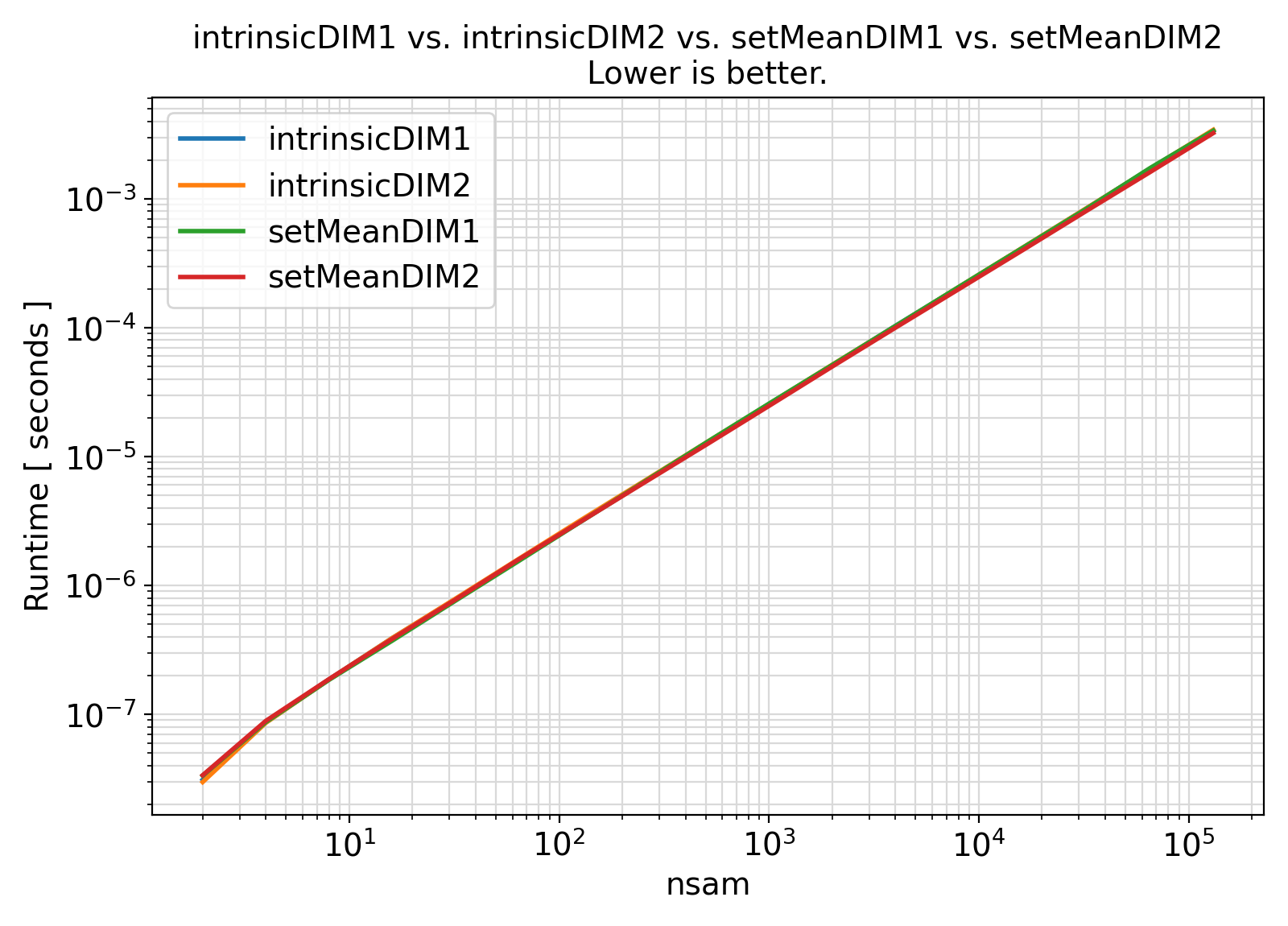
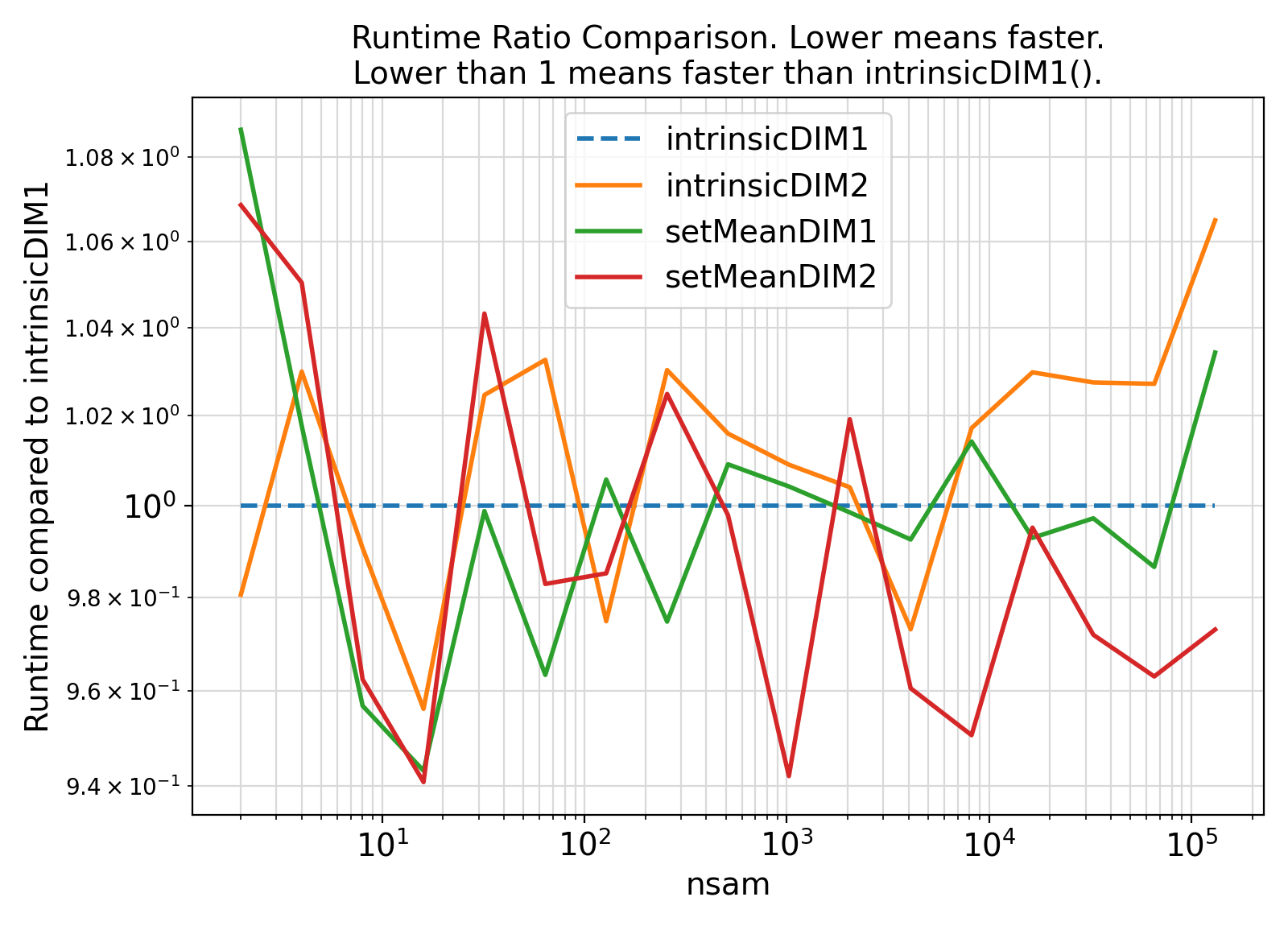
Benchmark :: The runtime performance of setMean along different sample dimensions. ⛓

! Test the performance of Cholesky factorization computation using an assumed-shape interface vs. explicit-shape interface.
program benchmark
 
    use pm_kind, only: IK, LK, RKG => RKD, SK
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: itry, ntry
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK)     , parameter         :: NARR = 18_IK
    real(RKG)       , allocatable       :: samdim1(:,:)
    real(RKG)       , allocatable       :: samdim2(:,:)
    type(bench_type), allocatable       :: bench(:)
    integer(IK)     , parameter         :: nsammax = 2**NARR
    integer(IK)     , parameter         :: ndim = 5_IK
    real(RKG)                           :: mean(ndim)
    integer(IK)                         :: isam, nsam
    real(RKG)                           :: dumm
 
    bench = [ bench_type(name = SK_"intrinsicDIM1", exec = intrinsicDIM1, overhead = setOverhead) &
            , bench_type(name = SK_"intrinsicDIM2", exec = intrinsicDIM2, overhead = setOverhead) &
            , bench_type(name = SK_"setMeanDIM1", exec = setMeanDIM1, overhead = setOverhead) &
            , bench_type(name = SK_"setMeanDIM2", exec = setMeanDIM2, overhead = setOverhead) &
            ]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "sample mean benchmarking..."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "nsam", (bench(i)%name, i = 1, size(bench))
 
        dumm = 0._RKG
        loopOverMatrixSize: do iarr = 1, NARR - 1
 
            nsam = 2**iarr
            ntry = nsammax / nsam
            allocate(samdim1(nsam, ndim), samdim2(ndim, nsam))
            write(*,"(*(g0,:,' '))") "Benchmarking setMeanDIM1() vs. setMeanDIM2()", nsam, ntry
 
            do i = 1, size(bench)
                bench(i)%timing = bench(i)%getTiming()
            end do
 
            write(fileUnit,"(*(g0,:,','))") nsam, (bench(i)%timing%mean / ntry, i = 1, size(bench))
            deallocate(samdim1, samdim2)
 
        end do loopOverMatrixSize
        write(*,"(*(g0,:,' '))") dumm
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        do itry = 1, ntry
            call random_number(mean)
            dumm = dumm - mean(1)
        end do
    end subroutine
 
    subroutine setSamDIM1()
        do isam = 1, nsam
            call random_number(samdim1(isam, 1 : ndim))
        end do
    end subroutine
 
    subroutine setSamDIM2()
        do isam = 1, nsam
            call random_number(samdim2(1 : ndim, isam))
        end do
    end subroutine
 
    subroutine setMeanDIM1()
        use pm_sampleMean, only: setMean
        do itry = 1, ntry
            call setSamDIM1()
            call setMean(mean, samdim1, dim = 1_IK)
            dumm = dumm + mean(1)
        end do
    end subroutine
 
    subroutine setMeanDIM2()
        use pm_sampleMean, only: setMean
        do itry = 1, ntry
            call setSamDIM2()
            call setMean(mean, samdim2, dim = 2_IK)
            dumm = dumm + mean(1)
        end do
    end subroutine
 
    subroutine intrinsicDIM1()
        do itry = 1, ntry
            call setSamDIM1()
            mean = sum(samdim1, dim = 1) / size(samdim1, dim = 1)
            dumm = dumm + mean(1)
        end do
    end subroutine
 
    subroutine intrinsicDIM2()
        do itry = 1, ntry
            call setSamDIM2()
            mean = sum(samdim2, dim = 2) / size(samdim1, dim = 2)
            dumm = dumm + mean(1)
        end do
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ",")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The procedures under the generic interface setMean can compute the covariance under two different sample axes.
Recall that C is a row-major language while Fortran is a column-major language.
As such, one would expect the computations for a sample whose observations are stored along the second axis would be faster in the Fortran programming language.
However, such an expectation does not appear to hold at all times and appears to depend significantly on the computing architecture and the number of data attributes involved.
The higher the number of data attributes, the more likely the computations along the second axis of sample will be faster.
Note that for small number of data attributes, the computations along the second data axis involve a small loop that has significant computational cost due to the implicit branching involved in the loop.

Test:: test_pm_sampleMean

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Amir Shahmoradi, April 21, 2017, 1:54 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 2008 of file pm_sampleMean.F90.

The documentation for this interface was generated from the following file:

src/fortran/main/pm_sampleMean.F90