This module contains classes and procedures for computing various statistical quantities related to the univariate Uniform distribution. More...

Data Types
type	distUnif_type
	This is the derived type for signifying distributions that are of type Uniform as defined in the description of pm_distUnif. More...

interface	getUnifCDF
	Generate and return the Cumulative Distribution Function (CDF) of a univariate Standard Uniform distribution or a Uniform distribution with the specified support via `lower` and `upper` input arguments at the specified input values. More...

interface	getUnifRand
	Generate and return a scalar or a `contiguous` array of rank `1` of length `s1` of randomly uniformly distributed discrete `logical`, `integer`, `character` value(s), or continuous `real` or `complex value(s) within the specified input range. More...

interface	getUnifRandState
	Generate and return an `allocatable` array of rank `1` containing the state vector of the Fortran default random number generator (RNG) or, optionally set the RNG state based on a reference input scalar seed, optionally distinctly on each processor. More...

interface	getUnifRandStateSize
	Generate and return the size of the seed vector of the Fortran default random number generator (RNG). More...

type	rngf_type
	This is a concrete derived type whose instances can be used to define/request the default uniform random number generator (RNG) of the Fortran standard. More...

interface	rngf_typer
	Generate and return a scalar object of type rngf_type. More...

type	rngu_type
	This is the `abstract` base derived type for defining various Uniform Random Number Generator (URNG) derived types. More...

interface	setUnifCDF
	Return the Cumulative Distribution Function (CDF) of a univariate Standard Uniform distribution or a Uniform distribution with the specified support via `lower` and `upper` input arguments at the specified input values. More...

interface	setUnifRand
	Return a uniform random scalar or `contiguous` array of arbitrary rank of randomly uniformly distributed discrete `logical`, `integer`, `character` value(s), or continuous `real` or `complex value(s) within the specified input range. More...

interface	setUnifRandState
	Set the state of the Fortran default random number generator (RNG) to a random value or to an optionally deterministic, optionally processor-dependent value based on the user-specified input scalar seed and processor ID. More...

type	splitmix64_type
	This is the derived type for declaring and generating objects of type splitmix64_type containing a unique instance of an splitmix64 random number generator (RNG). More...

interface	splitmix64_typer
	Generate, initialize, and return a scalar object of type splitmix64_type. More...

type	xoshiro256ss_type
	This is the `abstract` base derived type for defining variants of Xoshiro256** Uniform Random Number Generator derived types. More...

type	xoshiro256ssg_type
	This is the derived type for declaring and generating objects of type xoshiro256ssg_type containing a unique instance of a greedy Xoshiro256** random number generator (RNG). More...

interface	xoshiro256ssg_typer
	Generate, initialize, and return a scalar object of type xoshiro256ssg_type. More...

type	xoshiro256ssw_type
	This is the derived type for declaring and generating objects of type xoshiro256ssw_type containing a unique instance of a Xoshiro256** random number generator (RNG). More...

interface	xoshiro256ssw_typer
	Generate, initialize, and return a scalar object of type xoshiro256ssw_type. More...

Variables
character(*, SK), parameter	MODULE_NAME = "@pm_distUnif"

integer(IK), parameter	xoshiro256ssStreamBitSize = int(bit_size(0_IK64), IK)
	The constant scalar of type `integer` of default kind containing the number of binary digits of the `stream` component Xoshiro256** random number generator. More...

integer(IK), parameter	xoshiro256ssStateSize = 4_IK
	The constant scalar of type `integer` of default kind IK containing the size of the state vector of Xoshiro256** random number generator. More...

integer(IK64), dimension(xoshiro256ssStateSize), parameter	xoshiro256ssJump128 = [ +1733541517147835066_IK64 , -3051731464161248980_IK64 , -6244198995065845334_IK64 , +4155657270789760540_IK64 ]
	The constant vector of size xoshiro256ssStateSize of type `integer` of kind IK64 containing the state jump for the Xoshiro256** random number generator. More...

integer(IK64), dimension(xoshiro256ssStateSize), parameter	xoshiro256ssJump192 = [ +8566230491382795199_IK64 , -4251311993797857357_IK64 , +8606660816089834049_IK64 , +4111957640723818037_IK64 ]
	The constant vector of size xoshiro256ssStateSize of type `integer` of kind IK64 containing the state jump for the Xoshiro256** random number generator. More...

type(rngf_type)	rngf
	The scalar constant object of type rngf_type whose presence signified the use of the Fortran intrinsic random number generator (RNGF). More...

Detailed Description

This module contains classes and procedures for computing various statistical quantities related to the univariate Uniform distribution.

Specifically, this module contains routines for computing the following quantities of the univariate Uniform distribution:

the Probability Density Function (PDF)
the Cumulative Distribution Function (CDF)
the Random Number Generation from the distribution (RNG)
the Inverse Cumulative Distribution Function (ICDF) or the Quantile Function

The continuous uniform distributions or rectangular distributions are a family of symmetric probability distributions.
Such a distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds.
The bounds are defined by the parameters, \(a\) and \(b\), which are the minimum and maximum values.
The interval can either be closed (i.e., \([a, b]\)) or open (i.e., \((a, b)\)).
Therefore, the distribution is often abbreviated as \(U(a,b)\) where \(U\) stands for uniform distribution.
The difference between the bounds defines the interval length.
All intervals of the same length on the distribution's support are equally probable.

Note: The Uniform distribution is the maximum entropy probability distribution for a random variable \(x\) under no constraint other than that it is contained in the distribution's support.

Probability density function (PDF)

The PDF of the continuous uniform distribution is,

\begin{equation} f(x) = \begin{cases} \frac{1}{b - a} & \text{for} a\leq x \leq b ~, \\ 0 & \text{for} x < a ~ \text{or} ~ x > b ~. \end{cases} \end{equation}

The values of \(f(x)\) at the two boundaries \(a\) and \(b\) are usually unimportant, because they do not alter the value of \(\int_c^d f(x) dx\) over any interval \([c,d]\) nor of \(\int_a^b x f(x) dx\) nor of any higher moment.
Sometimes they are chosen to be zero, and sometimes chosen to be \(\frac{1}{b-a}\).
The latter is appropriate in the context of estimation by the method of maximum likelihood.
In the context of Fourier analysis, one may take the value of \(f(a)\) or \(f(b)\) to be \(\frac{1}{2(b - a)}\) because then the inverse transform of many integral transforms of this uniform function will yield back the function itself, rather than a function which is equal almost everywhere, i.e., except on a set of points with zero measure.
Also, it is consistent with the sign function, which has no such ambiguity.
Any probability density function integrates to \(1\).
Thus, the PDF of the continuous uniform distribution is graphically portrayed as a rectangle where \(b − a\) is the base length and \(\frac{1}{b-a}\) is the height.
As the base length increases, the height (the density at any particular value within the distribution boundaries) decreases.
In terms of mean \(\mu\) and variance \(\sigma^{2}\) the probability density function of the continuous uniform distribution is,

\begin{equation} f(x) = \begin{cases} \frac{1}{2\sigma\sqrt{3}} & \text{for} -\sigma\sqrt{3} \leq x - \mu \leq \sigma\sqrt{3} ~, \\ 0 & \text{otherwise} ~. \end{cases} \end{equation}

Cumulative distribution function (CDF)

The CDF of the continuous uniform distribution is,

\begin{equation} F(x) = \begin{cases} 0 & \text{for} x < a ~,\\ \frac{x - a}{b - a} & \text{for} a\leq x\leq b ~, \\ 1 & \text{for} x > b ~. \end{cases} \end{equation}

In terms of mean \(\mu\) and variance \(\sigma^{2}\), the cumulative distribution function of the continuous uniform distribution is,

\begin{equation} F(x) = \begin{cases} 0 & \text{for} x - \mu < -\sigma\sqrt{3} ~, \\ \frac{1}{2}\left(\frac{x - \mu}{\sigma\sqrt{3}} + 1\right) & \text{for} -\sigma\sqrt{3} \leq x - \mu < \sigma\sqrt{3} ~, \\ 1 & \text{for} x - \mu \geq \sigma\sqrt{3} \end{cases} \end{equation}

Note

The procedures under the generic interface getUnifCDF of this module are elemental functions that accept optional arguments of arbitrary ranks.
As such, the procedures offer great flexibility in coding.
However, the elemental nature of the procedures impacts their runtime performance negatively.
See the benchmarks below for more information.
The procedures under the generic interface setUnifCDF are subroutines that accept a limited range of specific arguments ranks.
As such, they offer much better runtime performance compared to getUnifCDF but have significantly less flexibility.
Which procedures should I use?
The elemental procedures appear to incur no performance penalty with scalar arguments. However, there appears to exist a runtime performance penalty of ~2-3 times more than the rank-specific routines for array arguments, comparable to 10-20 CPU cycles.
These penalties are due to the looping that occur in the elemental procedures for array arguments.
However, this elemental performance penalty is likely insignificant in most practical cases, unless the elemental procedures are to be called on the order of tens of billions of times in a program, in which, case, the over all performance penalty, as of 2022, appears to be on the order of a few minutes or less.
Note that the following benchmarks represent the worst case scenarios.
There may be situations where the compiler could inline the elemental procedures and remove the overhead of repeatedly calling the elemental function.

Inverse Cumulative distribution function (ICDF) or Quantile Function

The Quantile function of continuous Uniform distribution is given by,

\begin{equation} F^{-1}(p) = a + p(b - a) \quad \text{for} 0 < p < 1 ~. \end{equation}

In terms of mean \(\mu\) and variance \(\sigma^{2}\), the Quantile function of the continuous uniform distribution is,

\begin{equation} F^{-1}(p) = \sigma\sqrt{3} (2p - 1) + \mu \quad \text{for} 0 \leq p \leq 1 ~. \end{equation}

Random Number Generation (RNG)

This module contains two generic functional and subroutine interfaces

for generating uniformly distributed random values of all intrinsic types and kinds supported by the Fortran standard and the processor (character, integer, logical, complex, real).
The functional interface is merely a wrapper around the generic subroutine interface.

This module also contains four random number generator (RNG) algorithms that can be specified via the corresponding types,

rngf_type (the default intrinsic Fortran uniform RNG via random_number())
splitmix64_type
xoshiro256ssg_type
xoshiro256ssw_type

Usage

xoshiro256ssw_type is the recommended RNG for all serial and parallel tasks.
xoshiro256ssg_type is the recommended RNG for tasks that mostly require logical random values, although it can be used for random value generation of any type and kind.
splitmix64_type is the recommended RNG for initializing other RNGs or for simple serial tasks, although it can be used for random value generation of any type and kind.
The default Fortran RNG rngf_type, although flexible to use and fast, will not generate deterministic results across different compilers.

Benchmarks:

Benchmark :: The runtime performance of scalar getUnifCDF vs. setUnifCDF without bounds ⛓

program benchmark
 
    use pm_kind, only: IK, RK, SK
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i,j
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK) , parameter             :: MINITER = 10**5_IK
    integer(IK) , parameter             :: NBENCH = 2_IK
    real(RK)                            :: cdf
    real(RK)                            :: point
    real(RK)                            :: dummy = 0._RK
    type(bench_type)                    :: bench(NBENCH)
 
    bench(1) = bench_type(name = SK_"getUnifCDF", exec = getUnifCDF, overhead = setOverhead)
    bench(2) = bench_type(name = SK_"setUnifCDF", exec = setUnifCDF, overhead = setOverhead)
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "getUnifCDF() vs. setUnifCDF()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") (bench(i)%name, i = 1, NBENCH)
 
        call random_number(point)
        do i = 1, NBENCH
            bench(i)%timing = bench(i)%getTiming(miniter = MINITER)
        end do
 
        do j = 1, MINITER
            write(fileUnit,"(*(g0,:,','))") (max(epsilon(0._RK),bench(i)%timing%values(j)), i = 1, NBENCH)
        end do
 
        write(*,"(*(g0,:,' '))") dummy
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call finalize()
    end subroutine
 
    subroutine finalize()
        dummy = dummy + cdf
    end subroutine
 
    subroutine getUnifCDF()
        block
            use pm_distUnif, only: getUnifCDF
            cdf = getUnifCDF(point)
            call finalize()
        end block
    end subroutine
 
    subroutine setUnifCDF()
        block
            use pm_distUnif, only: setUnifCDF
            call setUnifCDF(cdf, point)
            call finalize()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
fontsize = 14
 
methods = ["setUnifCDF", "getUnifCDF"]
 
df = pd.read_csv("main.out")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for method in methods:
    plt.hist( np.log10(df[method].values)
            , histtype = "stepfilled"
            , density = True
            , alpha = 0.7
            , bins = 30
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("$\log_{10}$ ( Runtime [ seconds ] )", fontsize = fontsize)
ax.set_ylabel("Count", fontsize = fontsize)
ax.set_title("Rank-0 Runtime:\ngetUnifCDF vs. setUnifCDF.\nLower is better.", fontsize = fontsize)
#ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( methods
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D0.runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.hist( np.log10(df["getUnifCDF"].values / df["setUnifCDF"].values)
        , histtype = "stepfilled"
        , density = True
        , alpha = 0.7
        , bins = 30
        )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(r"$\log_{10}$ ( Runtime Ratio [ seconds ] )", fontsize = fontsize)
ax.set_ylabel("Count", fontsize = fontsize)
ax.set_title(r"""$\log_{10}$ ( Rank-0 Runtime Ratio ): getUnifCDF to setUnifCDF.
A value < $\log_{10}(1)$ implies better performance of getUnifCDF.""", fontsize = fontsize)
#ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D0.runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The procedures under the generic interface getUnifCDF are elemental functions with optional arguments. In the absence of the optional arguments, the default values are used, but the associated computations will be redundant.
As such, one expects the getUnifCDF to perform less efficiently than the procedures under the generic interface setUnifCDF which are rank-specific and carefully designed to avoid redundant computations.

Benchmark :: The runtime performance of array getUnifCDF vs. setUnifCDF without bounds ⛓

program benchmark
 
    use pm_kind, only: IK, RK, SK
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK) , parameter             :: NARR = 16_IK
    integer(IK) , parameter             :: NBENCH = 2_IK
    integer(IK)                         :: arraySize(NARR)
    real(RK)    , allocatable           :: cdf(:)
    real(RK)    , allocatable           :: point(:)
    real(RK)                            :: dummy = 0._RK
    type(bench_type)                    :: bench(NBENCH)
 
    bench(1) = bench_type(name = SK_"getUnifCDF", exec = getUnifCDF, overhead = setOverhead)
    bench(2) = bench_type(name = SK_"setUnifCDF", exec = setUnifCDF, overhead = setOverhead)
 
    arraySize = [( 2_IK**iarr, iarr = 1_IK, NARR )]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "getUnifCDF() vs. setUnifCDF()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "arraySize", (bench(i)%name, i = 1, NBENCH)
 
        loopOverMatrixSize: do iarr = 1, NARR
 
            write(*,"(*(g0,:,' '))") "Benchmarking getUnifCDF() vs. setUnifCDF() with array size", arraySize(iarr)
            allocate(cdf(arraySize(iarr)), point(arraySize(iarr)))
            call random_number(point)
 
            do i = 1, NBENCH
                bench(i)%timing = bench(i)%getTiming()
            end do
 
            deallocate(cdf, point)
            write(fileUnit,"(*(g0,:,','))") arraySize(iarr), (bench(i)%timing%mean, i = 1, NBENCH)
 
        end do loopOverMatrixSize
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call finalize()
    end subroutine
 
    subroutine finalize()
        dummy = dummy + sum(cdf)
    end subroutine
 
    subroutine getUnifCDF()
        block
            use pm_distUnif, only: getUnifCDF
            cdf(:) = getUnifCDF(point)
            call finalize()
        end block
    end subroutine
 
    subroutine setUnifCDF()
        block
            use pm_distUnif, only: setUnifCDF
            call setUnifCDF(cdf, point)
            call finalize()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
fontsize = 14
 
methods = ["setUnifCDF", "getUnifCDF"]
 
df = pd.read_csv("main.out")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for method in methods:
    plt.plot( df["arraySize"].values
            , df[method].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("Array Size", fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title("Rank-1 Runtime:\ngetUnifCDF vs. setUnifCDF.\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( methods
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D1.runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df["arraySize"].values
        , np.ones( len(df["arraySize"].values) )
        , linestyle = "-"
        , linewidth = 2
       #, color = "black"
        )
plt.plot( df["arraySize"].values
        , df["getUnifCDF"].values / df["setUnifCDF"].values
        , linewidth = 2
       #, color = "r"
        )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("Array Size", fontsize = fontsize)
ax.set_ylabel("Runtime Ratio", fontsize = fontsize)
ax.set_title("""Rank-1 Runtime Ratio: getUnifCDF to setUnifCDF.
A value < 1 implies better performance of getUnifCDF.""", fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( ["setUnifCDF", "getUnifCDF"]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D1.runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The procedures under the generic interface getUnifCDF are elemental functions with optional arguments.
In the absence of the optional arguments, the default values are used, but the associated computations will be redundant.
Furthermore, elemental functions incur a performance penalty for input array arguments due to internal looping performed by the compiler to call the function repeatedly for different array elements.
As such, one expects the getUnifCDF to perform less efficiently than the procedures under the generic interface setUnifCDF which are rank-specific and carefully designed to avoid redundant computations.

Benchmark :: The runtime performance of scalar getUnifCDF vs. setUnifCDF with bounds ⛓

program benchmark
 
    use pm_kind, only: IK, RK, SK
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i,j
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK) , parameter             :: MINITER = 10**5_IK
    integer(IK) , parameter             :: NBENCH = 2_IK
    real(RK)    , parameter             :: LOWER = -2._RK
    real(RK)    , parameter             :: UPPER = +2._RK
    real(RK)                            :: cdf
    real(RK)                            :: point
    real(RK)                            :: dummy = 0._RK
    type(bench_type)                    :: bench(NBENCH)
 
    bench(1) = bench_type(name = SK_"getUnifCDF", exec = getUnifCDF, overhead = setOverhead)
    bench(2) = bench_type(name = SK_"setUnifCDF", exec = setUnifCDF, overhead = setOverhead)
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "getUnifCDF() vs. setUnifCDF()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") (bench(i)%name, i = 1, NBENCH)
 
        call random_number(point)
        do i = 1, NBENCH
            bench(i)%timing = bench(i)%getTiming(miniter = MINITER)
        end do
 
        do j = 1, MINITER
            write(fileUnit,"(*(g0,:,','))") (max(epsilon(0._RK),bench(i)%timing%values(j)), i = 1, NBENCH)
        end do
 
        write(*,"(*(g0,:,' '))") dummy
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call finalize()
    end subroutine
 
    subroutine finalize()
        dummy = dummy + cdf
    end subroutine
 
    subroutine getUnifCDF()
        block
            use pm_distUnif, only: getUnifCDF
            cdf = getUnifCDF(point, LOWER, UPPER)
            call finalize()
        end block
    end subroutine
 
    subroutine setUnifCDF()
        block
            use pm_distUnif, only: setUnifCDF
            call setUnifCDF(cdf, point, LOWER, UPPER)
            call finalize()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
fontsize = 14
 
methods = ["setUnifCDF", "getUnifCDF"]
 
df = pd.read_csv("main.out")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for method in methods:
    plt.hist( np.log10(df[method].values)
            , histtype = "stepfilled"
            , density = True
            , alpha = 0.7
            , bins = 30
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("$\log_{10}$ ( Runtime [ seconds ] )", fontsize = fontsize)
ax.set_ylabel("Count", fontsize = fontsize)
ax.set_title("Rank-0 Runtime:\ngetUnifCDF vs. setUnifCDF.\nLower is better.", fontsize = fontsize)
#ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( methods
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D0_D0.runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.hist( np.log10(df["getUnifCDF"].values / df["setUnifCDF"].values)
        , histtype = "stepfilled"
        , density = True
        , alpha = 0.7
        , bins = 30
        )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(r"$\log_{10}$ ( Runtime Ratio [ seconds ] )", fontsize = fontsize)
ax.set_ylabel("Count", fontsize = fontsize)
ax.set_title(r"""$\log_{10}$ ( Rank-0 Runtime Ratio ): getUnifCDF to setUnifCDF.
A value < $\log_{10}(1)$ implies better performance of getUnifCDF.""", fontsize = fontsize)
#ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D0_D0.runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The procedures under the generic interface getUnifCDF are elemental functions with optional arguments.
In the presence of the optional arguments, the user-specified values are used.
Therefore, the costs of computations in getUnifCDF are more comparable to the procedures under the generic interface setUnifCDF which are rank-specific and carefully designed to avoid redundant computations.

Benchmark :: The runtime performance of array getUnifCDF vs. setUnifCDF with bounds ⛓

program benchmark
 
    use pm_kind, only: IK, RK, SK
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK) , parameter             :: NARR = 16_IK
    integer(IK) , parameter             :: NBENCH = 2_IK
    integer(IK)                         :: arraySize(NARR)
    real(RK)    , parameter             :: LOWER = -2._RK
    real(RK)    , parameter             :: UPPER = +2._RK
    real(RK)    , allocatable           :: cdf(:)
    real(RK)    , allocatable           :: Point(:)
    real(RK)                            :: dummy = 0._RK
    type(bench_type)                    :: bench(NBENCH)
 
    bench(1) = bench_type(name = SK_"getUnifCDF", exec = getUnifCDF, overhead = setOverhead)
    bench(2) = bench_type(name = SK_"setUnifCDF", exec = setUnifCDF, overhead = setOverhead)
 
    arraySize = [( 2_IK**iarr, iarr = 1_IK, NARR )]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "getUnifCDF() vs. setUnifCDF()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "arraySize", (bench(i)%name, i = 1, NBENCH)
 
        loopOverMatrixSize: do iarr = 1, NARR
 
            write(*,"(*(g0,:,' '))") "Benchmarking getUnifCDF() vs. setUnifCDF() with array size", arraySize(iarr)
            allocate(cdf(arraySize(iarr)), Point(arraySize(iarr)))
            call random_number(Point)
 
            do i = 1, NBENCH
                bench(i)%timing = bench(i)%getTiming()
            end do
 
            deallocate(cdf, Point)
            write(fileUnit,"(*(g0,:,','))") arraySize(iarr), (bench(i)%timing%mean, i = 1, NBENCH)
 
        end do loopOverMatrixSize
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call finalize()
    end subroutine
 
    subroutine finalize()
        dummy = dummy + sum(cdf)
    end subroutine
 
    subroutine getUnifCDF()
        block
            use pm_distUnif, only: getUnifCDF
            cdf(:) = getUnifCDF(Point, LOWER, UPPER)
            call finalize()
        end block
    end subroutine
 
    subroutine setUnifCDF()
        block
            use pm_distUnif, only: setUnifCDF
            call setUnifCDF(cdf, Point, LOWER, UPPER)
            call finalize()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
fontsize = 14
 
methods = ["setUnifCDF", "getUnifCDF"]
 
df = pd.read_csv("main.out")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for method in methods:
    plt.plot( df["arraySize"].values
            , df[method].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("Array Size", fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title("Rank-1 Runtime:\ngetUnifCDF vs. setUnifCDF.\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( methods
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D1_D0.runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df["arraySize"].values
        , np.ones( len(df["arraySize"].values) )
        , linestyle = "-"
        , linewidth = 2
       #, color = "black"
        )
plt.plot( df["arraySize"].values
        , df["getUnifCDF"].values / df["setUnifCDF"].values
        , linewidth = 2
       #, color = "r"
        )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("Array Size", fontsize = fontsize)
ax.set_ylabel("Runtime Ratio", fontsize = fontsize)
ax.set_title("""Rank-1 Runtime Ratio: getUnifCDF to setUnifCDF.
A value < 1 implies better performance of getUnifCDF.""", fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( ["setUnifCDF", "getUnifCDF"]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.getUnifCDF_vs_setUnifCDF_D1_D0.runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The procedures under the generic interface getUnifCDF are elemental functions with optional arguments.
In the presence of the optional arguments, the user-specified values are used.
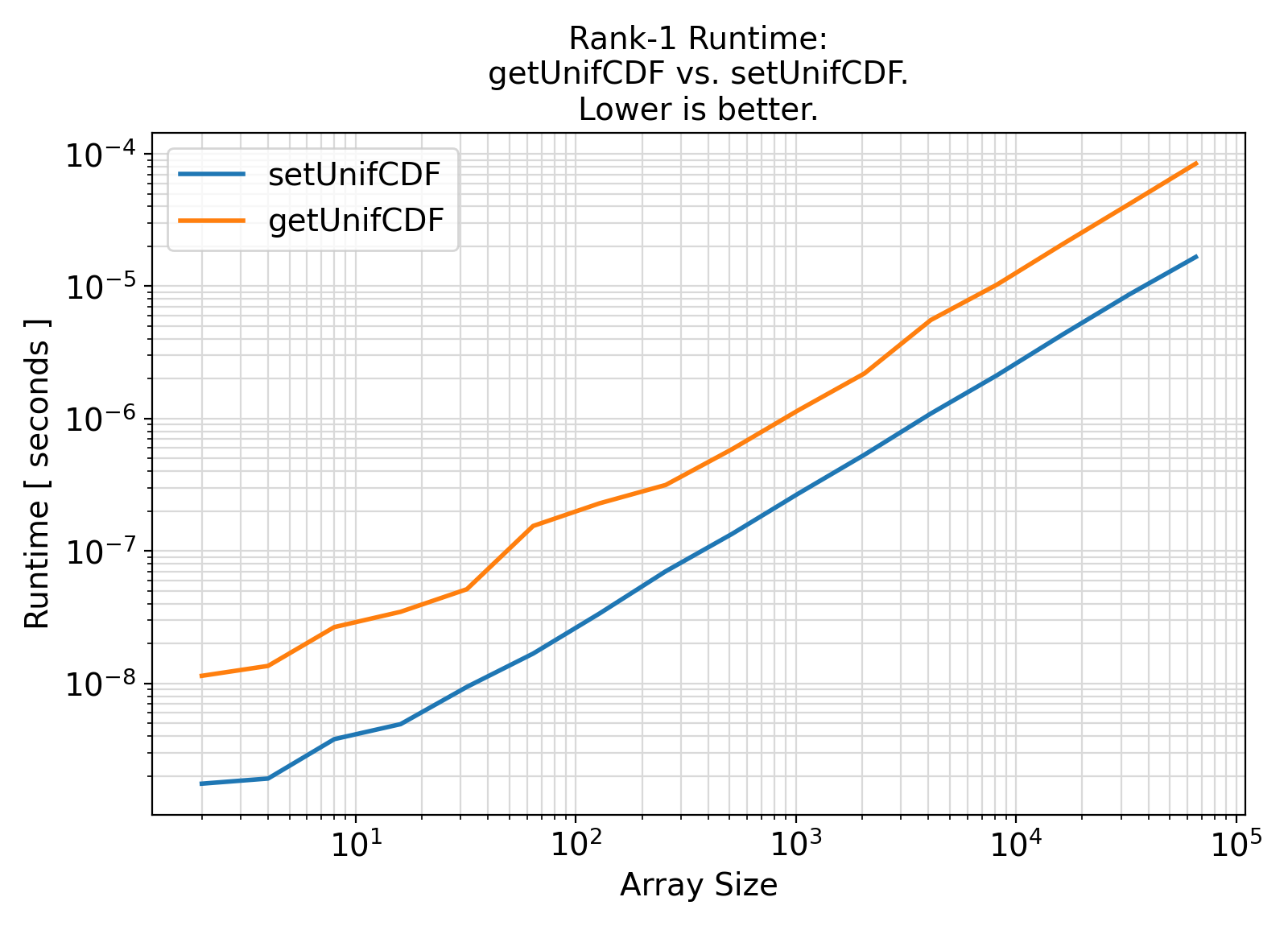
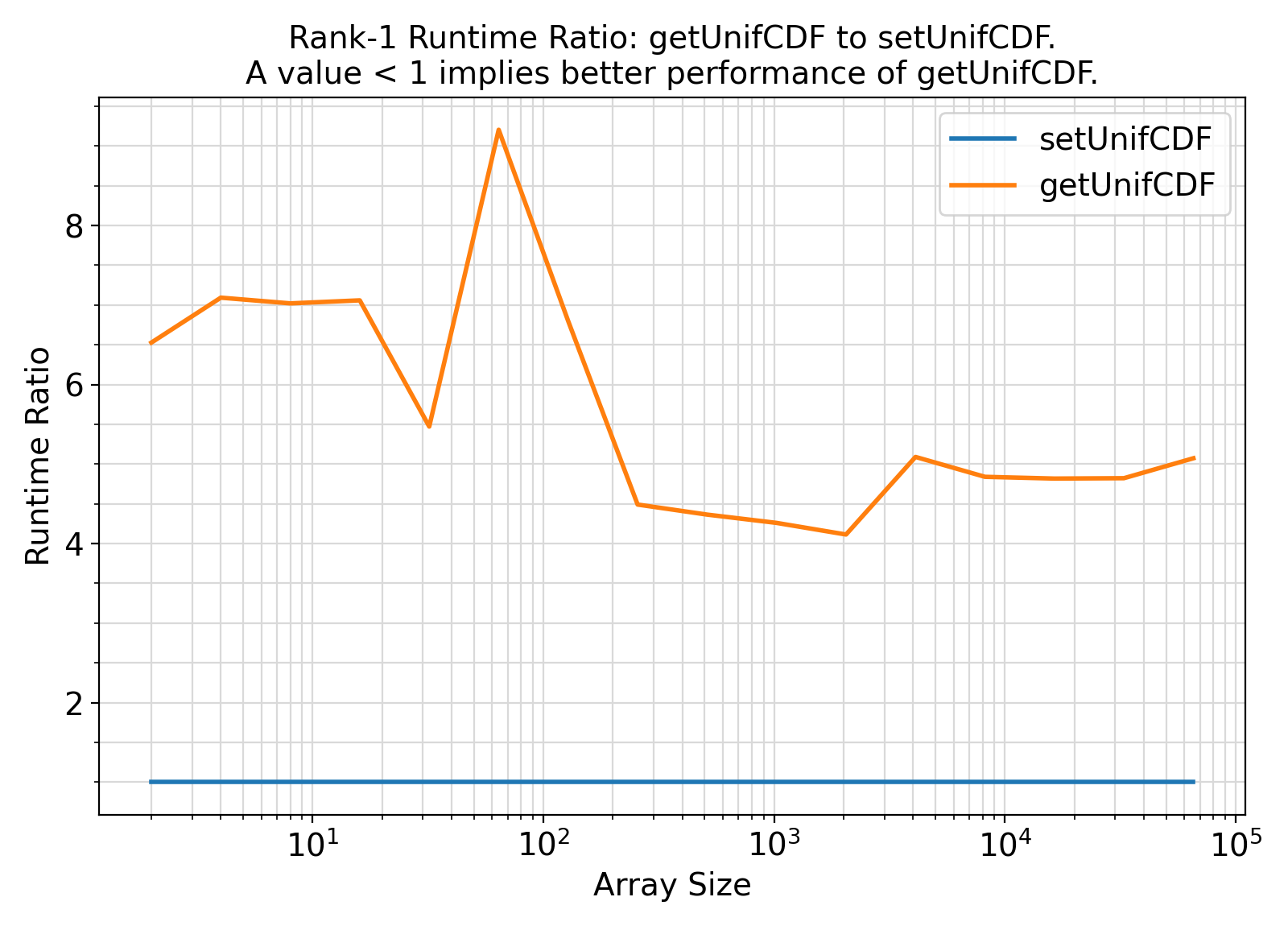
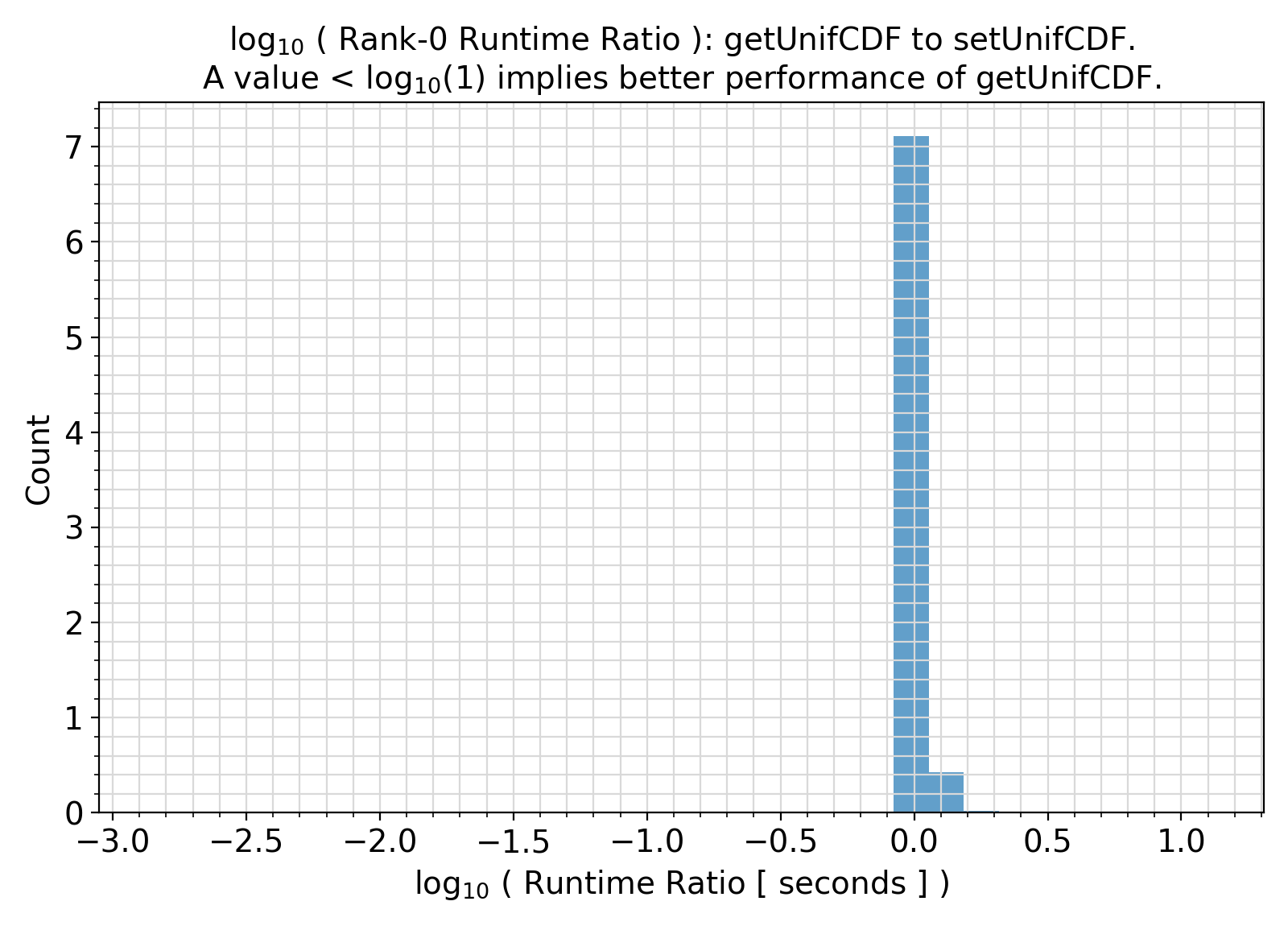
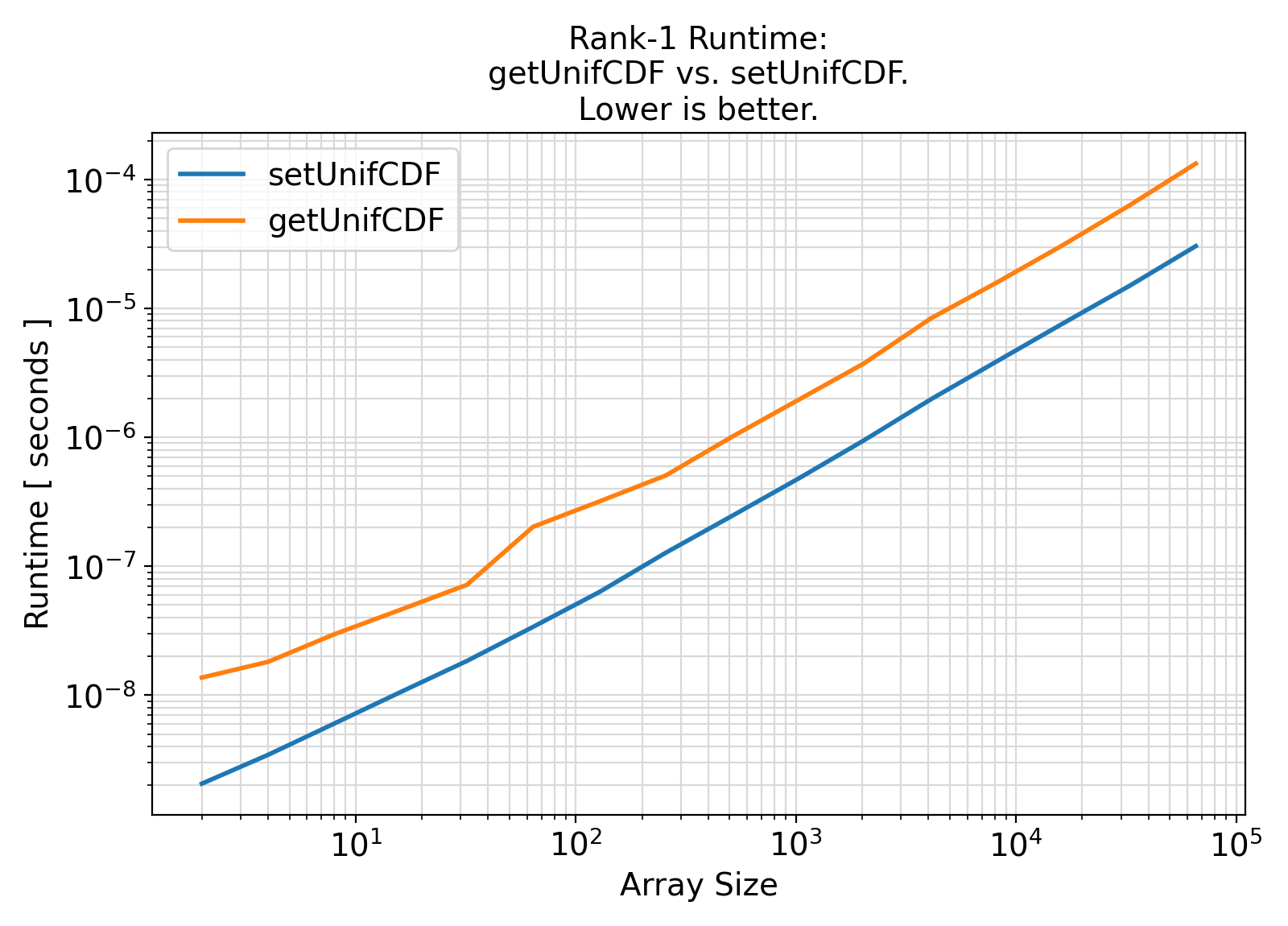
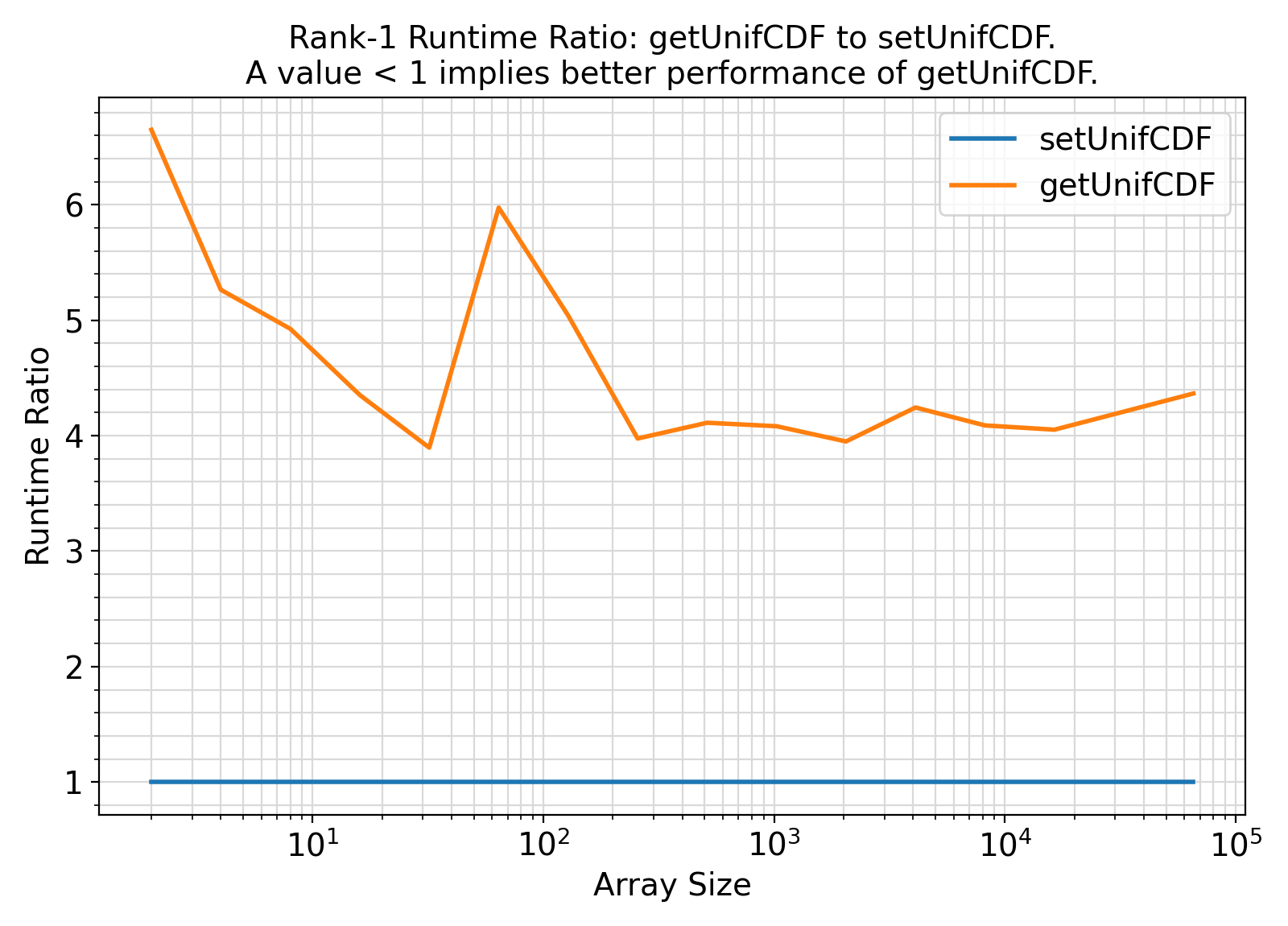
Although the elemental functions incur a performance penalty for input array arguments due to internal looping performed by the compiler to call the function repeatedly for different array elements, the costs of computations in getUnifCDF become more comparable to the procedures under the generic interface setUnifCDF which are rank-specific and carefully designed to avoid redundant computations.

Benchmark :: The runtime performance of setUnifRand vs. Fortran intrinsic random_number(). ⛓

! Test the overhead of calling `setUnifRand()` vs. Fortran intrinsic procedure `random_number()`.
program benchmark
 
    use pm_kind, only: IK, RK, SK
    use pm_bench, only: bench_type
    use pm_distUnif, only: setUnifRand, xoshiro256ssw_type
 
    implicit none
 
    type(xoshiro256ssw_type)            :: rngx
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK)     , parameter         :: NARR = 11_IK
    integer(IK)                         :: arraySize(NARR)
    real(RK)        , allocatable       :: rand(:)
    real(RK)                            :: dummy = 0._RK
    type(bench_type), allocatable       :: bench(:)
 
    rngx = xoshiro256ssw_type()
    bench = [ bench_type(name = SK_"random_number ", exec = random_number, overhead = setOverhead) &
            , bench_type(name = SK_"setUnifRandRNGD", exec = setUnifRandRNGD, overhead = setOverhead) &
            , bench_type(name = SK_"setUnifRandRNGX", exec = setUnifRandRNGX, overhead = setOverhead) &
            ]
 
    arraySize = [( 2_IK**iarr, iarr = 1_IK, NARR )]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "setUnifRand() vs. random_number()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "arraySize", (bench(i)%name, i = 1, size(bench))
 
        loopOverMatrixSize: do iarr = 1, NARR
 
            allocate(rand(arraySize(iarr)))
            write(*,"(*(g0,:,' '))") "Benchmarking setUnifRand() vs. random_number() with array size", arraySize(iarr)
 
            do i = 1, size(bench)
                bench(i)%timing = bench(i)%getTiming()
            end do
 
            write(fileUnit,"(*(g0,:,','))") arraySize(iarr), (bench(i)%timing%mean, i = 1, size(bench))
            deallocate(rand)
 
        end do loopOverMatrixSize
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call getDummy()
    end subroutine
 
    subroutine getDummy()
        dummy = dummy + rand(1)
    end subroutine
 
    subroutine setUnifRandRNGD()
        block
            call setUnifRand(rand)
            call getDummy()
        end block
    end subroutine
 
    subroutine setUnifRandRNGX()
        block
            call setUnifRand(rngx, rand)
            call getDummy()
        end block
    end subroutine
 
    subroutine random_number()
        block
            intrinsic :: random_number
            call random_number(rand)
            call getDummy()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
fontsize = 14
 
df = pd.read_csv("main.out")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df.values[:, 0]
        , df.values[:,1:]
        , linewidth = 2
        )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("Array Size", fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title("Runtime:\nsetUnifRand() vs. random_number().\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( list(df.columns.values[1:])
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.setUnifRand_vs_random_number.runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
# baseline
 
plt.plot( df.values[:, 0]
        , np.ones( len(df["arraySize"].values) )
        , linestyle = "-"
        , linewidth = 2
        )
for colname in df.columns.values[2:]:
    plt.plot( df.values[:, 0]
            , df[colname].values / df.values[:, 1]
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("Array Size", fontsize = fontsize)
ax.set_ylabel("Runtime Ratio", fontsize = fontsize)
ax.set_title("""Uniform RNG Runtime Ratio: setUnifRand() to random_number().
A value < 1 implies better performance of setUnifRand().""", fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( list(df.columns.values[1:])
           #, bbox_to_anchor=(1, 0.5)
           #, loc='center left'
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark.setUnifRand_vs_random_number.runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The default RNG in the procedures under the generic interface setUnifRand are simply wrappers around the intrinsic random number generator of Fortran random_number().
As such, setUnifRand for generating random real numbers has \(\ms{5-10%}\) overhead with respect to the intrinsic random_number().
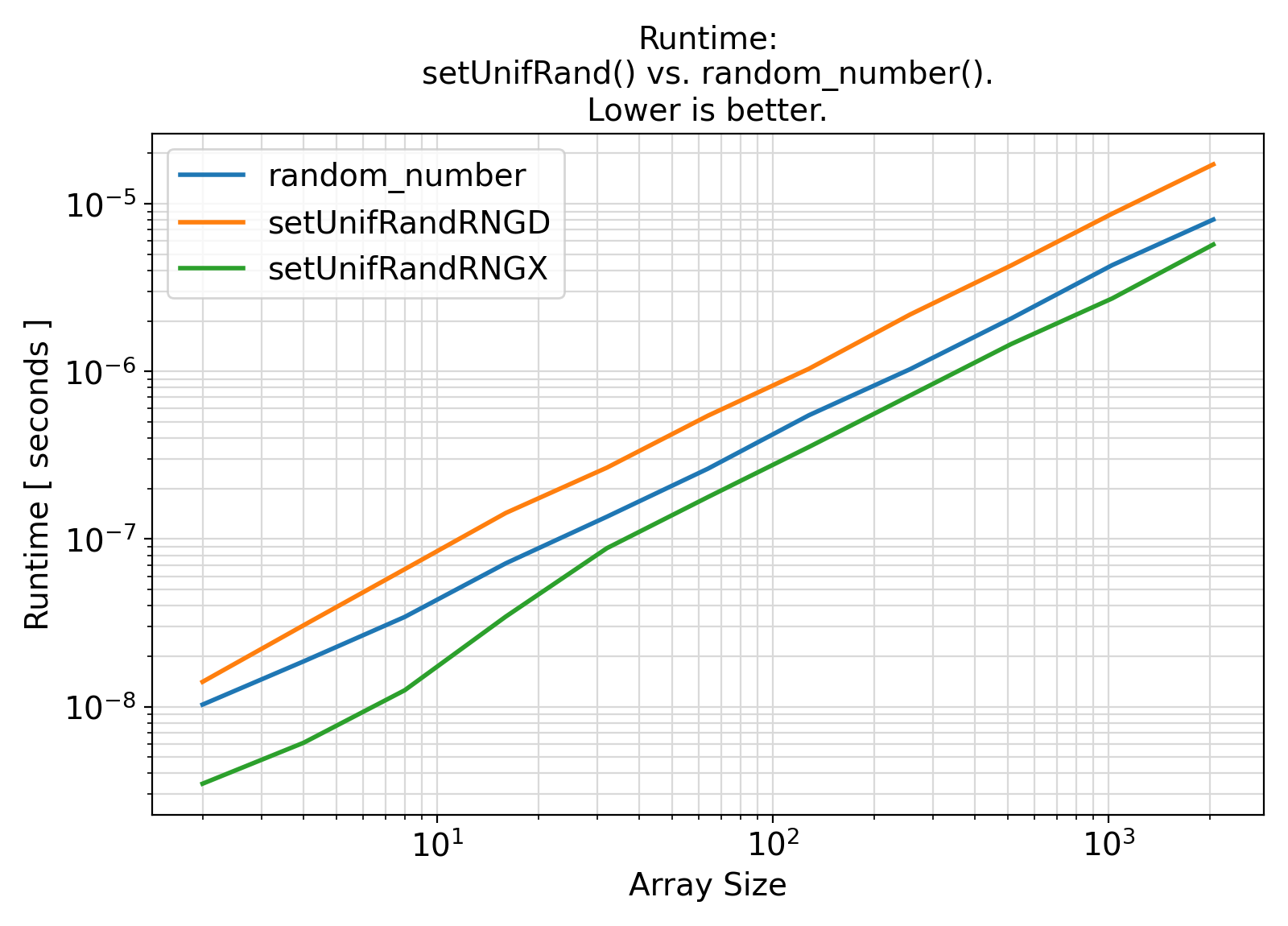
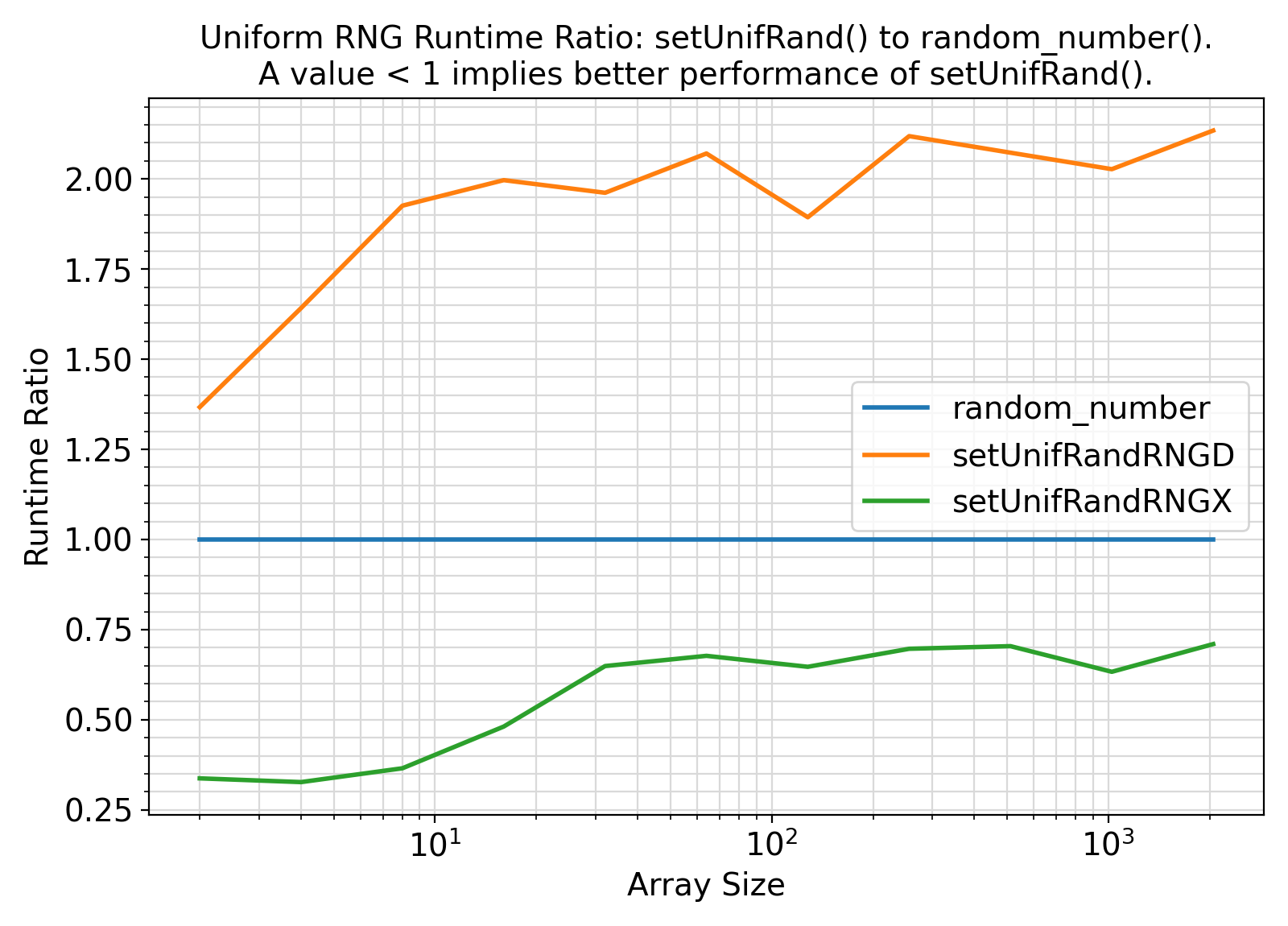
Note Fortran does not have integer, logical, complex, or character uniform random RNG whereas setUnifRand provides a unified API for random numbers of all types.
The RNGX is an acronym for xoshiro256ssw_type in the procedures under the generic interface setUnifRand.
This random number generator, although unsafe for cryptographic purposes, is quite competitive and performant, even compared to the intrinsic Fortran compiler RNGs.

Benchmark :: The runtime performance of intrinsic random_number() vs. splitmix64_type vs. xoshiro256ssw_type. ⛓

program benchmark
 
    use pm_kind, only: SK, IK, LK, RKG => RK, IKG => IK, LKG => LK
    use pm_distUnif, only: splitmix64_type
    use pm_distUnif, only: xoshiro256ssw_type
    use pm_distUnif, only: setUnifRand
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i, j, fileUnit
    integer(IK)         , parameter     :: NSIM = 100000_IK
    logical(LKG)                        :: dumm_LK = .false._LKG
    logical(LKG)                        :: rand_LK(NSIM)
    integer(IKG)                        :: rand_IK(NSIM)
    real(RKG)                           :: rand_RK(NSIM)
    type(bench_type)    , allocatable   :: bench(:)
    type(splitmix64_type)            :: splitmix64
    type(xoshiro256ssw_type)            :: xoshiro256ssw
    splitmix64 = splitmix64_type()
    xoshiro256ssw = xoshiro256ssw_type()
 
    bench = [ bench_type(name = SK_"random_number_LK", exec = random_number_LK, overhead = setOverhead_LK) &
            , bench_type(name = SK_"splitmix64_type_LK", exec = splitmix64_type_LK, overhead = setOverhead_LK) &
            , bench_type(name = SK_"xoshiro256ssw_type_LK", exec = xoshiro256ssw_type_LK, overhead = setOverhead_LK) &
            , bench_type(name = SK_"random_number_IK", exec = random_number_IK, overhead = setOverhead_LK) &
            , bench_type(name = SK_"splitmix64_type_IK", exec = splitmix64_type_IK, overhead = setOverhead_IK) &
            , bench_type(name = SK_"xoshiro256ssw_type_IK", exec = xoshiro256ssw_type_IK, overhead = setOverhead_IK) &
            , bench_type(name = SK_"random_number_RK", exec = random_number_RK, overhead = setOverhead_RK) &
            , bench_type(name = SK_"splitmix64_type_RK", exec = splitmix64_type_RK, overhead = setOverhead_RK) &
            , bench_type(name = SK_"xoshiro256ssw_type_RK", exec = xoshiro256ssw_type_RK, overhead = setOverhead_RK) &
            ]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "splitmix64_type() vs. xoshiro256ssw_type()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") (bench(i)%name, i = 1, size(bench))
        do i = 1, size(bench)
            bench(i)%timing = bench(i)%getTiming()
        end do
        do j = 1, minval([(size(bench(i)%timing%values), i = 1, size(bench))])
            write(fileUnit,"(*(g0,:,','))") (bench(i)%timing%values(j) / NSIM, i = 1, size(bench))
        end do
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead_LK()
        call getDummy_LK()
    end subroutine
 
    subroutine setOverhead_IK()
        call getDummy_IK()
    end subroutine
 
    subroutine setOverhead_RK()
        call getDummy_RK()
    end subroutine
 
    subroutine getDummy_LK()
        dumm_LK = dumm_LK .or. count(rand_LK) == 0
    end subroutine
 
    subroutine getDummy_IK()
        dumm_LK = dumm_LK .or. any(rand_IK == 0_IKG)
    end subroutine
 
    subroutine getDummy_RK()
        dumm_LK = dumm_LK .or. any(rand_RK == 0._RKG)
    end subroutine
 
    subroutine random_number_LK()
#if     1
        call setUnifRand(rand_LK)
#else
        block
            real :: rand
            call random_number(rand)
            rand_LK = logical(rand < 0.5, LKG)
            call getDummy_LK()
        end block
#endif
    end subroutine
 
    subroutine splitmix64_type_LK()
        call setUnifRand(splitmix64, rand_LK)
        call getDummy_LK()
    end subroutine
 
    subroutine xoshiro256ssw_type_LK()
        call setUnifRand(xoshiro256ssw, rand_LK)
        call getDummy_LK()
    end subroutine
 
 
    subroutine random_number_IK()
        call setUnifRand(rand_IK)
        call getDummy_IK()
    end subroutine
 
    subroutine splitmix64_type_IK()
        call setUnifRand(splitmix64, rand_IK)
        call getDummy_IK()
    end subroutine
 
    subroutine xoshiro256ssw_type_IK()
        call setUnifRand(xoshiro256ssw, rand_IK)
        call getDummy_IK()
    end subroutine
 
 
    subroutine random_number_RK()
        call setUnifRand(rand_RK)
        call getDummy_RK()
    end subroutine
 
    subroutine splitmix64_type_RK()
        call setUnifRand(splitmix64, rand_RK)
        call getDummy_RK()
    end subroutine
 
    subroutine xoshiro256ssw_type_RK()
        call setUnifRand(xoshiro256ssw, rand_RK)
        call getDummy_RK()
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ",")
colnames = list(df.columns.values)
 
df = pd.read_csv("main.out")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames:
    plt.hist( np.log10(df[colname].values)
            , histtype = "stepfilled"
           #, density = True
            , alpha = 0.7
           #, bins = 30
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel("$\log_{10}$ ( Runtime [ seconds ] )", fontsize = fontsize)
ax.set_ylabel("Count", fontsize = fontsize)
#ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
#ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.hist( np.log10(df[colname].values / df[colnames[0]].values)
            , histtype = "stepfilled"
           #, density = True
            , alpha = 0.7
           #, bins = 30
            )
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[0]), fontsize = fontsize)
ax.set_xlabel(r"$\log_{{10}}$ ( Runtime Ratio ) w.r.t. {}".format(colnames[0]), fontsize = fontsize)
ax.set_ylabel("Count", fontsize = fontsize)
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The xoshiro256ssg_type RNG greedily attempts to use as many randomly generated bits as possible in the output random values.
The xoshiro256ssw_type RNG takes a wasteful approach of using at least one or more chunks of 64 randomly generated bits in the output random values.
This fundamental difference between the two RNG types generally leads to faster random logical value generations with the greedy approach, because 64bits chunks translate to 64 logical values without updating the RNG state.
However, the greedy approach leads to generally slower runtimes for real random value generation.
Both greedy and wasteful RNGs appear to be much faster than the ParaMonte library wrappers for the implementations offered by GNU Fortran Compiler gfortran and Intel Classic Fortran Compiler ifort.
Moral: If your application requires many logical random number generation, use the greedy xoshiro256ssg_type RNG.
Conversely, if your application requires a mixture of random number generations of various types and kinds, use the wasteful xoshiro256ssw_type RNG.

Test:: test_pm_distUnif

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan

Variable Documentation

◆ MODULE_NAME

character(*, SK), parameter pm_distUnif::MODULE_NAME = "@pm_distUnif"

Definition at line 284 of file pm_distUnif.F90.

◆ rngf

type(rngf_type) pm_distUnif::rngf

The scalar constant object of type rngf_type whose presence signified the use of the Fortran intrinsic random number generator (RNGF).

This constant is merely a convenience for making easier calls to routines that require a default RNGF.

Possible calling interfaces ⛓

: use pm_distUnif, only: rngf, rngf_type

type(rngf_type) :: rng = rngf

pm_distUnif::rngf
type(rngf_type) rngf
The scalar constant object of type rngf_type whose presence signified the use of the Fortran intrinsi...
Definition: pm_distUnif.F90:2886

pm_distUnif::rngf_type
This is a concrete derived type whose instances can be used to define/request the default uniform ran...
Definition: pm_distUnif.F90:2837

See also: rngf
isHead
getUnifCDF
getUnifRand
setUnifRand
getUnifRandState
setUnifRandState
rngu_type
rngf_type
splitmix64_type
xoshiro256ssw_type
getUnifRandStateSize

Bug:: Status: Unresolved
Source: Intel Classic Fortran Compiler ifort version 2021.8.0 20221119
Description: Intel Classic Fortran Compiler ifort cannot handle the creation of a module constant of type rngf_type as done for this object, yielding the following error.

error #9066: A generic function reference is not permitted in a constant expression. [CONSTRUCTFRNG]

GNU compiler compiles and runs the code without complaining.

Remedy (as of ParaMonte Library version 2.0.0): For now, the parameter attribute is removed from the declaration of rngf.

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Amir Shahmoradi, September 1, 2017, 12:00 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 2886 of file pm_distUnif.F90.

◆ xoshiro256ssJump128

integer(IK64), dimension(xoshiro256ssStateSize), parameter pm_distUnif::xoshiro256ssJump128 = [ +1733541517147835066_IK64 , -3051731464161248980_IK64 , -6244198995065845334_IK64 , +4155657270789760540_IK64 ]

The constant vector of size xoshiro256ssStateSize of type integer of kind IK64 containing the state jump for the Xoshiro256** random number generator.

This state jump can be passed to the constructor of xoshiro256ssw_type to request an RNG whose state starts at imageID * 2**128 steps (i.e., random number generations) ahead of the RNG constructed with imageID = 1.
Using this jump, one can generate 2**128 independent RNG sequences each of which has a period of 2**128 in parallel applications.
For more information see the documentation of xoshiro256ssg_type and xoshiro256ssw_type.

The elements of this constant vector are obtained by transferring the following unsigned integers to signed values.

integer(IK64)   , parameter :: xoshiro256ssJump128(xoshiro256ssStateSize) = [ transfer(Z"180ec6d33cfd0aba", 0_IK64) &
                                                                            , transfer(Z"d5a61266f0c9392c", 0_IK64) &
                                                                            , transfer(Z"a9582618e03fc9aa", 0_IK64) &
                                                                            , transfer(Z"39abdc4529b1661c", 0_IK64) ]

See also: xoshiro256ssw_type
xoshiro256ssJump128
xoshiro256ssJump192
xoshiro256ssw_typer
xoshiro256ssStateSize

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Fatemeh Bagheri, Wednesday 12:20 AM, October 13, 2021, Dallas, TX

Definition at line 2675 of file pm_distUnif.F90.

◆ xoshiro256ssJump192

integer(IK64), dimension(xoshiro256ssStateSize), parameter pm_distUnif::xoshiro256ssJump192 = [ +8566230491382795199_IK64 , -4251311993797857357_IK64 , +8606660816089834049_IK64 , +4111957640723818037_IK64 ]

The constant vector of size xoshiro256ssStateSize of type integer of kind IK64 containing the state jump for the Xoshiro256** random number generator.

This state jump can be passed to the constructor of xoshiro256ssw_type to request an RNG whose state starts at imageID * 2**192 steps (i.e., random number generations) ahead of the RNG constructed with imageID = 1.
Using this jump, one can generate 2**64 independent RNG sequences each of which has a period of 2**192 in parallel applications.
For more information see the documentation of xoshiro256ssg_type and xoshiro256ssw_type.

The elements of this constant vector are obtained by transferring the following unsigned integers to signed values.

integer(IK64)   , parameter :: xoshiro256ssJump192(xoshiro256ssStateSize) = [ transfer(Z"76e15d3efefdcbbf", 0_IK64) &
                                                                            , transfer(Z"c5004e441c522fb3", 0_IK64) &
                                                                            , transfer(Z"77710069854ee241", 0_IK64) &
                                                                            , transfer(Z"39109bb02acbe635", 0_IK64) ]

See also: xoshiro256ssw_type
xoshiro256ssJump128
xoshiro256ssJump192
xoshiro256ssw_typer
xoshiro256ssStateSize

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Fatemeh Bagheri, Wednesday 12:20 AM, October 13, 2021, Dallas, TX

Definition at line 2715 of file pm_distUnif.F90.

◆ xoshiro256ssStateSize

integer(IK), parameter pm_distUnif::xoshiro256ssStateSize = 4_IK

The constant scalar of type integer of default kind IK containing the size of the state vector of Xoshiro256** random number generator.

For more information see the documentation of xoshiro256ssg_type and xoshiro256ssw_type.

See also: xoshiro256ssw_type
xoshiro256ssJump128
xoshiro256ssJump192
xoshiro256ssw_typer
xoshiro256ssStateSize

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Fatemeh Bagheri, Wednesday 12:20 AM, October 13, 2021, Dallas, TX

Definition at line 2641 of file pm_distUnif.F90.

◆ xoshiro256ssStreamBitSize

integer(IK), parameter pm_distUnif::xoshiro256ssStreamBitSize = int(bit_size(0_IK64), IK)

The constant scalar of type integer of default kind containing the number of binary digits of the stream component Xoshiro256** random number generator.

By definition, this number is 64, because the type kind parameter of stream is IK64.

See also: xoshiro256ssw_type
xoshiro256ssJump128
xoshiro256ssJump192
xoshiro256ssw_typer
xoshiro256ssStateSize

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Fatemeh Bagheri, Wednesday 12:20 AM, October 13, 2021, Dallas, TX

Definition at line 2619 of file pm_distUnif.F90.

Data Types

Variables

Detailed Description

Variable Documentation

◆ MODULE_NAME

◆ rngf

◆ xoshiro256ssJump128

◆ xoshiro256ssJump192

◆ xoshiro256ssStateSize

◆ xoshiro256ssStreamBitSize