
|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |

|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
This module contains classes and procedures for computing various statistical quantities related to the univariate Normal distribution. More...
Data Types | |
| type | distNorm_type |
| This is the derived type for signifying distributions that are of type Univariate Normal as defined in the description of pm_distNorm. More... | |
| interface | getNormCDF |
| Generate and return the Cumulative Distribution Function (CDF) of the univariate Normal distribution. More... | |
| interface | getNormEntropy |
| Generate and return the entropy of the Normal distribution with the input natural logarithm of the variance. More... | |
| interface | getNormFisher |
| Generate the Fisher Information of the Normal distribution. More... | |
| interface | getNormKLD |
| Generate and return the Kullback-Leibler Divergence (KLD) D_{KL}(P \parallel Q) of a given univariate Normal distribution Q from a reference Normal distribution P. More... | |
| interface | getNormLogPDF |
| Generate the natural logarithm of probability density function (PDF) of the univariate Normal distribution. More... | |
| interface | getNormQuan |
| Generate and return the Normal Quantile corresponding to the input CDF of the univariate Normal distribution. More... | |
| interface | getNormRand |
Generate and return a scalar or array of arbitrary rank of random values from the univariate Normal distribution with the specified input mean and optionally, with the specified input standard deviation std of the Normal distribution. More... | |
| interface | getZigNorm |
| Generate and return the lower right edges of the rectangles of a Ziggurat partitioning of the Normal density function (and the corresponding density function values) to be used for Normal random number generation using the Ziggurat algorithm. More... | |
| interface | setNormCDF |
| Generate and return the Cumulative Distribution Function (CDF) of the univariate Normal distribution. More... | |
| interface | setNormLogPDF |
| Generate the natural logarithm of probability density function (PDF) of the univariate Normal distribution. More... | |
| interface | setNormQuan |
| Generate and return the quantile of the univariate Normal distribution at the specified input CDF. More... | |
| interface | setNormRand |
| Return a scalar or array of arbitrary rank of random values from the standard univariate Normal distribution. More... | |
| interface | setNormRandBox |
| Return a scalar or array of arbitrary rank of random values from the univariate Normal distribution, using the Box-Muller algorithm. More... | |
Variables | |
| character(*, SK), parameter | MODULE_NAME = "@pm_distNorm" |
| integer(IK), parameter | ZIG_PRECISION = 33_IK |
The scalar integer of default kind IK containing the output of Fortran intrinsic precision() for the real kind used to generate the constant array ZIG_RKB.More... | |
| real(RKB), dimension(2, 0:128), parameter | ZIGSET1 = reshape([ +3.910757959524915869549621434510571640_RKB, +0.000000000000000000000000000000000000E+0_RKB , +3.654152885361008771645429720399515670_RKB, +0.502781343070952005087938400241541891E-3_RKB , +3.449278298561431270627228213833611250_RKB, +0.104086943106322506013635915064907845E-2_RKB , +3.320244733839825517532232984442230700_RKB, +0.161091799459473453538408742342021986E-2_RKB , +3.224575052047801587144019828764775500_RKB, +0.220312016549958827311372671027399889E-2_RKB , +3.147889289518000685451855194084413580_RKB, +0.281289233937616172611348633870502865E-2_RKB , +3.083526132002143251877768947617198840_RKB, +0.343751917929162224416229759239016324E-2_RKB , +3.027837791769593524571714584215607150_RKB, +0.407518400039001087464038448139061472E-2_RKB , +2.978603279881843165536974212294808030_RKB, +0.472457682607575925888895096351016103E-2_RKB , +2.934366867208887589959928979567677640_RKB, +0.538470372266379748395288853907771468E-2_RKB , +2.894121053613412181388100356210103800_RKB, +0.605478221942164063991037466747021604E-2_RKB , +2.857138730873224588561645268053226920_RKB, +0.673417886624137640800598237565554838E-2_RKB , +2.822877396826442907534115515646593530_RKB, +0.742236950888280249329920345563351449E-2_RKB , +2.790921174001927318997779045468293070_RKB, +0.811891273868296054077142626445965006E-2_RKB , +2.760944005279986201244382392492695240_RKB, +0.882343143223528339445647449425005264E-2_RKB , +2.732685359044011420043182513046678140_RKB, +0.953559949343287212693559957627379651E-2_RKB , +2.705933656123062221333700225998574460_RKB, +0.102551320707227866483396053794922990E-1_RKB , +2.680514643285745101098374611431323380_RKB, +0.109817781711791129427823736030159900E-1_RKB , +2.656283037576743296802124304559512000_RKB, +0.117153149732408013682731286377880085E-1_RKB , +2.633116393631582759976309292516893140_RKB, +0.124555433719091587849084452906815838E-1_RKB , +2.610910518488823671930263694478955450_RKB, +0.132022844366303809959357880408105012E-1_RKB , +2.589575986708286649808805574507900700_RKB, +0.139553765573260408177619288977468218E-1_RKB , +2.569035452681843781314262921528081910_RKB, +0.147146731176153334234423656007745630E-1_RKB , +2.549221550324783104422671371241746650_RKB, +0.154800405777112059806768992081788185E-1_RKB , +2.530075232159854187716539084126876370_RKB, +0.162513568797661774124156785927309438E-1_RKB , +2.511544441626694343254607344580084390_RKB, +0.170285101099635321775373808069033731E-1_RKB , +2.493583041271046768170053296506813290_RKB, +0.178113973671931254109163549358583312E-1_RKB , +2.476149939670523163756216268162166500_RKB, +0.185999237995485118944697972790344771E-1_RKB , +2.459208374334705035673859596487019180_RKB, +0.193940017783549904963609637793049119E-1_RKB , +2.442725318200364223794234919225453500_RKB, +0.201935501858165129428739457647187713E-1_RKB , +2.426670984937146719863529851633726960_RKB, +0.209984937972267218821328887239805004E-1_RKB , +2.411018413901119491690349211725038630_RKB, +0.218087627424279111659346610629834973E-1_RKB , +2.395743119781927356168686681412574760_RKB, +0.226242920341075527766680294896069533E-1_RKB , +2.380822795172085556506619691319380400_RKB, +0.234450211528013514383037474818822027E-1_RKB , +2.366237056717290911362148128140186000_RKB, +0.242708936802748765008871090362921378E-1_RKB , +2.351967227379144761902530751453964640_RKB, +0.251018569743934986305835005740321359E-1_RKB , +2.337996148796528635433480327093713940_RKB, +0.259378618797451777000075273655017443E-1_RKB , +2.324308018871132508266119157050790040_RKB, +0.267788624692146997471273278024758566E-1_RKB , +2.310888250601371758550614355860895420_RKB, +0.276248158124683715174543699462393572E-1_RKB , +2.297723348902863520079790814230529130_RKB, +0.284756817679310236840265332909329685E-1_RKB , +2.284800802724492127387834486937223350_RKB, +0.293314227953502809501556980682789090E-1_RKB , +2.272108990228381861937683717373910900_RKB, +0.301920037864680654091842729977054983E-1_RKB , +2.259637095173787624597566531167311770_RKB, +0.310573919116731481152577086508924965E-1_RKB , +2.247375032947389262297952392515659590_RKB, +0.319275564808046037696524061552362067E-1_RKB , +2.235313384929921110748362199673550240_RKB, +0.328024688165248443463852626030938600E-1_RKB , +2.223443340092510611365346409716922540_RKB, +0.336821021388909593274737975695380343E-1_RKB , +2.211756642884160997470500709266731210_RKB, +0.345664314599311541791934500133628777E-1_RKB , +2.200245546611276427712165173291835590_RKB, +0.354554334871846263278378901217329216E-1_RKB , +2.188902771626360742839576505604305880_RKB, +0.363490865352926868627480678085691155E-1_RKB , +2.177721467740293002579164079152503390_RKB, +0.372473704448399433976210004282028638E-1_RKB , +2.166695180354308542353137142121026540_RKB, +0.381502665077398667348211240367435477E-1_RKB , +2.155817819876737469119503677197502650_RKB, +0.390577573985415074098963321878992358E-1_RKB , +2.145083634047888982767999729572053870_RKB, +0.399698271111055203479683284323823695E-1_RKB , +2.134487182846016909178836604796243250_RKB, +0.408864609001596660576863760104051322E-1_RKB , +2.124023315689523545420714787478384860_RKB, +0.418076452272979751244992871255722388E-1_RKB , +2.113687150686653177781935198589005610_RKB, +0.427333677110349512002228670090424488E-1_RKB , +2.103474055714877305933714304045440450_RKB, +0.436636170805675209921984193602696278E-1_RKB , +2.093379631138791930166361585961667970_RKB, +0.445983831329337385181389634688869380E-1_RKB , +2.083399693998304613670792088175897210_RKB, +0.455376566932892082093887264381438529E-1_RKB , +2.073530263518743034646393248416971800_RKB, +0.464814295780503946152953311870656232E-1_RKB , +2.063767547811732114341853749078149630_RKB, +0.474296945606789346776298063351001244E-1_RKB , +2.054107931650652130219475666313816510_RKB, +0.483824453399031873773625284851490337E-1_RKB , +2.044547965217531455282628792749082960_RKB, +0.493396765101929088581344120097015200E-1_RKB , +2.035084353729618971413871948694988270_RKB, +0.503013835343204408492863489427518069E-1_RKB , +2.025713947863854245252399025955272060_RKB, +0.512675627178574145127079248497036520E-1_RKB , +2.016433734906204123873988577023278720_RKB, +0.522382111854699318500836298767666937E-1_RKB , +2.007240830560528758913239738198299090_RKB, +0.532133268588876922360496499106520185E-1_RKB , +1.998132471358419680392214769162858870_RKB, +0.541929084364337554633405727268610055E-1_RKB , +1.989106007617438123201023091217180910_RKB, +0.551769553740117250736639942272910314E-1_RKB , +1.980158896900476605540416694815765850_RKB, +0.561654678674562273820736142229565223E-1_RKB , +1.971288697933659294606356474434686550_RKB, +0.571584468361607664497222499802473837E-1_RKB , +1.962493064944363052826024381256974850_RKB, +0.581558939079044529261453899150298019E-1_RKB , +1.953769742384646776692572811817963060_RKB, +0.591578114048058224055549195846209505E-1_RKB , +1.945116560008678301234686281875394240_RKB, +0.601642023303380532839147151743642514E-1_RKB , +1.936531428275694700380702197135648770_RKB, +0.611750703573454323914419246868044098E-1_RKB , +1.928012334052665710328808957510011910_RKB, +0.621904198170059582295143354352838012E-1_RKB , +1.919557336593188113064282063465457130_RKB, +0.632102556886895688287062083850491706E-1_RKB , +1.911164563771253338349016119398665420_RKB, +0.642345835906656803805852580678544053E-1_RKB , +1.902832208550429269452784399230803680_RKB, +0.652634097716175649174146849378032930E-1_RKB , +1.894558525670704732040885690575958130_RKB, +0.662967411029246168483446165075442866E-1_RKB , +1.886341828536782820037856553309563160_RKB, +0.673345850716767915010299444811729445E-1_RKB , +1.878180486292995844684467996043645020_RKB, +0.683769497743884728203642791575539760E-1_RKB , +1.870072921071266778496337776290841830_RKB, +0.694238439113817677925134633773045847E-1_RKB , +1.862017605399674118665348784397922740_RKB, +0.704752767818117550133248257276187773E-1_RKB , +1.854013059760201906750898441184461490_RKB, +0.715312582793085547211649297744966411E-1_RKB , +1.846057850285185505570580952991448920_RKB, +0.725917988882132560598516526262197654E-1_RKB , +1.838150586582806633764931304898561700_RKB, +0.736569096803867509488343563799016629E-1_RKB , +1.830289919682756933756055676984081970_RKB, +0.747266023125723976798301015314803279E-1_RKB , +1.822474540093885838871898571617810260_RKB, +0.758008890242951847298446370142010715E-1_RKB , +1.814703175966282671680772343522476780_RKB, +0.768797826362816984781690401687711081E-1_RKB , +1.806974591350820938703420428388107530_RKB, +0.779632965493867285846698800079747914E-1_RKB , +1.799287584549720199341728680984235510_RKB, +0.790514447440137817496961412302243116E-1_RKB , +1.791640986552162594624382322132709310_RKB, +0.801442417800181275436054931177368005E-1_RKB , +1.784033659549441512971864077807943680_RKB, +0.812417027970822772687529532474258376E-1_RKB , +1.776464495524522868996124119276484200_RKB, +0.823438435155550059817881401744955979E-1_RKB , +1.768932414911268589029665159840958690_RKB, +0.834506802377461758021915029242417507E-1_RKB , +1.761436365318910280539794251593908460_RKB, +0.845622298496707118376316534786168010E-1_RKB , +1.753975320317671535176286495650271100_RKB, +0.856785098232361263350014624915617177E-1_RKB , +1.746548278281722412853610819915111290_RKB, +0.867995382188689874348253633476266673E-1_RKB , +1.739154261285911657262420055628115450_RKB, +0.879253336885766911833903717911534395E-1_RKB , +1.731792314052963154137933505808925000_RKB, +0.890559154794418239043567001488716945E-1_RKB , +1.724461502948044912052862397775662270_RKB, +0.901913034375473009991491331657262247E-1_RKB , +1.717160915017823089741659119609676780_RKB, +0.913315180123313418058911041645338441E-1_RKB , +1.709889657071301820241745482016102880_RKB, +0.924765802613721921296195811766027943E-1_RKB , +1.702646854799923151653900407051805770_RKB, +0.936265118556033400788781021199070560E-1_RKB , +1.695431651934561568299588089192625460_RKB, +0.947813350849607903374772538857282822E-1_RKB , +1.688243209437195389093695018261921410_RKB, +0.959410728644647702377950152378611650E-1_RKB , +1.681080704725173871909617303396002540_RKB, +0.971057487407390411201725488177809241E-1_RKB , +1.673943330926124999231911729230294350_RKB, +0.982753868989717834844303967803275557E-1_RKB , +1.666830296161665512280717200364773540_RKB, +0.994500121703228172933039137854161328E-1_RKB , +1.659740822858182552384789747414556960_RKB, +0.100629650039782712328127609576129162E+0_RKB , +1.652674147083055944977076666279072050_RKB, +0.101814326654490140522320621972065562E+0_RKB , +1.645629517904782346099997435068184430_RKB, +0.103004068832514625466733060901486566E+0_RKB , +1.638606196775547730191205373889528150_RKB, +0.104198904072112656528428960098709859E+0_RKB , +1.631603456934873546471532683464361160_RKB, +0.105398860561465958979782511482284346E+0_RKB , +1.624620582833034778354059455865975410_RKB, +0.106603967188911549935198869215607602E+0_RKB , +1.617656869573015532637880619762087450_RKB, +0.107814253553674065499513686193278908E+0_RKB , +1.610711622369830051160545249046193620_RKB, +0.109029749977111720145296612324748632E+0_RKB , +1.603784156026094530393066805218239570_RKB, +0.110250487514488157810061008578271138E+0_RKB , +1.596873794422788175563087978818873180_RKB, +0.111476497967283378462230486935475436E+0_RKB , +1.589979870024190797461111747861209560_RKB, +0.112707813896057876934855393386708534E+0_RKB , +1.583101723396029247521107058058590910_RKB, +0.113944468633885115777321981289805190E+0_RKB , +1.576238702735906320876658002975291310_RKB, +0.115186496300368473953376646626857215E+0_RKB , +1.569390163415123656042832370955675890_RKB, +0.116433931816259871778263682344311485E+0_RKB , +1.562555467531044820930627254229273630_RKB, +0.117686810918698373049736317381864947E+0_RKB , +1.555733983469176375991038619565492320_RKB, +0.118945170177088211568318678970235501E+0_RKB , +1.548925085474173406375274133330557850_RKB, +0.120209047009636885032310150781360772E+0_RKB , +1.542128153229001959318075945656599760_RKB, +0.121478479700575208713903649777558606E+0_RKB , +1.535342571441514138082707130216935300_RKB, +0.122753507418082528688239173356532507E+0_RKB ], shape = [2, 129]) |
| real(RKB), dimension(2, 1:128), parameter | ZIGSET2 = reshape([ +1.528567729437712402628199461442167180_RKB, +0.124034170232941664267186768442998377E+0_RKB , +1.521803020760998008679228498636570410_RKB, +0.125320509137949586535569901372920916E+0_RKB , +1.515047842776714566947194255734634790_RKB, +0.126612566068111349659514010876108850E+0_RKB , +1.508301596281311496171425183785073880_RKB, +0.127910383921646379432792471520964754E+0_RKB , +1.501563685115463738688173273682448190_RKB, +0.129214006581837895215365859576747957E+0_RKB , +1.494833515780493555035890159317754310_RKB, +0.130523478939758003270817270840923056E+0_RKB , +1.488110497057447553013103271226758760_RKB, +0.131838846917902858239534927650542548E+0_RKB , +1.481394039628187363902263028944763970_RKB, +0.133160157494774252287691074366070633E+0_RKB , +1.474683555697855570628865196528769660_RKB, +0.134487458730446066069814161355648980E+0_RKB , +1.467978458618079624962505551018572310_RKB, +0.135820799793156210330787895235534157E+0_RKB , +1.461278162510275558141634572902431380_RKB, +0.137160230986967010673991854114446593E+0_RKB , +1.454582081888410275202473614895370850_RKB, +0.138505803780539450342898439610712141E+0_RKB , +1.447889631280576100338960603208179050_RKB, +0.139857570837069297157912765350925466E+0_RKB , +1.441200224848723969896483905460819290_RKB, +0.141215586045435912189035654183361969E+0_RKB , +1.434513276005892200373197821347744230_RKB, +0.142579904552617481390538701477587025E+0_RKB , +1.427828197030256028046923580264626420_RKB, +0.143950582797429540314021584008091148E+0_RKB , +1.421144398675309048678328840045534000_RKB, +0.145327678545646990255525094264574683E+0_RKB , +1.414461289775471190729091975769526810_RKB, +0.146711250926573347052911625905291106E+0_RKB , +1.407778276846398829890729544114189010_RKB, +0.148101360471124737782233265331001140E+0_RKB , +1.401094763679250977372468027391928780_RKB, +0.149498069151500183758164830605819877E+0_RKB , +1.394410150928141013910818209046742880_RKB, +0.150901440422514000012107606564276651E+0_RKB , +1.387723835689976042816457610158740000_RKB, +0.152311539264670722976597120096621794E+0_RKB , +1.381035211075855426557023886048995030_RKB, +0.153728432229067872471998597962422358E+0_RKB , +1.374343665773166259809330405021183000_RKB, +0.155152187484217086331763054685730862E+0_RKB , +1.367648583597476202662733878746826080_RKB, +0.156582874864879763414378129073938725E+0_RKB , +1.360949343033283011396528844287145660_RKB, +0.158020565923019343095774015163019653E+0_RKB , +1.354245316762634995007843766072061330_RKB, +0.159465333980978769091659649295558937E+0_RKB , +1.347535871180587198226303191916842980_RKB, +0.160917254186998568094181273666041719E+0_RKB , +1.340820365896404038797740514363138740_RKB, +0.162376403573198357993539454690214112E+0_RKB , +1.334098153219360045667959181721837720_RKB, +0.163842861116152528813630294472766962E+0_RKB , +1.327368577627925853644432080219569470_RKB, +0.165316707800199358376684187822216740E+0_RKB , +1.320630975221056264316363281880977050_RKB, +0.166798026683631985045755192821871952E+0_RKB , +1.313884673150220489854736808952840970_RKB, +0.168286902967929517543098016930008494E+0_RKB , +1.307128989030731110178131195502915220_RKB, +0.169783424070197178160245257400787177E+0_RKB , +1.300363230330837190351929439655934200_RKB, +0.171287679698995818105358886788417999E+0_RKB , +1.293586693736947753945601406359300470_RKB, +0.172799761933753486486498659023686530E+0_RKB , +1.286798664493243646316660896517199420_RKB, +0.174319765307965059246455246546117697E+0_RKB , +1.279998415713817924797308907917922830_RKB, +0.175847786896400331371952020571991623E+0_RKB , +1.273185207665356364764060323720764170_RKB, +0.177383926406556544373322976411406151E+0_RKB , +1.266358287018229453775313848849852450_RKB, +0.178928286274608171283092549748417432E+0_RKB , +1.259516886063714228190559472001646690_RKB, +0.180480971766125034830178787412733260E+0_RKB , +1.252660221894897227354473865616388090_RKB, +0.182042091081849625639024292847696263E+0_RKB , +1.245787495548627294596662055366290760_RKB, +0.183611755468845965529740751119222664E+0_RKB , +1.238897891105687374493975672708951630_RKB, +0.185190079337355691907687938603429913E+0_RKB , +1.231990574746136091354596183983300960_RKB, +0.186777180383722406901836668848789685E+0_RKB , +1.225064693756530787096859391988721310_RKB, +0.188373179719772944131913560975705614E+0_RKB , +1.218119375485481656036492926236470550_RKB, +0.189978202009074284878057268848586717E+0_RKB , +1.211153726243699183035927701680494030_RKB, +0.191592375610517658429468812562799404E+0_RKB , +1.204166830144381512972585409228431810_RKB, +0.193215832729717172651871738633649002E+0_RKB , +1.197157747879441555149951169947666830_RKB, +0.194848709578749458096518050299059063E+0_RKB , +1.190125515426692069320479795685490130_RKB, +0.196491146544803628100426175257282935E+0_RKB , +1.183069142682686761029921497512774320_RKB, +0.198143288368357757303338740744073695E+0_RKB , +1.175987612015452098437940687032687740_RKB, +0.199805284331549509895377775340098004E+0_RKB , +1.168879876730833138384076802216189500_RKB, +0.201477288457465010601480272621186237E+0_RKB , +1.161744859445611442407678658730303350_RKB, +0.203159459721132113428367115004471988E+0_RKB , +1.154581450359927740740669252500180290_RKB, +0.204851962273072525723359017960643915E+0_RKB , +1.147388505420849058458757243582079270_RKB, +0.206554965676342511391397805599266881E+0_RKB , +1.140164844368151242664448937938463130_RKB, +0.208268645158074945659692042041697417E+0_RKB , +1.132909248652533753115898715892141530_RKB, +0.209993181876627252316799052585710853E+0_RKB , +1.125620459215533391227475593856507500_RKB, +0.211728763205541276296151308493989896E+0_RKB , +1.118297174119344981546693309349106980_RKB, +0.213475583035633628019879947303927958E+0_RKB , +1.110938046013575721417560779257849040_RKB, +0.215233842096659846410648766825208954E+0_RKB , +1.103541679424639718350709546845052450_RKB, +0.217003748300134423613077654918982009E+0_RKB , +1.096106627852021437094938365415991340_RKB, +0.218785517105043099072370007214575357E+0_RKB , +1.088631390653979821403993213445028160_RKB, +0.220579371908355906900178024260990122E+0_RKB , +1.081114409703403838077538136757234410_RKB, +0.222385544462441594762945169415386684E+0_RKB , +1.073554065792436288292686500464555760_RKB, +0.224204275321698924941276382479365999E+0_RKB , +1.065948674762122501754284026538321330_RKB, +0.226035814320961132564753113117134625E+0_RKB , +1.058296483330675084513966896229645790_RKB, +0.227880421088500051269826182271994471E+0_RKB , +1.050595664590929901514279329073961990_RKB, +0.229738365596760291802256320937473869E+0_RKB , +1.042844313144148970939980229020163640_RKB, +0.231609928754296215469589885980076311E+0_RKB , +1.035040439833440875887862746039381010_RKB, +0.233495403042770916853974440099008843E+0_RKB , +1.027181966035645772350639887939364020_RKB, +0.235395093203313594481836509609421923E+0_RKB , +1.019266717465484244962537467525869270_RKB, +0.237309316977027237519675921574483765E+0_RKB , +1.011292417439995739530489041191619980_RKB, +0.239238405905001516168070540916910782E+0_RKB , +1.003256679544672977063838476902952280_RKB, +0.241182706193826750302150947619295807E+0_RKB , +0.995156999635090923837912834290083799_RKB, +0.243142579653336370820347935962210089E+0_RKB , +0.986990747099062472368807733566367723_RKB, +0.245118404714142202924320107980890993E+0_RKB , +0.978755155294224603880824209605885949_RKB, +0.247110577533486783260721039414118216E+0_RKB , +0.970447311064224450680967868251783851_RKB, +0.249119513199040723215271175059742679E+0_RKB , +0.962064143223040583869351754884239000_RKB, +0.251145647041545878684196026994747375E+0_RKB , +0.953602409881086036147944393710646946_RKB, +0.253189436068676791163884011564958290E+0_RKB , +0.945058684468165463037907528952905452_RKB, +0.255251360534199633721355034811644515E+0_RKB , +0.936429340286575141234349646203595494_RKB, +0.257331925658493337610224432667231202E+0_RKB , +0.927710533402000123870677193352685174_RKB, +0.259431663518814566212074318832185428E+0_RKB , +0.918898183649590612180034442455129809_RKB, +0.261551135130401113878336401593219032E+0_RKB , +0.909987953496718494483529567690366580_RKB, +0.263690932742695838070411741690697980E+0_RKB , +0.900975224461221833746547856386022859_RKB, +0.265851682378732029260877257163356597E+0_RKB , +0.891855070732941566850586789359498648_RKB, +0.268034046650170417793435080776528378E+0_RKB , +0.882622229585165554772936671621819385_RKB, +0.270238727885765625479222906930855857E+0_RKB , +0.873271068088860754125762716220304264_RKB, +0.272466471617349972495381721975295691E+0_RKB , +0.863795545553308854813178505394360638_RKB, +0.274718070474985863152207934163143218E+0_RKB , +0.854189171008163807454180162989399104_RKB, +0.276994368552045124993231875042116081E+0_RKB , +0.844444954909153918889582440732428571_RKB, +0.279296266311992916126496729438627603E+0_RKB , +0.834555354086382178924726895193815695_RKB, +0.281624726122054644081592741705012005E+0_RKB , +0.824512208752292130518310689451625822_RKB, +0.283980778515329245279710753274268026E+0_RKB , +0.814306670135215230392694899997583155_RKB, +0.286365529303059635938328101021065686E+0_RKB , +0.803929116989971220407539518038181495_RKB, +0.288780167683694362995818015176624321E+0_RKB , +0.793369058840623296211094246674767659_RKB, +0.291225975526402318340687192537257840E+0_RKB , +0.782615023307233120893558043746138323_RKB, +0.293704338045591948359518681668325255E+0_RKB , +0.771654424224568084749572873233895398_RKB, +0.296216756132081268041022602880704688E+0_RKB , +0.760473406430108029348112105521972518_RKB, +0.298764860669019852359816171738518807E+0_RKB , +0.749056662017815292302576863549466866_RKB, +0.301350429240767224099410447613497339E+0_RKB , +0.737387211434295591278302895320305406_RKB, +0.303975405746574722328106158035369533E+0_RKB , +0.725446140909999639160421404681071701_RKB, +0.306641923566284096197801960631070354E+0_RKB , +0.713212285190975958395437234225351400_RKB, +0.309352333103853461802712328689370145E+0_RKB , +0.700661841106815072627797458756938969_RKB, +0.312109234772742761743862339129657007E+0_RKB , +0.687767892795788534294858623414951669_RKB, +0.314915518808718397997156048518493503E+0_RKB , +0.674499822837293822822291441953147501_RKB, +0.317774413735206587646816278462680542E+0_RKB , +0.660822574244419738417074112845703024_RKB, +0.320689545915737438541580666581786760E+0_RKB , +0.646695714894993817513389454402005337_RKB, +0.323665013485929872609853214812546138E+0_RKB , +0.632072236386061170945000136838048409_RKB, +0.326705479185682685503639905197287285E+0_RKB , +0.616896990007751449983468424580333684_RKB, +0.329816288403562001297942710464242773E+0_RKB , +0.601104617755992621533900682881952269_RKB, +0.333003621412417574590814956444079152E+0_RKB , +0.584616766106379321441587601292714165_RKB, +0.336274692838645610198728629890296241E+0_RKB , +0.567338257053818748196811566000406618_RKB, +0.339638017760732372141674530066184563E+0_RKB , +0.549151702327165120668100504067842453_RKB, +0.343103774061966311836681659618112095E+0_RKB , +0.529909720661558116786810165407173123_RKB, +0.346684307694080825876172229626686798E+0_RKB , +0.509423329602091814469823299066412422_RKB, +0.350394856987006815154163453112784578E+0_RKB , +0.487443966139236039301073245095571196_RKB, +0.354254625523424624005573055746854654E+0_RKB , +0.463634336790882217507922976793371502_RKB, +0.358288435101351989902170775658332694E+0_RKB , +0.437518402207871681933515025173607280_RKB, +0.362529398255472763687561092414814622E+0_RKB , +0.408389134611991145290558016416221589_RKB, +0.367023508970343116977068094647372845E+0_RKB , +0.375121332878380591495093443929722987_RKB, +0.371838172174307847618293715165674310E+0_RKB , +0.335737519214425235638195399148542308_RKB, +0.377079825919318504715611620323180171E+0_RKB , +0.286174591792072510002201653739714122_RKB, +0.382936353792390580381634933484297406E+0_RKB , +0.215241895984881699325976137068393403_RKB, +0.389807180887844207493515693365586429E+0_RKB , +0.000000000000000000000000000000000000_RKB, +0.398942280401432677939946059934381874E+0_RKB ], shape = [2, 128]) |
| real(RKB), dimension(2, 0:256), parameter | ZIG_RKB = reshape([ZIGSET1, ZIGSET2], shape = [2, 257]) |
The constant array of type real of kind RKB of shape (1 : 2, 0 : 256) containing the default 256-layers Ziggurat set information that is used within setNormRand to generate standard Normal random numbers.More... | |
This module contains classes and procedures for computing various statistical quantities related to the univariate Normal distribution.
Specifically, this module contains routines for computing the following quantities of the univariate Normal distribution:
The PDF of the Normal distribution is defined with the two location and scale parameters (\mu \in (-\infty, +\infty), \sigma > 0) as,
\begin{equation} \large \pi(x | \mu, \sigma) = \frac{1}{\sigma\sqrt{2\pi}}\exp\bigg( -\frac{\big(x - \mu\big)^2}{2\sigma^2} \bigg) ~,~ x \in (-\infty, +\infty) ~. \end{equation}
The CDF of the Normal distribution is defined with the two location and scale parameters (\mu \in (-\infty, +\infty), \sigma > 0) as,
\begin{equation} \large \mathrm{CDF}(x | \mu, \sigma) = \frac{1}{2} \bigg[ 1 + \mathrm{erf} \bigg( \frac{x - \mu}{\sigma\sqrt{2}} \bigg) \bigg] ~,~ x \in (-\infty, +\infty) ~. \end{equation}
Quantile Function
In probability and statistics, the quantile function outputs the value of a random variable such that its probability is less than or equal to an input probability value.
Intuitively, the quantile function associates with a range at and below a probability input the likelihood that a random variable is realized in that range for some probability distribution.
It is also called the percentile function, percent-point function or inverse cumulative distribution function (ICDF).
See the documentation of pm_distNorm for information on the CDF of the Normal distribution.
The quantile function of the standard normal distribution is called the probit function, and can be expressed in terms of the inverse error function:
\begin{equation} \Phi^{-1}(p) = {\sqrt{2}}\ms{erf}^{-1}(2p - 1), \quad p \in (0,1) ~. \end{equation}
For a normal random variable with mean \mu and variance \sigma^{2}, the quantile function is,
\begin{equation} F^{-1}(p) = \mu + \sigma \Phi^{-1}(p) = \mu + \sigma \sqrt{2} \ms{erf}^{-1}(2p - 1), \quad p \in (0,1) ~. \end{equation}
The quantile \Phi^{-1}(p) of the standard normal distribution is commonly denoted as z_{p}.
These values are used in hypothesis testing, construction of confidence intervals and Q–Q plots.
A normal random variable X will exceed \mu + z_{p}\sigma with probability 1 − p, and will lie outside the interval \mu \pm z_{p} \sigma with probability 2(1 - p).
In particular, the quantile z_{0.975} is 1.96.
Therefore a normal random variable will lie outside the interval \mu \pm 1.96\sigma in only 5\% of cases.
The following table gives the quantile z_{p} such that X will lie in the range \mu \pm z_{p}\sigma with a specified probability p.
These values are useful to determine tolerance interval for sample averages and other statistical estimators with normal (or asymptotically normal) distributions.
Note that the following table shows \sqrt{2} \ms{erf}^{-1}(p) = \Phi^{-1}\left(\frac{p + 1}{2}\right), not \Phi^{-1}(p) as defined above.
| p | z_{p} |
|---|---|
| 0.80 | 1.281551565545 |
| 0.90 | 1.644853626951 |
| 0.95 | 1.959963984540 |
| 0.98 | 2.326347874041 |
| 0.99 | 2.575829303549 |
| 0.995 | 2.807033768344 |
| 0.998 | 3.090232306168 |
| 0.999 | 3.290526731492 |
| 0.9999 | 3.890591886413 |
| 0.99999 | 4.417173413469 |
| 0.999999 | 4.891638475699 |
| 0.9999999 | 5.326723886384 |
| 0.99999999 | 5.730728868236 |
| 0.999999999 | 6.109410204869 |
For small p, the quantile function has the useful asymptotic expansion \Phi^{-1}(p) = -\sqrt{\ln{\frac{1}{p^{2}}} - \ln\ln{\frac{1}{p^{2}}} - \ln(2\pi)} + \mathcal{o}(1).
Random Number Generation
The current implementations of the RNG generic interfaces of this module use the Box-Muller trigonometric and rejection methods for Normal random number generation.
real32 Standard Normal random numbers generated by the Box-Muller algorithm are known to be limited to the range [-6.66, +6.66].real64 Standard Normal random numbers generated by the Box-Muller algorithm are known to be limited to the range [-9.419, +9.419].The entropy of the Normal distribution is defined by the following equation,
\begin{equation} \large \mathcal{H}(\sigma^2) = \frac{1}{2} \log(2\pi\sigma^2) + \frac{1}{2} \end{equation}
Fisher Information
The Fisher information for the Normal distribution is defined by the following equation,
\begin{equation} \large \mathcal{I}(\mu,\sigma) = \begin{pmatrix} \frac{1}{\sigma^2} & 0 \\ 0 & \frac{2}{\sigma^2} \\ \end{pmatrix} \end{equation}
Kullback-Leibler Divergence (KLD)
The Kullback-Leibler Divergence, also known as the relative entropy, of a univariate Normal distribution Q from a reference univariate Normal distribution P is defined as,
\begin{equation} \large D_{KL}(P \parallel Q) = \frac{(\mu_P - \mu_Q)^2}{2\sigma_Q^2} + \frac{1}{2}\bigg( \frac{\sigma_P}{\sigma_Q} - \ln\big(\frac{\sigma_P}{\sigma_Q}\big) - 1 \bigg) ~, \end{equation}
Benchmark :: The runtime performance of setNormRand and setNormRandBox. ⛓
ifort compiler ⛓ ifort compiler ⛓ gfortran compiler ⛓ 
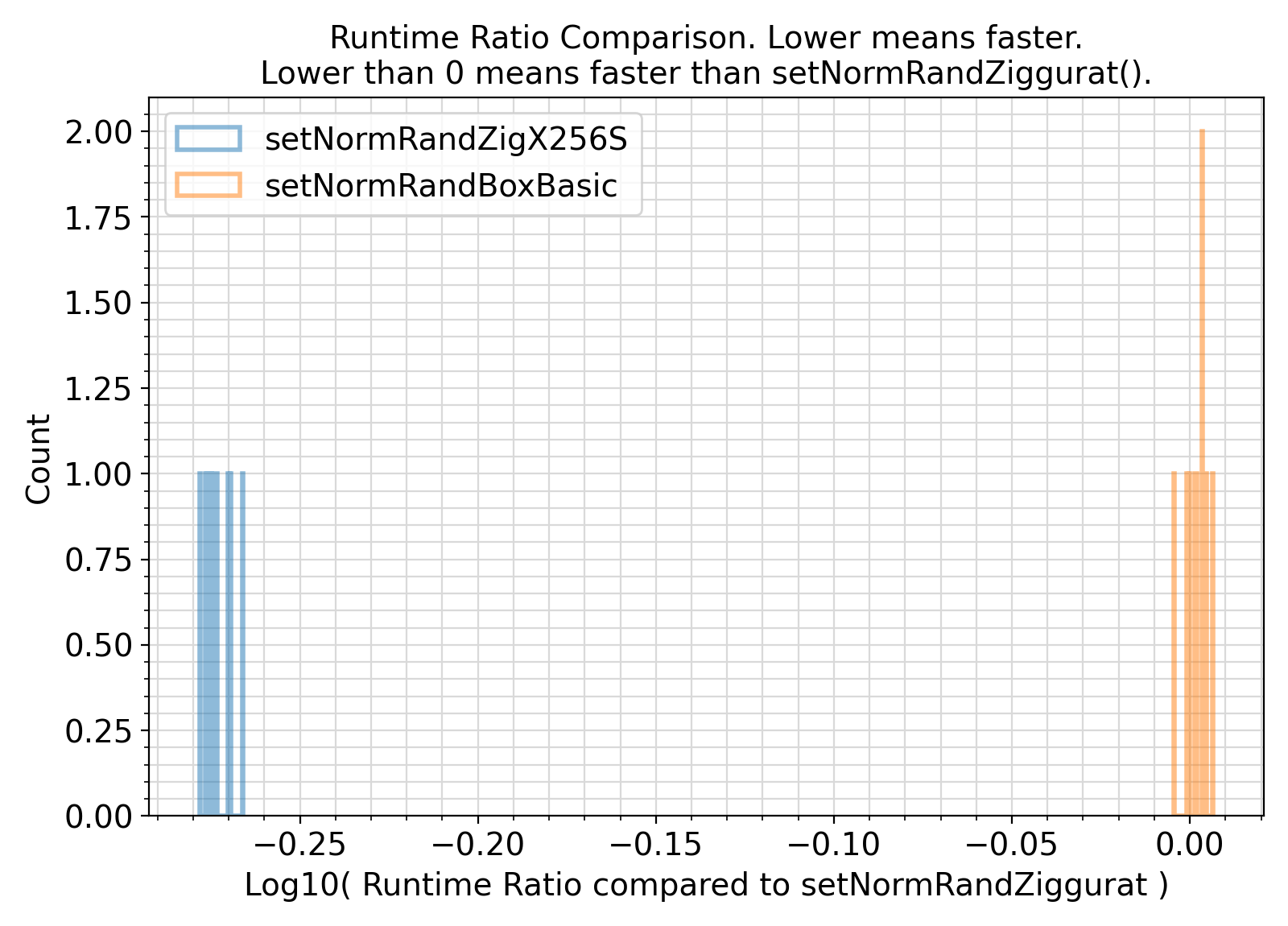
setNormRandZiggurat and setNormRandBoxBasic call the generic interfaces setNormRand (ziggurat method) and setNormRandBox (basic trigonometric Box-Muller method) respectively.setNormRandZigX256S calls the generic interface setNormRand with the xoshiro256ssw_type RNG instead of the default intrinsic Fortran RNG.impure when the default intrinsic Fortran RNG is used.real kind.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
| character(*, SK), parameter pm_distNorm::MODULE_NAME = "@pm_distNorm" |
Definition at line 187 of file pm_distNorm.F90.
| integer(IK), parameter pm_distNorm::ZIG_PRECISION = 33_IK |
The scalar integer of default kind IK containing the output of Fortran intrinsic precision() for the real kind used to generate the constant array ZIG_RKB.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1487 of file pm_distNorm.F90.
| real(RKB), dimension(2, 0:256), parameter pm_distNorm::ZIG_RKB = reshape([ZIGSET1, ZIGSET2], shape = [2, 257]) |
The constant array of type real of kind RKB of shape (1 : 2, 0 : 256) containing the default 256-layers Ziggurat set information that is used within setNormRand to generate standard Normal random numbers.
The subset ZIG_RKB(1, :) corresponding to the lower right corners of the 256 Ziggurat rectangles are computed via getZigNorm yielding a maximum absolute error abserr = +0.562732655625645475814793555099033451E-33 in the rectangle areas.
amd64 processor with the highest machine precision available for real type, yielding a maximum of ZIG_PRECISION digits of precision.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1774 of file pm_distNorm.F90.
| real(RKB), dimension(2, 0:128), parameter pm_distNorm::ZIGSET1 = reshape([ +3.910757959524915869549621434510571640_RKB, +0.000000000000000000000000000000000000E+0_RKB , +3.654152885361008771645429720399515670_RKB, +0.502781343070952005087938400241541891E-3_RKB , +3.449278298561431270627228213833611250_RKB, +0.104086943106322506013635915064907845E-2_RKB , +3.320244733839825517532232984442230700_RKB, +0.161091799459473453538408742342021986E-2_RKB , +3.224575052047801587144019828764775500_RKB, +0.220312016549958827311372671027399889E-2_RKB , +3.147889289518000685451855194084413580_RKB, +0.281289233937616172611348633870502865E-2_RKB , +3.083526132002143251877768947617198840_RKB, +0.343751917929162224416229759239016324E-2_RKB , +3.027837791769593524571714584215607150_RKB, +0.407518400039001087464038448139061472E-2_RKB , +2.978603279881843165536974212294808030_RKB, +0.472457682607575925888895096351016103E-2_RKB , +2.934366867208887589959928979567677640_RKB, +0.538470372266379748395288853907771468E-2_RKB , +2.894121053613412181388100356210103800_RKB, +0.605478221942164063991037466747021604E-2_RKB , +2.857138730873224588561645268053226920_RKB, +0.673417886624137640800598237565554838E-2_RKB , +2.822877396826442907534115515646593530_RKB, +0.742236950888280249329920345563351449E-2_RKB , +2.790921174001927318997779045468293070_RKB, +0.811891273868296054077142626445965006E-2_RKB , +2.760944005279986201244382392492695240_RKB, +0.882343143223528339445647449425005264E-2_RKB , +2.732685359044011420043182513046678140_RKB, +0.953559949343287212693559957627379651E-2_RKB , +2.705933656123062221333700225998574460_RKB, +0.102551320707227866483396053794922990E-1_RKB , +2.680514643285745101098374611431323380_RKB, +0.109817781711791129427823736030159900E-1_RKB , +2.656283037576743296802124304559512000_RKB, +0.117153149732408013682731286377880085E-1_RKB , +2.633116393631582759976309292516893140_RKB, +0.124555433719091587849084452906815838E-1_RKB , +2.610910518488823671930263694478955450_RKB, +0.132022844366303809959357880408105012E-1_RKB , +2.589575986708286649808805574507900700_RKB, +0.139553765573260408177619288977468218E-1_RKB , +2.569035452681843781314262921528081910_RKB, +0.147146731176153334234423656007745630E-1_RKB , +2.549221550324783104422671371241746650_RKB, +0.154800405777112059806768992081788185E-1_RKB , +2.530075232159854187716539084126876370_RKB, +0.162513568797661774124156785927309438E-1_RKB , +2.511544441626694343254607344580084390_RKB, +0.170285101099635321775373808069033731E-1_RKB , +2.493583041271046768170053296506813290_RKB, +0.178113973671931254109163549358583312E-1_RKB , +2.476149939670523163756216268162166500_RKB, +0.185999237995485118944697972790344771E-1_RKB , +2.459208374334705035673859596487019180_RKB, +0.193940017783549904963609637793049119E-1_RKB , +2.442725318200364223794234919225453500_RKB, +0.201935501858165129428739457647187713E-1_RKB , +2.426670984937146719863529851633726960_RKB, +0.209984937972267218821328887239805004E-1_RKB , +2.411018413901119491690349211725038630_RKB, +0.218087627424279111659346610629834973E-1_RKB , +2.395743119781927356168686681412574760_RKB, +0.226242920341075527766680294896069533E-1_RKB , +2.380822795172085556506619691319380400_RKB, +0.234450211528013514383037474818822027E-1_RKB , +2.366237056717290911362148128140186000_RKB, +0.242708936802748765008871090362921378E-1_RKB , +2.351967227379144761902530751453964640_RKB, +0.251018569743934986305835005740321359E-1_RKB , +2.337996148796528635433480327093713940_RKB, +0.259378618797451777000075273655017443E-1_RKB , +2.324308018871132508266119157050790040_RKB, +0.267788624692146997471273278024758566E-1_RKB , +2.310888250601371758550614355860895420_RKB, +0.276248158124683715174543699462393572E-1_RKB , +2.297723348902863520079790814230529130_RKB, +0.284756817679310236840265332909329685E-1_RKB , +2.284800802724492127387834486937223350_RKB, +0.293314227953502809501556980682789090E-1_RKB , +2.272108990228381861937683717373910900_RKB, +0.301920037864680654091842729977054983E-1_RKB , +2.259637095173787624597566531167311770_RKB, +0.310573919116731481152577086508924965E-1_RKB , +2.247375032947389262297952392515659590_RKB, +0.319275564808046037696524061552362067E-1_RKB , +2.235313384929921110748362199673550240_RKB, +0.328024688165248443463852626030938600E-1_RKB , +2.223443340092510611365346409716922540_RKB, +0.336821021388909593274737975695380343E-1_RKB , +2.211756642884160997470500709266731210_RKB, +0.345664314599311541791934500133628777E-1_RKB , +2.200245546611276427712165173291835590_RKB, +0.354554334871846263278378901217329216E-1_RKB , +2.188902771626360742839576505604305880_RKB, +0.363490865352926868627480678085691155E-1_RKB , +2.177721467740293002579164079152503390_RKB, +0.372473704448399433976210004282028638E-1_RKB , +2.166695180354308542353137142121026540_RKB, +0.381502665077398667348211240367435477E-1_RKB , +2.155817819876737469119503677197502650_RKB, +0.390577573985415074098963321878992358E-1_RKB , +2.145083634047888982767999729572053870_RKB, +0.399698271111055203479683284323823695E-1_RKB , +2.134487182846016909178836604796243250_RKB, +0.408864609001596660576863760104051322E-1_RKB , +2.124023315689523545420714787478384860_RKB, +0.418076452272979751244992871255722388E-1_RKB , +2.113687150686653177781935198589005610_RKB, +0.427333677110349512002228670090424488E-1_RKB , +2.103474055714877305933714304045440450_RKB, +0.436636170805675209921984193602696278E-1_RKB , +2.093379631138791930166361585961667970_RKB, +0.445983831329337385181389634688869380E-1_RKB , +2.083399693998304613670792088175897210_RKB, +0.455376566932892082093887264381438529E-1_RKB , +2.073530263518743034646393248416971800_RKB, +0.464814295780503946152953311870656232E-1_RKB , +2.063767547811732114341853749078149630_RKB, +0.474296945606789346776298063351001244E-1_RKB , +2.054107931650652130219475666313816510_RKB, +0.483824453399031873773625284851490337E-1_RKB , +2.044547965217531455282628792749082960_RKB, +0.493396765101929088581344120097015200E-1_RKB , +2.035084353729618971413871948694988270_RKB, +0.503013835343204408492863489427518069E-1_RKB , +2.025713947863854245252399025955272060_RKB, +0.512675627178574145127079248497036520E-1_RKB , +2.016433734906204123873988577023278720_RKB, +0.522382111854699318500836298767666937E-1_RKB , +2.007240830560528758913239738198299090_RKB, +0.532133268588876922360496499106520185E-1_RKB , +1.998132471358419680392214769162858870_RKB, +0.541929084364337554633405727268610055E-1_RKB , +1.989106007617438123201023091217180910_RKB, +0.551769553740117250736639942272910314E-1_RKB , +1.980158896900476605540416694815765850_RKB, +0.561654678674562273820736142229565223E-1_RKB , +1.971288697933659294606356474434686550_RKB, +0.571584468361607664497222499802473837E-1_RKB , +1.962493064944363052826024381256974850_RKB, +0.581558939079044529261453899150298019E-1_RKB , +1.953769742384646776692572811817963060_RKB, +0.591578114048058224055549195846209505E-1_RKB , +1.945116560008678301234686281875394240_RKB, +0.601642023303380532839147151743642514E-1_RKB , +1.936531428275694700380702197135648770_RKB, +0.611750703573454323914419246868044098E-1_RKB , +1.928012334052665710328808957510011910_RKB, +0.621904198170059582295143354352838012E-1_RKB , +1.919557336593188113064282063465457130_RKB, +0.632102556886895688287062083850491706E-1_RKB , +1.911164563771253338349016119398665420_RKB, +0.642345835906656803805852580678544053E-1_RKB , +1.902832208550429269452784399230803680_RKB, +0.652634097716175649174146849378032930E-1_RKB , +1.894558525670704732040885690575958130_RKB, +0.662967411029246168483446165075442866E-1_RKB , +1.886341828536782820037856553309563160_RKB, +0.673345850716767915010299444811729445E-1_RKB , +1.878180486292995844684467996043645020_RKB, +0.683769497743884728203642791575539760E-1_RKB , +1.870072921071266778496337776290841830_RKB, +0.694238439113817677925134633773045847E-1_RKB , +1.862017605399674118665348784397922740_RKB, +0.704752767818117550133248257276187773E-1_RKB , +1.854013059760201906750898441184461490_RKB, +0.715312582793085547211649297744966411E-1_RKB , +1.846057850285185505570580952991448920_RKB, +0.725917988882132560598516526262197654E-1_RKB , +1.838150586582806633764931304898561700_RKB, +0.736569096803867509488343563799016629E-1_RKB , +1.830289919682756933756055676984081970_RKB, +0.747266023125723976798301015314803279E-1_RKB , +1.822474540093885838871898571617810260_RKB, +0.758008890242951847298446370142010715E-1_RKB , +1.814703175966282671680772343522476780_RKB, +0.768797826362816984781690401687711081E-1_RKB , +1.806974591350820938703420428388107530_RKB, +0.779632965493867285846698800079747914E-1_RKB , +1.799287584549720199341728680984235510_RKB, +0.790514447440137817496961412302243116E-1_RKB , +1.791640986552162594624382322132709310_RKB, +0.801442417800181275436054931177368005E-1_RKB , +1.784033659549441512971864077807943680_RKB, +0.812417027970822772687529532474258376E-1_RKB , +1.776464495524522868996124119276484200_RKB, +0.823438435155550059817881401744955979E-1_RKB , +1.768932414911268589029665159840958690_RKB, +0.834506802377461758021915029242417507E-1_RKB , +1.761436365318910280539794251593908460_RKB, +0.845622298496707118376316534786168010E-1_RKB , +1.753975320317671535176286495650271100_RKB, +0.856785098232361263350014624915617177E-1_RKB , +1.746548278281722412853610819915111290_RKB, +0.867995382188689874348253633476266673E-1_RKB , +1.739154261285911657262420055628115450_RKB, +0.879253336885766911833903717911534395E-1_RKB , +1.731792314052963154137933505808925000_RKB, +0.890559154794418239043567001488716945E-1_RKB , +1.724461502948044912052862397775662270_RKB, +0.901913034375473009991491331657262247E-1_RKB , +1.717160915017823089741659119609676780_RKB, +0.913315180123313418058911041645338441E-1_RKB , +1.709889657071301820241745482016102880_RKB, +0.924765802613721921296195811766027943E-1_RKB , +1.702646854799923151653900407051805770_RKB, +0.936265118556033400788781021199070560E-1_RKB , +1.695431651934561568299588089192625460_RKB, +0.947813350849607903374772538857282822E-1_RKB , +1.688243209437195389093695018261921410_RKB, +0.959410728644647702377950152378611650E-1_RKB , +1.681080704725173871909617303396002540_RKB, +0.971057487407390411201725488177809241E-1_RKB , +1.673943330926124999231911729230294350_RKB, +0.982753868989717834844303967803275557E-1_RKB , +1.666830296161665512280717200364773540_RKB, +0.994500121703228172933039137854161328E-1_RKB , +1.659740822858182552384789747414556960_RKB, +0.100629650039782712328127609576129162E+0_RKB , +1.652674147083055944977076666279072050_RKB, +0.101814326654490140522320621972065562E+0_RKB , +1.645629517904782346099997435068184430_RKB, +0.103004068832514625466733060901486566E+0_RKB , +1.638606196775547730191205373889528150_RKB, +0.104198904072112656528428960098709859E+0_RKB , +1.631603456934873546471532683464361160_RKB, +0.105398860561465958979782511482284346E+0_RKB , +1.624620582833034778354059455865975410_RKB, +0.106603967188911549935198869215607602E+0_RKB , +1.617656869573015532637880619762087450_RKB, +0.107814253553674065499513686193278908E+0_RKB , +1.610711622369830051160545249046193620_RKB, +0.109029749977111720145296612324748632E+0_RKB , +1.603784156026094530393066805218239570_RKB, +0.110250487514488157810061008578271138E+0_RKB , +1.596873794422788175563087978818873180_RKB, +0.111476497967283378462230486935475436E+0_RKB , +1.589979870024190797461111747861209560_RKB, +0.112707813896057876934855393386708534E+0_RKB , +1.583101723396029247521107058058590910_RKB, +0.113944468633885115777321981289805190E+0_RKB , +1.576238702735906320876658002975291310_RKB, +0.115186496300368473953376646626857215E+0_RKB , +1.569390163415123656042832370955675890_RKB, +0.116433931816259871778263682344311485E+0_RKB , +1.562555467531044820930627254229273630_RKB, +0.117686810918698373049736317381864947E+0_RKB , +1.555733983469176375991038619565492320_RKB, +0.118945170177088211568318678970235501E+0_RKB , +1.548925085474173406375274133330557850_RKB, +0.120209047009636885032310150781360772E+0_RKB , +1.542128153229001959318075945656599760_RKB, +0.121478479700575208713903649777558606E+0_RKB , +1.535342571441514138082707130216935300_RKB, +0.122753507418082528688239173356532507E+0_RKB ], shape = [2, 129]) |
Definition at line 1489 of file pm_distNorm.F90.
| real(RKB), dimension(2, 1:128), parameter pm_distNorm::ZIGSET2 = reshape([ +1.528567729437712402628199461442167180_RKB, +0.124034170232941664267186768442998377E+0_RKB , +1.521803020760998008679228498636570410_RKB, +0.125320509137949586535569901372920916E+0_RKB , +1.515047842776714566947194255734634790_RKB, +0.126612566068111349659514010876108850E+0_RKB , +1.508301596281311496171425183785073880_RKB, +0.127910383921646379432792471520964754E+0_RKB , +1.501563685115463738688173273682448190_RKB, +0.129214006581837895215365859576747957E+0_RKB , +1.494833515780493555035890159317754310_RKB, +0.130523478939758003270817270840923056E+0_RKB , +1.488110497057447553013103271226758760_RKB, +0.131838846917902858239534927650542548E+0_RKB , +1.481394039628187363902263028944763970_RKB, +0.133160157494774252287691074366070633E+0_RKB , +1.474683555697855570628865196528769660_RKB, +0.134487458730446066069814161355648980E+0_RKB , +1.467978458618079624962505551018572310_RKB, +0.135820799793156210330787895235534157E+0_RKB , +1.461278162510275558141634572902431380_RKB, +0.137160230986967010673991854114446593E+0_RKB , +1.454582081888410275202473614895370850_RKB, +0.138505803780539450342898439610712141E+0_RKB , +1.447889631280576100338960603208179050_RKB, +0.139857570837069297157912765350925466E+0_RKB , +1.441200224848723969896483905460819290_RKB, +0.141215586045435912189035654183361969E+0_RKB , +1.434513276005892200373197821347744230_RKB, +0.142579904552617481390538701477587025E+0_RKB , +1.427828197030256028046923580264626420_RKB, +0.143950582797429540314021584008091148E+0_RKB , +1.421144398675309048678328840045534000_RKB, +0.145327678545646990255525094264574683E+0_RKB , +1.414461289775471190729091975769526810_RKB, +0.146711250926573347052911625905291106E+0_RKB , +1.407778276846398829890729544114189010_RKB, +0.148101360471124737782233265331001140E+0_RKB , +1.401094763679250977372468027391928780_RKB, +0.149498069151500183758164830605819877E+0_RKB , +1.394410150928141013910818209046742880_RKB, +0.150901440422514000012107606564276651E+0_RKB , +1.387723835689976042816457610158740000_RKB, +0.152311539264670722976597120096621794E+0_RKB , +1.381035211075855426557023886048995030_RKB, +0.153728432229067872471998597962422358E+0_RKB , +1.374343665773166259809330405021183000_RKB, +0.155152187484217086331763054685730862E+0_RKB , +1.367648583597476202662733878746826080_RKB, +0.156582874864879763414378129073938725E+0_RKB , +1.360949343033283011396528844287145660_RKB, +0.158020565923019343095774015163019653E+0_RKB , +1.354245316762634995007843766072061330_RKB, +0.159465333980978769091659649295558937E+0_RKB , +1.347535871180587198226303191916842980_RKB, +0.160917254186998568094181273666041719E+0_RKB , +1.340820365896404038797740514363138740_RKB, +0.162376403573198357993539454690214112E+0_RKB , +1.334098153219360045667959181721837720_RKB, +0.163842861116152528813630294472766962E+0_RKB , +1.327368577627925853644432080219569470_RKB, +0.165316707800199358376684187822216740E+0_RKB , +1.320630975221056264316363281880977050_RKB, +0.166798026683631985045755192821871952E+0_RKB , +1.313884673150220489854736808952840970_RKB, +0.168286902967929517543098016930008494E+0_RKB , +1.307128989030731110178131195502915220_RKB, +0.169783424070197178160245257400787177E+0_RKB , +1.300363230330837190351929439655934200_RKB, +0.171287679698995818105358886788417999E+0_RKB , +1.293586693736947753945601406359300470_RKB, +0.172799761933753486486498659023686530E+0_RKB , +1.286798664493243646316660896517199420_RKB, +0.174319765307965059246455246546117697E+0_RKB , +1.279998415713817924797308907917922830_RKB, +0.175847786896400331371952020571991623E+0_RKB , +1.273185207665356364764060323720764170_RKB, +0.177383926406556544373322976411406151E+0_RKB , +1.266358287018229453775313848849852450_RKB, +0.178928286274608171283092549748417432E+0_RKB , +1.259516886063714228190559472001646690_RKB, +0.180480971766125034830178787412733260E+0_RKB , +1.252660221894897227354473865616388090_RKB, +0.182042091081849625639024292847696263E+0_RKB , +1.245787495548627294596662055366290760_RKB, +0.183611755468845965529740751119222664E+0_RKB , +1.238897891105687374493975672708951630_RKB, +0.185190079337355691907687938603429913E+0_RKB , +1.231990574746136091354596183983300960_RKB, +0.186777180383722406901836668848789685E+0_RKB , +1.225064693756530787096859391988721310_RKB, +0.188373179719772944131913560975705614E+0_RKB , +1.218119375485481656036492926236470550_RKB, +0.189978202009074284878057268848586717E+0_RKB , +1.211153726243699183035927701680494030_RKB, +0.191592375610517658429468812562799404E+0_RKB , +1.204166830144381512972585409228431810_RKB, +0.193215832729717172651871738633649002E+0_RKB , +1.197157747879441555149951169947666830_RKB, +0.194848709578749458096518050299059063E+0_RKB , +1.190125515426692069320479795685490130_RKB, +0.196491146544803628100426175257282935E+0_RKB , +1.183069142682686761029921497512774320_RKB, +0.198143288368357757303338740744073695E+0_RKB , +1.175987612015452098437940687032687740_RKB, +0.199805284331549509895377775340098004E+0_RKB , +1.168879876730833138384076802216189500_RKB, +0.201477288457465010601480272621186237E+0_RKB , +1.161744859445611442407678658730303350_RKB, +0.203159459721132113428367115004471988E+0_RKB , +1.154581450359927740740669252500180290_RKB, +0.204851962273072525723359017960643915E+0_RKB , +1.147388505420849058458757243582079270_RKB, +0.206554965676342511391397805599266881E+0_RKB , +1.140164844368151242664448937938463130_RKB, +0.208268645158074945659692042041697417E+0_RKB , +1.132909248652533753115898715892141530_RKB, +0.209993181876627252316799052585710853E+0_RKB , +1.125620459215533391227475593856507500_RKB, +0.211728763205541276296151308493989896E+0_RKB , +1.118297174119344981546693309349106980_RKB, +0.213475583035633628019879947303927958E+0_RKB , +1.110938046013575721417560779257849040_RKB, +0.215233842096659846410648766825208954E+0_RKB , +1.103541679424639718350709546845052450_RKB, +0.217003748300134423613077654918982009E+0_RKB , +1.096106627852021437094938365415991340_RKB, +0.218785517105043099072370007214575357E+0_RKB , +1.088631390653979821403993213445028160_RKB, +0.220579371908355906900178024260990122E+0_RKB , +1.081114409703403838077538136757234410_RKB, +0.222385544462441594762945169415386684E+0_RKB , +1.073554065792436288292686500464555760_RKB, +0.224204275321698924941276382479365999E+0_RKB , +1.065948674762122501754284026538321330_RKB, +0.226035814320961132564753113117134625E+0_RKB , +1.058296483330675084513966896229645790_RKB, +0.227880421088500051269826182271994471E+0_RKB , +1.050595664590929901514279329073961990_RKB, +0.229738365596760291802256320937473869E+0_RKB , +1.042844313144148970939980229020163640_RKB, +0.231609928754296215469589885980076311E+0_RKB , +1.035040439833440875887862746039381010_RKB, +0.233495403042770916853974440099008843E+0_RKB , +1.027181966035645772350639887939364020_RKB, +0.235395093203313594481836509609421923E+0_RKB , +1.019266717465484244962537467525869270_RKB, +0.237309316977027237519675921574483765E+0_RKB , +1.011292417439995739530489041191619980_RKB, +0.239238405905001516168070540916910782E+0_RKB , +1.003256679544672977063838476902952280_RKB, +0.241182706193826750302150947619295807E+0_RKB , +0.995156999635090923837912834290083799_RKB, +0.243142579653336370820347935962210089E+0_RKB , +0.986990747099062472368807733566367723_RKB, +0.245118404714142202924320107980890993E+0_RKB , +0.978755155294224603880824209605885949_RKB, +0.247110577533486783260721039414118216E+0_RKB , +0.970447311064224450680967868251783851_RKB, +0.249119513199040723215271175059742679E+0_RKB , +0.962064143223040583869351754884239000_RKB, +0.251145647041545878684196026994747375E+0_RKB , +0.953602409881086036147944393710646946_RKB, +0.253189436068676791163884011564958290E+0_RKB , +0.945058684468165463037907528952905452_RKB, +0.255251360534199633721355034811644515E+0_RKB , +0.936429340286575141234349646203595494_RKB, +0.257331925658493337610224432667231202E+0_RKB , +0.927710533402000123870677193352685174_RKB, +0.259431663518814566212074318832185428E+0_RKB , +0.918898183649590612180034442455129809_RKB, +0.261551135130401113878336401593219032E+0_RKB , +0.909987953496718494483529567690366580_RKB, +0.263690932742695838070411741690697980E+0_RKB , +0.900975224461221833746547856386022859_RKB, +0.265851682378732029260877257163356597E+0_RKB , +0.891855070732941566850586789359498648_RKB, +0.268034046650170417793435080776528378E+0_RKB , +0.882622229585165554772936671621819385_RKB, +0.270238727885765625479222906930855857E+0_RKB , +0.873271068088860754125762716220304264_RKB, +0.272466471617349972495381721975295691E+0_RKB , +0.863795545553308854813178505394360638_RKB, +0.274718070474985863152207934163143218E+0_RKB , +0.854189171008163807454180162989399104_RKB, +0.276994368552045124993231875042116081E+0_RKB , +0.844444954909153918889582440732428571_RKB, +0.279296266311992916126496729438627603E+0_RKB , +0.834555354086382178924726895193815695_RKB, +0.281624726122054644081592741705012005E+0_RKB , +0.824512208752292130518310689451625822_RKB, +0.283980778515329245279710753274268026E+0_RKB , +0.814306670135215230392694899997583155_RKB, +0.286365529303059635938328101021065686E+0_RKB , +0.803929116989971220407539518038181495_RKB, +0.288780167683694362995818015176624321E+0_RKB , +0.793369058840623296211094246674767659_RKB, +0.291225975526402318340687192537257840E+0_RKB , +0.782615023307233120893558043746138323_RKB, +0.293704338045591948359518681668325255E+0_RKB , +0.771654424224568084749572873233895398_RKB, +0.296216756132081268041022602880704688E+0_RKB , +0.760473406430108029348112105521972518_RKB, +0.298764860669019852359816171738518807E+0_RKB , +0.749056662017815292302576863549466866_RKB, +0.301350429240767224099410447613497339E+0_RKB , +0.737387211434295591278302895320305406_RKB, +0.303975405746574722328106158035369533E+0_RKB , +0.725446140909999639160421404681071701_RKB, +0.306641923566284096197801960631070354E+0_RKB , +0.713212285190975958395437234225351400_RKB, +0.309352333103853461802712328689370145E+0_RKB , +0.700661841106815072627797458756938969_RKB, +0.312109234772742761743862339129657007E+0_RKB , +0.687767892795788534294858623414951669_RKB, +0.314915518808718397997156048518493503E+0_RKB , +0.674499822837293822822291441953147501_RKB, +0.317774413735206587646816278462680542E+0_RKB , +0.660822574244419738417074112845703024_RKB, +0.320689545915737438541580666581786760E+0_RKB , +0.646695714894993817513389454402005337_RKB, +0.323665013485929872609853214812546138E+0_RKB , +0.632072236386061170945000136838048409_RKB, +0.326705479185682685503639905197287285E+0_RKB , +0.616896990007751449983468424580333684_RKB, +0.329816288403562001297942710464242773E+0_RKB , +0.601104617755992621533900682881952269_RKB, +0.333003621412417574590814956444079152E+0_RKB , +0.584616766106379321441587601292714165_RKB, +0.336274692838645610198728629890296241E+0_RKB , +0.567338257053818748196811566000406618_RKB, +0.339638017760732372141674530066184563E+0_RKB , +0.549151702327165120668100504067842453_RKB, +0.343103774061966311836681659618112095E+0_RKB , +0.529909720661558116786810165407173123_RKB, +0.346684307694080825876172229626686798E+0_RKB , +0.509423329602091814469823299066412422_RKB, +0.350394856987006815154163453112784578E+0_RKB , +0.487443966139236039301073245095571196_RKB, +0.354254625523424624005573055746854654E+0_RKB , +0.463634336790882217507922976793371502_RKB, +0.358288435101351989902170775658332694E+0_RKB , +0.437518402207871681933515025173607280_RKB, +0.362529398255472763687561092414814622E+0_RKB , +0.408389134611991145290558016416221589_RKB, +0.367023508970343116977068094647372845E+0_RKB , +0.375121332878380591495093443929722987_RKB, +0.371838172174307847618293715165674310E+0_RKB , +0.335737519214425235638195399148542308_RKB, +0.377079825919318504715611620323180171E+0_RKB , +0.286174591792072510002201653739714122_RKB, +0.382936353792390580381634933484297406E+0_RKB , +0.215241895984881699325976137068393403_RKB, +0.389807180887844207493515693365586429E+0_RKB , +0.000000000000000000000000000000000000_RKB, +0.398942280401432677939946059934381874E+0_RKB ], shape = [2, 128]) |
Definition at line 1618 of file pm_distNorm.F90.