pm_mathSum::getDot Interface Reference

Generate and return the expression dot_product(x, y) accurately (almost without roundoff error).
More...

Detailed Description

Generate and return the expression dot_product(x, y) accurately (almost without roundoff error).

Parameters

[in]	x	: The input contiguous vector of arbitrary size, of type complex of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128), or type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), representing the x value whose dot product with y is to be returned.
[in]	y	: The input contiguous vector of the same size, type, and kind as the input x, of representing the y values whose dot product with x is to be returned.
[in]	method	: The input scalar object that can be, the constant iteration or equivalently, an object of type iteration_type. Specifying this option forces the use of normal iterative approach to summing all array elements. This option is equivalent to the default implementations of the Fortran intrinsic sum(). This approach is the fastest serial method among all, but also generally the least accurate. the constant recursion or equivalently, an object of type recursion_type. Specifying this option forces the use of recursive pairwise approach to summing all array elements. the constant kahanbabu or equivalently, an object of type kahanbabu_type. Specifying this option forces the use of the Kahan-Babuska compensated approach to summing all array elements. This algorithm, while accurate, can be up to 2-4 times more expensive than the iterative approach discussed above. the constant fablocked or equivalently, an object of type fablocked_type. Specifying this option forces the use of the Fast Accurate Blocked approach to summing all array elements. the constant nablocked or equivalently, an object of type nablocked_type. Specifying this option forces the use of the Naive Blocked approach to summing all array elements. The presence of this argument is merely for compile-time resolution of the procedures of this generic interface. (optional, default = fablocked.)

Returns

dotres : The output scalar of the same type and kind containing the result of the dot product of the input x and y vectors.

Possible calling interfaces ⛓

use pm_mathSum, only: getDot, iteration, recursion, kahanbabu, fablocked, nablocked
 
dotres = getDot(x, y)
dotres = getDot(x, y, method)

Warning

The returned value is 0 is the size of the condition size(x) == 0 holds.
The condition size(x) == size(y) must hold for the corresponding input arguments.
This condition is verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

See also

get1mexp
getLog1p
getCumSum
getLogAddExp
getLogSubExp
getLogSumExp

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK, LK, RKH
    use pm_distUnif, only: setUnifRand
    use pm_arrayRank, only: getRankDense
    use pm_arraySpace, only: setLinSpace
    use pm_mathSum, only: getDot, iteration, recursion, kahanbabu, fablocked, nablocked
    use pm_io, only: display_type
 
    implicit none
 
    real(RKH) :: truth
    real(RKH), allocatable :: dotres(:), relerr(:)
    type(display_type) :: disp
 
    disp = display_type(file = "main.out.F90")
 
    block
        use pm_kind, only: TKG => RKS
        integer(IK), parameter :: lenx = 10**7
        real(TKG) :: x(lenx), y(lenx), lb, ub
        call disp%skip()
        call disp%show("lenx")
        call disp%show( lenx )
        call disp%show("lb = real(lenx, TKG); ub = 1._TKG")
                        lb = real(lenx, TKG); ub = 1._TKG
        call disp%show("call setLinSpace(x, lb, ub) ! call setUnifRand(x)")
                        call setLinSpace(x, lb, ub) ! call setUnifRand(x)
        call disp%show("y = 1 !/ x")
                        y = 1 !/ x
        call disp%show("truth = (real(ub, TKG) + real(lb, RKH)) * size(x, 1, IK) / 2 ! reference high-precision value for comparison")
                        truth = (real(ub, TKG) + real(lb, RKH)) * size(x, 1, IK) / 2 ! reference high-precision value for comparison
        call disp%show("truth")
        call disp%show( truth )
        call disp%show("dotres = [getDot(x, y), getDot(x, y, iteration), getDot(x, y, recursion), getDot(x, y, kahanbabu), getDot(x, y, fablocked), getDot(x, y, nablocked)]")
                        dotres = [getDot(x, y), getDot(x, y, iteration), getDot(x, y, recursion), getDot(x, y, kahanbabu), getDot(x, y, fablocked), getDot(x, y, nablocked)]
        call disp%show("dotres")
        call disp%show( dotres )
        call disp%show("relerr = abs(truth - dotres) / truth")
                        relerr = abs(truth - dotres) / truth
        call disp%show("relerr")
        call disp%show( relerr )
        call disp%show("getRankDense(relerr)")
        call disp%show( getRankDense(relerr) )
        call disp%skip()
    end block
 
    block
        use pm_kind, only: TKG => RKD
        integer(IK), parameter :: lenx = 10**8
        real(TKG) :: x(lenx), y(lenx), lb, ub
        call disp%skip()
        call disp%show("lenx")
        call disp%show( lenx )
        call disp%show("lb = real(lenx, TKG); ub = 1._TKG")
                        lb = real(lenx, TKG); ub = 1._TKG
        call disp%show("call setLinSpace(x, lb, ub) ! call setUnifRand(x)")
                        call setLinSpace(x, lb, ub) ! call setUnifRand(x)
        call disp%show("y = 1 !/ x")
                        y = 1 !/ x
        call disp%show("truth = (real(ub, TKG) + real(lb, RKH)) * size(x, 1, IK) / 2 ! reference high-precision value for comparison")
                        truth = (real(ub, TKG) + real(lb, RKH)) * size(x, 1, IK) / 2 ! reference high-precision value for comparison
        call disp%show("truth")
        call disp%show( truth )
        call disp%show("dotres = [getDot(x, y), getDot(x, y, iteration), getDot(x, y, recursion), getDot(x, y, kahanbabu), getDot(x, y, fablocked), getDot(x, y, nablocked)]")
                        dotres = [getDot(x, y), getDot(x, y, iteration), getDot(x, y, recursion), getDot(x, y, kahanbabu), getDot(x, y, fablocked), getDot(x, y, nablocked)]
        call disp%show("dotres")
        call disp%show( dotres )
        call disp%show("relerr = abs(truth - dotres) / truth")
                        relerr = abs(truth - dotres) / truth
        call disp%show("relerr")
        call disp%show( relerr )
        call disp%show("getRankDense(relerr)")
        call disp%show( getRankDense(relerr) )
        call disp%skip()
    end block
 
    block
        call disp%skip()
        call disp%show("[getDot([real ::], [real ::]), getDot([real :: 1], [real :: 1]), getDot([real :: 1, 1], [real :: 1, 1]), getDot([real :: 1, 1, 1], [real :: 1, 1, 1])]")
        call disp%show( [getDot([real ::], [real ::]), getDot([real :: 1], [real :: 1]), getDot([real :: 1, 1], [real :: 1, 1]), getDot([real :: 1, 1, 1], [real :: 1, 1, 1])] )
        call disp%skip()
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
lenx
+10000000
lb = real(lenx, TKG); ub = 1._TKG
call setLinSpace(x, lb, ub) ! call setUnifRand(x)
y = 1 !/ x
truth = (real(ub, TKG) + real(lb, RKH)) * size(x, 1, IK) / 2 ! reference high-precision value for comparison
truth
+50000005000000.0000000000000000000000
dotres = [getDot(x, y), getDot(x, y, iteration), getDot(x, y, recursion), getDot(x, y, kahanbabu), getDot(x, y, fablocked), getDot(x, y, nablocked)]
dotres
+50000000188416.0000000000000000000000, +49423623127040.0000000000000000000000, +50000008577024.0000000000000000000000, +50000004382720.0000000000000000000000, +50000000188416.0000000000000000000000, +49999983411200.0000000000000000000000
relerr = abs(truth - dotres) / truth
relerr
+0.962316703768329623167037683296231645E-7, +0.115276363064363693563630643636935635E-1, +0.715404728459527154047284595271540462E-7, +0.123455987654401234559876544012345606E-7, +0.962316703768329623167037683296231645E-7, +0.431775956822404317759568224043177598E-6
getRankDense(relerr)
+3, +5, +2, +1, +3, +4
 
 
lenx
+100000000
lb = real(lenx, TKG); ub = 1._TKG
call setLinSpace(x, lb, ub) ! call setUnifRand(x)
y = 1 !/ x
truth = (real(ub, TKG) + real(lb, RKH)) * size(x, 1, IK) / 2 ! reference high-precision value for comparison
truth
+5000000050000000.00000000000000000000
dotres = [getDot(x, y), getDot(x, y, iteration), getDot(x, y, recursion), getDot(x, y, kahanbabu), getDot(x, y, fablocked), getDot(x, y, nablocked)]
dotres
+5000000050000000.00000000000000000000, +5000000050000000.00000000000000000000, +5000000050000000.00000000000000000000, +5000000050000000.00000000000000000000, +5000000050000000.00000000000000000000, +5000000050000000.00000000000000000000
relerr = abs(truth - dotres) / truth
relerr
+0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
getRankDense(relerr)
+1, +1, +1, +1, +1, +1
 
 
[getDot([real ::], [real ::]), getDot([real :: 1], [real :: 1]), getDot([real :: 1, 1], [real :: 1, 1]), getDot([real :: 1, 1, 1], [real :: 1, 1, 1])]
+0.00000000, +1.00000000, +2.00000000, +3.00000000
 
 

Benchmarks:

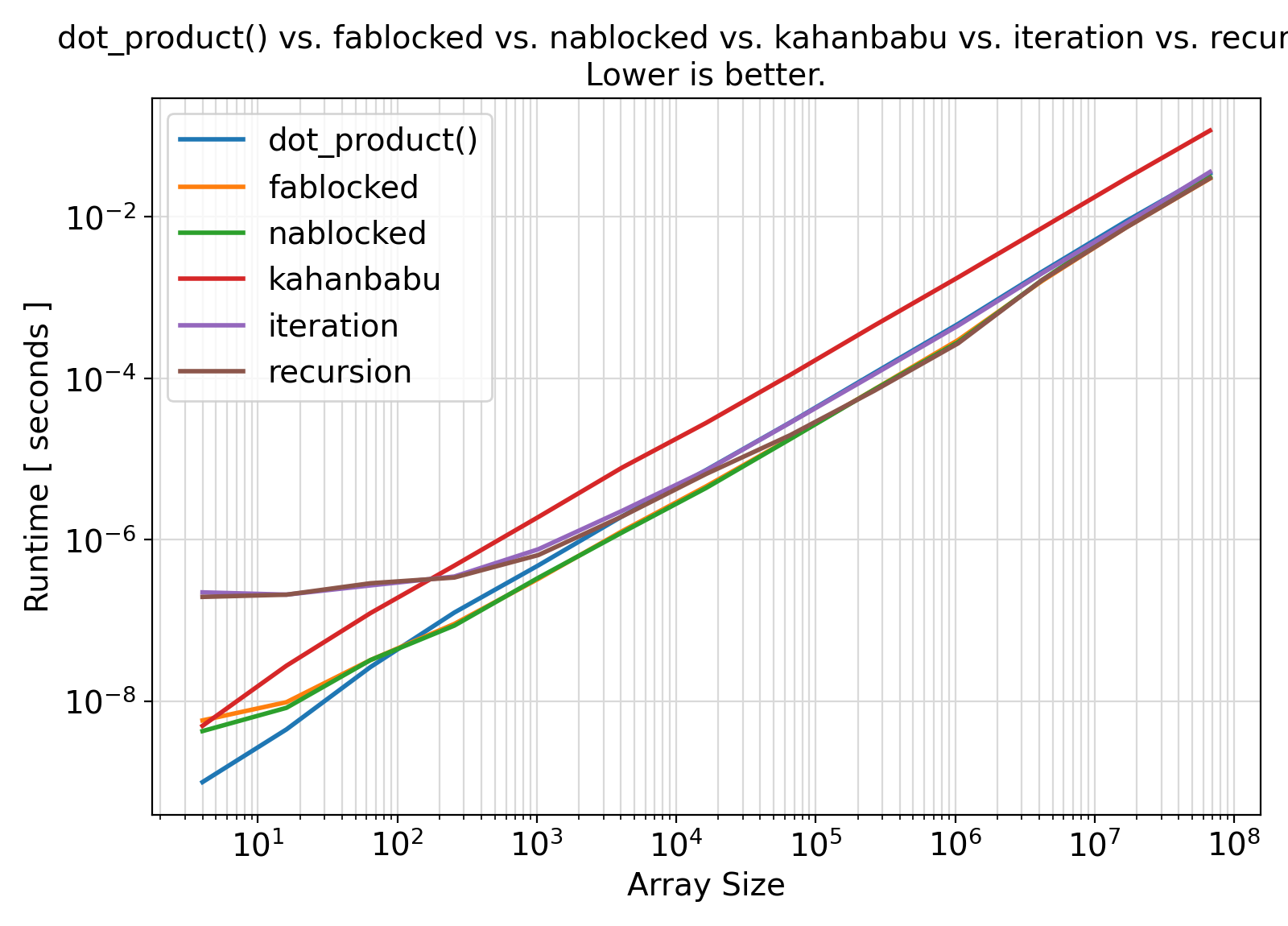
Benchmark :: The effects of method on runtime efficiency ⛓

The following program compares the runtime performance of getDot algorithms with the default Fortran dot_product() intrinsic function.

! Test the performance of `getDot()` with and without the selection `control` argument.
program benchmark
 
    use pm_bench, only: bench_type
    use pm_distUnif, only: setUnifRand
    use pm_mathCumSum, only: setCumSum
    use pm_arrayResize, only: setResized
    use pm_kind, only: SK, IK, LK, RKH, RK, RKG => RKD
    use iso_fortran_env, only: error_unit
 
    implicit none
 
    integer(IK)                         :: ibench
    integer(IK)                         :: iarr
    integer(IK)                         :: arrlen
    integer(IK)                         :: fileUnit
    real(RKG)                           :: dumsum = 0._RKG
    real(RKG)                           :: array(10**8)
    real(RKG)                           :: dotres
    type(bench_type)    , allocatable   :: bench(:)
    logical(LK)                         :: underflowEnabled
 
    bench = [ bench_type(name = SK_"dot_product()", exec = getDotFortran, overhead = setOverhead) &
            , bench_type(name = SK_"fablocked", exec = getDotFAB, overhead = setOverhead) &
            , bench_type(name = SK_"nablocked", exec = getDotNAB, overhead = setOverhead) &
            , bench_type(name = SK_"kahanbabu", exec = getDotKAB, overhead = setOverhead) &
            , bench_type(name = SK_"iteration", exec = getDotIte, overhead = setOverhead) &
            , bench_type(name = SK_"recursion", exec = getDotRec, overhead = setOverhead) &
            ]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "dot_product() vs. getDot()"
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        call setUnifRand(array)
        !truth = array; call setCumSum(truth)
        write(fileUnit, "(*(g0,:,','))") "Array Size", (bench(ibench)%name, ibench = 1, size(bench))
        loopOverArraySize: do iarr = 2, 26, 2
 
            arrlen = 2**iarr
            write(*,"(*(g0,:,' '))") "Benchmarking with array size", arrlen
            do ibench = 1, size(bench)
                bench(ibench)%timing = bench(ibench)%getTiming(minsec = 0.07_RK)
            end do
            write(fileUnit,"(*(g0,:,','))") arrlen, (bench(ibench)%timing%mean, ibench = 1, size(bench))
 
        end do loopOverArraySize
        write(*,"(*(g0,:,' '))") dumsum
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call getDummy()
    end subroutine
 
    subroutine getDummy()
        dumsum = dumsum + dotres
    end subroutine
 
    subroutine getDotFortran()
        dotres = dot_product(array(1 : arrlen), array(1 : arrlen))
        call getDummy()
    end subroutine
 
    subroutine getDotFAB()
        use pm_mathSum, only: getDot!, fablocked
        dotres = getDot(array(1 : arrlen), array(1 : arrlen))!, fablocked)
        call getDummy()
    end subroutine
 
    subroutine getDotNAB()
        use pm_mathSum, only: getDot, nablocked
        dotres = getDot(array(1 : arrlen), array(1 : arrlen), nablocked)
        call getDummy()
    end subroutine
 
    subroutine getDotKAB()
        use pm_mathSum, only: getDot, kahanbabu
        dotres = getDot(array(1 : arrlen), array(1 : arrlen), kahanbabu)
        call getDummy()
    end subroutine
 
    subroutine getDotIte()
        use pm_mathSum, only: getDot, iteration
        dotres = getDot(array(1 : arrlen), array(1 : arrlen), iteration)
        call getDummy()
    end subroutine
 
    subroutine getDotRec()
        use pm_mathSum, only: getDot, recursion
        dotres = getDot(array(1 : arrlen), array(1 : arrlen), recursion)
        call getDummy()
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ",")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
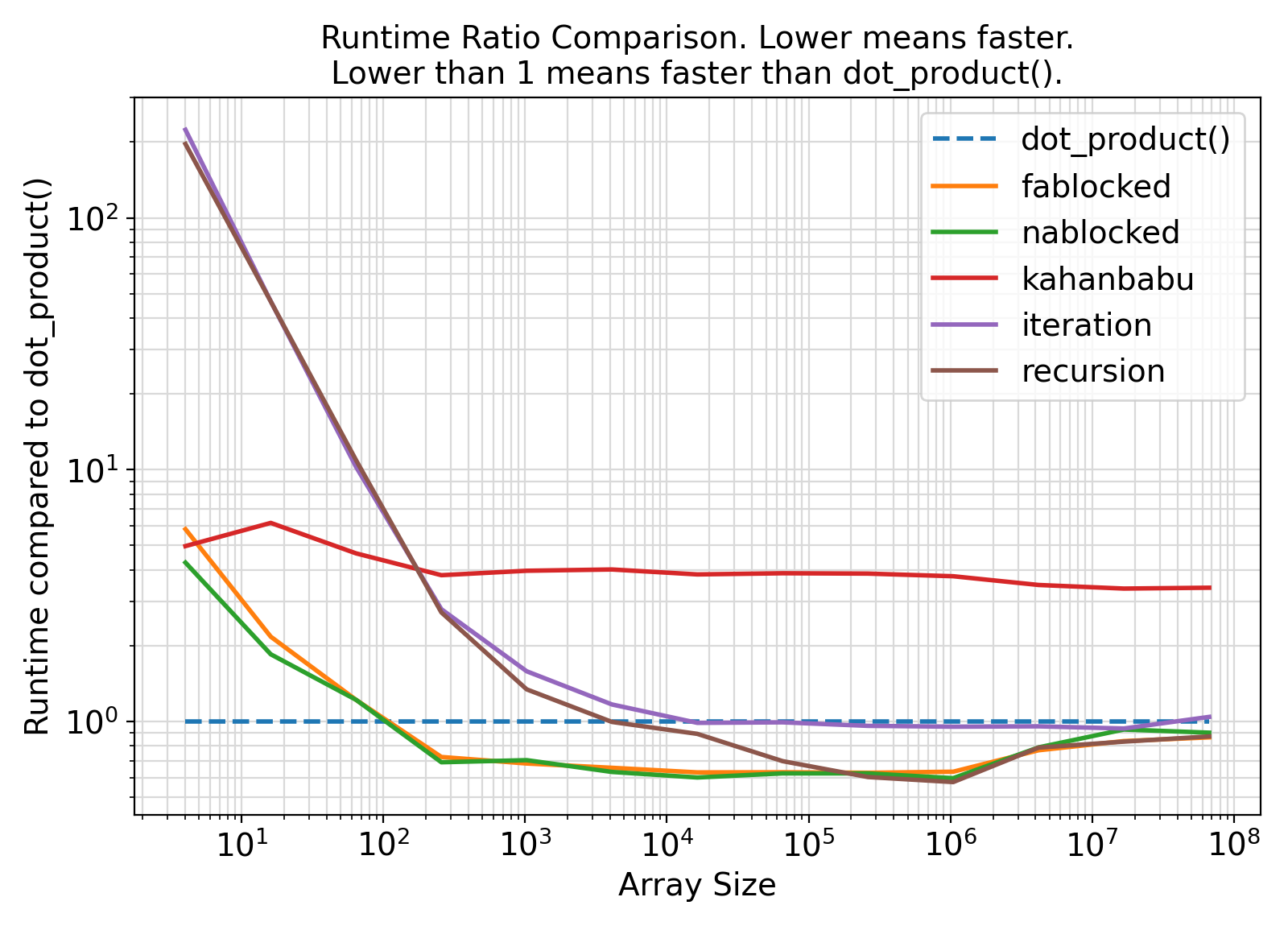
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}.".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

1. Among all summation algorithms, fablocked_type appears to offer the most accurate result while also being even faster than the default Fortran dot_product() and all other implemented summation algorithms for array sizes > 100.
   

Test:

test_pm_mathSum

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, August 8, 2024, 10:23 PM, NASA Goddard Space Flight Center, Washington, D.C.

Definition at line 1247 of file pm_mathSum.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_mathSum.F90