Programming glossary
The following table contains some technical programming phrases that are often used and heard in the field of computer science and programming, that you need to be familiar as well.
| Expression | Description |
|---|---|
| algorithm | A general method for solving a class of problems. |
| bug | An error in program that has to be resolved for successful execution of the program. |
| compiled language | A programming language whose programs need to be compiled by a compiler in order to run. |
| compiler | A software that translates an entire high-level program into a lower-level language to make it executable. |
| debugging | The process of finding and removing any type of error in the program. |
| exception | An alternative name for runtime error in the program. |
| executable | An object code, ready to be executed. Generally has the file extension .exe or .out or no extension at all. |
| formal language | A language that is intentionally designed for specific purposes, which, unlike natural languages, follows a strict standard. |
| high-level language | A programming language (e.g., Python, Fortran, Java, etc) that has high level of abstraction from the underlying hardware. |
| interpreted language | A programming language whose statements are interpreted line-by-line by an interpreter and immediately executed. |
| low-level language | A programming language that has a low-level of abstraction from computer hardware and architecture, such as Assembly. Very close to machine code. |
| natural language | A language that evolves naturally, and has looser syntax rules and standard compared to formal languages. |
| object code | The output of a compiler after translating a program. |
| parsing | Reading and examining a file/program and analyzing the syntactic structure of the file/program. |
| portability | A program's ability to be exucatable on more than one kind of computer architecture, without changing the code. |
| problem solving | The process of formulating a problem and finding and expressing a solution to it. |
| program | A set of instructions in a that together specify an algorithm a computation. |
| runtime error | An error that does not arise and cause the program to stop, until the program has started to execute. |
| script | A program in an interpreted language stored in a file. |
| semantic error | A type of error in a program that makes the program do something other than what was intended. Catching these errors can be very tricky. |
| semantics | The meaning of a program. |
| source code | A program in a high-level compiled language, before being compiled by the compiler. |
| syntax error | A type of error in program that violates the standard syntax of the programming language, and hence, the program cannot be interpreted or compiled until the syntax error is resolved. |
| syntax | The structure of a program. |
| token | One of the basic elements of the syntactic structure of a program, in analogy with word in a natural language. |
| dictionary | A collection of `key:value` mapping pairs, in which the values can be obtained by calling the value's key. |
| hashable | A Python object (e.g., variable) that has a hash value which never changes during its lifetime. |
| immutable | A variable or value that cannot be modified. Assignments to elements of immutable values cause a runtime error. Example immutable Python entities are tuples and strings. |
| invocation | The process of calling an object's method, usually done through <object name>.<method name> notation. |
| list | A sequence of comma-separated heterogenous values next to each other. |
| method | Similar to a function, a method is a predefined built-in Python script that performs a specific task on the data object to which the method belongs. |
| mutable | A variable or value that can be modified. Examples of mutables in Python are lists, and dictionaries. |
| set | An unordered collection of unique elements, just like the mathemtical sets. |
| string | A sequence of characters next to each other. |
| tuple | An immutable data value that contains related elements. Tuples are used to group together related data, such as a person’s name, their age, and their gender. |
The binary representation of data and instructions
In the early days of computing, around 1950’, there was no consensus on how data, in particular numbers, should be represented in the computer hardware. But as time went by, the entire community has converged to representing all data and numerics in binary in computers. The advantage and simplicity of using binary 0 and 1 to represent data may be obvious; 0 and 1 are easy to represent electronically. For example, the flow of the lack of flow of electric current could be used to represent 0 and 1. Alternatively, the presence or lack of a charge or magnetism in a particular location in the memory could be used to represent 0 and 1. Therefore, anything represented as a binary number can also be stored in computer memory and processed.
The tiniest unit of information in computer and information science is a bit. A bit of information can either represent 0 or 1. Of particular significance is the binary representation of real numbers. Modern computer architectures use multiple different bit chunks (frequently 32, 64, and 128 bits) of information to store real numbers. The following figures represent the most common storage patterns of real numbers in modern computers.
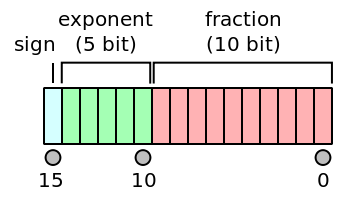

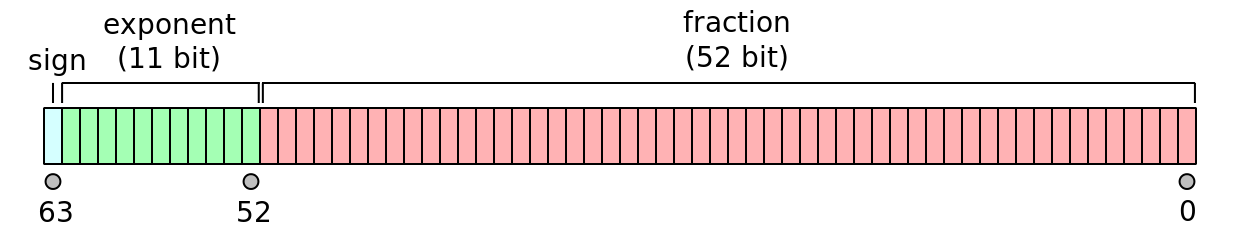

As seen, each real number is represented by its significant digits (23-bits) and its exponent (8-bits), and its sign (which is represented by only one bit of information). It is obvious from this illustration that not all real numbers could be represented by 23 bits for significant digits.
One could use more than 64 bits to represent real numbers more precisely. However, the higher the number of bits, the more demanding the computations and the storage of the numbers will become. As such, most modern computers and computer programming languages only enable the default real number representation by 64 bits. Some (like Fortran, C, C++, and Python) also provide 128-bit real number representation for very large or highly accurate real number representations.
The following real-32 bits examples illustrate how real numbers are stored in such chunks of bits in computers. These examples are given in bit representation, in hexadecimal and binary, of the floating-point value. This includes the sign, exponent, and significand.
0 00000000 00000000000000000000001 = 0000 0001 = 2^−126 × 2^−23 = 2^−149 ≈ 1.4012984643 × 10^-45
(smallest positive subnormal number)
0 00000000 11111111111111111111111 = 007f ffff = 2^-126 × (1 - 2^-23) ≈ 1.1754942107 ×10^-38
(largest subnormal number)
0 00000001 00000000000000000000000 = 0080 0000 = 2^-126 ≈ 1.1754943508 × 10^-38
(smallest positive normal number)
0 11111110 11111111111111111111111 = 7f7f ffff = 2127 × (2 − 2^-23) ≈ 3.4028234664 × 1038
(largest normal number)
0 01111110 11111111111111111111111 = 3f7f ffff = 1 − 2^-24 ≈ 0.999999940395355225
(largest number less than one)
0 01111111 00000000000000000000000 = 3f80 0000 = 1 (one)
0 01111111 00000000000000000000001 = 3f80 0001 = 1 + 2^-23 ≈ 1.00000011920928955
(smallest number larger than one)
1 10000000 00000000000000000000000 = c000 0000 = −2
0 00000000 00000000000000000000000 = 0000 0000 = 0
1 00000000 00000000000000000000000 = 8000 0000 = −0
0 11111111 00000000000000000000000 = 7f80 0000 = infinity
1 11111111 00000000000000000000000 = ff80 0000 = −infinity
0 10000000 10010010000111111011011 = 4049 0fdb ≈ 3.14159274101257324 ≈ π ( pi )
0 01111101 01010101010101010101011 = 3eaa aaab ≈ 0.333333343267440796 ≈ 1/3
In the above examples, all left-hand-side numbers are binary, all middle numbers are hexadecimal representations of the same binary numbers, and all right-hand-side numbers are the corresponding decimal equivalents.
Note that by convention, the digit 1 is always implicitly present behind the fractional component of real number representations. Therefore, it makes sense for the decimal number 1 to have all its significands (the mantissa or the fractional component) to be zeros 00000000000000000000000.
One can immediately conclude that there are 223×126=1,056,964,608 unique real numbers that can be represented with IEEE 32-bit real number format.
A problem immediately arises with the representation of real numbers in computers. A N-bits amount of information (where X is an arbitrary integer) can represent only a limited set of real numbers. There are, however, an uncountably infinite number of real numbers.

It is easy math to show that the interval [0,1) already contains a quarter of all representable IEEE 32-bit real numbers by all computers. In other words, half of IEEE 32-bit real numbers are in the range [−1,−1].
The contents of a computer program
Although different programming languages look different in their syntax standards, virtually all programming languages are comprised of the following major components (instructions):
- input
Virtually every program starts with some input data by the user or the input data that is hard-coded in the program.
- mathematical/logical operations
Virtually all programs involve mathematical or logical operations on the input data to the program.
- conditional execution
To perform the above operations on data, most often (but not always) there is a need to check if some conditions are met in the program and then perform specific programming instructions corresponding to each.
- repetition / looping
It is frequently needed to perform a specific set of operations repeatedly in the program to achieve its goal.
- output
At the end of the program, it is always needed to output the program result, either to a computer screen or to a file.
Debugging a program
As it is obvious from its name, a bug in a computer program is an annoying programming error that needs fixing for the program to become executable or to give out the correct answer. The process of removing program bugs is called debugging. There are three types of programming bugs (errors):
Syntax error
A program can be successfully run only if it is syntactically correct, whether interpreted or compiled. Syntax errors are related to the structure and standard of the language and the order by which the language tokens are allowed to appear in the code. For example, the following Python print statement is a syntax error in Python 3 standard, whereas it was considered to be the correct syntax for print in Python 2 standard.
print 'Hello World!'
File "<ipython-input-21-10fdc521e430>", line 1
print 'Hello World!'
^
SyntaxError: Missing parentheses in call to 'print'
The syntactically-correct usage of print in Python 3 would be,
print ('Hello World!')
Hello World!
Runtime error
Runtime errors or sometimes also named exceptions are a class of programming errors that can be detected only at the time of running the code; that is, they are not syntax errors. Examples include:
- memory leaks (prevalent error in beginner C and C++ codes)
- uninitialized memory
- access request to an illegal memory address of the computer
- security attack vulnerabilities
- buffer overflow
These errors can sometimes be tricky to identify.
Semantic error
Unlike syntax errors that comprise something the compiler/interpreter does not understand, semantic errors do not cause any compiler/interpreter error messages. However, the resulting compiled/interpreted code will NOT do what it is intended to do. Semantic errors are the most dangerous types of programming errors, as they do not raise any error flag by the compiler/interpreter, yet the program will not do what it is intended to do, although the code may look perfectly fine on its face. A semantic error is almost synonymous with logical error. Dividing two integers using the regular division operator / in Python 2 and expecting the result to be real would result in a semantic error. This is because, in Python 2 standard, the regular division operator is equivalent to integer division for integer operands:
In Python 2,
2/7
0
Whereas, you might have meant a float division by using /, as in Python 3,
2/7
0.2857142857142857