pm_matrixInv Module Reference

This module contains abstract and concrete derived types and procedures related to the inversion of square matrices.
More...

Data Types
interface	getMatInv
	Generate and return the full inverse of an input matrix of general or triangular form directly or through its input the LU/Cholesky factorization. More...
type	inversion_type
	This is a concrete derived type whose instances are exclusively used to request inversion operation on a given matrix within an interface of a procedure of the ParaMonte library. More...
interface	setMatInv
	Generate and return the full inverse of a general or triangular matrix or a subset of the inverse of a positive-definite matrix complementary to its specified Cholesky factorization subset. More...

Variables
character(*, SK), parameter	MODULE_NAME = "@pm_matrixInv"
type(inversion_type), parameter	inversion = inversion_type()
	This is a scalar parameter object of type inversion_type that is exclusively used to request no transpose of a given matrix within an interface of a procedure of the ParaMonte library. More...

Detailed Description

This module contains abstract and concrete derived types and procedures related to the inversion of square matrices.

Inversion operation

In linear algebra, an \(n\)-by- \(n\) square matrix \(A\) is called invertible (also nonsingular, nondegenerate), if there exists an \(n\)-by- \(n\) square matrix \(B\) such that,

\begin{equation} \mathbf{AB} = \mathbf{BA} = \mathbf{I}_{n}~, \end{equation}

where \(I_n\) denotes the \(n\)-by- \(n\) identity matrix and the multiplication used is ordinary matrix multiplication.
If this is the case, then the matrix \(B\) is uniquely determined by \(A\), and is called the **(multiplicative) inverse** of \(A\), denoted by \(A^{−1}\).
source inversion is the process of finding the matrix \(B\) that satisfies the prior equation for a given invertible matrix \(A\).
Over a field, a square matrix that is not invertible is called singular or degenerate.
A square matrix with entries in a field is singular if and only if its determinant is zero.
Singular matrices are rare in the sense that if a square matrix entries are randomly selected from any bounded region on the number line or complex plane, the probability that the matrix is singular is \(0\), that is, it will almost never be singular.
Non-square matrices do not have an inverse.
However, in some cases such a matrix may have a left inverse or right inverse.
If \(A\) is \(m\)-by- \(n\) and the rank of \(A\) is equal to \(n\) ( \(n \leq m\)), then \(A\) has a left inverse, an \(n\)-by- \(m\) matrix \(B\) such that \(BA = I_n\).
If \(A\) has rank \(m\) ( \(m \leq n\)), then it has a right inverse, an \(n\)-by- \(m\) matrix \(B\) such that \(AB = I_m\).

Inverse matrix properties

The following properties hold for an invertible matrix \(A\):

1. \((\mathbf{A}^{-1})^{-1} = \mathbf{A}\).
   
2. \((k\mathbf{A})^{-1} = k^{-1}\mathbf{A}^{-1}\) for nonzero scalar \(k\).
   
3. \((\mathbf{Ax})^{+} = \mathbf{x}^{+}\mathbf{A}^{-1}\) if \(A\) has orthonormal columns, where \(+\) denotes the Moore–Penrose inverse and \(x\) is a vector.
   
4. \((\mathbf{A}^{\mathrm{T}})^{-1} = (\mathbf{A}^{-1})^{\mathrm{T}}\).
   
5. For any invertible \(n\)-by- \(n\) matrices \(A\) and \(B\), \((\mathbf{AB})^{-1} = \mathbf{B}^{-1}\mathbf{A}^{-1}\).
   More generally, if \(\mathbf{A}_1, \dots, \mathbf{A}_{k}\) are invertible \(n\)-by- \(n\) matrices, then \((\mathbf{A}_{1}\mathbf{A}_{2} \cdots \mathbf{A}_{k-1}\mathbf{A}_{k})^{-1} = \mathbf{A}_{k}^{-1}\mathbf{A}_{k-1}^{-1} \cdots \mathbf{A}_{2}^{-1}\mathbf{A}_{1}^{-1}\).
   
6. \(\det\mathbf{A}^{-1} = (\det \mathbf{A})^{-1}\).
   
7. The rows of the inverse matrix \(V\) of a matrix \(U\) are orthonormal to the columns of \(U\).
   

Inverse matrix computation

The common approach to computing the inverse matrix stems from its definition.
The inverse matrix \(A^{-1}\) of a square matrix \(A\) is a square matrix such that \(AA^{-1} = I\), where \(I\) is the identity matrix.
Depending on the class of the square matrix \(A\), there are several approaches that can be taken to compute its inverse.
However, all such methods attempt to factorize the matrix first (for example, Cholesky decomposition or LU decomposition) and cast the problem into seeking the solution to a system of linear equations.
For example, for a general square matrix of shape \(3\times 3\), the corresponding system of equations to solve would be:

\begin{equation} \begin{bmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{bmatrix} \begin{bmatrix} A_{11}^{-1} & A_{12}^{-1} & A_{13}^{-1} \\ A_{21}^{-1} & A_{22}^{-1} & A_{23}^{-1} \\ A_{31}^{-1} & A_{32}^{-1} & A_{33}^{-1} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} ~, \end{equation}

where the second matrix on the left hand side is the inverse of the first square matrix \(A\).
The inverse matrix can be constructed as the collection of solutions to \(n = 3\) systems of equations of the form \(Ax=b\) with different right hand sides \(b\) matrices and \(x\) representing \(n^{\mathrm{th}}\) column of the inverse matrix.
The first system of equations to solve for the above problem would be:

\begin{equation} \begin{bmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{bmatrix} \begin{bmatrix} A_{11}^{-1} \\ A_{21}^{-1} \\ A_{31}^{-1} \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} ~. \end{equation}

The second column of the inverse can be computed by changing \(b\) to \([0,1,0]^T\), the third column with \([0,0,1]^T\), and so on.
The task of computing the inverse of the matrix is now reduced to solving a series of systems of linear equations.
This can be done if the matrix \(A\) is factorized into lower and upper triangular matrices,

\begin{equation} \begin{bmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{bmatrix} = \begin{bmatrix} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} ~, \end{bmatrix} \end{equation}

such that the above system can be written as,

\begin{equation} \begin{bmatrix} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33} \end{bmatrix} \left( \begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \end{bmatrix} \begin{bmatrix} A_{11}^{-1} \\ A_{21}^{-1} \\ A_{31}^{-1} \end{bmatrix} \right) = \begin{bmatrix} 1 \\ 0 \\ 0 ~. \end{bmatrix} \end{equation}

The above form of equations implied that the two systems of triangular equations have to be solved to obtain one column of the inverse matrix.
However, this method is fast because only back- and forward-substitution are required to solve for the column vectors after the initial factorization of the matrix \(A\).
The most common factorization methods used for \(A\) to obtain its inverse are:

1. Pivoted LU factorization for general square matrices.
   
2. Cholesky factorization for Symmetric/Hermitian Positive-Definite square matrices.
   

Inversion-Transposition operation

There are also special matrix operations that mix inversion with Symmetric and Hermitian each having corresponding matrix classes:**

1. Orthogonal transposition
   A square matrix whose transpose is equal to its inverse is called an Orthogonal matrix.
   In other words, \(A\) is Orthogonal if \(\mathbf{A}^{\up{T}} = \mathbf{A}^{-1}\).
   The corresponding transposition is called Orthogonal denoted by the operator \(\cdot^{\up{-T}}\).
   
2. Unitary transposition
   A square complex matrix whose transpose is equal to its conjugate inverse is called a Unitary matrix.
   In other words, \(A\) is Unitary if \(\mathbf{A}^{\up{T}} = {\overline{\mathbf{A}^{-1}}}\).
   The corresponding transposition is called Unitary denoted by the operator \(\cdot^{\up{-H}}\).
   

See also

pm_matrixDet
pm_matrixLUP
pm_matrixChol
pm_matrixTrans

Benchmarks:

Benchmark :: The runtime performance of setMatInv for various methods and inverse matrix subsets. ⛓

! Test the performance of Cholesky factorization computation using an assumed-shape interface vs. explicit-shape interface.
program benchmark
 
    use pm_kind, only: IK, LK, RKG => RKD, SK
    use pm_matrixCopy, only: setMatCopy, rdpack, uppDia, lowDia, transHerm
    use pm_distUnif, only: rngx_type => xoshiro256ssw_type
    use pm_arrayResize, only: setResized
    use pm_distUnif, only: getUnifRand
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: itry, ntry
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK)     , parameter         :: NARR = 10_IK
    integer(IK)     , allocatable       :: rperm(:)
    real(RKG)       , allocatable       :: mat(:,:), inv(:,:)
    type(bench_type), allocatable       :: bench(:)
    integer(IK)     , parameter         :: nsim = 2**NARR
    integer(IK)                         :: rank
    real(RKG)                           :: dumm
    type(rngx_type)                     :: rngx
 
    rngx = rngx_type()
    bench = [ bench_type(name = SK_"setMatInvLow", exec = setMatInvLow, overhead = setOverhead) &
            , bench_type(name = SK_"setMatInvUpp", exec = setMatInvUpp, overhead = setOverhead) &
            , bench_type(name = SK_"setMatInvLUP", exec = setMatInvLUP, overhead = setOverhead) &
#if         LAPACK_ENABLED
            , bench_type(name = SK_"lapack_dpotri", exec = lapack_dpotri, overhead = setOverhead) &
#endif
            ]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "inverse matrix benchmarking..."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "rank", (bench(i)%name, i = 1, size(bench))
 
        dumm = 0._RKG
        loopOverMatrixSize: do iarr = 1, NARR
 
            rank = 2**iarr
            ntry = nsim / rank
            call setResized(rperm, rank)
            call setResized(inv, [rank, rank])
            mat = getUnifRand(1._RKG, 2._RKG, rank, rank + 1_IK)
            write(*,"(*(g0,:,' '))") "Benchmarking setMatInv() algorithms with array size", rank, ntry
 
            do i = 1, size(bench)
                bench(i)%timing = bench(i)%getTiming()
            end do
 
            write(fileUnit,"(*(g0,:,','))") rank, (bench(i)%timing%mean / ntry, i = 1, size(bench))
 
        end do loopOverMatrixSize
        write(*,"(*(g0,:,' '))") dumm
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        do itry = 1, ntry
            call setMatrix()
        end do
    end subroutine
 
    subroutine setMatrix()
        !integer(IK) :: i
        !call random_number(mat)
        !mat = mat * 1.e-4_RKG
        !do i = 1, size(mat, dim = 1, kind = IK)
        !    mat(i,i+1) = 1._RKG
        !end do
        !use pm_distCov, only: setCovRand
        !call setCovRand(rngx, mat(:,2:rank+1)) ! causes numeric overflow for large matrix ranks.
        use pm_matrixInit, only: setMatInit, uppLowDia
        call setMatInit(mat(:,2:rank+1), uppLowDia, 0._RKG, 0._RKG, 1._RKG)
        dumm = dumm - mat(rank, rank) - mat(rank-1, rank-1)
    end subroutine
 
#if LAPACK_ENABLED
    subroutine lapack_dpotri()
        integer(IK) :: info
        do itry = 1, ntry
            call setMatrix()
            call dpotrf("U", rank, mat(:,2:rank+1), rank, info)
            if (info /= 0_IK) error stop
            call dpotri("U", rank, mat(:,2:rank+1), rank, info)
            if (info /= 0_IK) error stop
            call setMatCopy(mat(:,2:rank+1), rdpack, mat(:,1:rank), rdpack, uppDia, transHerm) ! symmetrize inverse matrix.
            !dumm = dumm + mat(rank,rank) + mat(rank-1,rank-1)
        end do
    end subroutine
#endif
 
    subroutine setMatInvLow()
        use pm_matrixInv, only: setMatInv, choUpp
        use pm_matrixChol, only: setMatChol, nothing
        integer(IK) :: info
        do itry = 1, ntry
            call setMatrix()
            call setMatChol(mat(:,2:rank+1), uppDia, info, mat(:,2:rank+1), nothing)
            if (info /= 0_IK) error stop
            call setMatInv(mat(:,1:rank), mat(:,2:rank+1), choUpp)
            !dumm = dumm + mat(rank,rank) + mat(rank-1,rank-1)
        end do
    end subroutine
 
    subroutine setMatInvUpp()
        use pm_matrixInv, only: setMatInv, choLow, choUpp
        use pm_matrixChol, only: setMatChol
        integer(IK) :: info
        do itry = 1, ntry
            call setMatrix()
            call setMatChol(mat(:,2:rank+1), uppDia, info, mat(:,1:rank), transHerm)
            if (info /= 0_IK) error stop
            call setMatInv(mat(:,2:rank+1), mat(:,1:rank), choLow)
            !dumm = dumm + mat(rank,rank) + mat(rank-1,rank-1)
        end do
    end subroutine
 
    subroutine setMatInvLUP()
        use pm_matrixLUP, only: setMatLUP
        use pm_matrixInv, only: setMatInv
        integer(IK), parameter :: offset = 1
        integer(IK) :: info
        do itry = 1, ntry
            call setMatrix()
            call setMatLUP(mat(:,2:rank+1), rperm, info)
            if (info /= 0_IK) error stop
            call setMatInv(inv, mat(:,2:rank+1), rperm)
            !dumm = dumm + mat(rank,rank) + mat(rank-1,rank-1)
        end do
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ",")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

1. The procedures under the generic interface setMatInv use an unblocked approach to computing the matrix inverse.
   However, specifying an upper-triangular Cholesky factor along with lower-triangle for the matrix inverse can potentially result in faster calculations as all matrix operations within the algorithm become column-major meaning that all memory access become local.
   

Test:

test_pm_matrixInv

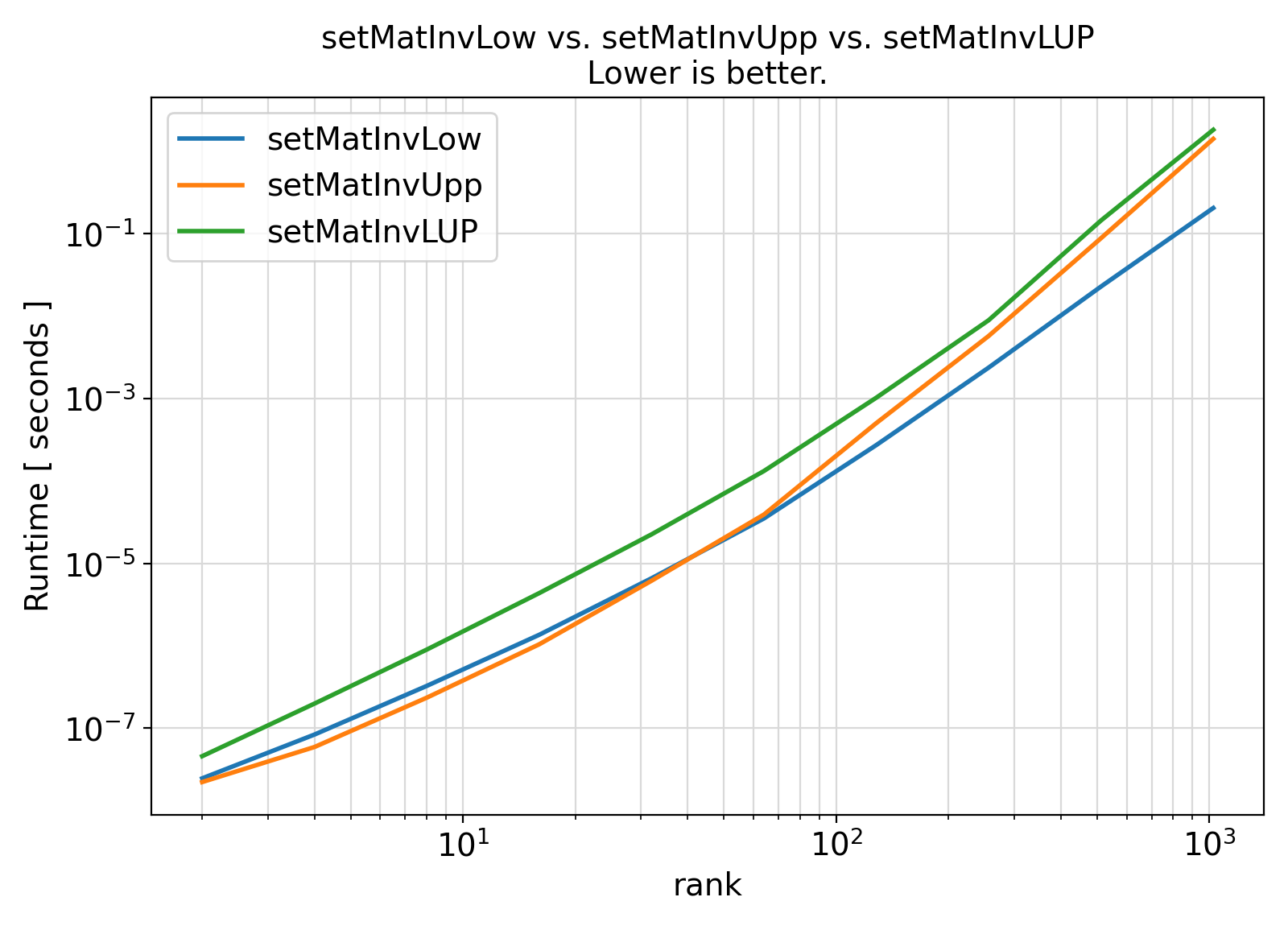
Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, September 1, 2017, 12:00 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Variable Documentation

inversion

type(inversion_type), parameter pm_matrixInv::inversion = inversion_type()

This is a scalar parameter object of type inversion_type that is exclusively used to request no transpose of a given matrix within an interface of a procedure of the ParaMonte library.

For example usage, see the documentation of the target procedure requiring this object.

See also

nothing
trans

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, September 1, 2017, 12:00 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 277 of file pm_matrixInv.F90.

MODULE_NAME

character(*,SK), parameter pm_matrixInv::MODULE_NAME = "@pm_matrixInv"

Definition at line 231 of file pm_matrixInv.F90.