pm_matrixChol Module Reference

This module contains procedures and generic interfaces for computing the Cholesky factorization of positive definite matrices.
More...

Data Types
interface	getMatChol
	Generate and return the upper or the lower Cholesky factorization of the input symmetric positive-definite matrix represented by the upper-triangle of the input argument \(\ms{mat} = L.L^T\). More...
interface	setChoLow
	[LEGACY code] Return the lower-triangle of the Cholesky factorization \(L\) of the symmetric positive-definite real-valued matrix represented by the upper-triangle of the input argument \(\ms{mat} = L.L^T\). More...
interface	setMatChol
	Compute and return the lower/upper-triangle of the Cholesky factorization \(L\) of the input Symmetric/Hermitian positive-definite triangular matrix. More...

Variables
character(*, SK), parameter	MODULE_NAME = "@pm_matrixChol"

Detailed Description

This module contains procedures and generic interfaces for computing the Cholesky factorization of positive definite matrices.

Quick start

The recommended routines for computing the Cholesky factorization are the procedures under the generic interface setChoLow() with assumed-shape dummy arguments.
The explicit-shape procedures are not recommended as the array bounds cannot be checked and the return of error status for the Cholesky factorization failure is implicit (via the first element of the output argument dia).

Cholesky factorization

In linear algebra, the Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose.
It was discovered by André-Louis Cholesky for real matrices, and posthumously published in 1924.

Algorithmic efficiency

When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition for solving systems of linear equations.

Definition

The Cholesky decomposition of a Hermitian positive-definite matrix \(A\) is a decomposition of the form,

\begin{equation} \mathbf{A} = \mathbf{LL}^{*} ~, \end{equation}

where \(L\) is a lower triangular matrix with real and positive diagonal entries, and \(L*\) denotes the conjugate transpose of \(L\).
Every Hermitian positive-definite matrix (and thus also every real-valued symmetric positive-definite matrix) has a unique Cholesky decomposition.
The converse holds trivially: if A can be written as \(LL*\) for some invertible \(L\), lower triangular or otherwise, then \(A\) is Hermitian and positive definite.
When \(A\) is a real matrix (hence symmetric positive-definite), the factorization may be written as,

\begin{equation} \mathbf{A} = \mathbf{LL}^{\mathsf{T}} ~, \end{equation}

where \(L\) is a real lower triangular matrix with positive diagonal entries.

Algorithm

For complex Hermitian matrix, the following formula applies

\begin{eqnarray} L_{j,j} &=& \sqrt{A_{j,j} - \sum_{k=1}^{j-1}L_{j,k}^{*}L_{j,k}} ~, \\ L_{i,j} &=& \frac{1}{L_{j,j}} \left(A_{i,j} - \sum_{k=1}^{j-1}L_{j,k}^{*}L_{i,k}\right) \quad {\text{for }} i > j ~. \end{eqnarray}

Therefore, the computation of the entry \((i, j)\) depends on the entries to the left and above.
The computation is usually arranged in either of the following orders:

1. The Cholesky–Banachiewicz algorithm (row-major) starts from the upper left corner of the matrix L and proceeds to calculate the matrix row by row:
   

   do i = 1, size(A,1)
       L(i,i) = sqrt(A(i,i) - dot_product(L(i,1:i-1), L(i,1:i-1)))
       L(i+1:,i) = (A(i+1:,i) - matmul(conjg(L(i,1:i-1)), L(i+1:,1:i-1))) / L(i,i)
   end do

2. The Cholesky–Crout algorithm starts from the upper left corner of the matrix L and proceeds to calculate the matrix column by column:
   

   do i = 1, size(A,1)
       L(i,i) = sqrt(A(i,i) - dot_product(L(1:i-1,i), L(1:i-1,i)))
       L(i,i+1:) = (A(i,i+1:) - matmul(conjg(L(1:i-1,i)), L(1:i-1,i+1:))) / L(i,i)
   end do

Either pattern of access allows the entire computation to be performed in-place if desired.
Given that Fortran is a column-major language, the Cholesky–Crout algorithm algorithm can potentially be faster on the contemporary hardware.
This means that the computations can be done more efficiently if one uses the upper-diagonal triangle of a Hermitian matrix to compute the corresponding upper-diagonal triangular Cholesky factorization.

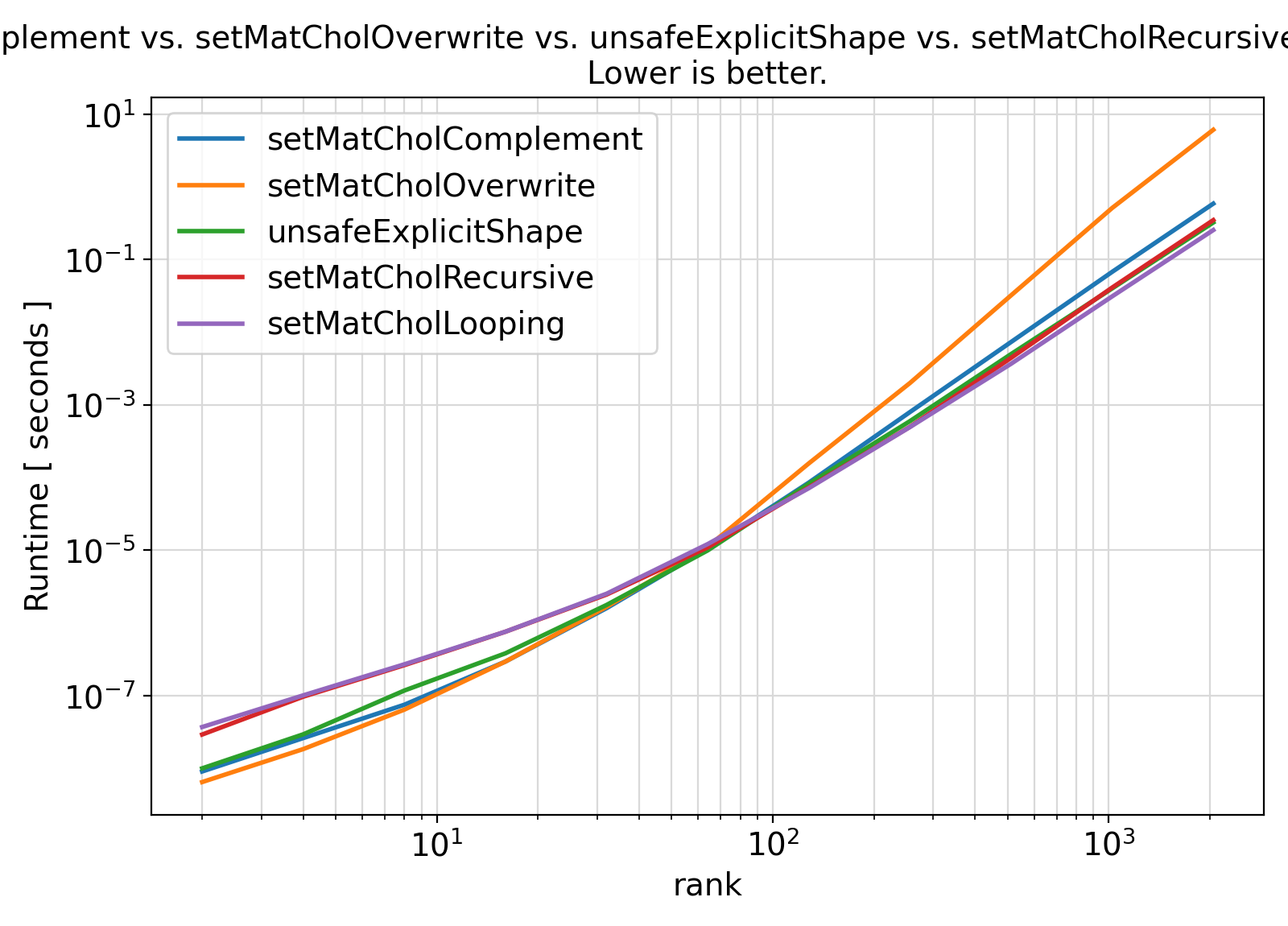
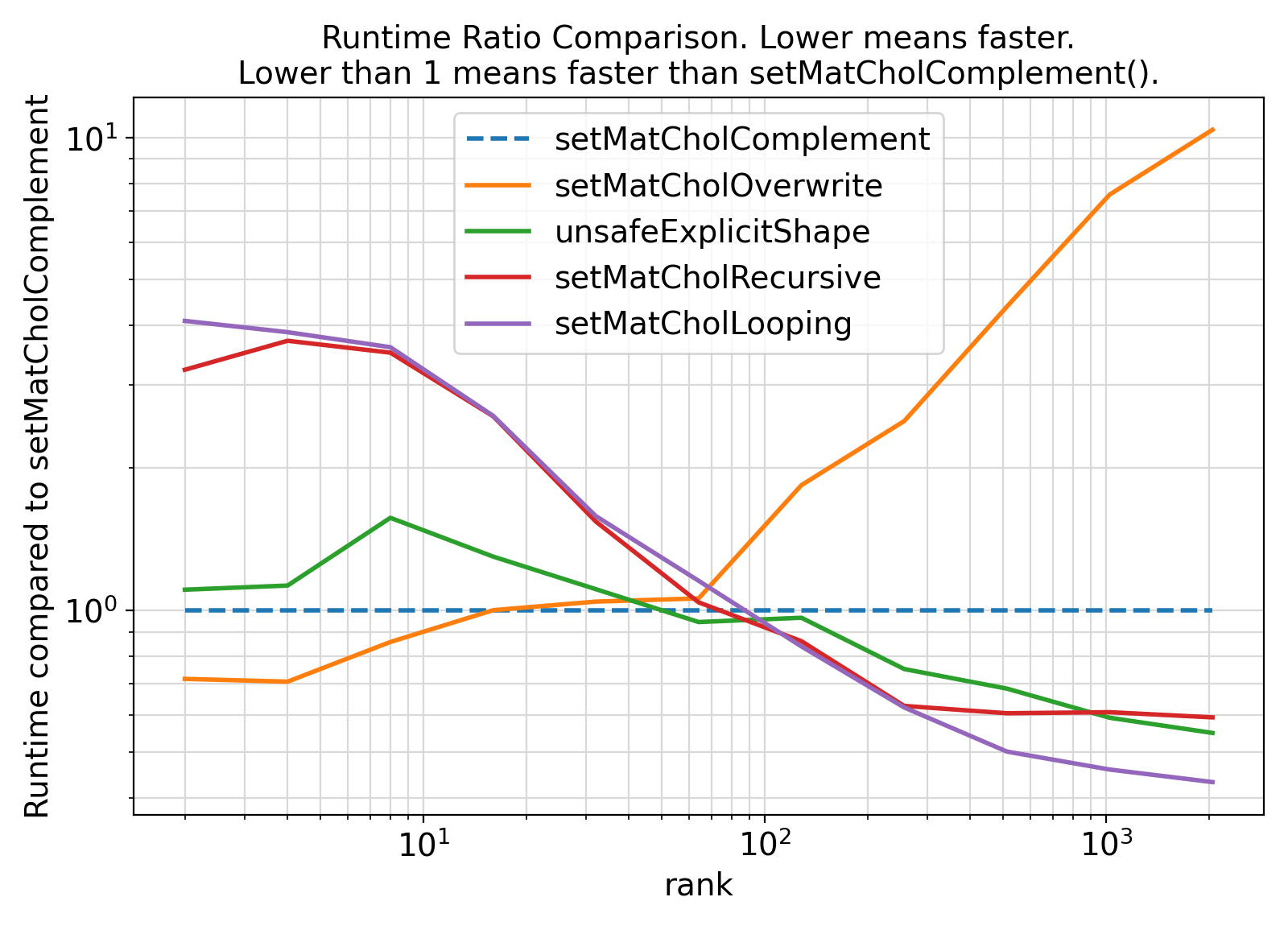
Benchmarks:

Benchmark :: Cholesky factorization - assumed-shape vs. explicit-shape dummy arguments ⛓

Here is a code snippet to compare the performances of the Cholesky factorization routine setChoLow() via two different interfaces:

1. Assumed-shape dummy arguments with explicit return of failure error flag (recommended).
2. Explicit-shape dummy arguments with implicit return of failure error flag (not recommended).

Overall, no significant difference between the two approaches is observed, meaning that the safe interface with assumed-shape arrays is much better to use.

! Test the performance of Cholesky factorization computation using an assumed-shape interface vs. explicit-shape interface.
program benchmark
 
    use pm_kind, only: IK, LK, RKG => RKD, SK
    use pm_matrixChol, only: lowDia_type, uppDia_type
    use pm_matrixChol, only: subset_type => lowDia_type!uppDia_type
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: itry, ntry
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK)     , parameter         :: NARR = 11_IK
    real(RKG)       , allocatable       :: mat(:,:), choDia(:)
    type(bench_type), allocatable       :: bench(:)
    integer(IK)     , parameter         :: nsim = 2**NARR
    integer(IK)                         :: rank
    type(subset_type), parameter        :: subset = subset_type()
    integer(IK)                         :: offset
   !real(RKG)                           :: dumm
    offset = merge(1, 0, same_type_as(subset, lowDia_type()))
 
    bench = [ bench_type(name = SK_"setMatCholComplement", exec = setMatCholComplement, overhead = setOverhead) &
            , bench_type(name = SK_"setMatCholOverwrite", exec = setMatCholOverwrite, overhead = setOverhead) &
            , bench_type(name = SK_"unsafeExplicitShape", exec = unsafeExplicitShape, overhead = setOverhead) &
            , bench_type(name = SK_"setMatCholRecursive", exec = setMatCholRecursive, overhead = setOverhead) &
            , bench_type(name = SK_"setMatCholLooping", exec = setMatCholLooping, overhead = setOverhead) &
#if         LAPACK_ENABLED
            , bench_type(name = SK_"lapack_dpotrf", exec = lapack_dpotrf, overhead = setOverhead) &
#endif
            ]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "assumed-shape vs. explicit-shape setChoLow()."
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "rank", (bench(i)%name, i = 1, size(bench))
 
        !dumm = 0._RKG
        loopOverMatrixSize: do iarr = 1, NARR
 
            rank = 2**iarr
            ntry = nsim / rank
            allocate(mat(rank, 0 : rank), choDia(rank))
            write(*,"(*(g0,:,' '))") "Benchmarking setChoLow() algorithms with array size", rank, ntry
 
            do i = 1, size(bench)
                bench(i)%timing = bench(i)%getTiming()
            end do
 
            write(fileUnit,"(*(g0,:,','))") rank, (bench(i)%timing%mean / ntry, i = 1, size(bench))
            deallocate(mat, choDia)
 
        end do loopOverMatrixSize
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        do itry = 1, ntry
            call getMatrix()
        end do
    end subroutine
 
    subroutine getMatrix()
        integer(IK) :: i
        call random_number(mat)
        mat = mat * 1.e-5_RKG
        do i = 1, size(mat, dim = 1, kind = IK)
            mat(i, i - offset) = 1._RKG ! lowDia
           !mat(i, i) = 1._RKG ! uppDia
        end do
    end subroutine
 
#if LAPACK_ENABLED
    subroutine lapack_dpotrf()
        integer(IK) :: info
        do itry = 1, ntry
            call getMatrix()
            call dpotrf("U", rank, mat(1,1), rank, info)
            if (info /= 0_IK) error stop
        end do
    end subroutine
#endif
 
    subroutine unsafeExplicitShape()
        use pm_matrixChol, only: setChoLow
        logical(LK) :: failed
        do itry = 1, ntry
            call getMatrix()
            call setChoLow(mat(:,1-offset:rank-offset), choDia, rank)
            if (choDia(1) < 0._RKG) error stop
        end do
    end subroutine
 
    subroutine setMatCholOverwrite()
        use pm_matrixChol, only: setMatChol, nothing
        integer(IK) :: info
        do itry = 1, ntry
            call getMatrix()
            call setMatChol(mat(:,1-offset:rank-offset), subset, info, mat(:,1-offset:rank-offset), nothing)
            if (info /= 0_IK) error stop
        end do
    end subroutine
 
    subroutine setMatCholComplement()
        use pm_matrixChol, only: setMatChol, transHerm
        integer(IK) :: info
        do itry = 1, ntry
            call getMatrix()
           !call setMatChol(mat(:,0:rank-1), subset, info, mat(:,1:rank), transHerm)
            call setMatChol(mat(:,1-offset:rank-offset), subset, info, mat(:,offset:rank), transHerm)
            if (info /= 0_IK) error stop
        end do
    end subroutine
 
    subroutine setMatCholLooping()
        use pm_matrixChol, only: setMatChol, iteration
        integer(IK) :: info
        do itry = 1, ntry
            call getMatrix()
            call setMatChol(mat(:,1-offset:rank-offset), subset, info, iteration)
            if (info /= 0_IK) error stop
        end do
    end subroutine
 
    subroutine setMatCholRecursive()
        use pm_matrixChol, only: setMatChol, recursion
        integer(IK) :: info
        do itry = 1, ntry
            call getMatrix()
            call setMatChol(mat(:,1-offset:rank-offset), subset, info, recursion)
            if (info /= 0_IK) error stop
        end do
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ",")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Todo:

High Priority: A benchmark comparing the performance of the two computational algorithms above should be implemented and gauge the impact of row vs. column major access pattern.

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, Friday 1:54 AM, April 21, 2017, Institute for Computational Engineering and Sciences (ICES), The University of Texas, Austin, TX

Variable Documentation

MODULE_NAME

character(*, SK), parameter pm_matrixChol::MODULE_NAME = "@pm_matrixChol"

Definition at line 149 of file pm_matrixChol.F90.