
|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |

|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
This module contains relevant mathematical constants. More...
Data Types | |
| type | ninf_type |
| This is the indicator type for generating instances of objects that indicate the use of the negative infinity -\infty as an input argument to the generic interfaces of the ParaMonte library. More... | |
| type | origin_type |
| This is the derived type origin_type representing the geometric origin of the coordinates. More... | |
| type | pinf_type |
| This is the indicator type for generating instances of objects that indicate the use of the positive infinity +\infty as an input argument to the generic interfaces of the ParaMonte library. More... | |
Variables | |
| character(*, SK), parameter | MODULE_NAME = "@pm_mathConst" |
| real(RKB), parameter | PI = acos(-1._RKB) |
The scalar real constant of kind with highest available precision RKB representing the irrational number \pi. More... | |
| real(RKB), parameter | TWO_PI = 2 * PI |
The scalar real constant of kind with highest available precision RKB representing twice the irrational number \pi. More... | |
| real(RKB), parameter | HALF_PI = .5_RKB * PI |
The scalar real constant of kind with highest available precision RKB representing half the irrational number \pi. More... | |
| real(RKB), parameter | INVERSE_PI = 1._RKB / PI |
The scalar real constant of kind with highest available precision RKB representing the inverse of the irrational number \pi. More... | |
| real(RKB), parameter | QUARTER_PI = .25_RKB * PI |
The scalar real constant of kind with highest available precision RKB representing a quarter of the irrational number \pi. More... | |
| real(RKB), parameter | LOG_PI = log(PI) |
The scalar real constant of kind with highest available precision RKB representing \log(\pi). More... | |
| real(RKB), parameter | SQRT_PI = sqrt(PI) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{\pi}. More... | |
| real(RKB), parameter | LOG_TWO_PI = log(TWO_PI) |
The scalar real constant of kind with highest available precision RKB representing \log(2\pi). More... | |
| real(RKB), parameter | SQRT_TWO_PI = sqrt(TWO_PI) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{2\pi}. More... | |
| real(RKB), parameter | SQRT_HALF_PI = sqrt(HALF_PI) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{\frac{\pi}{2}}. More... | |
| real(RKB), parameter | INVERSE_SQRT_PI = sqrt(INVERSE_PI) |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\sqrt{\pi}}. More... | |
| real(RKB), parameter | INVERSE_SQRT_TWO_PI = 1._RKB / SQRT_TWO_PI |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\sqrt{2\pi}}. More... | |
| real(RKB), parameter | LOG_INVERSE_SQRT_TWO_PI = log(INVERSE_SQRT_TWO_PI) |
The scalar real constant of kind with highest available precision RKB representing \log\left(\frac{1}{\sqrt{2\pi}}\right), frequently appearing in distributions (e.g., Normal). More... | |
| real(RKB), parameter | NAPIER = exp(1._RKB) |
The scalar real constant of kind with highest available precision RKB representing the Napier constant (a.k.a. Euler number) e = \exp(1). More... | |
| real(RKB), parameter | LOG_TWO = log(2._RKB) |
The scalar real constant of kind with highest available precision RKB representing \log(2). More... | |
| real(RKB), parameter | LOG_TEN = log(1.e1_RKB) |
The scalar real constant of kind with highest available precision RKB representing \log(10). More... | |
| real(RKB), parameter | LOG_HALF = log(0.5_RKB) |
The scalar real constant of kind with highest available precision RKB representing \log\left(\frac{1}{2}\right). More... | |
| real(RKB), parameter | SQRT_TWO = sqrt(2._RKB) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{2}. More... | |
| real(RKB), parameter | LOG10_NAPIER = log10(NAPIER) |
The scalar real constant of kind with highest available precision RKB representing \log_{10}(e). More... | |
| real(RKB), parameter | INVERSE_LOG_TWO = 1._RKB / LOG_TWO |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\log(2)}. More... | |
| real(RKB), parameter | INVERSE_SQRT_TWO = 1._RKB / SQRT_TWO |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\sqrt{2}}. More... | |
| type(origin_type), parameter | ORIGIN = origin_type() |
| The scalar constant object of type origin_type representing the geometric origin of the coordinates. More... | |
| real(RKB), parameter | EULER_CONST = 0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749_RKB |
The scalar real constant of kind with highest available precision RKB representing the Euler-Mascheroni constant. More... | |
| real(RKB), parameter | APERY_CONST = 1.20205690315959428539973816151144999076498629234049888179227155534183820578631309018645587360933525814619915_RKB |
The scalar real constant of kind with highest available precision RKB representing the Apery constant. More... | |
| real(RKB), parameter | PRIME_CONST = .414682509851111660248109622154307708365774238137916977868245414488640960619357334196290048428475777939616_RKB |
The scalar real constant of kind with highest available precision RKB representing the irrational Prime constant. More... | |
| real(RKB), parameter | GOLDEN_RATIO = .5_RKB * (1._RKB + sqrt(5._RKB)) |
The scalar real constant of kind with highest available precision RKB representing the Golden Ratio constant. More... | |
| real(RKB), parameter | SILVER_RATIO = 1._RKB + sqrt(2._RKB) |
The scalar real constant of kind with highest available precision RKB representing the Silver Ratio constant. More... | |
| real(RKB), parameter | SUPER_GOLDEN_RATIO = (2._RKB * cosh(acosh(29._RKB / 2._RKB) / 3._RKB) + 1._RKB) / 3._RKB |
The scalar real constant of kind with highest available precision RKB representing the Supergolden Ratio constant.More... | |
| type(ninf_type), parameter | ninf = ninf_type() |
| The scalar constant object of type ninf_type that indicates the use of the negative infinity -\infty as an input argument to the generic interfaces of the ParaMonte library. More... | |
| type(pinf_type), parameter | pinf = pinf_type() |
| The scalar constant object of type pinf_type that indicates the use of the positive infinity +\infty as an input argument to the generic interfaces of the ParaMonte library. More... | |
This module contains relevant mathematical constants.
real precision kind.real kinds, simply convert the numbers to the desired kind via the Fortran intrinsic real(x, kind = RKG) where RKG refers to the target kind parameter used in the expression.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
| real(RKB), parameter pm_mathConst::APERY_CONST = 1.20205690315959428539973816151144999076498629234049888179227155534183820578631309018645587360933525814619915_RKB |
The scalar real constant of kind with highest available precision RKB representing the Apery constant.
In mathematics, Apéry's constant is the sum of the reciprocals of the positive cubes. That is, it is defined as the number
\begin{equation} \begin{aligned} \zeta(3) &= \sum _{n=1}^{\infty} \frac{1}{n^{3}} \\ &= \lim _{n\to\infty} \left( {\frac{1}{1^{3}}} + {\frac {1}{2^{3}}} + \cdots + {\frac{1}{n^{3}}} \right) ~, \end{aligned} \end{equation}
where \zeta is the Riemann zeta function.
It has an approximate value of,
\begin{equation} \zeta(3) = 1.202056903159594285399738161511449990764986292\ldots ~. \end{equation}
The constant is named after Roger Apéry.
It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics.
It also arises in the analysis of random minimum spanning trees and in conjunction with the Gamma function when solving certain integrals involving exponential functions in a quotient.
These appear occasionally in physics, for instance, when evaluating the two-dimensional case of the Debye model and the Stefan–Boltzmann law.
109 significant digits.use pm_sampleCov, only: getCovMerged kinds surpasses the number of decimal digits hardcoded here.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 222 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::EULER_CONST = 0.577215664901532860606512090082402431042159335939923598805767234884867726777664670936947063291746749_RKB |
The scalar real constant of kind with highest available precision RKB representing the Euler-Mascheroni constant.
The Euler constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter \gamma. It is defined as the limiting difference between the harmonic series and the natural logarithm,
\begin{equation} \begin{aligned} \gamma &= \lim _{n \to \infty} \left( -\log(n) + \sum _{k=1}^{n} \frac{1}{k} \right) \\ &= \int _{1}^{\infty} \left( -\frac{1}{x} + \frac{1}{\lfloor x \rfloor} \right) ~ dx ~. \end{aligned} \end{equation}
Here, \lfloor x \rfloor represents the Fortran intrinsic floor() function.

Applications
The Euler constant appears in many areas of science, including,
99 significant digits.use pm_sampleCov, only: getCovMerged kinds surpasses the number of decimal digits hardcoded here.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 189 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::GOLDEN_RATIO = .5_RKB * (1._RKB + sqrt(5._RKB)) |
The scalar real constant of kind with highest available precision RKB representing the Golden Ratio constant.
In mathematics, two quantities are in the Golden Ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities.
Expressed algebraically, for quantities a and b with 0 < a < b,
\begin{equation} \frac{a + b}{a} = \frac{a}{b} = \phi ~, \end{equation}
where the Greek letter \phi denotes the Golden Ratio.
The constant \phi satisfies the quadratic equation \phi^{2} = \phi + 1 and is an irrational number with a value of,
\begin{equation} \phi = \frac{1 + \sqrt{5}}{2} = 1.618033988749\ldots ~. \end{equation}
The Golden Ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, among other names.
Mathematicians have studied the properties of the Golden Ratio since antiquity.
It is the ratio of a diagonal of a regular pentagon to its side and thus appears in the construction of the dodecahedron and icosahedron.
A golden rectangle — that is, a rectangle with an aspect ratio of \phi — may be cut into a square and a smaller rectangle with the same aspect ratio.
The Golden Ratio has been used to analyze the proportions of natural objects and artificial systems such as financial markets, in some cases based on dubious fits to data.
The Golden Ratio appears in some patterns in nature, including the spiral arrangement of leaves and other parts of vegetation.
Some 20th-century artists and architects, including Le Corbusier and Salvador Dalí, have proportioned their works to approximate the Golden Ratio, believing it to be aesthetically pleasing.
These usages frequently appear in the form of a golden rectangle, as illustrated below.
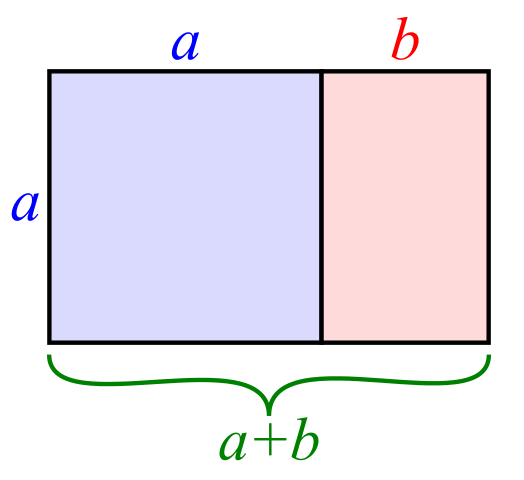
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 283 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::HALF_PI = .5_RKB * PI |
The scalar real constant of kind with highest available precision RKB representing half the irrational number \pi.
Definition at line 50 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::INVERSE_LOG_TWO = 1._RKB / LOG_TWO |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\log(2)}.
Definition at line 72 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::INVERSE_PI = 1._RKB / PI |
The scalar real constant of kind with highest available precision RKB representing the inverse of the irrational number \pi.
Definition at line 51 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::INVERSE_SQRT_PI = sqrt(INVERSE_PI) |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\sqrt{\pi}}.
Definition at line 58 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::INVERSE_SQRT_TWO = 1._RKB / SQRT_TWO |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\sqrt{2}}.
Definition at line 73 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::INVERSE_SQRT_TWO_PI = 1._RKB / SQRT_TWO_PI |
The scalar real constant of kind with highest available precision RKB representing \frac{1}{\sqrt{2\pi}}.
Definition at line 59 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG10_NAPIER = log10(NAPIER) |
The scalar real constant of kind with highest available precision RKB representing \log_{10}(e).
Definition at line 71 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG_HALF = log(0.5_RKB) |
The scalar real constant of kind with highest available precision RKB representing \log\left(\frac{1}{2}\right).
Definition at line 69 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG_INVERSE_SQRT_TWO_PI = log(INVERSE_SQRT_TWO_PI) |
The scalar real constant of kind with highest available precision RKB representing \log\left(\frac{1}{\sqrt{2\pi}}\right), frequently appearing in distributions (e.g., Normal).
Definition at line 60 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG_PI = log(PI) |
The scalar real constant of kind with highest available precision RKB representing \log(\pi).
Definition at line 53 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG_TEN = log(1.e1_RKB) |
The scalar real constant of kind with highest available precision RKB representing \log(10).
Definition at line 68 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG_TWO = log(2._RKB) |
The scalar real constant of kind with highest available precision RKB representing \log(2).
Definition at line 67 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::LOG_TWO_PI = log(TWO_PI) |
The scalar real constant of kind with highest available precision RKB representing \log(2\pi).
Definition at line 55 of file pm_mathConst.F90.
| character(*,SK), parameter pm_mathConst::MODULE_NAME = "@pm_mathConst" |
Definition at line 42 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::NAPIER = exp(1._RKB) |
The scalar real constant of kind with highest available precision RKB representing the Napier constant (a.k.a. Euler number) e = \exp(1).
Definition at line 66 of file pm_mathConst.F90.
The scalar constant object of type ninf_type that indicates the use of the negative infinity -\infty as an input argument to the generic interfaces of the ParaMonte library.
See the documentations of the generic interfaces that use this constant for example usage.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 423 of file pm_mathConst.F90.
| type(origin_type), parameter pm_mathConst::ORIGIN = origin_type() |
The scalar constant object of type origin_type representing the geometric origin of the coordinates.
For example usage, see the corresponding PaaMonte generic interfaces that use this object.
The origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space.
In physical problems, the choice of origin is often arbitrary, meaning any choice of origin will ultimately give the same answer.
This allows one to pick an origin point that makes the mathematics as simple as possible, often by taking advantage of some kind of geometric symmetry.
In a Cartesian coordinate system, the origin is the point where the axes of the system intersect.
The origin divides each of these axes into two halves, a positive and a negative semiaxis.
Points can then be located with reference to the origin by giving their numerical coordinates—that is, the positions of their projections along each axis, either in the positive or negative direction.
The coordinates of the origin are always all zero, for example (0,0) in two dimensions and (0,0,0) in three.
The origin of the complex plane can be referred as the point where real axis and imaginary axis intersect each other.
In other words, the origin in the complex plane is the complex number zero.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 131 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::PI = acos(-1._RKB) |
The scalar real constant of kind with highest available precision RKB representing the irrational number \pi.
Definition at line 48 of file pm_mathConst.F90.
The scalar constant object of type pinf_type that indicates the use of the positive infinity +\infty as an input argument to the generic interfaces of the ParaMonte library.
See the documentations of the generic interfaces that use this constant for example usage.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 470 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::PRIME_CONST = .414682509851111660248109622154307708365774238137916977868245414488640960619357334196290048428475777939616_RKB |
The scalar real constant of kind with highest available precision RKB representing the irrational Prime constant.
The prime constant is the real number \rho whose nth binary digit is 1 if n is prime and 0 if n is composite or 1.
In other words, \rho is the number whose binary expansion corresponds to the indicator function of the set of prime numbers.
That is,
\begin{equation} \rho = \sum_{p} \frac{1}{2^{p}} = \sum_{n = 1}^{\infty} \frac{\chi_{\mathbb{P}}(n)}{2^{n}} \rho = \sum_{{p}} \frac{1}{2^{p}} = \sum_{{n = 1}}^{\infty} \frac{\chi_{{{\mathbb{P}}}}(n)}{2^{n}} ~, \end{equation}
where p indicates a prime and \chi_{{{\mathbb{P}}}} is the characteristic function of the set \mathbb{P} of prime numbers.
The beginning of the decimal expansion of \rho is: \rho = 0.414682509851111660248109622\ldots.
105 significant digits.use pm_sampleCov, only: getCovMerged kinds surpasses the number of decimal digits hardcoded here.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 246 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::QUARTER_PI = .25_RKB * PI |
The scalar real constant of kind with highest available precision RKB representing a quarter of the irrational number \pi.
Definition at line 52 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::SILVER_RATIO = 1._RKB + sqrt(2._RKB) |
The scalar real constant of kind with highest available precision RKB representing the Silver Ratio constant.
In mathematics, two quantities are in the Silver Ratio (or silver mean) if the ratio of the smaller of those two quantities to the larger quantity is the same as the ratio of the larger quantity to the sum of the smaller quantity and twice the larger quantity.
This defines the Silver Ratio as an irrational mathematical constant, whose value of one plus the square root of 2 is approximately 2.4142135623.
Its name is an allusion to the Golden Ratio.
Analogously to the way the Golden Ratio is the limiting ratio of consecutive Fibonacci numbers, the Silver Ratio is the limiting ratio of consecutive Pell numbers.
The Silver Ratio is denoted by \delta_S, which can be expressed algebraically as,
\begin{equation} \frac {2a+b}{a} = \frac {a}{b} \equiv \delta _{S} ~, \end{equation}
or equivalently,
\begin{equation} 2 + \frac {b}{a} = {\frac {a}{b}} \equiv \delta _{S} ~. \end{equation}
The Silver Ratio can also be defined by the simple continued fraction [2; 2, 2, 2, ...],
\begin{equation} 2 + {\cfrac{1}{2 + {\cfrac{1}{2 + {\cfrac{1}{2 + \ddots}}}}}} = \delta _{S} ~. \end{equation}
The convergents of this continued fraction are ratios of consecutive Pell numbers.
These fractions provide accurate rational approximations of the Silver Ratio, analogous to the approximation of the Golden Ratio by ratios of consecutive Fibonacci numbers.
The Silver Rectangle is connected to the regular octagon.
If a regular octagon is partitioned into two isosceles trapezoids and a rectangle, then the rectangle is a Silver Rectangle with an aspect ratio of 1:\delta_S.
The four sides of the trapezoids are in a ratio of 1:1:1:\delta_S.
If the edge length of a regular octagon is t, then the span of the octagon (the distance between opposite sides) is \delta_{S}t, and the area of the octagon is 2\delta_{S}t^2.
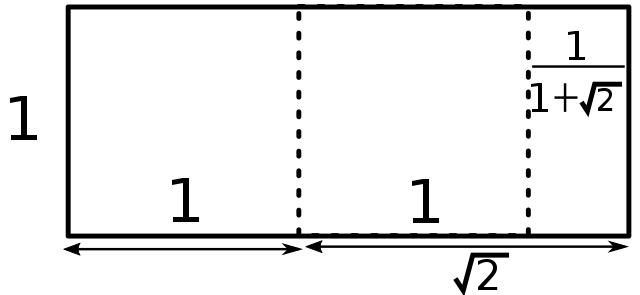

Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 329 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::SQRT_HALF_PI = sqrt(HALF_PI) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{\frac{\pi}{2}}.
Definition at line 57 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::SQRT_PI = sqrt(PI) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{\pi}.
Definition at line 54 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::SQRT_TWO = sqrt(2._RKB) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{2}.
Definition at line 70 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::SQRT_TWO_PI = sqrt(TWO_PI) |
The scalar real constant of kind with highest available precision RKB representing \sqrt{2\pi}.
Definition at line 56 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::SUPER_GOLDEN_RATIO = (2._RKB * cosh(acosh(29._RKB / 2._RKB) / 3._RKB) + 1._RKB) / 3._RKB |
The scalar real constant of kind with highest available precision RKB representing the Supergolden Ratio constant.
In mathematics, two quantities are in the superGolden Ratio if the quotient of the larger number divided by the smaller one is equal to
\begin{equation} \psi = {\frac{1 + {\sqrt[{3}]{\frac{29 + 3{\sqrt{93}}}{2}}} + {\sqrt[{3}]{\frac{29 - 3{\sqrt{93}}}{2}}}}{3}} ~, \end{equation}
which is the only real solution to the equation x^{3} = x^{2} + 1.
It can also be represented using the hyperbolic cosine as,
\begin{equation} \psi = \frac{2}{3} \cosh{\left( \tfrac{\cosh^{-1} \left(\frac{29}{2} \right)}{3} \right)} + \frac {1}{3} ~. \end{equation}
The decimal expansion of this number begins 1.465571231876768026656731\ldots, and the ratio is commonly represented by the Greek letter \psi.
Many of the properties of the Supergolden Ratio are related to those of the Golden Ratio.
For example, the nth item of the Narayana sequence is the number of ways to tile a 1\times n rectangle with 1\times 1 and 1\times3 tiles.
Similarly, the nth term of the Fibonacci sequence is the number of ways to tile a 1\times n rectangle with 1\times1 and 1\times2 tiles.
The Supergolden Ratio satisfies \psi -1 = \psi^{-2}, while the Golden Ratio satisfies \phi -1 = \phi^{-1}.
In the Fibonacci Rabbit Problem, each pair breeds each cycle starting after two cycles, while in the Narayana Cow Problem, each pair breeds each cycle starting after three cycles.
There is a Supergolden Rectangle that has the property that if a square is removed from one side, the remaining rectangle can be divided into two Supergolden Rectangles of opposite orientations.
A Supergolden Rectangle is a rectangle whose side lengths are in the Supergolden Ratio, i.e. the length of the longer side divided by the length of the shorter side is equal to the Supergolden Ratio: {\frac{1 + {\sqrt[{3}]{\frac{29 + 3{\sqrt{93}}}{2}}} + {\sqrt[{3}]{\frac{29-3{\sqrt{93}}}{2}}}}{3}}.
When a square with the same side length as the shorter side of the rectangle is removed from one side of the rectangle, the sides resulting rectangle will be in a \psi^2:1 ratio.
This rectangle can be divided into rectangles with side-length ratios of \psi:1 and 1:\psi, two Supergolden Ratios of perpendicular orientations.
Their areas will be in a \psi^2:1 ratio.
In addition, if the line that separates the two Supergolden Rectangles from each other is extended across the rest of the original rectangle such that it – along with the side of the square that was removed from the original rectangle – divides the original rectangle into quadrants, then the larger Supergolden Rectangle has the same area as the opposite quadrant, its diagonal length is the length of the short side of the original rectangle divided by \sqrt{\psi}, the fourth quadrant is also a Supergolden Rectangle, and its diagonal length is \sqrt {\psi } times the length of the short side of the original rectangle.

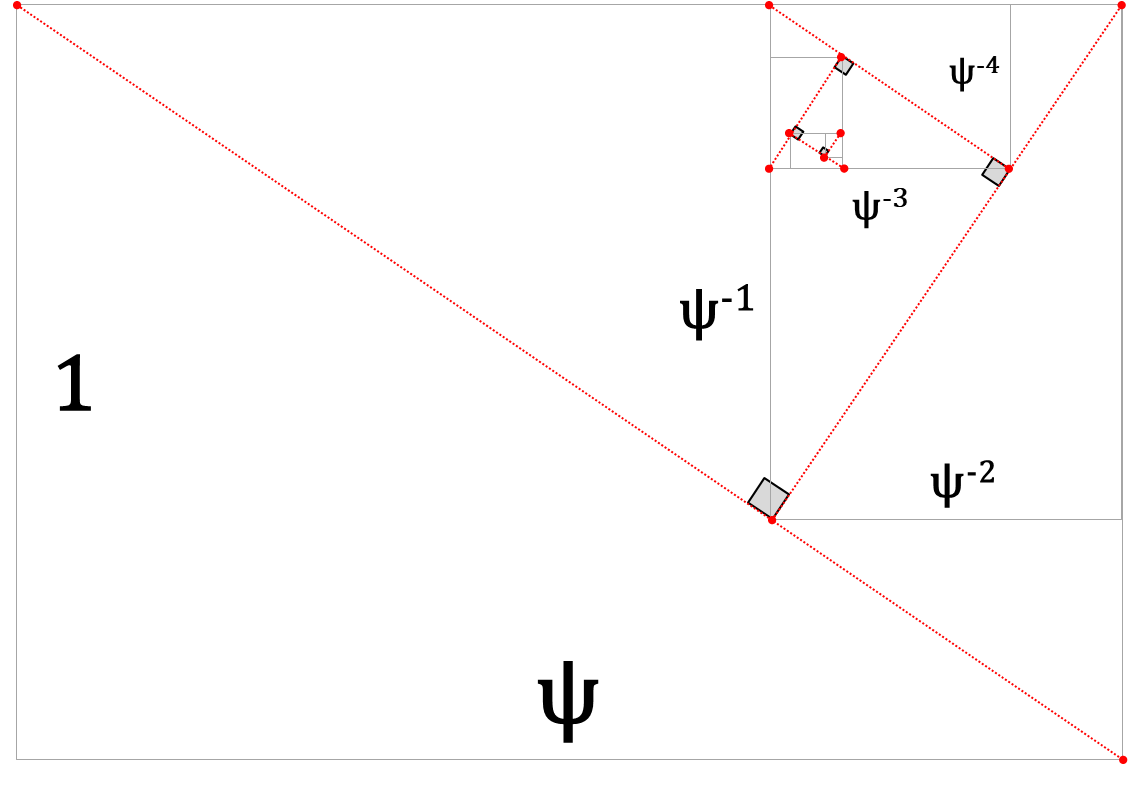
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 379 of file pm_mathConst.F90.
| real(RKB), parameter pm_mathConst::TWO_PI = 2 * PI |
The scalar real constant of kind with highest available precision RKB representing twice the irrational number \pi.
Definition at line 49 of file pm_mathConst.F90.