pm_cosmology::setVolComDiffNormed Interface Reference

Generate and return the cosmological Comoving Volume Differential (Element) per unit solid angle of the sky (i.e., 1 Steradian normalized to Hubble Volume, given the user-specified cosmological parameters. More...

Detailed Description

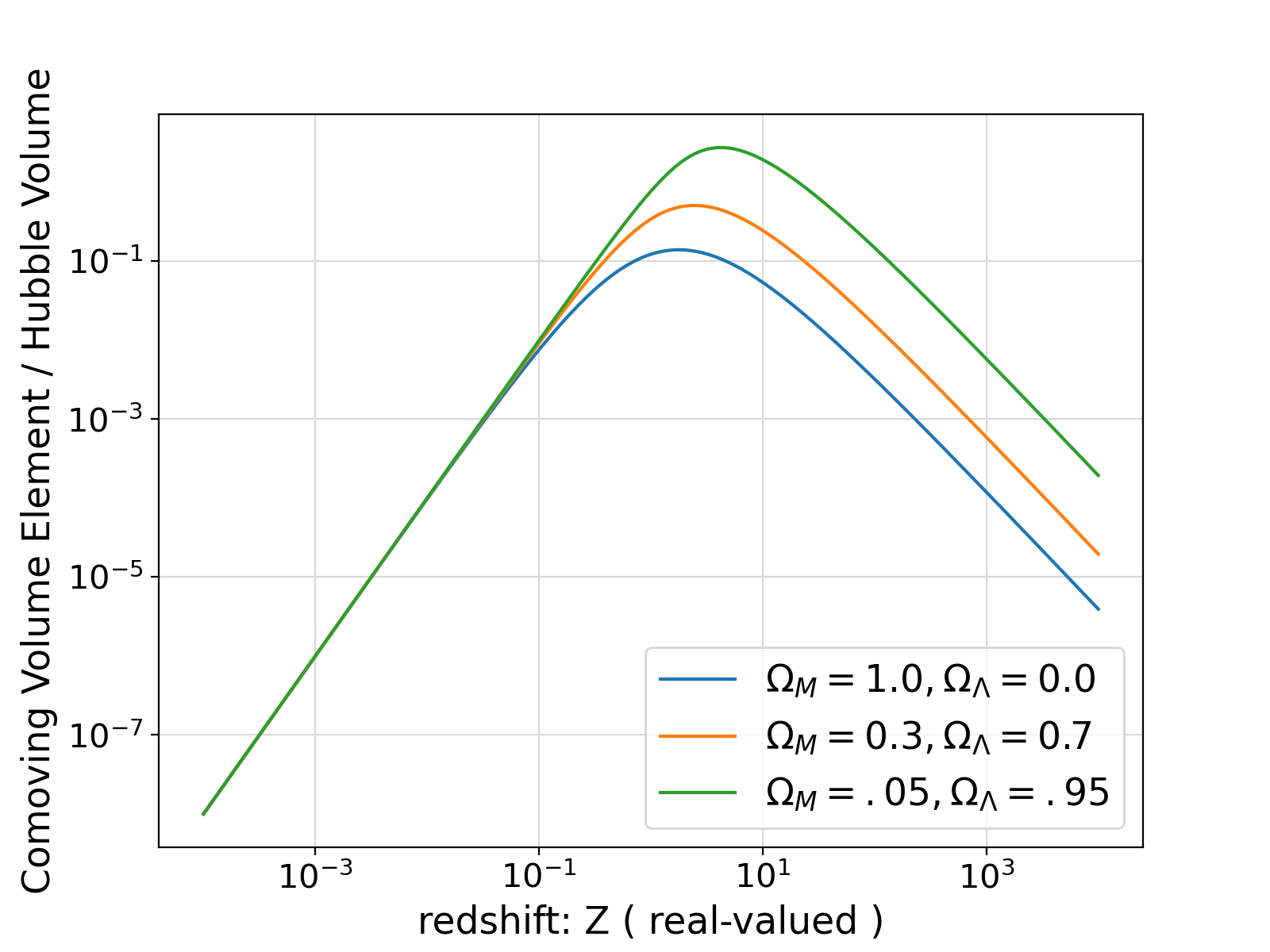
Generate and return the cosmological Comoving Volume Differential (Element) per unit solid angle of the sky (i.e., 1 Steradian normalized to Hubble Volume, given the user-specified cosmological parameters.

Assuming \((\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)\) represent the normalized densities of Dark Matter, Dark Energy, Radiation Energy, and Curvature in a Universe with negligible neutrino mass such that \(\Omega_M + \Omega_\Lambda + \Omega_R + \Omega_K = 1\), the Comoving Volume Element \(dV_C\) at a given cosmological redshift \(z\) is defined as (e.g., Peebles, 1993),

\begin{eqnarray} \large dV_C(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) &=& D_H \frac{\big[D_M(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)\big]^2}{E(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)} ~ dz ~ d\Omega ~, \\ &=& D_H \frac{\big[D_A(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)\big]^2}{E(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)} (1+z)^2 ~ dz ~ d\Omega ~, \\ &=& D_H \frac{\big[D_L(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)\big]^2}{E(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)} \frac{1}{(1+z)^2} ~ dz ~ d\Omega ~, \end{eqnarray}

where

1. \(dV_C(z; \cdots)\) is the cosmological Comoving Volume Element at redshift \(z\),,
2. \(D_M(z; \cdots)\) is the cosmological Transverse Comoving Distance as a subroutine of redshift,
3. \(D_A(z; \cdots)\) is the cosmological Angular Diameter Distance as a subroutine of redshift,
4. \(D_L(z; \cdots)\) is the cosmological Luminosity Distance as a subroutine of redshift,
5. \(E(z; \cdots)\) is the dimensionless Hubble Parameter,
6. \(D_H = \frac{C}{H_0}\) is the Hubble Distance,
7. \(H_0\) is the Hubble Constant.
8. \(C\) is the speed of light,
9. \(z\) is the redshift,

The value returned by the procedures under this generic interface is \(\frac{dV_C}{V_H}\), that is, normalized to the Hubble Volume.
To obtain the full-sky (normalized) Comoving Volume Element, multiply the output of the procedures under this generic interface by \(4\pi\), that is, 4 * acos(-1.).

Parameters

[out]	volComDiffNormed	: The output scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 containing the cosmological Comoving Volume Element per Steradian at the desired redshift normalized to the Hubble Distance.
[in]	disComTransNormedSq	: The input scalar or array of the same rank as other array-like arguments, of type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128) representing the the square of the Dimensionless (Normalized) Transverse Comoving Distance at the desired redshift for which the Comoving Volume Element must be computed. This argument can be readily obtained by taking the square of the output of getDisComTransNormed, or if the cosmology is the Concordance model, one can use the approximation provided by getDisComTransNormedWU10. See the examples below for usage.
[in]	hubbleParamNormed	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as disComTransNormedSq representing the Dimensionless Hubble Parameter at the desired redshift for which the Comoving Volume Element must be computed. This argument can be readily obtained by taking the square-root of the output of getHubbleParamNormedSq. See the examples below for usage.

Possible calling interfaces ⛓

use pm_cosmology, only: setVolComDiffNormed
 
call setVolComDiffNormed(volComDiffNormed, disComTransNormedSq, hubbleParamNormed)

Warning

The input arguments must be computed for the same redshift and cosmological parameters.
The equivalence and consistencies of the input arguments are not verified within the algorithm because such validations require extra information that is not provided as input.

Remarks

The procedures under discussion are pure.

The procedures under discussion are elemental.

The reason for requesting the rather awkward input arguments above instead of the redshift and other primitive cosmological parameters is to ensure the computation efficiency of the algorithms at the highest level by taking out the potentially unnecessary computations out of the algorithms.
See getVolComDiffNormed for an equivalent, more flexible, but potentially less performant interface.

Developer Remark:

There is no performance benefit in passing the inverse of hubbleParamNormed instead of the what is passed in the current interface.
Do not attempt to change the interface.

See also

getVolComNormed
getHubbleParamNormedSq
getDisComTransNormed
getDisLumNormed
getDisAngNormed
getDisComNormed
LOG_HUBBLE_CONST
HUBBLE_DISTANCE_MPC
HUBBLE_CONST
OMEGA_M
OMEGA_L
OMEGA_R
OMEGA_K

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK
    use pm_cosmology, only: getDisComTransNormed
    use pm_cosmology, only: getHubbleParamNormedSq
    use pm_cosmology, only: setVolComDiffNormed
    use pm_io, only: display_type
 
    implicit none
 
    real :: VolComDiffNormed(3)
    type(display_type)      :: disp
 
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!Compute the Comoving Volume Element in units of Hubble Volume.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("call setVolComDiffNormed(VolComDiffNormed(1), getDisComTransNormed(zplus1 = 1., reltol = sqrt(epsilon(0.)))**2, sqrt(getHubbleParamNormedSq(zplus1 = 1.)))")
                    call setVolComDiffNormed(VolComDiffNormed(1), getDisComTransNormed(zplus1 = 1., reltol = sqrt(epsilon(0.)))**2, sqrt(getHubbleParamNormedSq(zplus1 = 1.)))
    call disp%show("VolComDiffNormed(1)")
    call disp%show( VolComDiffNormed(1) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("call setVolComDiffNormed(VolComDiffNormed(1), getDisComTransNormed(zplus1 = 1.1, reltol = sqrt(epsilon(0.)))**2, sqrt(getHubbleParamNormedSq(zplus1 = 1.1)))")
                    call setVolComDiffNormed(VolComDiffNormed(1), getDisComTransNormed(zplus1 = 1.1, reltol = sqrt(epsilon(0.)))**2, sqrt(getHubbleParamNormedSq(zplus1 = 1.1)))
    call disp%show("VolComDiffNormed(1)")
    call disp%show( VolComDiffNormed(1) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6, reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6)))")
                    call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6, reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6)))
    call disp%show("VolComDiffNormed(1:2)")
    call disp%show( VolComDiffNormed(1:2) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.2, reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.2)))")
                    call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.2, reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.2)))
    call disp%show("VolComDiffNormed(1:2)")
    call disp%show( VolComDiffNormed(1:2) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.4, omegaK = -0.2, sqrtAbsOmegaK = sqrt(0.2), reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.4, omegaK = -0.2)))")
                    call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.4, omegaK = -0.2, sqrtAbsOmegaK = sqrt(0.2), reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.4, omegaK = -0.2)))
    call disp%show("VolComDiffNormed(1:2)")
    call disp%show( VolComDiffNormed(1:2) )
    call disp%skip()
 
    ! Generate both the cosmic rate and the rate density.
 
    block
 
        use pm_val2str, only: getStr
        use pm_arraySpace, only: getLinSpace
        use pm_arraySpace, only: getLogSpace
 
        real, allocatable   :: zplus1(:), OmegaM(:), OmegaL(:), VolComDiffNormed(:)
        integer :: fileUnit, i
 
        OmegaM = [1., 0.3, .05]
        OmegaL = 1. - OmegaM
        allocate(VolComDiffNormed, mold = OmegaM)
        zplus1 = 1. + getLogSpace(log(0.0001), log(10000.), 500_IK)
 
        open(newunit = fileUnit, file = "setVolComDiffNormed.RK.txt")
        write(fileUnit, "(*(g0,:,','))") "z", ("DisLum_"//getStr(OmegaM(i),"(g0.1)")//"_"//getStr(OmegaL(i),"(g0.1)"), i = 1, size(OmegaM))
        do i = 1, size(zplus1)
            call setVolComDiffNormed(VolComDiffNormed, getDisComTransNormed(zplus1(i), OmegaM, OmegaL, 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1(i), OmegaM, OmegaL)))
            write(fileUnit, "(*(g0,:,','))") zplus1(i) - 1., VolComDiffNormed       
        end do
        close(fileUnit)
 
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!Compute the Comoving Volume Element in units of Hubble Volume.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
call setVolComDiffNormed(VolComDiffNormed(1), getDisComTransNormed(zplus1 = 1., reltol = sqrt(epsilon(0.)))**2, sqrt(getHubbleParamNormedSq(zplus1 = 1.)))
VolComDiffNormed(1)
+0.00000000
 
 
call setVolComDiffNormed(VolComDiffNormed(1), getDisComTransNormed(zplus1 = 1.1, reltol = sqrt(epsilon(0.)))**2, sqrt(getHubbleParamNormedSq(zplus1 = 1.1)))
VolComDiffNormed(1)
+0.907804910E-2
 
 
call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6, reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6)))
VolComDiffNormed(1:2)
+0.273632020, +0.371431828
 
 
call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.2, reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.2)))
VolComDiffNormed(1:2)
+0.199308142, +0.205419630
 
 
call setVolComDiffNormed(VolComDiffNormed(1:2), getDisComTransNormed(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.4, omegaK = -0.2, sqrtAbsOmegaK = sqrt(0.2), reltol = 0.0001)**2, sqrt(getHubbleParamNormedSq(zplus1 = [ 2., 3.], omegaM = 0.2, omegaL = 0.6, omegaR = 0.4, omegaK = -0.2)))
VolComDiffNormed(1:2)
+0.135484368, +0.118126549
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
fontsize = 17
 
marker ={ "CK" : "-"
        , "IK" : "."
        , "RK" : "-"
        }
xlab =  { "CK" : "redshift: Z ( real/imaginary components )"
        , "IK" : "redshift: Z ( integer-valued )"
        , "RK" : "redshift: Z ( real-valued )"
        }
legends =   [ "$\Omega_M = 1.0, \Omega_\Lambda = 0.0$"
            , "$\Omega_M = 0.3, \Omega_\Lambda = 0.7$"
            , "$\Omega_M = .05, \Omega_\Lambda = .95$"
            ]
 
for kind in ["IK", "CK", "RK"]:
 
    pattern = "*." + kind + ".txt"
    fileList = glob.glob(pattern)
    if len(fileList) == 1:
 
        df = pd.read_csv(fileList[0], delimiter = ",")
 
        fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
        ax = plt.subplot()
 
        if kind == "CK":
            plt.plot( df.values[:, 0]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "r"
                    )
            plt.plot( df.values[:, 1]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "blue"
                    )
        else:
            plt.plot( df.values[:, 0]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "r"
                    )
            ax.legend   ( legends
                        , fontsize = fontsize
                        )
 
        plt.xticks(fontsize = fontsize - 2)
        plt.yticks(fontsize = fontsize - 2)
        ax.set_xlabel(xlab[kind], fontsize = 17)
        ax.set_ylabel("Comoving Volume Element / Hubble Volume", fontsize = 17)
        plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
        ax.tick_params(axis = "y", which = "minor")
        ax.tick_params(axis = "x", which = "minor")
        ax.set_xscale("log")
        ax.set_yscale("log")
 
        plt.savefig(fileList[0].replace(".txt",".png"))
 
    elif len(fileList) > 1:
 
        sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:

test_pm_cosmology

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, September 1, 2012, 12:00 AM, National Institute for Fusion Studies, The University of Texas Austin

Definition at line 3723 of file pm_cosmology.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_cosmology.F90