pm_cosmology::getHubbleParamNormedSq Interface Reference

Generate and return the square of the dimensionless Hubble Parameter \(E(z)^2 = \big(\frac{H(z)}{H_0}\big)^2\) for the default or the specified cosmological parameters.
More...

Detailed Description

Generate and return the square of the dimensionless Hubble Parameter \(E(z)^2 = \big(\frac{H(z)}{H_0}\big)^2\) for the default or the specified cosmological parameters.

Assuming \((\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)\) represent the normalized densities of Dark Matter, Dark Energy, Radiation Energy, and Curvature in a Universe with negligible neutrino mass such that \(\Omega_M + \Omega_\Lambda + \Omega_R + \Omega_K = 1\), the dimensionless Hubble Parameter at a given cosmological redshift \(z\) is defined as (Peebles, 1993, Principles of Physical Cosmology, pp 310-321),

\begin{equation} \large E(z) = \frac{H(z)}{H_0} = \sqrt{\Omega_R(1+z)^4 + \Omega_M(1+z)^3 + \Omega_K(1+z)^2 + \Omega_\Lambda} ~, \end{equation}

where \(H_0\) is the Hubble Constant.
Note that \(E(Z)\) is the time derivative of the logarithm of the scale factor \(a(t)\) of the Universe.

Parameters

[in]	zplus1	: The input scalar or array of the same rank as other array-like arguments, of type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128) representing the redshift plus one, \(\log(z+1)\), at which the square of the dimensionless Hubble Parameter must be computed.
[in]	omegaM	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized matter density in the universe. (optional, default = OMEGA_M. It must be present if omegaL ( \(\Omega_\Lambda\)) is also present.)
[in]	omegaL	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized Dark Energy density in the universe. (optional, default = OMEGA_L. It must be present if omegaR is also present.)
[in]	omegaR	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized radiation density in the universe. (optional, default = OMEGA_R. It must be present if omegaK is also present.)
[in]	omegaK	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized curvature density of the universe. (optional, default = OMEGA_K)

Returns

hubbleParamNormedSq : The output scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 containing the square of the dimensionless Hubble Parameter at the desired redshift.

Possible calling interfaces ⛓

use pm_cosmology, only: getHubbleParamNormedSq
 
hubbleParamNormedSq = getHubbleParamNormedSq(zplus1)
hubbleParamNormedSq = getHubbleParamNormedSq(zplus1, omegaM, omegaL)
hubbleParamNormedSq = getHubbleParamNormedSq(zplus1, omegaM, omegaL, omegaR)
hubbleParamNormedSq = getHubbleParamNormedSq(zplus1, omegaM, omegaL, omegaR, omegaK)

Warning

The condition omegaM + omegaL + omegaR + omegaK = 1 must hold in all circumstances.
The condition 1 <= zplus1 must hold in all circumstances.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

Remarks

The procedures under discussion are elemental.

The complexity of the output value (instead of simply outputting the Hubble Parameter) is to ensure the highest computational efficiency of this and other dependent algorithms by minimizing the potentially redundant calculations.

Note

Dropping all optional arguments corresponds to the \(\Lambda\)CDM Universe with the latest experimental parameter inferences.

Note that omegaK (i.e., the spatial curvature density of the Universe) is defined as omegaK = 1 - omegaM - omegaL - omegaR.
However, it is requested explicitly in this

Setting omegaM = 1 and omegaL = 0 corresponds to the Einstein–de Sitter model of the universe proposed by Albert Einstein and Willem de Sitter in 1932.

See also

LOG_HUBBLE_CONST
HUBBLE_DISTANCE_MPC
HUBBLE_CONST
OMEGA_M
OMEGA_L
OMEGA_R
OMEGA_K

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK, RKH ! All real kinds are supported.
    use pm_cosmology, only: getHubbleParamNormedSq
    use pm_io, only: display_type
 
    implicit none
 
    type(display_type) :: disp
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = 1.1)")
    call disp%show( getHubbleParamNormedSq(zplus1 = 1.1) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = 1.1d0)")
    call disp%show( getHubbleParamNormedSq(zplus1 = 1.1d0) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = 1.1_RKH)")
    call disp%show( getHubbleParamNormedSq(zplus1 = 1.1_RKH) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4])")
    call disp%show( getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4]) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.7)")
    call disp%show( getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.7) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.5, omegaR = 0.2)")
    call disp%show( getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.5, omegaR = 0.2) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.5, omegaR = 0.1, omegaK = 0.1)")
    call disp%show( getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.5, omegaR = 0.1, omegaK = 0.1) )
    call disp%skip()
 
    ! Visualize the Hubble Parameter.
 
    block
 
        use pm_cosmology, only:  HUBBLE_CONST
        use pm_arraySpace, only: getLogSpace
 
        integer(IK) , parameter :: NP = 1000_IK
        real                    :: zplus1(NP)
        integer(IK)             :: i, fileUnit
 
        open(newunit = fileUnit, file = "getHubbleParamNormedSq.RK.txt")
        zplus1 = getLogSpace(logx1 = log(1.), logx2 = log(10.), count = NP)
        do i = 1_IK, size(zplus1, 1, IK)
            write(fileUnit, "(*(g0,:,', '))") zplus1(i) &
                                            , real(HUBBLE_CONST) * sqrt(getHubbleParamNormedSq(zplus1(i))) &
                                            , real(HUBBLE_CONST) * sqrt(getHubbleParamNormedSq(zplus1(i), 1.0, 0.0)) &
                                            , real(HUBBLE_CONST) * sqrt(getHubbleParamNormedSq(zplus1(i), 0.0, 1.0)) &
                                            , real(HUBBLE_CONST) * sqrt(getHubbleParamNormedSq(zplus1(i), .30, .30, .40)) &
                                            , real(HUBBLE_CONST) * sqrt(getHubbleParamNormedSq(zplus1(i), .25, .25, .25, .25))
        end do
        close(fileUnit)
 
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
getHubbleParamNormedSq(zplus1 = 1.1)
+1.10260999
 
 
getHubbleParamNormedSq(zplus1 = 1.1d0)
+1.1026100000000001
 
 
getHubbleParamNormedSq(zplus1 = 1.1_RKH)
+1.10260999999999999999999999999999999
 
 
getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4])
+1.00000000, +3.17000008, +9.05999947, +20.5300007
 
 
getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.7)
+1.00000000, +3.10000014, +8.80000019, +19.9000015
 
 
getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.5, omegaR = 0.2)
+1.00000000, +6.10000038, +24.8000011, +70.9000015
 
 
getHubbleParamNormedSq(zplus1 = [real :: 1, 2, 3, 4], omegaM = 0.3, omegaL = 0.5, omegaR = 0.1, omegaK = 0.1)
+1.00000000, +4.90000010, +17.6000004, +46.9000015
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
linewidth = 2
fontsize = 17
 
marker ={ "CK" : "-"
        , "IK" : "."
        , "RK" : "-"
        }
xlab =  { "CK" : "redshift: z ( real/imaginary components )"
        , "IK" : "redshift: z ( integer-valued )"
        , "RK" : "redshift: z ( real-valued )"
        }
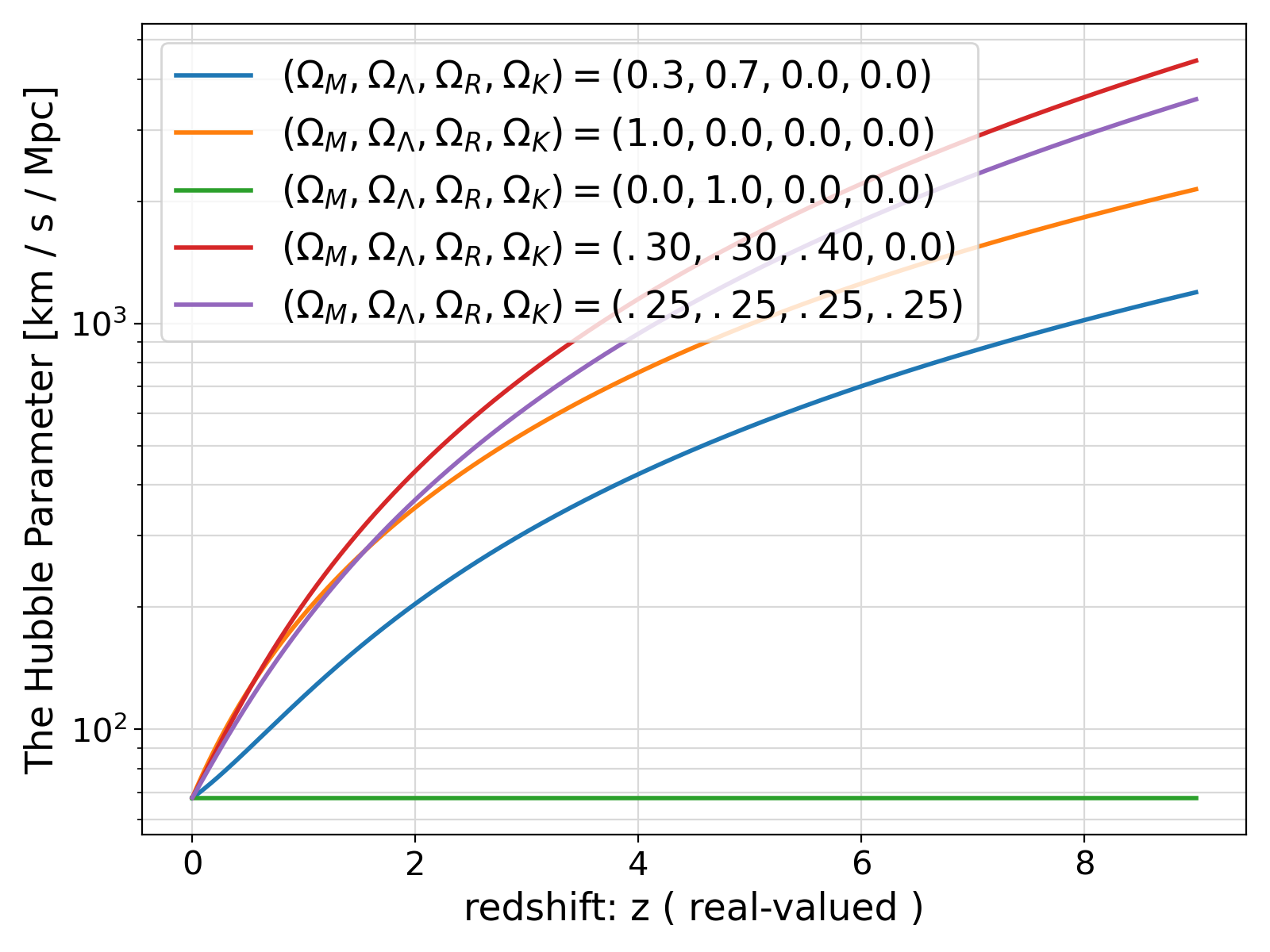
legends =   [ r"$(\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = (0.3, 0.7, 0.0, 0.0)$"
            , r"$(\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = (1.0, 0.0, 0.0, 0.0)$"
            , r"$(\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = (0.0, 1.0, 0.0, 0.0)$"
            , r"$(\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = (.30, .30, .40, 0.0)$"
            , r"$(\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = (.25, .25, .25, .25)$"
            ]
 
for kind in ["IK", "CK", "RK"]:
 
    pattern = "*." + kind + ".txt"
    fileList = glob.glob(pattern)
    if len(fileList) == 1:
 
        df = pd.read_csv(fileList[0], delimiter = ", ")
 
        fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
        ax = plt.subplot()
 
        if kind == "CK":
            plt.plot( df.values[:, 0] - 1
                    , df.values[:,1:6]
                    , marker[kind]
                    , linewidth = linewidth
                   #, color = "r"
                    )
            plt.plot( df.values[:, 1] - 1
                    , df.values[:,1:6]
                    , marker[kind]
                    , linewidth = linewidth
                   #, color = "blue"
                    )
        else:
            plt.plot( df.values[:, 0] - 1
                    , df.values[:,1:6]
                    , marker[kind]
                    , linewidth = linewidth
                   #, color = "r"
                    )
            ax.legend   ( legends
                        , fontsize = fontsize
                        )
 
        plt.xticks(fontsize = fontsize - 2)
        plt.yticks(fontsize = fontsize - 2)
        ax.set_xlabel(xlab[kind], fontsize = 17)
        ax.set_ylabel("The Hubble Parameter [km / s / Mpc]", fontsize = 17)
        #ax.set_xlim([0.0, 5])
        #ax.set_ylim([0.05, 0.5])
        #ax.set_xscale("log")
        ax.set_yscale("log")
 
        plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
        ax.tick_params(axis = "y", which = "minor")
        ax.tick_params(axis = "x", which = "minor")
 
        plt.tight_layout()
        plt.savefig(fileList[0].replace(".txt",".png"))
 
    elif len(fileList) > 1:
 
        sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:

test_pm_cosmology

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, Wednesday 5:43 PM, December 25, 2013, Institute for Fusion Studies, The University of Texas Austin

Definition at line 2963 of file pm_cosmology.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_cosmology.F90