pm_cosmology::getDisComTransNormedWU10 Interface Reference

Generate and return the approximate to the cosmological Transverse Comoving Distance normalized to Hubble Distance, given the user-specified cosmological parameters with negligible Curvature ( \(\Omega_K\)) and Radiation ( \(\Omega_R\)) density parameters. More...

Detailed Description

Generate and return the approximate to the cosmological Transverse Comoving Distance normalized to Hubble Distance, given the user-specified cosmological parameters with negligible Curvature ( \(\Omega_K\)) and Radiation ( \(\Omega_R\)) density parameters.

Assuming \((\Omega_M, \Omega_\Lambda, \Omega_R = 0, \Omega_K = 0)\) represent the normalized densities of Dark Matter, Dark Energy, Radiation Energy, and Curvature in a Universe with negligible neutrino mass such that \(\Omega_M + \Omega_\Lambda + \Omega_R + \Omega_K = 1\), the Transverse Comoving Distance to a given cosmological redshift \(z\) is defined as (e.g., Peebles, 1993),

\begin{equation} \large D_M(z; \Omega_M, \Omega_\Lambda) = \int_{0}^{z} \frac{D_H}{\sqrt{(1+z')^3\Omega_M + \Omega_\Lambda}} ~ dz' ~. \end{equation}

where

1. \(D_M(z; \cdots)\) is the cosmological Transverse Comoving Distance as a function of redshift,
2. \(D_H = \frac{C}{H_0}\) is the Hubble Distance,
3. \(H_0\) is the Hubble Constant.
4. \(C\) is the speed of light,
5. \(z\) is the redshift,

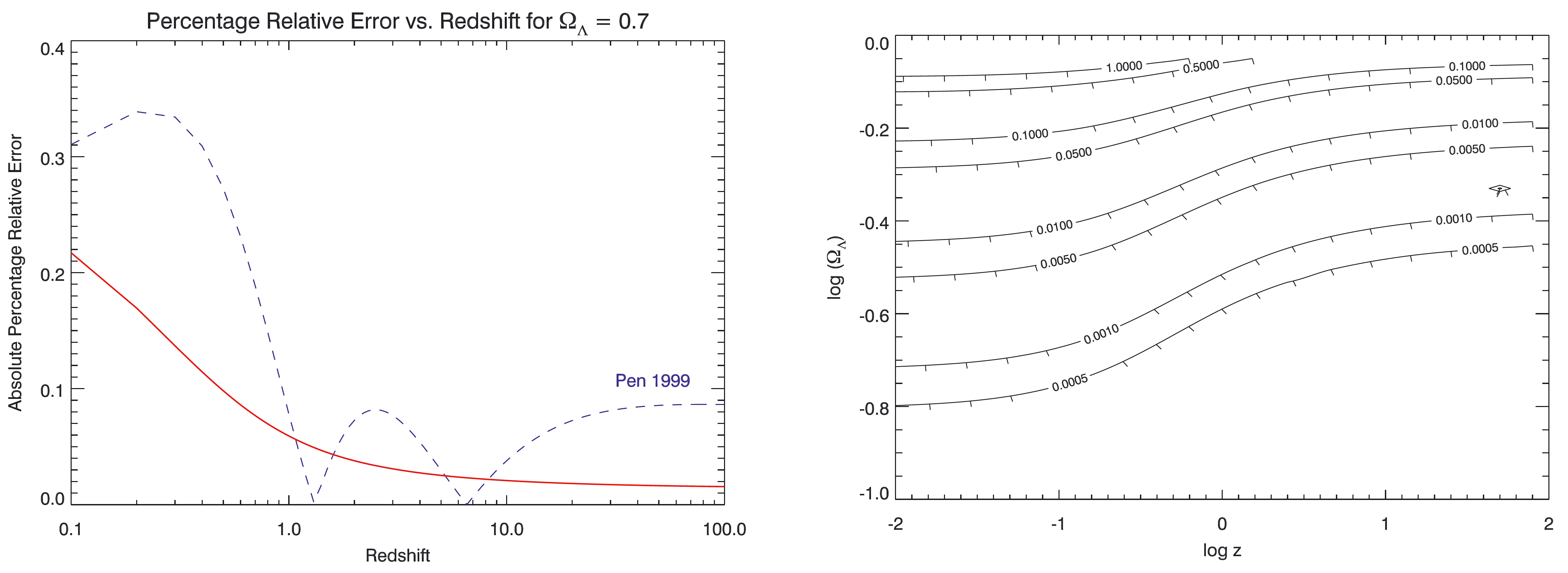
The approximation used in this implementation is based on the work of Wickramasinghe and Ukwatta (2010), WU10.
The method of WU10 claims a relative numerical uncertainty of \(<0.0022\) in the computed Luminosity Distance (hence for the Transverse Comoving Distance) for \((\Omega_M, \Omega_\Lambda) = (0.7, 0.3)\).

Warning

The value returned by the procedures under this generic interface is \(\frac{\tilde{D}_M}{D_H}\), where \(\tilde{D}_M\) is the computed approximation to the true \(D_M\).

Note

To compute the approximate normalized luminosity distance, simply multiply the output of this routine with the factor (z + 1) where z stands for redshift.

Approximation error

The following plots depict the achieved relative percentage errors in the computation of the Transverse Comoving Distance for different values of \(\Omega_\Lambda\) and redshift \(z\).

Warning

Parameters

[in]	zplus1	: The input scalar or array of arbitrary rank of type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128) containing the redshift plus one, \((z+1)\), at which the Transverse Comoving Distance must be computed.
[in]	omegaM	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized matter density in the universe. (optional, default = OMEGA_M. It must be present if omegaL ( \(\Omega_\Lambda\)) is also present.)
[in]	omegaL	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized Dark Energy density in the universe. (optional, default = OMEGA_L. It must be present if omegaM is also present.)

Returns

disComTransNormedWU10 : The output of the same type, kind, and rank as the input argument zplus1 containing the approximate to the Transverse Comoving Distance at the desired redshift normalized to the Hubble Distance.

Possible calling interfaces ⛓

use pm_cosmology, only: getDisComTransNormedWU10
 
disComTransNormedWU10 = getDisComTransNormedWU10(zplus1)
disComTransNormedWU10 = getDisComTransNormedWU10(zplus1, omegaM, omegaL)

Warning

Beware that the actual precision of the output of the procedures under this generic interface is upper bounded by the approximation algorithm at around relative accuracy of 0.002.
This is the case regardless of the real kind and precision requested.

The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

See also

getDisComTransNormed

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK
    use pm_cosmology, only: getDisComTransNormedWU10
    use pm_io, only: display_type
 
    implicit none
 
    type(display_type)      :: disp
 
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!Compute the Transverse Comoving Distance in units of Hubble Distance.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisComTransNormedWU10(zplus1 = 1.)")
    call disp%show( getDisComTransNormedWU10(zplus1 = 1.) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisComTransNormedWU10(zplus1 = 1.1)")
    call disp%show( getDisComTransNormedWU10(zplus1 = 1.1) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisComTransNormedWU10(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6)")
    call disp%show( getDisComTransNormedWU10(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6) )
    call disp%skip()
 
    ! Generate both the cosmic rate and the rate density.
 
    block
 
        use pm_val2str, only: getStr
        use pm_arraySpace, only: getLinSpace
        use pm_arraySpace, only: getLogSpace
 
        real, allocatable   :: zplus1(:), OmegaM(:), OmegaL(:)
        integer :: fileUnit, i
 
        OmegaM = [0.2, 0.3, 0.4]
        OmegaL = 1. - OmegaM
        zplus1 = 1. + getLogSpace(log(0.0001), log(10000.), 500_IK)
 
        open(newunit = fileUnit, file = "getDisComTransNormedWU10.RK.txt")
        write(fileUnit, "(*(g0,:,','))") "z", ("DisLum_"//getStr(OmegaM(i),"(g0.1)")//"_"//getStr(OmegaL(i),"(g0.1)"), i = 1, size(OmegaM))
        do i = 1, size(zplus1)
            write(fileUnit, "(*(g0,:,','))") zplus1(i) - 1., getDisComTransNormedWU10(zplus1(i), OmegaM, OmegaL)
        end do
        close(fileUnit)
 
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

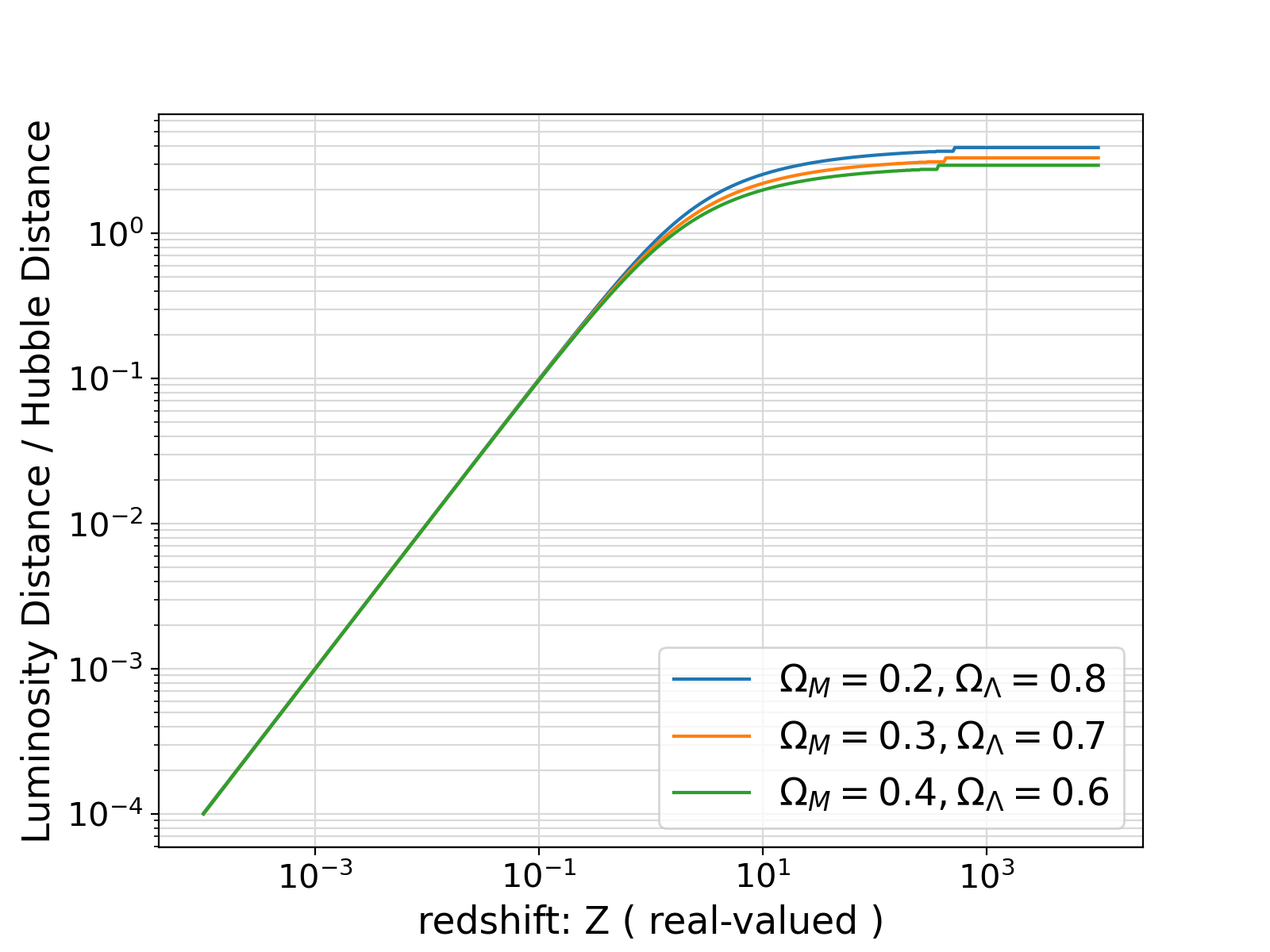
Example output ⛓

 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!Compute the Transverse Comoving Distance in units of Hubble Distance.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
getDisComTransNormedWU10(zplus1 = 1.)
+0.00000000
 
 
getDisComTransNormedWU10(zplus1 = 1.1)
+0.978205502E-1
 
 
getDisComTransNormedWU10(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6)
+0.730501294, +1.12001967
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
fontsize = 17
 
marker ={ "CK" : "-"
        , "IK" : "."
        , "RK" : "-"
        }
xlab =  { "CK" : "redshift: Z ( real/imaginary components )"
        , "IK" : "redshift: Z ( integer-valued )"
        , "RK" : "redshift: Z ( real-valued )"
        }
legends =   [ "$\Omega_M = 0.2, \Omega_\Lambda = 0.8$"
            , "$\Omega_M = 0.3, \Omega_\Lambda = 0.7$"
            , "$\Omega_M = 0.4, \Omega_\Lambda = 0.6$"
            ]
 
for kind in ["IK", "CK", "RK"]:
 
    pattern = "*." + kind + ".txt"
    fileList = glob.glob(pattern)
    if len(fileList) == 1:
 
        df = pd.read_csv(fileList[0], delimiter = ",")
 
        fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
        ax = plt.subplot()
 
        if kind == "CK":
            plt.plot( df.values[:, 0]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "r"
                    )
            plt.plot( df.values[:, 1]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "blue"
                    )
        else:
            plt.plot( df.values[:, 0]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "r"
                    )
            ax.legend   ( legends
                        , fontsize = fontsize
                        )
 
        plt.xticks(fontsize = fontsize - 2)
        plt.yticks(fontsize = fontsize - 2)
        ax.set_xlabel(xlab[kind], fontsize = 17)
        ax.set_ylabel("Luminosity Distance / Hubble Distance", fontsize = 17)
        plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
        ax.tick_params(axis = "y", which = "minor")
        ax.tick_params(axis = "x", which = "minor")
        ax.set_xscale("log")
        ax.set_yscale("log")
 
        plt.savefig(fileList[0].replace(".txt",".png"))
 
    elif len(fileList) > 1:
 
        sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:

test_pm_cosmology

Todo:

High Priority: The origins of the glitch in the output of this algorithm at high redshifts (visible in the plots) must be investigated and corrected.

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, September 1, 2017, 12:00 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 2735 of file pm_cosmology.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_cosmology.F90