|
ParaMonte MATLAB 3.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
|
ParaMonte MATLAB 3.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
Go to the source code of this file.
Functions | |
| function | getLogUDF (in x, in y, in epsilon) |
| Return the natural logarithm of the Unnormalized Density Function (UDF) of the inverse of the 2-dimensional modified Himmelblau function. More... | |
| function getLogUDF | ( | in | x, |
| in | y, | ||
| in | epsilon | ||
| ) |
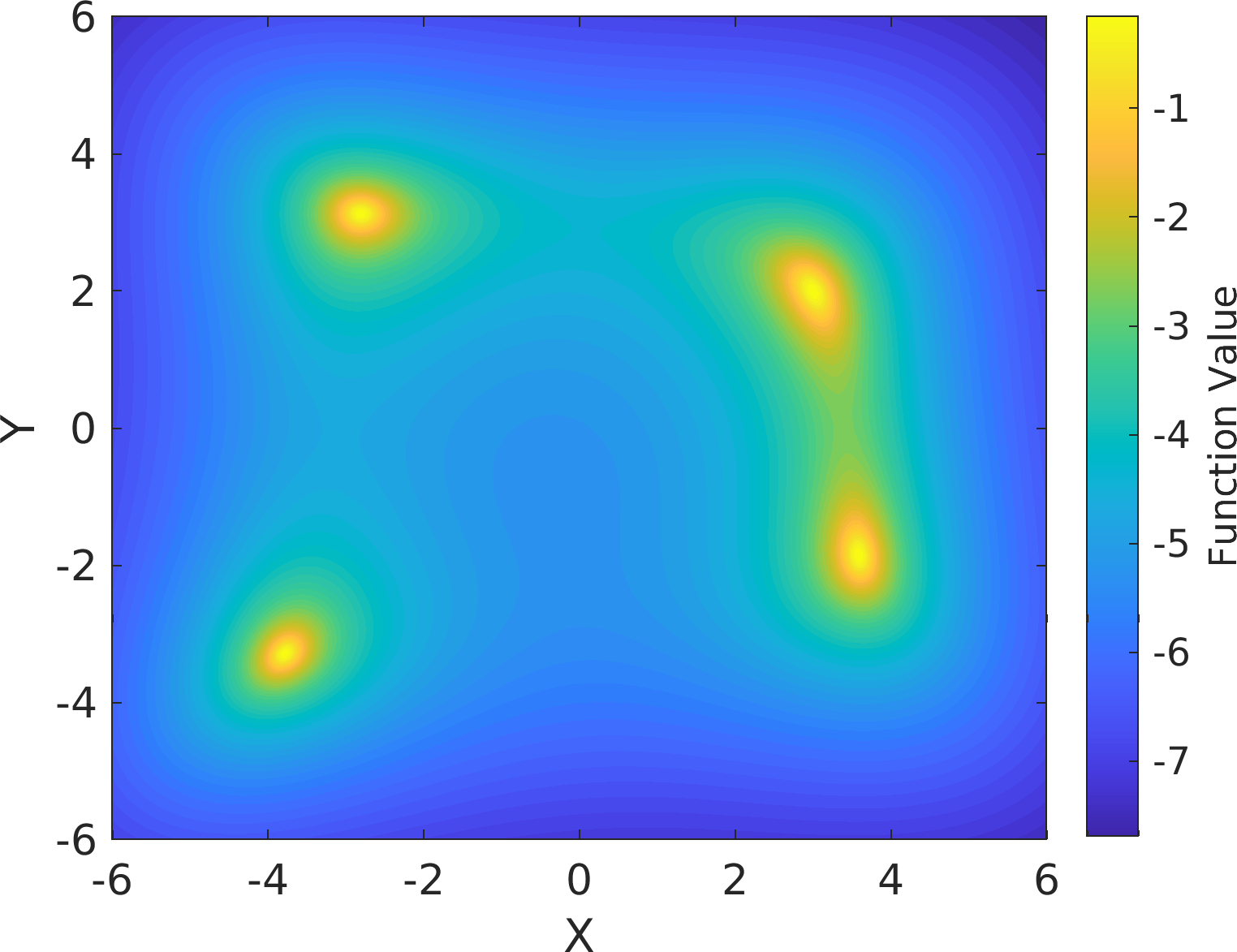
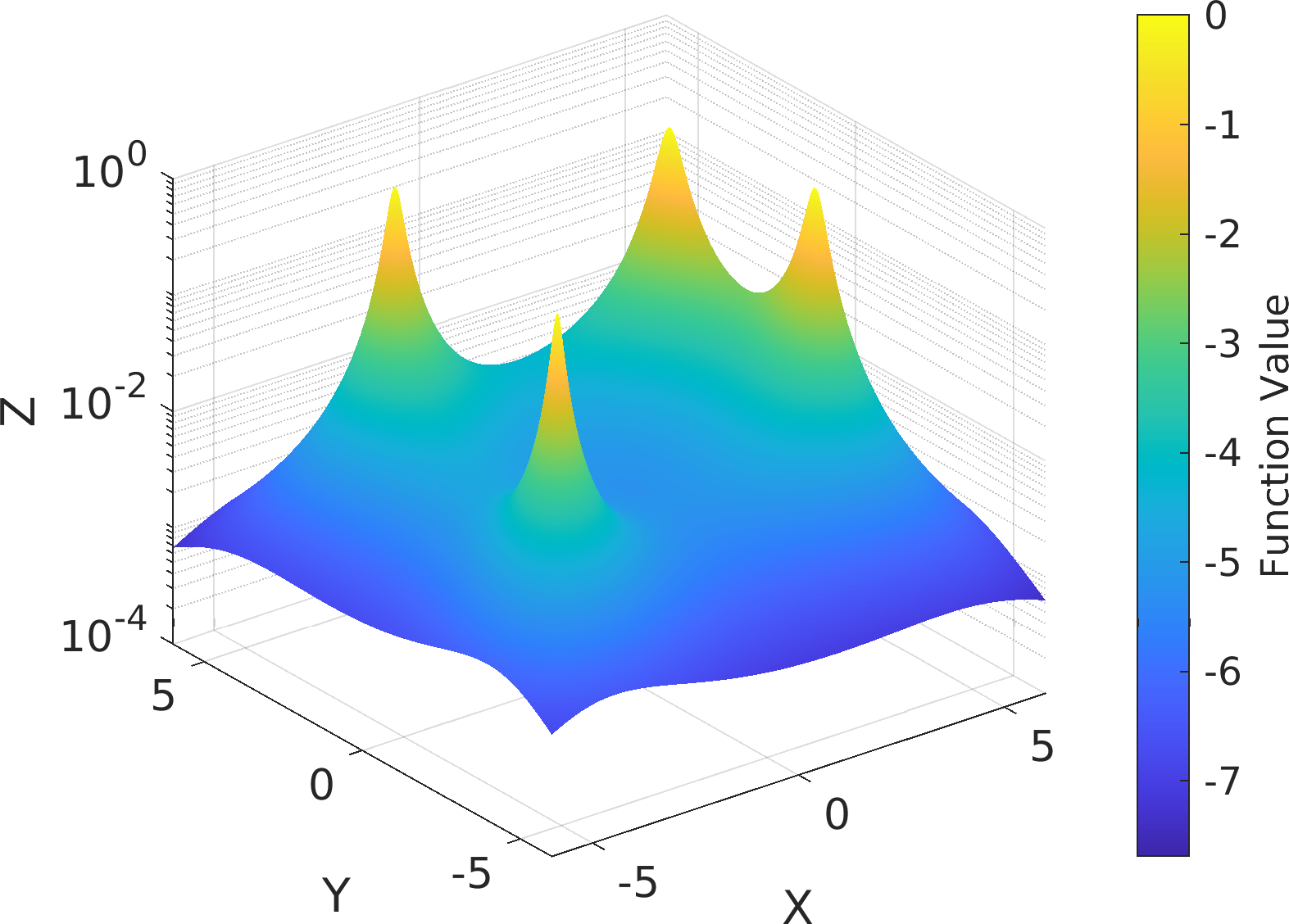
Return the natural logarithm of the Unnormalized Density Function (UDF) of the inverse of the 2-dimensional modified Himmelblau function.
Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:
\begin{equation} H(x, y) = (x^{2} + y - 11)^{2} + (x + y^{2} - 7)^{2} ~. \end{equation}
It has one local maximum at x = -0.270845 and y = -0.923039 where H(x, y) = 181.617, and four identical local minima:
\begin{eqnarray} H(3.0,2.0) &=& 0.0 ~,\\ H(-2.805118, 3.131312) &=& 0.0 ~,\\ H(-3.779310, -3.283186) &=& 0.0 ~,\\ H(3.584428, -1.848126) &=& 0.0 ~. \end{eqnarray}
The function is named after David Mautner Himmelblau (1924–2011), who introduced it.
The locations of all the minima can be found analytically.
This MATLAB function returns a modification of the Himmelblau function as a density function suitable for testing sampling algorithms (or stochastic maximizers):
\begin{equation} f(x, y, \epsilon) = \frac{1}{H(x, y) + \epsilon} ~. \end{equation}
where \epsilon is an arbitrary positive real number which determines the sharpness of the function four peaks.
| [in] | x | : The input scalar or array of the same rank and shape as other input array-like arguments of type MATLAB double, representing the x-component of the state within the domain of Himmelblau density at which the density value must be computed. |
| [in] | y | : The input scalar or array of the same rank and shape as other input array-like arguments of type MATLAB double, representing the y-component of the state within the domain of Himmelblau density at which the density value must be computed. |
| [in] | epsilon | : The input positive scalar or array of the same rank and shape as other array-like input arguments of type MATLAB double, representing the value to be added to the inverse of the Himmelblau function.Increasingly smaller values of epsilon will yield pointier densities.Increasingly larger values of epsilon will yield flatter densities.(optional, default = 1) |
logUDF : The output Unnormalized Density Function (UDF) of the Himmelblau density at the specified input state.
Possible calling interfaces ⛓
Example usage ⛓
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.