pm_matrixMulAdd Module Reference

This module contains procedures and generic interfaces relevant to combined matrix-matrix or matrix-vector multiplication and addition. More...

Data Types
interface	setMatMulAdd
	Return the result of the multiplication of the input matrices/vector matA and matB in the user-specified form. More...

Variables
character(*, SK), parameter	MODULE_NAME = "@pm_matrixMulAdd"

Detailed Description

This module contains procedures and generic interfaces relevant to combined matrix-matrix or matrix-vector multiplication and addition.

The procedures under the generic interface setMatMulAdd of this module return the result of the multiplication of the input matrices matA and matB in one of the following forms,

\begin{align*} & \ms{matC} \leftarrow \alpha \ms{matA}~~ \ms{matB} + \beta \ms{matC} && \ms{matC} \leftarrow \alpha \ms{matA}~~ \ms{matB}^T + \beta \ms{matC} && \ms{matC} \leftarrow \alpha \ms{matA}~~ \ms{matB}^H + \beta \ms{matC} \\ & \ms{matC} \leftarrow \alpha \ms{matA}^T \ms{matB} + \beta \ms{matC} && \ms{matC} \leftarrow \alpha \ms{matA}^T \ms{matB}^T + \beta \ms{matC} && \ms{matC} \leftarrow \alpha \ms{matA}^T \ms{matB}^H + \beta \ms{matC} \\ & \ms{matC} \leftarrow \alpha \ms{matA}^H \ms{matB} + \beta \ms{matC} && \ms{matC} \leftarrow \alpha \ms{matA}^H \ms{matB}^T + \beta \ms{matC} && \ms{matC} \leftarrow \alpha \ms{matA}^H \ms{matB}^H + \beta \ms{matC} \end{align*}

where \(\cdot^T\) represents a Symmetric transpose, \(\cdot^H\) represents a Hermitian transpose, and matA or matB can be also specified as Symmetric/Hermitian upper/lower triangular matrices.

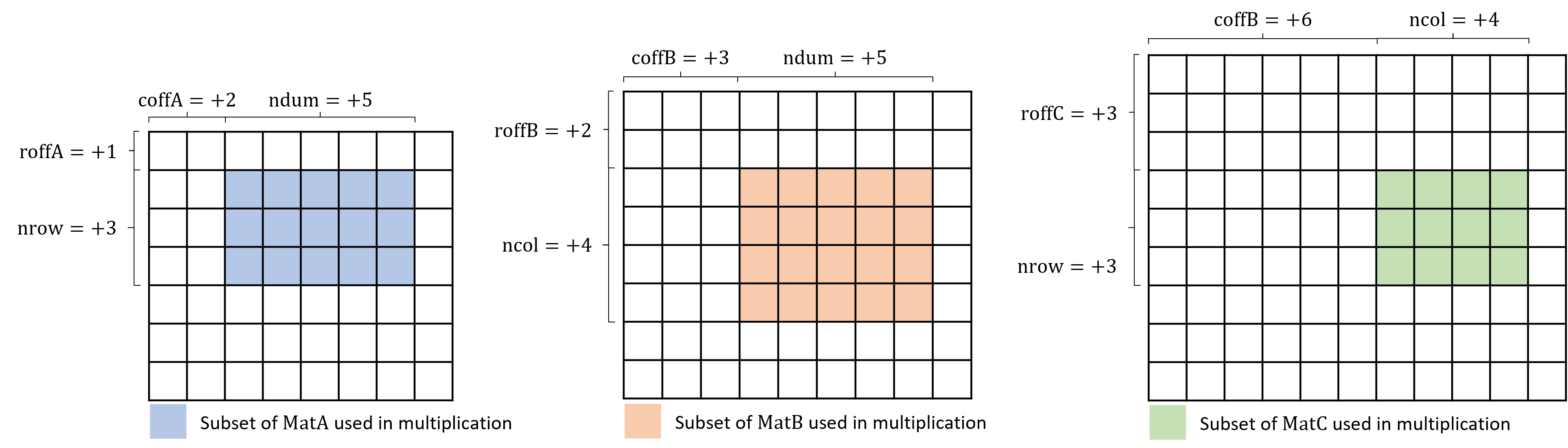
The following figure illustrates the form of the general matrix-matrix or matrix-vector multiplication depending on the input values.

1. Default Multiplication (no transposition involved).
   
   
   
2. Same as the default but with operationA set to transSymm or transHerm.
   
   
   
   
3. Same as the default but with operationB set to transSymm or transHerm.
   
   

For symmetric or Hermitian matrices, only the upper or lower triangles of the corresponding matrices are required and referenced.
Although the implementation is custom-defined for Symmetric/Hermitian matrices, the multiplication is defined as in the figure of case 1 above.

Note

For triangular matrix-matrix or matrix-vector multiplications, see pm_matrixMulTri.

BLAS/LAPACK equivalent:

The procedures under discussion combine, modernize, and extend the interface and functionalities of Version 3.11 of BLAS/LAPACK routine(s): SAXPY, DAXPY, CAXPY, ZAXPY SGEMV, DGEMV, CGEMV, ZGEMV SSPMV, DSPMV, CHPMV, ZHPMV, SSYMV, DSYMV, CHEMV, ZHEMV, SGEMM, DGEMM, CGEMM, ZGEMM, SSYMM, DSYMM, CSYMM, ZSYMM, CHEMM, ZHEMM.
In particular multiplications of matrices of type integer of arbitrary kinds are also possible.

See also

lowDia
uppDia
symmetric
hermitian
transSymm
transHerm
setMatMulTri

Benchmarks:

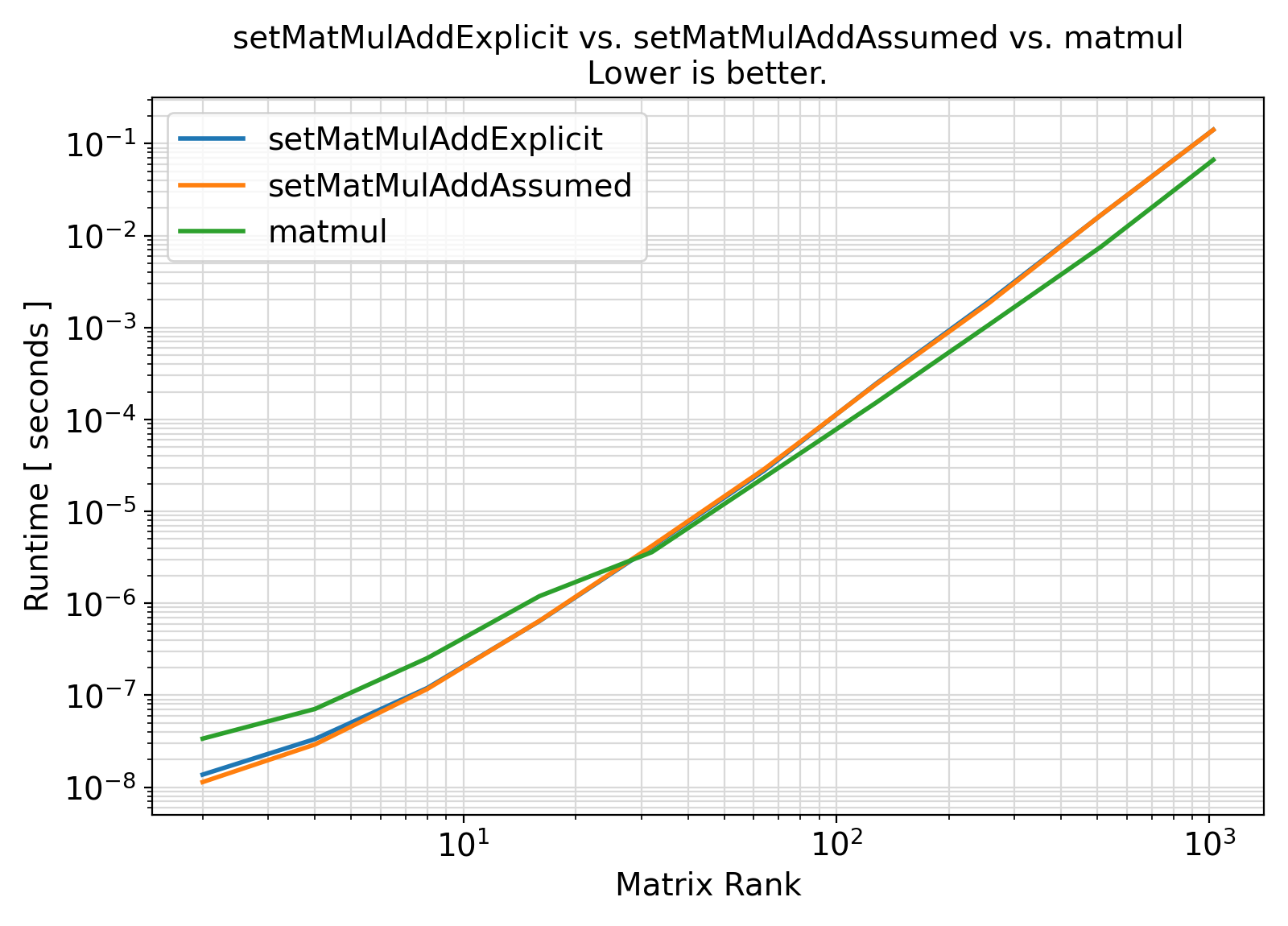
Benchmark :: The runtime performance of setMatMulAdd vs. other other approaches. ⛓

! Test the performance of `setMatMulAdd()` vs. optimized BLAS.
program benchmark
 
    use pm_matrixInit, only: getMatInit, uppLowDia
    use pm_matrixMulAdd, only: setMatMulAdd
    use pm_distUnif, only: setUnifRand
    use iso_fortran_env, only: error_unit
    use pm_kind, only: SK, IK, RKG => RK
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                                 :: itry, ntry
    integer(IK)                                 :: ibench
    integer(IK)                                 :: irank
    integer(IK)                                 :: rank
    integer(IK)                                 :: fileUnit
    integer(IK) , parameter                     :: NUM_RANK = 10_IK
    integer(IK) , parameter                     :: MAX_RANK = 2**NUM_RANK
    integer(IK) , parameter                     :: MAX_ITER = 10000
    real(RKG)   , parameter                     :: ALPHA = 1._RKG
    real(RKG)   , parameter                     :: BETA = 1._RKG
    real(RKG)                                   :: dummySum = 0._RKG
    real(RKG)   , dimension(:,:), allocatable   :: matA, matB, matC
    type(bench_type)            , allocatable   :: bench(:)
 
    bench = [ bench_type(name = SK_"setMatMulAddExplicit", exec = setMatMulAddExplicit, overhead = setOverhead) &
            , bench_type(name = SK_"setMatMulAddAssumed", exec = setMatMulAddAssumed, overhead = setOverhead) &
            , bench_type(name = SK_"matmul", exec = setMatMulTri, overhead = setOverhead) &
#if         BLAS_ENABLED
            , bench_type(name = SK_"GEMM", exec = setBlasGEMM, overhead = setOverhead) &
#endif
            ]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "setMatMulAdd() vs. matmul() vs. GEMM()"
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
        write(fileUnit, "(*(g0,:,', '))") "Matrix Rank", (bench(ibench)%name, ibench = 1, size(bench)) !, (bench(ibench)%name, ibench = 1, size(bench))
        loopOverMatDiaRank: do irank = 1, NUM_RANK
 
            rank = 2**irank
            ntry = MAX_ITER / rank
            write(*,"(*(g0,:,' '))") "Benchmarking with rank:", rank
            matA = getMatInit([rank, rank], uppLowDia, 0._RKG, 0._RKG, 0._RKG); !call setUnifRand(matA)
            matB = getMatInit([rank, rank], uppLowDia, 0._RKG, 0._RKG, 0._RKG); !call setUnifRand(matB)
            matC = getMatInit([rank, rank], uppLowDia, 0._RKG, 0._RKG, 0._RKG); !call setUnifRand(matC)
 
            ! warmup
            call setMatMulAddExplicit()
            call setMatMulAddAssumed()
            call setMatMulTri()
#if         BLAS_ENABLED
            call setBlasGEMM()
#endif
 
            do ibench = 1, size(bench)
                bench(ibench)%timing = bench(ibench)%getTiming(minsec = 0.07_RKG)
            end do
            write(fileUnit, "(*(g0,:,', '))") rank &
                                            , (bench(ibench)%timing%mean / ntry, ibench = 1, size(bench)) !&
                                           !, (bench(1)%timing%mean/bench(ibench)%timing%mean, ibench = 1, NBENCH)
        end do loopOverMatDiaRank
        write(*,"(*(g0,:,' '))") sum(matC)
        write(*,"(*(g0,:,' '))")
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        do itry = 1, ntry
            call getDummy()
        end do
    end subroutine
 
    subroutine getDummy()
        dummySum = dummySum + matC(1,1)
    end subroutine
 
    subroutine setMatMulAddExplicit()
        do itry = 1, ntry
            call setMatMulAdd(matA, matB, matC, alpha, beta, rank, rank, rank, 0_IK, 0_IK, 0_IK, 0_IK, 0_IK, 0_IK)
            call getDummy()
        end do
    end subroutine
 
    subroutine setMatMulAddAssumed()
        do itry = 1, ntry
            call setMatMulAdd(matA, matB, matC)
            call getDummy()
        end do
    end subroutine
 
    subroutine setMatMulTri()
        do itry = 1, ntry
            matC = alpha * matmul(matA(1:rank, 1:rank), matB(1:rank, 1:rank)) + beta * matC(1:rank, 1:rank)
            call getDummy()
        end do
    end subroutine
 
#if BLAS_ENABLED
    subroutine setBlasGEMM()
        do itry = 1, ntry
            call DGEMM( "N" & ! transa
                        , "N" & ! transb
                        , rank & ! m
                        , rank & ! n
                        , rank & ! k
                        , alpha & ! alpha
                        , matA & ! a
                        , rank & ! lda
                        , matB & ! b
                        , rank & ! ldb
                        , beta & ! beta
                        , matC & ! c
                        , rank & ! ldc
                        )
            call getDummy()
        end do
    end subroutine
#endif
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ", ")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

1. The procedures under the generic interface setMatMulAdd are enhancements to the original BLAS routines.
   However, they are currently not optimized for cache-efficient data access on various hardware.
   Similarly, setMatMulAdd does not utilize blocking methods to improve cache access.
   
2. For practical routine daily usages, setMatMulAdd offers a nice generic matrix multiplication interface.
   However, the current implementations are suboptimal to hardware-tuned BLAS libraries such as OpenBLAS and MKL.
   Such performance differences will be most striking for large matrices where cache-efficiency dominates the performance bottleneck.
   

Test:

test_pm_matrixMulAdd

Todo:

Critical Priority: The following BLAS Band-matrix routines must be added to this module:

1. SGBMV, DGBMV, CGBMV, and ZGBMV (Matrix-Vector Product for a General Band Matrix, Its Transpose, or Its Conjugate Transpose).
   
2. SSBMV, DSBMV, CHBMV, and ZHBMV (Matrix-Vector Product for a Real Symmetric or Complex Hermitian Band Matrix).
   
3. STBMV, DTBMV, CTBMV, and ZTBMV (Matrix-Vector Product for a Triangular Band Matrix, Its Transpose, or Its Conjugate Transpose).
   

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, Friday 1:54 AM, April 21, 2017, Institute for Computational Engineering and Sciences (ICES), The University of Texas, Austin, TX

Variable Documentation

MODULE_NAME

character(*, SK), parameter pm_matrixMulAdd::MODULE_NAME = "@pm_matrixMulAdd"

Definition at line 118 of file pm_matrixMulAdd.F90.