
|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |

|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
This module contains classes and procedures for computing the roots of one-dimensional continuous mathematical functions using various root-finding methods.
More...
Data Types | |
| type | bisection_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Bisection method of root-finding. More... | |
| type | bracket_type |
This is an abstract derived type for constructing concrete derived types to distinguish various procedure signatures that require bracketing root-finding methods (e.g., Bisection, False Position, ...).More... | |
| type | brent_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Brent method of root-finding. More... | |
| type | false_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the False-Position method of root-finding. More... | |
| interface | getRoot |
| Generate and return a root of a specified continuous real-valued one-dimensional mathematical function such that f(\mathrm{root}) = 0 with the user-specified or the default root-finding method. More... | |
| type | halley_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Halley method of root-finding. More... | |
| type | hybrid_type |
This is an abstract derived type for constructing concrete derived types to distinguish various procedure signatures that require iterative root-finding methods (e.g., Secant, Newton, ...).More... | |
| type | iteration_type |
This is an abstract derived type for constructing concrete derived types to distinguish various procedure signatures that require iterative root-finding methods (e.g., Secant, Newton, ...).More... | |
| type | method_type |
This is an abstract derived type for constructing concrete derived types to distinguish various procedure signatures that require root-finding methods (e.g., Bisection, False Position, Secant, Newton, Brent, Ridders, ...).More... | |
| type | newton_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Newton method of root-finding. More... | |
| type | ridders_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Ridders method of root-finding. More... | |
| type | schroder_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Schroder method of root-finding. More... | |
| type | secant_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the Secant method of root-finding. More... | |
| interface | setRoot |
| Return a root of a specified continuous real-valued one-dimensional mathematical function such that f(\mathrm{root}) = 0 with the user-specified or the default root-finding method. More... | |
| type | toms748_type |
| This is a concrete derived type whose instances are exclusively used to signify the use of the TOMS748 method of root-finding. More... | |
Variables | |
| character(*, SK), parameter | MODULE_NAME = "@pm_mathRoot" |
| type(brent_type), parameter | brent = brent_type() |
This is a scalar parameter object of type brent_type that is exclusively used to signify the use of Brent method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(toms748_type), parameter | toms748 = toms748_type() |
This is a scalar parameter object of type toms748_type that is exclusively used to signify the use of TOMS748 method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(false_type), parameter | false = false_type() |
This is a scalar parameter object of type false_type that is exclusively used to signify the use of False-Position method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(secant_type), parameter | secant = secant_type() |
This is a scalar parameter object of type secant_type that is exclusively used to signify the use of Secant method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(newton_type), parameter | newton = newton_type() |
This is a scalar parameter object of type newton_type that is exclusively used to signify the use of Newton method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(halley_type), parameter | halley = halley_type() |
This is a scalar parameter object of type halley_type that is exclusively used to signify the use of Halley method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(schroder_type), parameter | schroder = schroder_type() |
This is a scalar parameter object of type schroder_type that is exclusively used to signify the use of Schroder method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(ridders_type), parameter | ridders = ridders_type() |
This is a scalar parameter object of type ridders_type that is exclusively used to signify the use of Ridders method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
| type(bisection_type), parameter | bisection = bisection_type() |
This is a scalar parameter object of type bisection_type that is exclusively used to signify the use of Bisection method of root-finding within an interface of a procedure of the ParaMonte library.More... | |
This module contains classes and procedures for computing the roots of one-dimensional continuous mathematical functions using various root-finding methods.
In mathematics and computing, a root-finding algorithm is an algorithm for finding zeros, also called roots, of continuous functions.
A zero of a function f, from the real numbers to real numbers or from the complex numbers to the complex numbers, is a number x such that f(x) = 0.
As, generally, the zeros of a function cannot be computed exactly nor expressed in closed form, root-finding algorithms provide approximations to zeros expressed either as floating-point numbers or as small isolating intervals, or disks for complex roots.
Solving an equation f(x) = g(x) is the same as finding the roots of the function h(x) = f(x) – g(x).
Thus root-finding algorithms allow solving any equation defined by continuous functions.
However, most root-finding algorithms do not guarantee that they will find all the roots.
If such an algorithm does not find any root, it does not mean that no root exists.
Most numerical root-finding methods use iteration, producing a sequence of numbers that hopefully converges towards the root as its limit.
They require one or more initial guesses of the root as starting values, then each iteration of the algorithm produces a successively more accurate approximation to the root.
Since the iteration must be stopped at some point, these methods produce an approximation to the root, not an exact solution.
Bracketing methods determine successively smaller intervals (brackets) that contain a root.
When the interval is small enough, then a root has been found.
They generally use the intermediate value theorem, which asserts that if a continuous function has values of opposite signs at the end points of an interval, then the function has at least one root in the interval.
Therefore, they require to start with an interval such that the function takes opposite signs at the end points of the interval.
There are other methods for getting information on the number of roots of polynomials in an interval.
The Bisection method consists of repeatedly bisecting a pre-specified interval known to contain at least one root.
The method selects the subinterval in which the function changes sign, and therefore must contain a root.
It is a very simple and robust, but relatively slow root-finding method.
As such, it is frequently used to obtain a rough approximation to the solution of a given root-finding problem.
The approximate solution is then used as a starting point for more rapidly converging methods.
The Bisection Algorithm
The Bisection method numerically solves the real-valued equation f(x) = 0.
The continuous function f is defined on a search interval [a, b] with f(a) and f(b) having opposite signs.
In such a case a and b are said to bracket a root f must have at least one root in the search interval (a, b).
At each step, the method divides the interval in two parts (halves) by computing the midpoint c = (a + b) / 2 of the interval and f(c).
If c is a root then the process has succeeded and stops.
Otherwise, there are now only two possibilities:
If the function has the same sign at the endpoints of an interval, the endpoints may or may not bracket roots of the function.
The Bisection method selects the subinterval that is guaranteed to be a bracket as the new interval to be used in the next step.
In this way an interval that contains a zero of f is reduced in width by half at each step.
The process is continued until the interval is sufficiently small.
The False Position method is a root-finding algorithm is a very old method for solving an equation with one unknown.
In simple terms, the method is the trial and error technique of using test (false) values for the variable and then adjusting the test value according to the outcome.
This is sometimes also referred to as guess and check.
Versions of the method predate the advent of algebra and the use of equations.
The False Position Algorithm
The Regula Falsi method calculates the new solution estimate as the x-intercept of the line segment joining the endpoints of the function on the current bracketing interval of the root.
Essentially, the root is being approximated by replacing the actual function by a line segment on the bracketing interval and then using the classical double false position formula on that line segment.
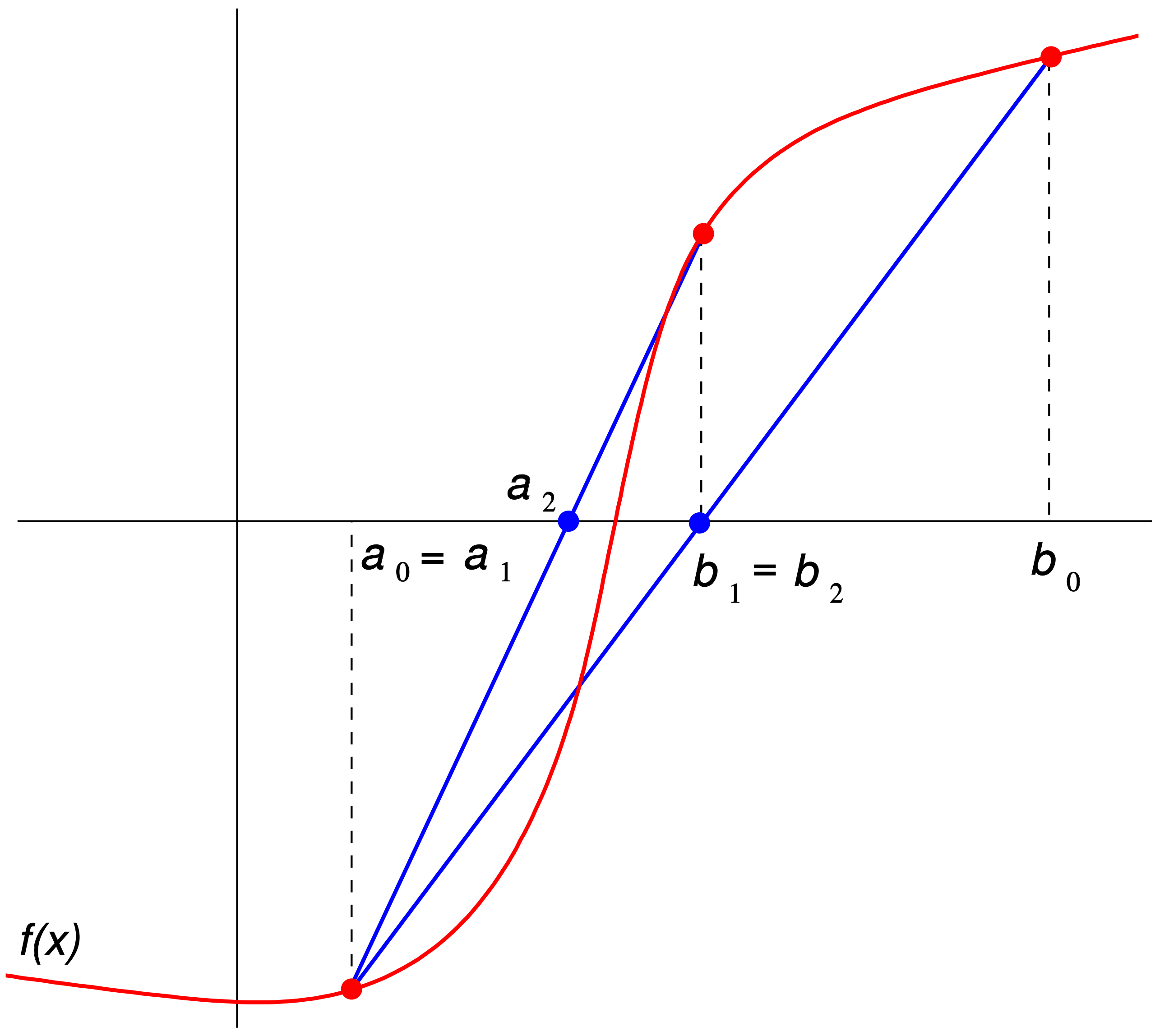
Suppose that in the k-th iteration the bracketing interval is (a_k, b_k) as illustrated above.
Construct the line through the points (a_k, f(a_k)) and (b_k, f(b_k)).
The equation of the line is given by,
\begin{equation} \large y - f(b_k) = \frac{f(b_k) - f(a_k)}{b_k - a_k} (x - b_k) ~. \end{equation}
Now choose c_k to be the x-intercept of this line, that is, the value of x for which y = 0, and substitute these values to obtain,
\begin{equation} \large f(b_k) + \frac{f(b_k) - f(a_k)}{b_k - a_k}(c_k - b_k) = 0 ~. \end{equation}
Solving this equation for c_k yields,
\begin{equation} \large c_k = b_k - f(b_k) \frac{b_k - a_k}{f(b_k) - f(a_k)} = \frac{a_k f(b_k) - b_k f(a_k)}{f(b_k) - f(a_k)} ~. \end{equation}
The last symmetrical form has a computational advantage;
As a solution is approached, a_k and b_k will be very close together and nearly always of the same sign.
Such a subtraction can lose significant digits.
Because f(b_k) and f(a_k) are always of opposite sign, the subtraction in the numerator of the improved formula is effectively an addition (as is the subtraction in the denominator).
At iteration number k, the number c_k is calculated as above and then, if f(a_k) and f(c_k) have the same sign, set a_k + 1 = c_k and b_k + 1 = b_k.
Otherwise set a_k + 1 = a_k and b_k + 1 = c_k.
This process is repeated until the root is approximated sufficiently well.
The above formula is also used in the Secant method.
However, the Secant method always retains the last two computed points.
Therefore, while the Secant method is slightly faster, it does not preserve the root bracketing and may not converge.
The fact that the Regula Falsi root-finding method always converges makes it a good choice when speed is needed.
However, its rate of convergence can drop below that of the bisection method.
The Convergence of the False Position Algorithm
The convergence rate of the False Position method can be better than the Bisection method but is worse than the Secant method.
The method often has a superlinear convergence rate.
However, estimation of the exact order of convergence is difficult (e.g., see Numerical Recipes in Fortran by Press et al. 1992 for a discussion).
The Secant method is a root-finding algorithm that uses a succession of roots of secant lines to better approximate a root of a function.
The Secant method can be thought of as a finite-difference approximation of the Newton method.
However, the Secant method predates the Newton method by over 3000 years.
The Secant Algorithm
The Secant method is defined by the following recursive relation,
\begin{eqnarray} \large x_{n} &=& x_{n-1} - f(x_{n-1}) \frac{x_{n-1} - x_{n-2}} {f(x_{n-1}) - f(x_{n-2})} ~, \\ &=& \frac {x_{n-2} f(x_{n-1}) - x_{n-1} f(x_{n-2})} {f(x_{n-1}) - f(x_{n-2})} ~, \end{eqnarray}
where the two initial values x_0 and x_1 should be chosen close to the desired zero.
Convergence of the Secant Algorithm
The iterates x_n of the Secant method converge to a root of a continuous function if the initial values x_0 and x_1 are sufficiently close to the root.
The order of convergence is the Golden Ratio \phi = 1.618, so that the limiting error in the root is,
\begin{equation} \large \lim_{k\rightarrow+\infty} |\epsilon_{k}| \propto |\epsilon_{k - 1}|^{1.618} ~. \end{equation}
The rate of convergence is therefore faster than the Bisection.
In particular, the convergence is super-linear, but sub-quadratic.
This convergence rate only holds under some technical conditions, namely the function must be twice continuously differentiable and the root in question be simple (i.e., with multiplicity 1).
If the initial values are not close enough to the root, then there is no guarantee that the Secant method converges.
There is no general definition of close enough, but the criterion has to do with how wiggly the function is on the interval [x_0, x_1].
For example, if the function is differentiable on the interval and there is a point where f′(x) = 0 on the interval, then the algorithm may not converge.
For functions that are not sufficiently continuous, the algorithm can therefore not be guaranteed to converge: Local behavior might send it off towards infinity.
The Newton method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a root-finding algorithm which produces successively better approximations to the roots (or zeroes) of a real-valued function.
The Newton Algorithm
The most basic version of the method starts with,
If the function satisfies sufficient assumptions and the initial guess is close, then,
\begin{equation} \large x_{1} = x_{0} - \frac{f(x_{0})}{f'(x_{0})} ~, \end{equation}
is a better approximation of the root than x_0 (as illustrated below).
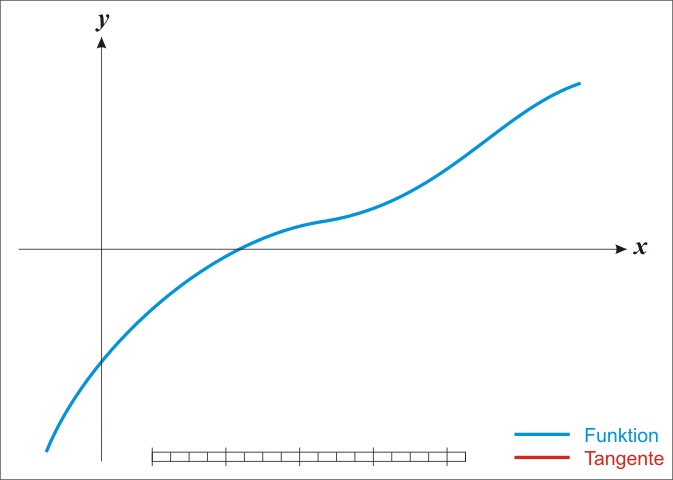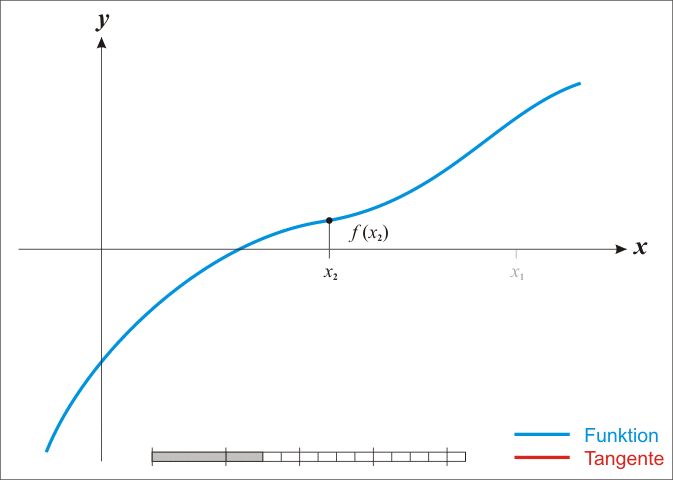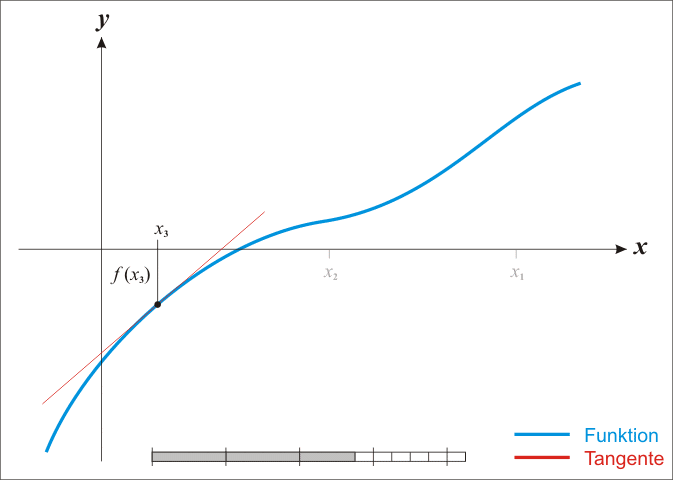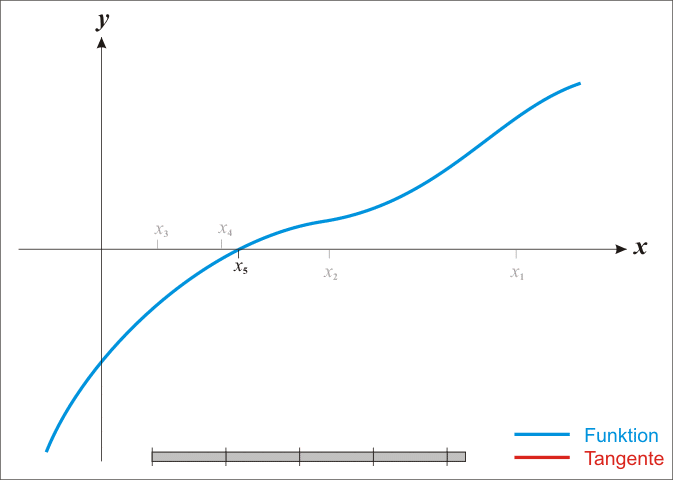
Geometrically, (x_1, 0) is the intersection of the x-axis and the tangent of the graph of f at (x_0, f(x_0)).
In other words, the improved guess is the unique root of the linear approximation at the initial point.
The process is repeated as,
\begin{equation} \large x_{n+1} = x_{n} - \frac {f(x_{n})}{f'(x_{n})} ~, \end{equation}
until a sufficiently precise value is reached.
The Newton method can also be extended to complex functions and to systems of equations.
The Convergence of the Newton Algorithm
The Newton method will usually converge, provided the initial guess is close enough to the unknown root of the function and f\prime(x_0) \neq 0.
Furthermore, for a root of multiplicity 1, the convergence is at least quadratic in a neighborhood of the root.
This intuitively means that the number of correct digits roughly doubles in every step.
More details can be found in the analysis section below.
Practical Considerations for the Newton Algorithm
The Newton method is a powerful technique.
Convergence is generally quadratic.
However, there are some difficulties associated with the method.
\begin{equation} \large f(x) = |x|^{a} ~, \quad 0 < a < \frac{1}{2} ~, \end{equation}
for which the root will be overshot and the sequence of x will diverge.In numerical analysis, the Halley method is a root-finding algorithm used for functions of one real variable with a continuous second derivative.
It is named after its inventor Edmond Halley.
The algorithm is second in the class of Householder methods, after Newton method.
Like the latter, it iteratively produces a sequence of approximations to the root.
The rate of convergence to the root is cubic.
The Halley method exactly finds the roots of a linear-over-linear Padé approximation to the function, in contrast to the Newton method or the Secant method which approximate the function linearly, or the Muller method which approximates the function quadratically.
The Halley Algorithm
The Halley method solves the nonlinear equation f(x) = 0.
In this case, the function f has to be a function of one real variable.
The method consists of a sequence of iterations:
\begin{equation} x_{{n+1}} = x_{n} - \frac{2f(x_{n})f'(x_{n})}{2{[f'(x_{n})]}^{2}-f(x_{n})f''(x_{n})} ~, \end{equation}
beginning with an initial guess x_0.
The Convergence of the Halley Algorithm
The Halley method converges cubically to the function root.
That is, each iteration triples the number of significant digits in the final root.
In comparison, two steps of Newton-Raphson quadruple the number of digits in the final root.
Practical Considerations for the Halley Algorithm
The use of the Halley method is sensible only when it is easy to calculate the second derivative of the target function.
The basin of convergence of the Halley method is not guaranteed to be larger than that of the Newton method.
This means that the Halley method does not necessarily yield faster convergence rates as evidenced by the examples of the generic interfaces of this module.
he current implementation of the Halley method in this module resolves over-compensations by the second derivative (leading to wrong search directions) by reverting the search method to a Newton-Raphson step.
If the method sends the search out of the initial user-specified bracket of the root, then the algorithm falls back to the bisection method to correct the search.
Similar to the Halley method, the Schroder method solves the nonlinear equation f(x) = 0 using the second derivative.
However, unlike the Newton and the Halley methods, the Schroder method is known to work well in the presence of multiple roots.
The method consists of a sequence of iterations:
\begin{equation} x_{{n+1}} = x_{n} - \frac{f(x_n)}{f'(x_n)} - \frac{[f(x_n)]^2 f''(x_n)}{2[f'(x_n)]^3} ~, \end{equation}
beginning with an initial guess x_0.
See Stewart, 1993, G. W. On Infinitely Many Algorithms for Solving Equations for the English translation of the original paper of Schroder and the derivation of the above equation on page 13.
The Brent method is a hybrid root-finding algorithm combining
It has the reliability of the Bisection method but potentially as fast as some of the less-reliable methods above.
The algorithm tries to use the potentially fast-converging Secant method or inverse quadratic interpolation if possible.
If necessary, it falls back to the more robust Bisection method.
The Brent method is due to Richard Brent and builds on an earlier algorithm by Theodorus Dekker.
The Quadratic method employed in the Brent method works well only when the function behaves smoothly.
However, they run the serious risk of giving very bad estimates of the root or causing machine failure by an inappropriate division by a very small number.
The Brent method guards against this problem by maintaining the search brackets on the root and checking where the interpolation would land before carrying out divisions.
When the corrections due to the Quadratic method would not land within the search bounds, or when the bounds are not collapsing rapidly enough, the algorithm takes a bisection step.
Thus, the Brent method combines the sureness of the Bisection method with the speed of a higher-order method when appropriate.
The Ridders method is a root-finding algorithm based on the False-Position method and the use of an exponential function to successively approximate a root of a continuous function.
The method is due to C. Ridders.
The Ridders Algorithm
Given two values of the independent variable, x_0 < \mathrm{root} < x_2, the method begins by evaluating the function at the midpoint x_1 = (x_0 + x_2) / 2.
One then finds the unique exponential function e^{ax} such that the function h(x) = f(x) \exp(ax) satisfies h(x_1) = (h(x_0) + h(x_2)) / 2.
Specifically, the parameter a is determined by,
\begin{equation} \large \exp\big(a(x_1 - x_0)\big) = \frac{f(x_1) - \mathrm{sign}\big(f(x_0)\big){\sqrt{f(x_1)^2 - f(x_0) f(x_2)}}}{f(x_2)} ~. \end{equation}
The False-Position method is then applied to the points (x_0, h(x_0)) and (x_2, h(x_2)), leading to a new value x_3 between x_0 and x_2,
\begin{equation} \large x_3 = x_1 + (x_1 - x_0) \frac{\mathrm{sign}\big(f(x_0)\big) f(x_1)} {\sqrt{f(x_1)^2 - f(x_0) f(x_2)}} ~, \end{equation}
which will be used as one of the two bracketing values in the next step of the iteration.
The other bracketing value is taken to be x_1 if f(x_1) f(x_3) < 0 (well-behaved case), or otherwise whichever of x_0 and x_2 has function value of opposite sign to f(x_3).
The procedure terminates when the desired accuracy is achieved.
The Convergence of the Ridders Algorithm
The Ridders method is simpler than the Muller method or the Brent method but with similar performance.
The algorithm converges quadratically when the function is well-behaved.
This implies that the number of additional significant digits found at each step approximately doubles.
However, since the function has to be evaluated twice per iteration, the overall order of convergence of the method is \sqrt{2}.
The root remains bracketed and the length of the bracketing interval at least halves on each iteration, even the function is not well-behaved.
In all circumstances, the convergence is guaranteed.
The TOMS748 algorithm is a hybrid root-finding algorithm introduced in,
that uses a mixture of cubic, quadratic and linear (secant) interpolation to locate the root of a function.
While there is widespread claims of the superior performance of this algorithm compared to the Brent method, there are counter arguments for such benchmarks.
The best root-finding algorithm depends on the problem being solved:
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
| type(bisection_type), parameter pm_mathRoot::bisection = bisection_type() |
This is a scalar parameter object of type bisection_type that is exclusively used to signify the use of Bisection method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1413 of file pm_mathRoot.F90.
| type(brent_type), parameter pm_mathRoot::brent = brent_type() |
This is a scalar parameter object of type brent_type that is exclusively used to signify the use of Brent method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 709 of file pm_mathRoot.F90.
| type(false_type), parameter pm_mathRoot::false = false_type() |
This is a scalar parameter object of type false_type that is exclusively used to signify the use of False-Position method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 885 of file pm_mathRoot.F90.
| type(halley_type), parameter pm_mathRoot::halley = halley_type() |
This is a scalar parameter object of type halley_type that is exclusively used to signify the use of Halley method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1149 of file pm_mathRoot.F90.
| character(*, SK), parameter pm_mathRoot::MODULE_NAME = "@pm_mathRoot" |
Definition at line 460 of file pm_mathRoot.F90.
| type(newton_type), parameter pm_mathRoot::newton = newton_type() |
This is a scalar parameter object of type newton_type that is exclusively used to signify the use of Newton method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1061 of file pm_mathRoot.F90.
| type(ridders_type), parameter pm_mathRoot::ridders = ridders_type() |
This is a scalar parameter object of type ridders_type that is exclusively used to signify the use of Ridders method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1325 of file pm_mathRoot.F90.
| type(schroder_type), parameter pm_mathRoot::schroder = schroder_type() |
This is a scalar parameter object of type schroder_type that is exclusively used to signify the use of Schroder method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 1237 of file pm_mathRoot.F90.
| type(secant_type), parameter pm_mathRoot::secant = secant_type() |
This is a scalar parameter object of type secant_type that is exclusively used to signify the use of Secant method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 973 of file pm_mathRoot.F90.
| type(toms748_type), parameter pm_mathRoot::toms748 = toms748_type() |
This is a scalar parameter object of type toms748_type that is exclusively used to signify the use of TOMS748 method of root-finding within an interface of a procedure of the ParaMonte library.
See the root-finding section in the documentation of pm_mathRoot for more details about this root-finding method.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 797 of file pm_mathRoot.F90.