ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation.
pm_polynomial::setPolyRoot Interface Reference

Return the roots of a polynomial of arbitrary degree specified by its coefficients coef.
More...

Detailed Description

Return the roots of a polynomial of arbitrary degree specified by its coefficients coef.

See the documentation of pm_polynomial for details of the root-finding method.

Parameters
[in,out]root: The output contiguous vector of type complex of the same kind as the input argument coef and the same size as the degree of the polynomial (i.e., size(coef) - 1), containing the roots of the polynomial determined from the polynomial coefficients coef.
If the specified input method argument is of type sgl_type, the argument root has intent(inout) and the input values will be used to initialize the root searching only if the condition method%reckoned == .true. holds.
[out]count: The output scalar of type integer of default kind IK, containing the total number of roots computed and stored in the output vector slice root(1 : count).
A value of count = size(root) implies a successful computation of all polynomial roots.
A value of count = 0 implies a total failure of the algorithm in finding any roots.
The condition count < size(root) occurs if either,
  • the algorithm fails to converge, or
  • the algorithm fails to identify all roots of the polynomial, or
  • the condition coef(size(coef)) == 0. occurs (i.e., when the coefficient of the highest power of the polynomial is zero), or
  • the condition size(coef) < 2 occurs (i.e., when the input polynomial is a constant).
[in]coef: The input contiguous vector of,
  1. type complex of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128), or
  2. type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128),
containing the coefficients of the polynomial in the order of increasing power.
By definition, the degree of the polynomial is size(coef) - 1.
[in]method: The input scalar constant that can be any of the following:
  1. the scalar constant eigen or a constant object of type eigen_type implying the use of the Eigenvalue root-finding method.
  2. the scalar constant jenkins or a constant object of type jenkins_type implying the use of the Jenkins-Traub root-finding method.
  3. the scalar constant laguerre or a constant object of type laguerre_type implying the use of the Laguerre root-finding method.
  4. the scalar constant sgl or a constant object of type sgl_type implying the use of the Skowron-Gould root-finding method.
    This method is yet to be fully implemented.
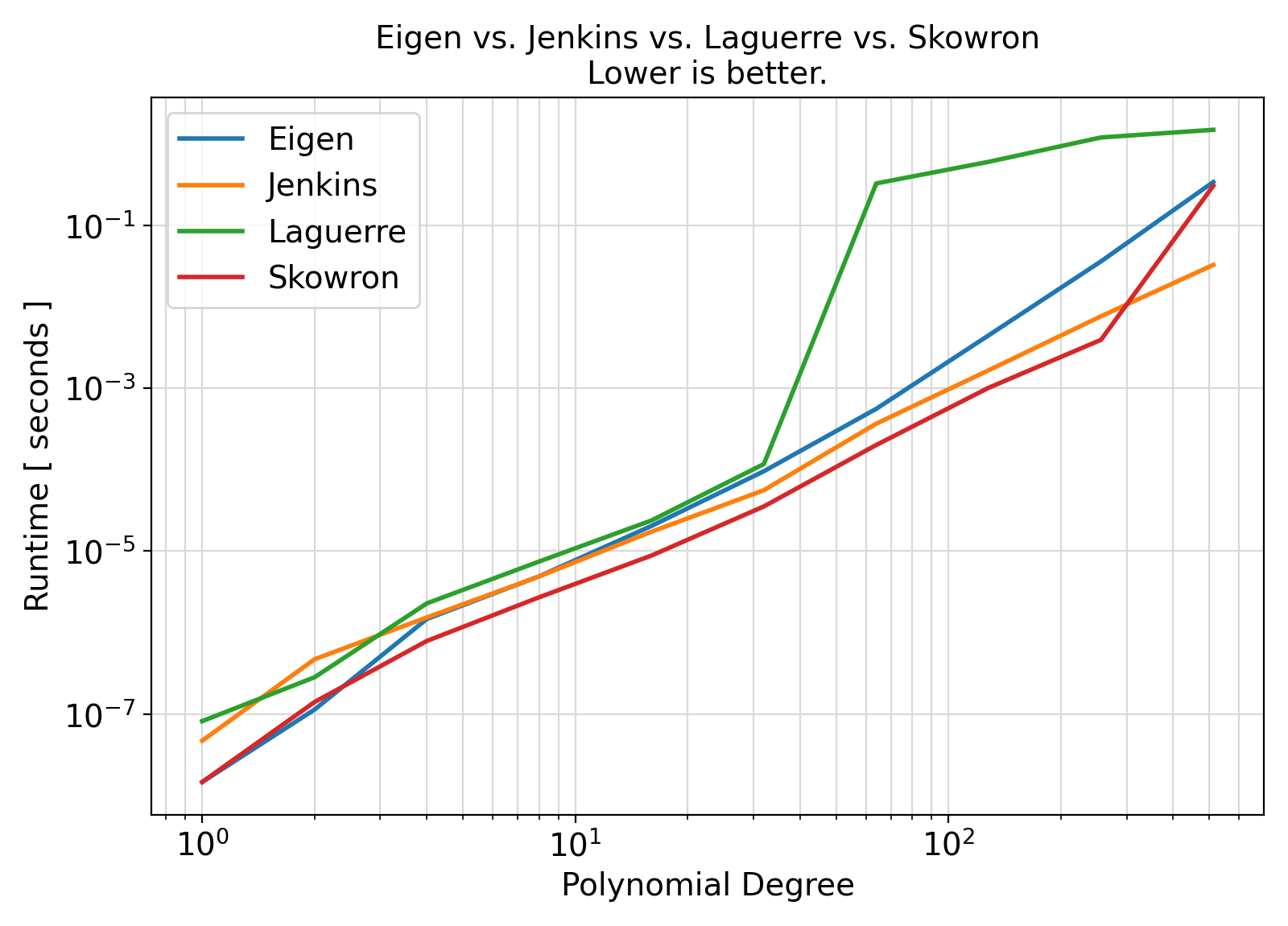
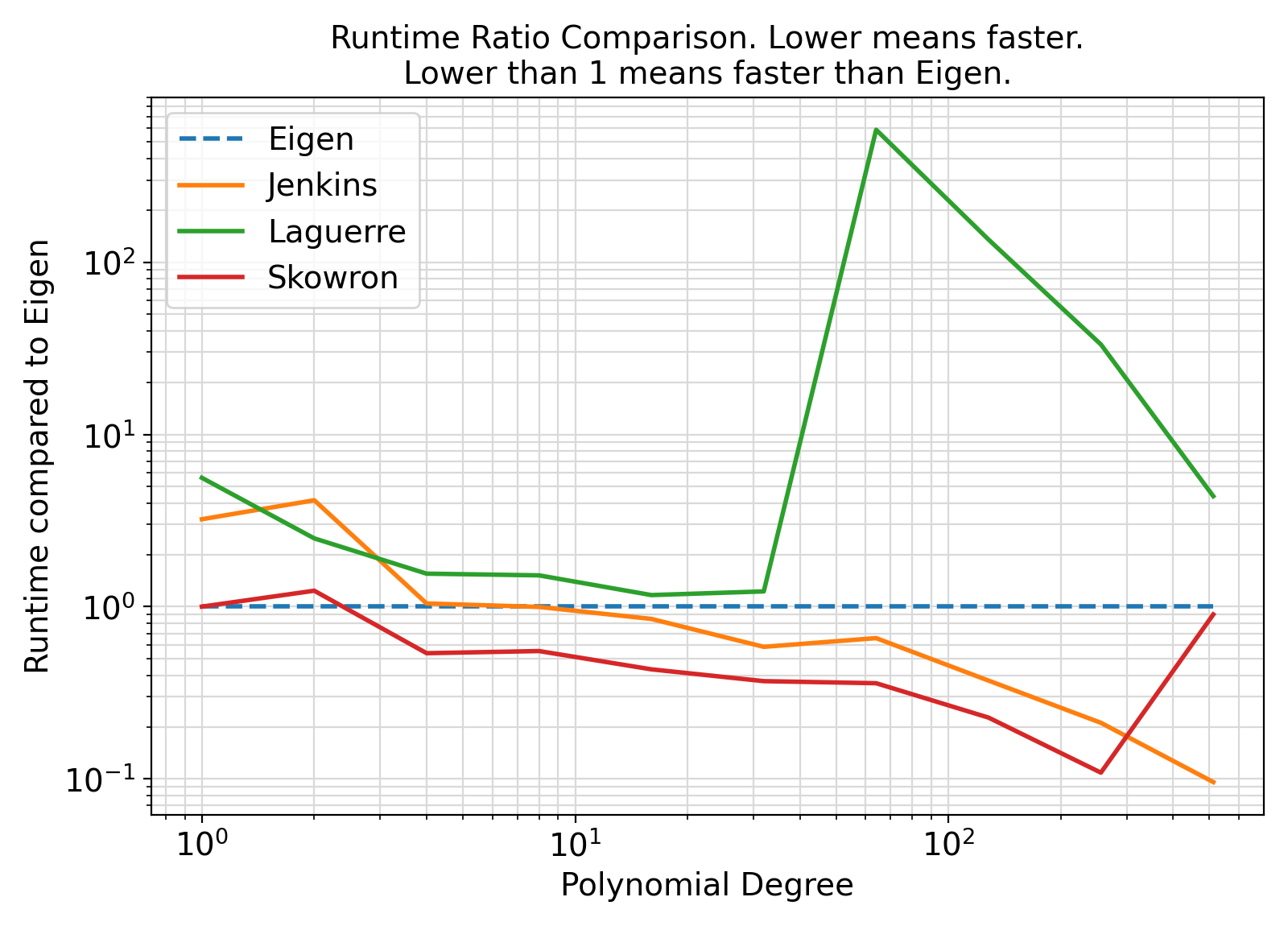
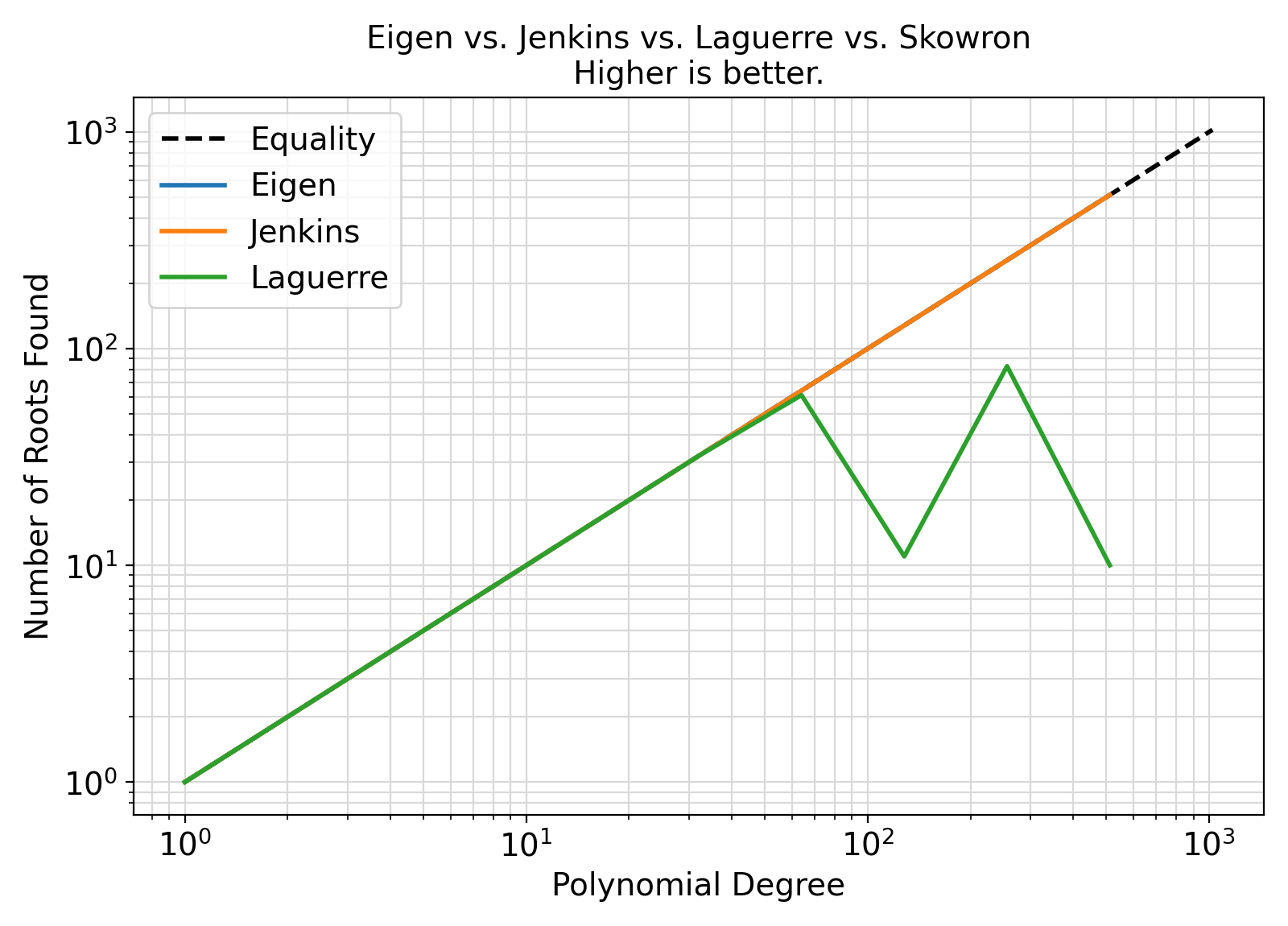
Which polynomial root-finding method should I use?
  1. If you have a polynomial of highly varying coefficients, then the Eigenvalue method as specified by eigen_type is likely more reliable.
  2. The Jenkins-Traub is also considered a relatively reliable fast Sure-Fire technique for finding the roots of polynomials.


Possible calling interfaces ⛓

use pm_polynomial, only: setPolyRoot, eigen_type, jenkins_type, laguerre_type, sgl_type
call setPolyRoot(root(1 : degree), count, coef(0 : degree), method) ! `degree` is the degree of the polynomial.
pm_polynomial::setPolyRoot
Return the roots of a polynomial of arbitrary degree specified by its coefficients coef.
Definition: pm_polynomial.F90:4619
pm_polynomial
This module contains procedures and generic interfaces for performing various mathematical operations...
Definition: pm_polynomial.F90:437
pm_polynomial::eigen_type
This is a concrete derived type whose instances are exclusively used to signify the use of the Eigenv...
Definition: pm_polynomial.F90:3311
pm_polynomial::jenkins_type
This is a concrete derived type whose instances are exclusively used to signify the use of Jenkins-Tr...
Definition: pm_polynomial.F90:3373
pm_polynomial::laguerre_type
This is a concrete derived type whose instances are exclusively used to signify the use of Laguerre m...
Definition: pm_polynomial.F90:3435
pm_polynomial::sgl_type
This is a concrete derived type whose instances are exclusively used to signify the use of Skowron-Go...
Definition: pm_polynomial.F90:3247
Warning
The condition 1 < size(coef) must hold for the corresponding input arguments.
The condition coef(size(coef)) /= 0. must hold for the corresponding input arguments (i.e., the coefficient of the highest-degree term must be non-zero).
The condition all(shape(workspace) == size(coef) - 1) must hold for the corresponding input arguments.
The condition size(root) == size(coef) - 1 must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.
It is crucial to keep in mind that computers use a fixed number of binary digits to represent floating-point numbers.
As such polynomials of high degree can be problematic for root-finding algorithms.
Remarks
The procedures under discussion are impure.
This generic interface combines, significantly extends, and modernizes the SPOLZ, DPOLZ, CPOLZ, and ZPOLZ routines of the MATH77 netlib public-domain library.
See also
getRoot
setRoot
getPolyRoot
setPolyRoot


Example usage ⛓

1program example
2
3 use pm_kind, only: SK, IK, LK
4 use pm_kind, only: RKS, RKD, RKH ! all processor real/complex kinds are supported.
5 use pm_io, only: display_type
6 use pm_polynomial, only: setPolyRoot
7 use pm_polynomial, only: eigen, jenkins, laguerre, sgl
8 use pm_polynomial, only: eigen_type, jenkins_type, laguerre_type, sgl_type
9 use pm_arrayResize, only: setResized
10 use pm_polynomial, only: getPolyVal
11
12 implicit none
13
14 integer(IK) :: count
15
16 type(display_type) :: disp
17 disp = display_type(file = "main.out.F90")
18
19! Template to avoid code duplication in the
20! example for various types and kind parameters.
21! See the output below for the actual code.
22! developer guideline:
23! TYPE - type of coefficient vector: `real`, `complex`
24! RKG - kind of coefficient vector: any supported by the processor
25! CREP - Number of coefficient elements to display per line: use `1` for `real` and `2` for `complex` coefficients.
26#define GET_ROOT(CREP, TYPE, RKG, METHOD) \
27block; \
28use pm_val2str, only: getStr; \
29TYPE(RKG), allocatable :: coef(:); \
30complex(RKG), allocatable :: root(:); \
31type(METHOD) :: method; \
32call disp%skip(); \
33coef = COEF; \
34call disp%show("coef"); \
35call disp%show( coef , format = "(sp,"//getStr(CREP)//"(g0,:,', '))"); \
36call disp%show("call setResized(root, size(coef, 1, IK) - 1_IK)"); \
37 call setResized(root, size(coef, 1, IK) - 1_IK); \
38call disp%show("[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]"); \
39call disp%show( [same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)] ); \
40call disp%show("call setPolyRoot(root, count, coef, eigen)"); \
41 call setPolyRoot(root, count, coef, eigen); \
42call disp%show("count"); \
43call disp%show( count ); \
44call disp%show("root(1:count)"); \
45call disp%show( root(1:count) , format = "(sp,2(g0,:,', '))"); \
46call disp%show("getPolyVal(coef, root(1:count))"); \
47call disp%show( getPolyVal(coef, root(1:count)) , format = "(sp,2(g0,:,', '))"); \
48call disp%skip(); \
49end block;
50
51 call disp%skip()
52 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
53 call disp%show("! Compute the roots of polynomials with real coefficients.")
54 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
55 call disp%skip()
56
57#define COEF \
58 [8, -8, 16, -16, 8, -8]
59 GET_ROOT(1, real, RKS, sgl_type)
60 GET_ROOT(1, real, RKD, sgl_type)
61 GET_ROOT(1, real, RKH, sgl_type)
62 GET_ROOT(1, real, RKS, eigen_type)
63 GET_ROOT(1, real, RKD, eigen_type)
64 GET_ROOT(1, real, RKH, eigen_type)
65 GET_ROOT(1, real, RKS, jenkins_type)
66 GET_ROOT(1, real, RKD, jenkins_type)
67 GET_ROOT(1, real, RKH, jenkins_type)
68 GET_ROOT(1, real, RKS, laguerre_type)
69 GET_ROOT(1, real, RKD, laguerre_type)
70 GET_ROOT(1, real, RKH, laguerre_type)
71
72 call disp%skip()
73 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
74 call disp%show("! Compute the roots of polynomials with real coefficients.")
75 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
76 call disp%skip()
77
78#define COEF \
79 [3628800, -10628640, 12753576, -8409500, 3416930, -902055, 157773, -18150, 1320, -55, 1]
80 GET_ROOT(1, real, RKS, sgl_type)
81 GET_ROOT(1, real, RKD, sgl_type)
82 GET_ROOT(1, real, RKH, sgl_type)
83 GET_ROOT(1, real, RKS, eigen_type)
84 GET_ROOT(1, real, RKD, eigen_type)
85 GET_ROOT(1, real, RKH, eigen_type)
86 GET_ROOT(1, real, RKS, jenkins_type)
87 GET_ROOT(1, real, RKD, jenkins_type)
88 GET_ROOT(1, real, RKH, jenkins_type)
89 GET_ROOT(1, real, RKS, laguerre_type)
90 GET_ROOT(1, real, RKD, laguerre_type)
91 GET_ROOT(1, real, RKH, laguerre_type)
92
93 call disp%skip()
94 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
95 call disp%show("! Compute the roots of polynomials with complex coefficients with zeros 1,2,...,10.")
96 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
97 call disp%skip()
98
99#define COEF \
100 [3628800, -10628640, 12753576, -8409500, 3416930, -902055, 157773, -18150, 1320, -55, 1]
101 GET_ROOT(2, complex, RKS, sgl_type)
102 GET_ROOT(2, complex, RKD, sgl_type)
103 GET_ROOT(2, complex, RKH, sgl_type)
104 GET_ROOT(2, complex, RKS, eigen_type)
105 GET_ROOT(2, complex, RKD, eigen_type)
106 GET_ROOT(2, complex, RKH, eigen_type)
107 GET_ROOT(2, complex, RKS, jenkins_type)
108 GET_ROOT(2, complex, RKD, jenkins_type)
109 GET_ROOT(2, complex, RKH, jenkins_type)
110 GET_ROOT(2, complex, RKS, laguerre_type)
111 GET_ROOT(2, complex, RKD, laguerre_type)
112 GET_ROOT(2, complex, RKH, laguerre_type)
113
114 call disp%skip()
115 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
116 call disp%show("! Compute the roots of polynomials with complex coefficients with zeros on imaginary axis.")
117 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
118 call disp%skip()
119
120#define COEF \
121 [(0._RKH, 1._RKH), (-10001.0001_RKH, 0._RKH), (0._RKH, -10001.0001_RKH), (1._RKH, 0._RKH)]
122 GET_ROOT(2, complex, RKD, sgl_type)
123 GET_ROOT(2, complex, RKH, sgl_type)
124 GET_ROOT(2, complex, RKD, eigen_type)
125 GET_ROOT(2, complex, RKH, eigen_type)
126 GET_ROOT(2, complex, RKD, jenkins_type)
127 GET_ROOT(2, complex, RKH, jenkins_type)
128 GET_ROOT(2, complex, RKD, laguerre_type)
129 GET_ROOT(2, complex, RKH, laguerre_type)
130
131 call disp%skip()
132 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
133 call disp%show("! Compute the roots of polynomials with complex coefficients with zeros at 1+i,1/2*(1+i)....1/(2**-9)*(1+i).")
134 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
135 call disp%skip()
136
137#define COEF \
138[ (0._RKH, 9.094947017729282e-13_RKH) \
139, (-4.652065399568528e-10_RKH, -4.652065399568528e-10_RKH) \
140, (1.584803612786345e-7_RKH, 0._RKH) \
141, (-1.154642632172909e-5_RKH, 1.154642632172909e-5_RKH) \
142, (0._RKH, -7.820779428584501e-4_RKH) \
143, (1.271507365163416e-2_RKH, 1.271507365163416e-2_RKH) \
144, (-.2002119533717632e0_RKH, 0._RKH) \
145, (.7567065954208374e0_RKH, -7.567065954208374e-1_RKH) \
146, (0._RKH, 2.658859252929688e0_RKH) \
147, (-1.998046875_RKH, -1.998046875_RKH) \
148, (1._RKH, 0._RKH) \
149]
150GET_ROOT(2, complex, RKD, sgl_type)
151GET_ROOT(2, complex, RKH, sgl_type)
152GET_ROOT(2, complex, RKD, eigen_type)
153GET_ROOT(2, complex, RKH, eigen_type)
154GET_ROOT(2, complex, RKD, jenkins_type)
155GET_ROOT(2, complex, RKH, jenkins_type)
156GET_ROOT(2, complex, RKD, laguerre_type)
157GET_ROOT(2, complex, RKH, laguerre_type)
158
159 call disp%skip()
160 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
161 call disp%show("! Compute the roots of polynomials with complex coefficients with multiple zeros.")
162 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
163 call disp%skip()
164
165#define COEF \
166[ (288._RKH, 0._RKH) \
167, (-1344._RKH, 504._RKH) \
168, (2204._RKH, -2352._RKH) \
169, (-920._RKH, 4334._RKH) \
170, (-1587._RKH, -3836._RKH) \
171, (2374._RKH, 1394._RKH) \
172, (-1293._RKH, 200._RKH) \
173, (284._RKH, -334._RKH) \
174, (3._RKH, 100._RKH) \
175, (-10._RKH, -10._RKH) \
176, (1._RKH, 0._RKH) \
177]
178GET_ROOT(2, complex, RKS, sgl_type)
179GET_ROOT(2, complex, RKD, sgl_type)
180GET_ROOT(2, complex, RKH, sgl_type)
181GET_ROOT(2, complex, RKS, eigen_type)
182GET_ROOT(2, complex, RKD, eigen_type)
183GET_ROOT(2, complex, RKH, eigen_type)
184GET_ROOT(2, complex, RKS, jenkins_type)
185GET_ROOT(2, complex, RKD, jenkins_type)
186GET_ROOT(2, complex, RKH, jenkins_type)
187GET_ROOT(2, complex, RKS, laguerre_type)
188GET_ROOT(2, complex, RKD, laguerre_type)
189GET_ROOT(2, complex, RKH, laguerre_type)
190
191 call disp%skip()
192 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
193 call disp%show("! Compute the roots of polynomials with complex coefficients with 12 zeros evenly distribute on a circle of radius 1. centered at 0+2i.")
194 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
195 call disp%skip()
196
197#define COEF \
198[ (4095._RKH, 0._RKH) \
199, (0._RKH, 24576._RKH) \
200, (-67584._RKH, 0._RKH) \
201, (0._RKH, -112640._RKH) \
202, (126720._RKH, 0._RKH) \
203, (0._RKH, 101376._RKH) \
204, (-59136._RKH, 0._RKH) \
205, (0._RKH, -25344._RKH) \
206, (7920._RKH, 0._RKH) \
207, (0._RKH, 1760._RKH) \
208, (-264._RKH, 0._RKH) \
209, (0._RKH, -24._RKH) \
210, (1._RKH, 0._RKH) \
211]
212GET_ROOT(2, complex, RKS, sgl_type)
213GET_ROOT(2, complex, RKD, sgl_type)
214GET_ROOT(2, complex, RKH, sgl_type)
215GET_ROOT(2, complex, RKS, eigen_type)
216GET_ROOT(2, complex, RKD, eigen_type)
217GET_ROOT(2, complex, RKH, eigen_type)
218GET_ROOT(2, complex, RKS, jenkins_type)
219GET_ROOT(2, complex, RKD, jenkins_type)
220GET_ROOT(2, complex, RKH, jenkins_type)
221GET_ROOT(2, complex, RKS, laguerre_type)
222GET_ROOT(2, complex, RKD, laguerre_type)
223GET_ROOT(2, complex, RKH, laguerre_type)
224
225end program example
pm_arrayResize::setResized
Allocate or resize (shrink or expand) an input allocatable scalar string or array of rank 1....
Definition: pm_arrayResize.F90:249
pm_io::show
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11726
pm_io::skip
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11508
pm_polynomial::getPolyVal
Generate and return the value of the polynomial of arbitrary degree whose coefficients are specified ...
Definition: pm_polynomial.F90:517
pm_val2str::getStr
Generate and return the conversion of the input value to an output Fortran string,...
Definition: pm_val2str.F90:167
pm_arrayResize
This module contains procedures and generic interfaces for resizing allocatable arrays of various typ...
Definition: pm_arrayResize.F90:81
pm_io
This module contains classes and procedures for input/output (IO) or generic display operations on st...
Definition: pm_io.F90:252
pm_io::disp
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
Definition: pm_io.F90:11393
pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268
pm_kind::LK
integer, parameter LK
The default logical kind in the ParaMonte library: kind(.true.) in Fortran, kind(....
Definition: pm_kind.F90:541
pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540
pm_kind::RKD
integer, parameter RKD
The double precision real kind in Fortran mode. On most platforms, this is an 64-bit real kind.
Definition: pm_kind.F90:568
pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539
pm_kind::RKH
integer, parameter RKH
The scalar integer constant of intrinsic default kind, representing the highest-precision real kind t...
Definition: pm_kind.F90:858
pm_kind::RKS
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Definition: pm_kind.F90:567
pm_polynomial::eigen
type(eigen_type), parameter eigen
This is a scalar parameter object of type eigen_type that is exclusively used to signify the use of E...
Definition: pm_polynomial.F90:3337
pm_polynomial::jenkins
type(jenkins_type), parameter jenkins
This is a scalar parameter object of type jenkins_type that is exclusively used to signify the use of...
Definition: pm_polynomial.F90:3399
pm_polynomial::laguerre
type(laguerre_type), parameter laguerre
This is a scalar parameter object of type laguerre_type that is exclusively used to signify the use o...
Definition: pm_polynomial.F90:3461
pm_polynomial::sgl
type(sgl_type), parameter sgl
This is a scalar parameter object of type sgl_type that is exclusively used to signify the use of Sko...
Definition: pm_polynomial.F90:3275
pm_val2str
This module contains the generic procedures for converting values of different types and kinds to For...
Definition: pm_val2str.F90:58
pm_io::display_type
Generate and return an object of type display_type.
Definition: pm_io.F90:10282

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Example output ⛓
1
2!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
3! Compute the roots of polynomials with real coefficients.
4!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
5
6
7coef
8+8.00000000,
9-8.00000000,
10+16.0000000,
11-16.0000000,
12+8.00000000,
13-8.00000000
14call setResized(root, size(coef, 1, IK) - 1_IK)
15[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
16T, F, F, F
17call setPolyRoot(root, count, coef, eigen)
18count
19+5
20root(1:count)
21+0.999999642, +0.00000000,
22-0.429153442E-4, +1.00021696,
23-0.429153442E-4, -1.00021696,
24+0.427067280E-4, +0.999782741,
25+0.427067280E-4, -0.999782741
26getPolyVal(coef, root(1:count))
27+0.114440918E-4, +0.00000000,
28+0.238418579E-5, -0.804837327E-6,
29+0.238418579E-5, +0.804837327E-6,
30+0.190734863E-5, -0.566709787E-6,
31+0.190734863E-5, +0.566709787E-6
32
33
34coef
35+8.0000000000000000,
36-8.0000000000000000,
37+16.000000000000000,
38-16.000000000000000,
39+8.0000000000000000,
40-8.0000000000000000
41call setResized(root, size(coef, 1, IK) - 1_IK)
42[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
43T, F, F, F
44call setPolyRoot(root, count, coef, eigen)
45count
46+5
47root(1:count)
48+0.99999999999999922, +0.0000000000000000,
49+0.95202123961968255E-9, +1.0000000121923602,
50+0.95202123961968255E-9, -1.0000000121923602,
51-0.95202196126464855E-9, +0.99999998780764010,
52-0.95202196126464855E-9, -0.99999998780764010
53getPolyVal(coef, root(1:count))
54+0.23980817331903381E-13, +0.0000000000000000,
55+0.26645352591003757E-14, -0.55147887586065774E-14,
56+0.26645352591003757E-14, +0.55147887586065774E-14,
57+0.35527136788005009E-14, -0.50706995570283210E-14,
58+0.35527136788005009E-14, +0.50706995570283210E-14
59
60
61coef
62+8.00000000000000000000000000000000000,
63-8.00000000000000000000000000000000000,
64+16.0000000000000000000000000000000000,
65-16.0000000000000000000000000000000000,
66+8.00000000000000000000000000000000000,
67-8.00000000000000000000000000000000000
68call setResized(root, size(coef, 1, IK) - 1_IK)
69[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
70T, F, F, F
71call setPolyRoot(root, count, coef, eigen)
72count
73+5
74root(1:count)
75+1.00000000000000000000000000000000019, +0.00000000000000000000000000000000000,
76-0.108472542273474050653982053325797972E-16, +1.00000000000000000335355606599927526,
77-0.108472542273474050653982053325797972E-16, -1.00000000000000000335355606599927526,
78+0.108472542273474053061394483809842788E-16, +0.999999999999999996646443934000722236,
79+0.108472542273474053061394483809842788E-16, -0.999999999999999996646443934000722236
80getPolyVal(coef, root(1:count))
81-0.770371977754894341222391177033970927E-32, +0.00000000000000000000000000000000000,
82-0.308148791101957736488956470813588371E-32, +0.635981983657862231619686642857405375E-32,
83-0.308148791101957736488956470813588371E-32, -0.635981983657862231619686642857405375E-32,
84-0.308148791101957736488956470813588371E-32, +0.597463384770117558391908329517715426E-32,
85-0.308148791101957736488956470813588371E-32, -0.597463384770117558391908329517715426E-32
86
87
88coef
89+8.00000000,
90-8.00000000,
91+16.0000000,
92-16.0000000,
93+8.00000000,
94-8.00000000
95call setResized(root, size(coef, 1, IK) - 1_IK)
96[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
97F, T, F, F
98call setPolyRoot(root, count, coef, eigen)
99count
100+5
101root(1:count)
102+0.999999642, +0.00000000,
103-0.429153442E-4, +1.00021696,
104-0.429153442E-4, -1.00021696,
105+0.427067280E-4, +0.999782741,
106+0.427067280E-4, -0.999782741
107getPolyVal(coef, root(1:count))
108+0.114440918E-4, +0.00000000,
109+0.238418579E-5, -0.804837327E-6,
110+0.238418579E-5, +0.804837327E-6,
111+0.190734863E-5, -0.566709787E-6,
112+0.190734863E-5, +0.566709787E-6
113
114
115coef
116+8.0000000000000000,
117-8.0000000000000000,
118+16.000000000000000,
119-16.000000000000000,
120+8.0000000000000000,
121-8.0000000000000000
122call setResized(root, size(coef, 1, IK) - 1_IK)
123[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
124F, T, F, F
125call setPolyRoot(root, count, coef, eigen)
126count
127+5
128root(1:count)
129+0.99999999999999922, +0.0000000000000000,
130+0.95202123961968255E-9, +1.0000000121923602,
131+0.95202123961968255E-9, -1.0000000121923602,
132-0.95202196126464855E-9, +0.99999998780764010,
133-0.95202196126464855E-9, -0.99999998780764010
134getPolyVal(coef, root(1:count))
135+0.23980817331903381E-13, +0.0000000000000000,
136+0.26645352591003757E-14, -0.55147887586065774E-14,
137+0.26645352591003757E-14, +0.55147887586065774E-14,
138+0.35527136788005009E-14, -0.50706995570283210E-14,
139+0.35527136788005009E-14, +0.50706995570283210E-14
140
141
142coef
143+8.00000000000000000000000000000000000,
144-8.00000000000000000000000000000000000,
145+16.0000000000000000000000000000000000,
146-16.0000000000000000000000000000000000,
147+8.00000000000000000000000000000000000,
148-8.00000000000000000000000000000000000
149call setResized(root, size(coef, 1, IK) - 1_IK)
150[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
151F, T, F, F
152call setPolyRoot(root, count, coef, eigen)
153count
154+5
155root(1:count)
156+1.00000000000000000000000000000000019, +0.00000000000000000000000000000000000,
157-0.108472542273474050653982053325797972E-16, +1.00000000000000000335355606599927526,
158-0.108472542273474050653982053325797972E-16, -1.00000000000000000335355606599927526,
159+0.108472542273474053061394483809842788E-16, +0.999999999999999996646443934000722236,
160+0.108472542273474053061394483809842788E-16, -0.999999999999999996646443934000722236
161getPolyVal(coef, root(1:count))
162-0.770371977754894341222391177033970927E-32, +0.00000000000000000000000000000000000,
163-0.308148791101957736488956470813588371E-32, +0.635981983657862231619686642857405375E-32,
164-0.308148791101957736488956470813588371E-32, -0.635981983657862231619686642857405375E-32,
165-0.308148791101957736488956470813588371E-32, +0.597463384770117558391908329517715426E-32,
166-0.308148791101957736488956470813588371E-32, -0.597463384770117558391908329517715426E-32
167
168
169coef
170+8.00000000,
171-8.00000000,
172+16.0000000,
173-16.0000000,
174+8.00000000,
175-8.00000000
176call setResized(root, size(coef, 1, IK) - 1_IK)
177[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
178F, F, T, F
179call setPolyRoot(root, count, coef, eigen)
180count
181+5
182root(1:count)
183+0.999999642, +0.00000000,
184-0.429153442E-4, +1.00021696,
185-0.429153442E-4, -1.00021696,
186+0.427067280E-4, +0.999782741,
187+0.427067280E-4, -0.999782741
188getPolyVal(coef, root(1:count))
189+0.114440918E-4, +0.00000000,
190+0.238418579E-5, -0.804837327E-6,
191+0.238418579E-5, +0.804837327E-6,
192+0.190734863E-5, -0.566709787E-6,
193+0.190734863E-5, +0.566709787E-6
194
195
196coef
197+8.0000000000000000,
198-8.0000000000000000,
199+16.000000000000000,
200-16.000000000000000,
201+8.0000000000000000,
202-8.0000000000000000
203call setResized(root, size(coef, 1, IK) - 1_IK)
204[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
205F, F, T, F
206call setPolyRoot(root, count, coef, eigen)
207count
208+5
209root(1:count)
210+0.99999999999999922, +0.0000000000000000,
211+0.95202123961968255E-9, +1.0000000121923602,
212+0.95202123961968255E-9, -1.0000000121923602,
213-0.95202196126464855E-9, +0.99999998780764010,
214-0.95202196126464855E-9, -0.99999998780764010
215getPolyVal(coef, root(1:count))
216+0.23980817331903381E-13, +0.0000000000000000,
217+0.26645352591003757E-14, -0.55147887586065774E-14,
218+0.26645352591003757E-14, +0.55147887586065774E-14,
219+0.35527136788005009E-14, -0.50706995570283210E-14,
220+0.35527136788005009E-14, +0.50706995570283210E-14
221
222
223coef
224+8.00000000000000000000000000000000000,
225-8.00000000000000000000000000000000000,
226+16.0000000000000000000000000000000000,
227-16.0000000000000000000000000000000000,
228+8.00000000000000000000000000000000000,
229-8.00000000000000000000000000000000000
230call setResized(root, size(coef, 1, IK) - 1_IK)
231[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
232F, F, T, F
233call setPolyRoot(root, count, coef, eigen)
234count
235+5
236root(1:count)
237+1.00000000000000000000000000000000019, +0.00000000000000000000000000000000000,
238-0.108472542273474050653982053325797972E-16, +1.00000000000000000335355606599927526,
239-0.108472542273474050653982053325797972E-16, -1.00000000000000000335355606599927526,
240+0.108472542273474053061394483809842788E-16, +0.999999999999999996646443934000722236,
241+0.108472542273474053061394483809842788E-16, -0.999999999999999996646443934000722236
242getPolyVal(coef, root(1:count))
243-0.770371977754894341222391177033970927E-32, +0.00000000000000000000000000000000000,
244-0.308148791101957736488956470813588371E-32, +0.635981983657862231619686642857405375E-32,
245-0.308148791101957736488956470813588371E-32, -0.635981983657862231619686642857405375E-32,
246-0.308148791101957736488956470813588371E-32, +0.597463384770117558391908329517715426E-32,
247-0.308148791101957736488956470813588371E-32, -0.597463384770117558391908329517715426E-32
248
249
250coef
251+8.00000000,
252-8.00000000,
253+16.0000000,
254-16.0000000,
255+8.00000000,
256-8.00000000
257call setResized(root, size(coef, 1, IK) - 1_IK)
258[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
259F, F, F, T
260call setPolyRoot(root, count, coef, eigen)
261count
262+5
263root(1:count)
264+0.999999642, +0.00000000,
265-0.429153442E-4, +1.00021696,
266-0.429153442E-4, -1.00021696,
267+0.427067280E-4, +0.999782741,
268+0.427067280E-4, -0.999782741
269getPolyVal(coef, root(1:count))
270+0.114440918E-4, +0.00000000,
271+0.238418579E-5, -0.804837327E-6,
272+0.238418579E-5, +0.804837327E-6,
273+0.190734863E-5, -0.566709787E-6,
274+0.190734863E-5, +0.566709787E-6
275
276
277coef
278+8.0000000000000000,
279-8.0000000000000000,
280+16.000000000000000,
281-16.000000000000000,
282+8.0000000000000000,
283-8.0000000000000000
284call setResized(root, size(coef, 1, IK) - 1_IK)
285[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
286F, F, F, T
287call setPolyRoot(root, count, coef, eigen)
288count
289+5
290root(1:count)
291+0.99999999999999922, +0.0000000000000000,
292+0.95202123961968255E-9, +1.0000000121923602,
293+0.95202123961968255E-9, -1.0000000121923602,
294-0.95202196126464855E-9, +0.99999998780764010,
295-0.95202196126464855E-9, -0.99999998780764010
296getPolyVal(coef, root(1:count))
297+0.23980817331903381E-13, +0.0000000000000000,
298+0.26645352591003757E-14, -0.55147887586065774E-14,
299+0.26645352591003757E-14, +0.55147887586065774E-14,
300+0.35527136788005009E-14, -0.50706995570283210E-14,
301+0.35527136788005009E-14, +0.50706995570283210E-14
302
303
304coef
305+8.00000000000000000000000000000000000,
306-8.00000000000000000000000000000000000,
307+16.0000000000000000000000000000000000,
308-16.0000000000000000000000000000000000,
309+8.00000000000000000000000000000000000,
310-8.00000000000000000000000000000000000
311call setResized(root, size(coef, 1, IK) - 1_IK)
312[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
313F, F, F, T
314call setPolyRoot(root, count, coef, eigen)
315count
316+5
317root(1:count)
318+1.00000000000000000000000000000000019, +0.00000000000000000000000000000000000,
319-0.108472542273474050653982053325797972E-16, +1.00000000000000000335355606599927526,
320-0.108472542273474050653982053325797972E-16, -1.00000000000000000335355606599927526,
321+0.108472542273474053061394483809842788E-16, +0.999999999999999996646443934000722236,
322+0.108472542273474053061394483809842788E-16, -0.999999999999999996646443934000722236
323getPolyVal(coef, root(1:count))
324-0.770371977754894341222391177033970927E-32, +0.00000000000000000000000000000000000,
325-0.308148791101957736488956470813588371E-32, +0.635981983657862231619686642857405375E-32,
326-0.308148791101957736488956470813588371E-32, -0.635981983657862231619686642857405375E-32,
327-0.308148791101957736488956470813588371E-32, +0.597463384770117558391908329517715426E-32,
328-0.308148791101957736488956470813588371E-32, -0.597463384770117558391908329517715426E-32
329
330
331!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
332! Compute the roots of polynomials with real coefficients.
333!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
334
335
336coef
337+3628800.00,
338-10628640.0,
339+12753576.0,
340-8409500.00,
341+3416930.00,
342-902055.000,
343+157773.000,
344-18150.0000,
345+1320.00000,
346-55.0000000,
347+1.00000000
348call setResized(root, size(coef, 1, IK) - 1_IK)
349[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
350T, F, F, F
351call setPolyRoot(root, count, coef, eigen)
352count
353+10
354root(1:count)
355+9.70840931, +0.304670960,
356+9.70840931, -0.304670960,
357+7.47363091, +0.879458010,
358+7.47363091, -0.879458010,
359+5.34100008, +0.00000000,
360+5.26379681, +0.00000000,
361+4.04746771, +0.00000000,
362+2.98188233, +0.00000000,
363+2.00178838, +0.00000000,
364+0.999977231, +0.00000000
365getPolyVal(coef, root(1:count))
366-68181.5000, -14448.8984,
367-68181.5000, +14448.8984,
368-8617.75000, -8708.84375,
369-8617.75000, +8708.84375,
370-810.250000, +0.00000000,
371-735.250000, +0.00000000,
372+180.500000, +0.00000000,
373+180.250000, +0.00000000,
374+72.2500000, +0.00000000,
375+8.25000000, +0.00000000
376
377
378coef
379+3628800.0000000000,
380-10628640.000000000,
381+12753576.000000000,
382-8409500.0000000000,
383+3416930.0000000000,
384-902055.00000000000,
385+157773.00000000000,
386-18150.000000000000,
387+1320.0000000000000,
388-55.000000000000000,
389+1.0000000000000000
390call setResized(root, size(coef, 1, IK) - 1_IK)
391[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
392T, F, F, F
393call setPolyRoot(root, count, coef, eigen)
394count
395+10
396root(1:count)
397+10.000000000095149, +0.0000000000000000,
398+8.9999999996955644, +0.0000000000000000,
399+8.0000000003491696, +0.0000000000000000,
400+6.9999999998340323, +0.0000000000000000,
401+6.0000000000428484, +0.0000000000000000,
402+4.9999999999586162, +0.0000000000000000,
403+4.0000000000353024, +0.0000000000000000,
404+2.9999999999877933, +0.0000000000000000,
405+2.0000000000016263, +0.0000000000000000,
406+0.99999999999994482, +0.0000000000000000
407getPolyVal(coef, root(1:count))
408+0.19303057342767715E-4, +0.0000000000000000,
409+0.10346993803977966E-4, +0.0000000000000000,
410+0.66170468926429749E-5, +0.0000000000000000,
411+0.89593231678009033E-6, +0.0000000000000000,
412-0.75763091444969177E-6, +0.0000000000000000,
413+0.10197982192039490E-6, +0.0000000000000000,
414+0.14528632164001465E-6, +0.0000000000000000,
415+0.85681676864624023E-7, +0.0000000000000000,
416+0.70314854383468628E-7, +0.0000000000000000,
417+0.19557774066925049E-7, +0.0000000000000000
418
419
420coef
421+3628800.00000000000000000000000000000,
422-10628640.0000000000000000000000000000,
423+12753576.0000000000000000000000000000,
424-8409500.00000000000000000000000000000,
425+3416930.00000000000000000000000000000,
426-902055.000000000000000000000000000000,
427+157773.000000000000000000000000000000,
428-18150.0000000000000000000000000000000,
429+1320.00000000000000000000000000000000,
430-55.0000000000000000000000000000000000,
431+1.00000000000000000000000000000000000
432call setResized(root, size(coef, 1, IK) - 1_IK)
433[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
434T, F, F, F
435call setPolyRoot(root, count, coef, eigen)
436count
437+10
438root(1:count)
439+10.0000000000000000000000000000517967, +0.00000000000000000000000000000000000,
440+8.99999999999999999999999999958200849, +0.00000000000000000000000000000000000,
441+8.00000000000000000000000000123870575, +0.00000000000000000000000000000000000,
442+6.99999999999999999999999999814682938, +0.00000000000000000000000000000000000,
443+6.00000000000000000000000000155546576, +0.00000000000000000000000000000000000,
444+4.99999999999999999999999999924843974, +0.00000000000000000000000000000000000,
445+4.00000000000000000000000000020351610, +0.00000000000000000000000000000000000,
446+2.99999999999999999999999999997156942, +0.00000000000000000000000000000000000,
447+2.00000000000000000000000000000172640, +0.00000000000000000000000000000000000,
448+0.999999999999999999999999999999968030, +0.00000000000000000000000000000000000
449getPolyVal(coef, root(1:count))
450+0.190570619346140160075476935146177038E-22, +0.00000000000000000000000000000000000,
451+0.106701452257938892161879271616720111E-22, +0.00000000000000000000000000000000000,
452+0.119020304153870212515188824892176100E-22, +0.00000000000000000000000000000000000,
453+0.954246540633683195630463953068600702E-23, +0.00000000000000000000000000000000000,
454+0.456645703394752484965632161745263673E-23, +0.00000000000000000000000000000000000,
455+0.212247759715144552316858040860725332E-23, +0.00000000000000000000000000000000000,
456+0.846163761376266102956836528264927821E-24, +0.00000000000000000000000000000000000,
457+0.307365452223073271766182624348262564E-24, +0.00000000000000000000000000000000000,
458+0.666429692730710773211828291950897807E-25, +0.00000000000000000000000000000000000,
459+0.117130067207215832867533457373188099E-25, +0.00000000000000000000000000000000000
460
461
462coef
463+3628800.00,
464-10628640.0,
465+12753576.0,
466-8409500.00,
467+3416930.00,
468-902055.000,
469+157773.000,
470-18150.0000,
471+1320.00000,
472-55.0000000,
473+1.00000000
474call setResized(root, size(coef, 1, IK) - 1_IK)
475[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
476F, T, F, F
477call setPolyRoot(root, count, coef, eigen)
478count
479+10
480root(1:count)
481+9.70840931, +0.304670960,
482+9.70840931, -0.304670960,
483+7.47363091, +0.879458010,
484+7.47363091, -0.879458010,
485+5.34100008, +0.00000000,
486+5.26379681, +0.00000000,
487+4.04746771, +0.00000000,
488+2.98188233, +0.00000000,
489+2.00178838, +0.00000000,
490+0.999977231, +0.00000000
491getPolyVal(coef, root(1:count))
492-68181.5000, -14448.8984,
493-68181.5000, +14448.8984,
494-8617.75000, -8708.84375,
495-8617.75000, +8708.84375,
496-810.250000, +0.00000000,
497-735.250000, +0.00000000,
498+180.500000, +0.00000000,
499+180.250000, +0.00000000,
500+72.2500000, +0.00000000,
501+8.25000000, +0.00000000
502
503
504coef
505+3628800.0000000000,
506-10628640.000000000,
507+12753576.000000000,
508-8409500.0000000000,
509+3416930.0000000000,
510-902055.00000000000,
511+157773.00000000000,
512-18150.000000000000,
513+1320.0000000000000,
514-55.000000000000000,
515+1.0000000000000000
516call setResized(root, size(coef, 1, IK) - 1_IK)
517[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
518F, T, F, F
519call setPolyRoot(root, count, coef, eigen)
520count
521+10
522root(1:count)
523+10.000000000095149, +0.0000000000000000,
524+8.9999999996955644, +0.0000000000000000,
525+8.0000000003491696, +0.0000000000000000,
526+6.9999999998340323, +0.0000000000000000,
527+6.0000000000428484, +0.0000000000000000,
528+4.9999999999586162, +0.0000000000000000,
529+4.0000000000353024, +0.0000000000000000,
530+2.9999999999877933, +0.0000000000000000,
531+2.0000000000016263, +0.0000000000000000,
532+0.99999999999994482, +0.0000000000000000
533getPolyVal(coef, root(1:count))
534+0.19303057342767715E-4, +0.0000000000000000,
535+0.10346993803977966E-4, +0.0000000000000000,
536+0.66170468926429749E-5, +0.0000000000000000,
537+0.89593231678009033E-6, +0.0000000000000000,
538-0.75763091444969177E-6, +0.0000000000000000,
539+0.10197982192039490E-6, +0.0000000000000000,
540+0.14528632164001465E-6, +0.0000000000000000,
541+0.85681676864624023E-7, +0.0000000000000000,
542+0.70314854383468628E-7, +0.0000000000000000,
543+0.19557774066925049E-7, +0.0000000000000000
544
545
546coef
547+3628800.00000000000000000000000000000,
548-10628640.0000000000000000000000000000,
549+12753576.0000000000000000000000000000,
550-8409500.00000000000000000000000000000,
551+3416930.00000000000000000000000000000,
552-902055.000000000000000000000000000000,
553+157773.000000000000000000000000000000,
554-18150.0000000000000000000000000000000,
555+1320.00000000000000000000000000000000,
556-55.0000000000000000000000000000000000,
557+1.00000000000000000000000000000000000
558call setResized(root, size(coef, 1, IK) - 1_IK)
559[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
560F, T, F, F
561call setPolyRoot(root, count, coef, eigen)
562count
563+10
564root(1:count)
565+10.0000000000000000000000000000517967, +0.00000000000000000000000000000000000,
566+8.99999999999999999999999999958200849, +0.00000000000000000000000000000000000,
567+8.00000000000000000000000000123870575, +0.00000000000000000000000000000000000,
568+6.99999999999999999999999999814682938, +0.00000000000000000000000000000000000,
569+6.00000000000000000000000000155546576, +0.00000000000000000000000000000000000,
570+4.99999999999999999999999999924843974, +0.00000000000000000000000000000000000,
571+4.00000000000000000000000000020351610, +0.00000000000000000000000000000000000,
572+2.99999999999999999999999999997156942, +0.00000000000000000000000000000000000,
573+2.00000000000000000000000000000172640, +0.00000000000000000000000000000000000,
574+0.999999999999999999999999999999968030, +0.00000000000000000000000000000000000
575getPolyVal(coef, root(1:count))
576+0.190570619346140160075476935146177038E-22, +0.00000000000000000000000000000000000,
577+0.106701452257938892161879271616720111E-22, +0.00000000000000000000000000000000000,
578+0.119020304153870212515188824892176100E-22, +0.00000000000000000000000000000000000,
579+0.954246540633683195630463953068600702E-23, +0.00000000000000000000000000000000000,
580+0.456645703394752484965632161745263673E-23, +0.00000000000000000000000000000000000,
581+0.212247759715144552316858040860725332E-23, +0.00000000000000000000000000000000000,
582+0.846163761376266102956836528264927821E-24, +0.00000000000000000000000000000000000,
583+0.307365452223073271766182624348262564E-24, +0.00000000000000000000000000000000000,
584+0.666429692730710773211828291950897807E-25, +0.00000000000000000000000000000000000,
585+0.117130067207215832867533457373188099E-25, +0.00000000000000000000000000000000000
586
587
588coef
589+3628800.00,
590-10628640.0,
591+12753576.0,
592-8409500.00,
593+3416930.00,
594-902055.000,
595+157773.000,
596-18150.0000,
597+1320.00000,
598-55.0000000,
599+1.00000000
600call setResized(root, size(coef, 1, IK) - 1_IK)
601[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
602F, F, T, F
603call setPolyRoot(root, count, coef, eigen)
604count
605+10
606root(1:count)
607+9.70840931, +0.304670960,
608+9.70840931, -0.304670960,
609+7.47363091, +0.879458010,
610+7.47363091, -0.879458010,
611+5.34100008, +0.00000000,
612+5.26379681, +0.00000000,
613+4.04746771, +0.00000000,
614+2.98188233, +0.00000000,
615+2.00178838, +0.00000000,
616+0.999977231, +0.00000000
617getPolyVal(coef, root(1:count))
618-68181.5000, -14448.8984,
619-68181.5000, +14448.8984,
620-8617.75000, -8708.84375,
621-8617.75000, +8708.84375,
622-810.250000, +0.00000000,
623-735.250000, +0.00000000,
624+180.500000, +0.00000000,
625+180.250000, +0.00000000,
626+72.2500000, +0.00000000,
627+8.25000000, +0.00000000
628
629
630coef
631+3628800.0000000000,
632-10628640.000000000,
633+12753576.000000000,
634-8409500.0000000000,
635+3416930.0000000000,
636-902055.00000000000,
637+157773.00000000000,
638-18150.000000000000,
639+1320.0000000000000,
640-55.000000000000000,
641+1.0000000000000000
642call setResized(root, size(coef, 1, IK) - 1_IK)
643[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
644F, F, T, F
645call setPolyRoot(root, count, coef, eigen)
646count
647+10
648root(1:count)
649+10.000000000095149, +0.0000000000000000,
650+8.9999999996955644, +0.0000000000000000,
651+8.0000000003491696, +0.0000000000000000,
652+6.9999999998340323, +0.0000000000000000,
653+6.0000000000428484, +0.0000000000000000,
654+4.9999999999586162, +0.0000000000000000,
655+4.0000000000353024, +0.0000000000000000,
656+2.9999999999877933, +0.0000000000000000,
657+2.0000000000016263, +0.0000000000000000,
658+0.99999999999994482, +0.0000000000000000
659getPolyVal(coef, root(1:count))
660+0.19303057342767715E-4, +0.0000000000000000,
661+0.10346993803977966E-4, +0.0000000000000000,
662+0.66170468926429749E-5, +0.0000000000000000,
663+0.89593231678009033E-6, +0.0000000000000000,
664-0.75763091444969177E-6, +0.0000000000000000,
665+0.10197982192039490E-6, +0.0000000000000000,
666+0.14528632164001465E-6, +0.0000000000000000,
667+0.85681676864624023E-7, +0.0000000000000000,
668+0.70314854383468628E-7, +0.0000000000000000,
669+0.19557774066925049E-7, +0.0000000000000000
670
671
672coef
673+3628800.00000000000000000000000000000,
674-10628640.0000000000000000000000000000,
675+12753576.0000000000000000000000000000,
676-8409500.00000000000000000000000000000,
677+3416930.00000000000000000000000000000,
678-902055.000000000000000000000000000000,
679+157773.000000000000000000000000000000,
680-18150.0000000000000000000000000000000,
681+1320.00000000000000000000000000000000,
682-55.0000000000000000000000000000000000,
683+1.00000000000000000000000000000000000
684call setResized(root, size(coef, 1, IK) - 1_IK)
685[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
686F, F, T, F
687call setPolyRoot(root, count, coef, eigen)
688count
689+10
690root(1:count)
691+10.0000000000000000000000000000517967, +0.00000000000000000000000000000000000,
692+8.99999999999999999999999999958200849, +0.00000000000000000000000000000000000,
693+8.00000000000000000000000000123870575, +0.00000000000000000000000000000000000,
694+6.99999999999999999999999999814682938, +0.00000000000000000000000000000000000,
695+6.00000000000000000000000000155546576, +0.00000000000000000000000000000000000,
696+4.99999999999999999999999999924843974, +0.00000000000000000000000000000000000,
697+4.00000000000000000000000000020351610, +0.00000000000000000000000000000000000,
698+2.99999999999999999999999999997156942, +0.00000000000000000000000000000000000,
699+2.00000000000000000000000000000172640, +0.00000000000000000000000000000000000,
700+0.999999999999999999999999999999968030, +0.00000000000000000000000000000000000
701getPolyVal(coef, root(1:count))
702+0.190570619346140160075476935146177038E-22, +0.00000000000000000000000000000000000,
703+0.106701452257938892161879271616720111E-22, +0.00000000000000000000000000000000000,
704+0.119020304153870212515188824892176100E-22, +0.00000000000000000000000000000000000,
705+0.954246540633683195630463953068600702E-23, +0.00000000000000000000000000000000000,
706+0.456645703394752484965632161745263673E-23, +0.00000000000000000000000000000000000,
707+0.212247759715144552316858040860725332E-23, +0.00000000000000000000000000000000000,
708+0.846163761376266102956836528264927821E-24, +0.00000000000000000000000000000000000,
709+0.307365452223073271766182624348262564E-24, +0.00000000000000000000000000000000000,
710+0.666429692730710773211828291950897807E-25, +0.00000000000000000000000000000000000,
711+0.117130067207215832867533457373188099E-25, +0.00000000000000000000000000000000000
712
713
714coef
715+3628800.00,
716-10628640.0,
717+12753576.0,
718-8409500.00,
719+3416930.00,
720-902055.000,
721+157773.000,
722-18150.0000,
723+1320.00000,
724-55.0000000,
725+1.00000000
726call setResized(root, size(coef, 1, IK) - 1_IK)
727[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
728F, F, F, T
729call setPolyRoot(root, count, coef, eigen)
730count
731+10
732root(1:count)
733+9.70840931, +0.304670960,
734+9.70840931, -0.304670960,
735+7.47363091, +0.879458010,
736+7.47363091, -0.879458010,
737+5.34100008, +0.00000000,
738+5.26379681, +0.00000000,
739+4.04746771, +0.00000000,
740+2.98188233, +0.00000000,
741+2.00178838, +0.00000000,
742+0.999977231, +0.00000000
743getPolyVal(coef, root(1:count))
744-68181.5000, -14448.8984,
745-68181.5000, +14448.8984,
746-8617.75000, -8708.84375,
747-8617.75000, +8708.84375,
748-810.250000, +0.00000000,
749-735.250000, +0.00000000,
750+180.500000, +0.00000000,
751+180.250000, +0.00000000,
752+72.2500000, +0.00000000,
753+8.25000000, +0.00000000
754
755
756coef
757+3628800.0000000000,
758-10628640.000000000,
759+12753576.000000000,
760-8409500.0000000000,
761+3416930.0000000000,
762-902055.00000000000,
763+157773.00000000000,
764-18150.000000000000,
765+1320.0000000000000,
766-55.000000000000000,
767+1.0000000000000000
768call setResized(root, size(coef, 1, IK) - 1_IK)
769[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
770F, F, F, T
771call setPolyRoot(root, count, coef, eigen)
772count
773+10
774root(1:count)
775+10.000000000095149, +0.0000000000000000,
776+8.9999999996955644, +0.0000000000000000,
777+8.0000000003491696, +0.0000000000000000,
778+6.9999999998340323, +0.0000000000000000,
779+6.0000000000428484, +0.0000000000000000,
780+4.9999999999586162, +0.0000000000000000,
781+4.0000000000353024, +0.0000000000000000,
782+2.9999999999877933, +0.0000000000000000,
783+2.0000000000016263, +0.0000000000000000,
784+0.99999999999994482, +0.0000000000000000
785getPolyVal(coef, root(1:count))
786+0.19303057342767715E-4, +0.0000000000000000,
787+0.10346993803977966E-4, +0.0000000000000000,
788+0.66170468926429749E-5, +0.0000000000000000,
789+0.89593231678009033E-6, +0.0000000000000000,
790-0.75763091444969177E-6, +0.0000000000000000,
791+0.10197982192039490E-6, +0.0000000000000000,
792+0.14528632164001465E-6, +0.0000000000000000,
793+0.85681676864624023E-7, +0.0000000000000000,
794+0.70314854383468628E-7, +0.0000000000000000,
795+0.19557774066925049E-7, +0.0000000000000000
796
797
798coef
799+3628800.00000000000000000000000000000,
800-10628640.0000000000000000000000000000,
801+12753576.0000000000000000000000000000,
802-8409500.00000000000000000000000000000,
803+3416930.00000000000000000000000000000,
804-902055.000000000000000000000000000000,
805+157773.000000000000000000000000000000,
806-18150.0000000000000000000000000000000,
807+1320.00000000000000000000000000000000,
808-55.0000000000000000000000000000000000,
809+1.00000000000000000000000000000000000
810call setResized(root, size(coef, 1, IK) - 1_IK)
811[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
812F, F, F, T
813call setPolyRoot(root, count, coef, eigen)
814count
815+10
816root(1:count)
817+10.0000000000000000000000000000517967, +0.00000000000000000000000000000000000,
818+8.99999999999999999999999999958200849, +0.00000000000000000000000000000000000,
819+8.00000000000000000000000000123870575, +0.00000000000000000000000000000000000,
820+6.99999999999999999999999999814682938, +0.00000000000000000000000000000000000,
821+6.00000000000000000000000000155546576, +0.00000000000000000000000000000000000,
822+4.99999999999999999999999999924843974, +0.00000000000000000000000000000000000,
823+4.00000000000000000000000000020351610, +0.00000000000000000000000000000000000,
824+2.99999999999999999999999999997156942, +0.00000000000000000000000000000000000,
825+2.00000000000000000000000000000172640, +0.00000000000000000000000000000000000,
826+0.999999999999999999999999999999968030, +0.00000000000000000000000000000000000
827getPolyVal(coef, root(1:count))
828+0.190570619346140160075476935146177038E-22, +0.00000000000000000000000000000000000,
829+0.106701452257938892161879271616720111E-22, +0.00000000000000000000000000000000000,
830+0.119020304153870212515188824892176100E-22, +0.00000000000000000000000000000000000,
831+0.954246540633683195630463953068600702E-23, +0.00000000000000000000000000000000000,
832+0.456645703394752484965632161745263673E-23, +0.00000000000000000000000000000000000,
833+0.212247759715144552316858040860725332E-23, +0.00000000000000000000000000000000000,
834+0.846163761376266102956836528264927821E-24, +0.00000000000000000000000000000000000,
835+0.307365452223073271766182624348262564E-24, +0.00000000000000000000000000000000000,
836+0.666429692730710773211828291950897807E-25, +0.00000000000000000000000000000000000,
837+0.117130067207215832867533457373188099E-25, +0.00000000000000000000000000000000000
838
839
840!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
841! Compute the roots of polynomials with complex coefficients with zeros 1,2,...,10.
842!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
843
844
845coef
846+3628800.00, +0.00000000,
847-10628640.0, +0.00000000,
848+12753576.0, +0.00000000,
849-8409500.00, +0.00000000,
850+3416930.00, +0.00000000,
851-902055.000, +0.00000000,
852+157773.000, +0.00000000,
853-18150.0000, +0.00000000,
854+1320.00000, +0.00000000,
855-55.0000000, +0.00000000,
856+1.00000000, +0.00000000
857call setResized(root, size(coef, 1, IK) - 1_IK)
858[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
859T, F, F, F
860call setPolyRoot(root, count, coef, eigen)
861count
862+10
863root(1:count)
864+9.99373722, +0.196921639E-2,
865+9.07808781, -0.768133765E-2,
866+7.58786488, +0.259252965,
867+7.53517246, -0.258893400,
868+5.48630047, +0.496490821E-1,
869+5.36296797, -0.451893099E-1,
870+3.94950104, +0.102348044E-2,
871+3.00655532, -0.139494587E-3,
872+1.99981821, +0.898552662E-5,
873+0.999996662, -0.528134251E-6
874getPolyVal(coef, root(1:count))
875-4153.50000, +685.126953,
876+1293.75000, +363.354248,
877-3629.75000, -342.171875,
878-2187.25000, +294.710938,
879-1123.75000, -18.1875000,
880-459.750000, +35.3359375,
881-246.750000, +4.63513184,
882-61.2500000, +1.38377380,
883-6.00000000, +0.362543106,
884+0.500000000, +0.191653848
885
886
887coef
888+3628800.0000000000, +0.0000000000000000,
889-10628640.000000000, +0.0000000000000000,
890+12753576.000000000, +0.0000000000000000,
891-8409500.0000000000, +0.0000000000000000,
892+3416930.0000000000, +0.0000000000000000,
893-902055.00000000000, +0.0000000000000000,
894+157773.00000000000, +0.0000000000000000,
895-18150.000000000000, +0.0000000000000000,
896+1320.0000000000000, +0.0000000000000000,
897-55.000000000000000, +0.0000000000000000,
898+1.0000000000000000, +0.0000000000000000
899call setResized(root, size(coef, 1, IK) - 1_IK)
900[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
901T, F, F, F
902call setPolyRoot(root, count, coef, eigen)
903count
904+10
905root(1:count)
906+10.000000000092832, +0.14674683172918083E-11,
907+8.9999999995494910, -0.78513163716371057E-11,
908+8.0000000009219665, +0.18126945817416554E-10,
909+6.9999999989793631, -0.23471195338655758E-10,
910+6.0000000006482752, +0.18575051340220250E-10,
911+4.9999999997713829, -0.92418512141289470E-11,
912+4.0000000000382663, +0.28926396100133261E-11,
913+2.9999999999985825, -0.54892097595564787E-12,
914+1.9999999999998195, +0.51688262166740718E-13,
915+1.0000000000000040, -0.69823506140973722E-15
916getPolyVal(coef, root(1:count))
917+0.21335668861865997E-4, +0.53251490324658425E-6,
918+0.15214085578918457E-4, +0.31656507562992751E-6,
919+0.12007541954517365E-4, +0.18271961426412876E-6,
920+0.43502077460289001E-5, +0.10139556374739953E-6,
921+0.16265548765659332E-5, +0.53496147868086052E-7,
922+0.96531584858894348E-6, +0.26616531495547122E-7,
923+0.16111880540847778E-6, +0.12496203114631699E-7,
924-0.93132257461547852E-9, +0.55331234376599884E-8,
925-0.79162418842315674E-8, +0.20840707305641930E-8,
926-0.23283064365386963E-8, +0.25337553908436255E-9
927
928
929coef
930+3628800.00000000000000000000000000000, +0.00000000000000000000000000000000000,
931-10628640.0000000000000000000000000000, +0.00000000000000000000000000000000000,
932+12753576.0000000000000000000000000000, +0.00000000000000000000000000000000000,
933-8409500.00000000000000000000000000000, +0.00000000000000000000000000000000000,
934+3416930.00000000000000000000000000000, +0.00000000000000000000000000000000000,
935-902055.000000000000000000000000000000, +0.00000000000000000000000000000000000,
936+157773.000000000000000000000000000000, +0.00000000000000000000000000000000000,
937-18150.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
938+1320.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
939-55.0000000000000000000000000000000000, +0.00000000000000000000000000000000000,
940+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
941call setResized(root, size(coef, 1, IK) - 1_IK)
942[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
943T, F, F, F
944call setPolyRoot(root, count, coef, eigen)
945count
946+10
947root(1:count)
948+10.0000000000000000000000000001225200, +0.509435088823196545261926980817026425E-30,
949+8.99999999999999999999999999940435917, -0.209995537749767662358226781607926446E-29,
950+8.00000000000000000000000000121674245, +0.343592927705395245870133814335134133E-29,
951+6.99999999999999999999999999865599133, -0.302445729136684007599014761793556296E-29,
952+6.00000000000000000000000000086041537, +0.192719830774026860653879227602749694E-29,
953+4.99999999999999999999999999968191341, -0.123024474772112043974718002090415763E-29,
954+4.00000000000000000000000000006421590, +0.652456748571305541599111900496149722E-30,
955+2.99999999999999999999999999999352079, -0.193766393931633696713588827264264386E-30,
956+2.00000000000000000000000000000033781, +0.237223756726557254262497294342951649E-31,
957+0.999999999999999999999999999999990659, -0.651188212631313945515795127577401738E-33
958getPolyVal(coef, root(1:count))
959+0.382902228668223289224410580203206145E-22, +0.184863805032161562344648062924845379E-24,
960+0.258530292133333732621308588724151623E-22, +0.846702008207063214628370381684629456E-25,
961+0.141743537192070084091490315622574592E-22, +0.346341671127038407837094885825177763E-25,
962+0.442428536616497321803779824850311186E-23, +0.130656554987047491282774376921933986E-25,
963+0.197545916796721599501760737935263101E-23, +0.555033112629197358683172175557306576E-26,
964+0.891804097908732961970737496137928702E-24, +0.354310487343682686647187846065246503E-26,
965+0.246780934702099565110561870534544582E-24, +0.281861315382803993970816340989114052E-26,
966+0.727014210251684479867449045764615789E-25, +0.195316525083086766287297537885110653E-26,
967+0.137324906380873735086073708644427427E-25, +0.956486187121478849186389090789675841E-27,
968+0.323117426778526435496644020339829240E-26, +0.236303178599651204548771735895300922E-27
969
970
971coef
972+3628800.00, +0.00000000,
973-10628640.0, +0.00000000,
974+12753576.0, +0.00000000,
975-8409500.00, +0.00000000,
976+3416930.00, +0.00000000,
977-902055.000, +0.00000000,
978+157773.000, +0.00000000,
979-18150.0000, +0.00000000,
980+1320.00000, +0.00000000,
981-55.0000000, +0.00000000,
982+1.00000000, +0.00000000
983call setResized(root, size(coef, 1, IK) - 1_IK)
984[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
985F, T, F, F
986call setPolyRoot(root, count, coef, eigen)
987count
988+10
989root(1:count)
990+9.99373722, +0.196921639E-2,
991+9.07808781, -0.768133765E-2,
992+7.58786488, +0.259252965,
993+7.53517246, -0.258893400,
994+5.48630047, +0.496490821E-1,
995+5.36296797, -0.451893099E-1,
996+3.94950104, +0.102348044E-2,
997+3.00655532, -0.139494587E-3,
998+1.99981821, +0.898552662E-5,
999+0.999996662, -0.528134251E-6
1000getPolyVal(coef, root(1:count))
1001-4153.50000, +685.126953,
1002+1293.75000, +363.354248,
1003-3629.75000, -342.171875,
1004-2187.25000, +294.710938,
1005-1123.75000, -18.1875000,
1006-459.750000, +35.3359375,
1007-246.750000, +4.63513184,
1008-61.2500000, +1.38377380,
1009-6.00000000, +0.362543106,
1010+0.500000000, +0.191653848
1011
1012
1013coef
1014+3628800.0000000000, +0.0000000000000000,
1015-10628640.000000000, +0.0000000000000000,
1016+12753576.000000000, +0.0000000000000000,
1017-8409500.0000000000, +0.0000000000000000,
1018+3416930.0000000000, +0.0000000000000000,
1019-902055.00000000000, +0.0000000000000000,
1020+157773.00000000000, +0.0000000000000000,
1021-18150.000000000000, +0.0000000000000000,
1022+1320.0000000000000, +0.0000000000000000,
1023-55.000000000000000, +0.0000000000000000,
1024+1.0000000000000000, +0.0000000000000000
1025call setResized(root, size(coef, 1, IK) - 1_IK)
1026[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1027F, T, F, F
1028call setPolyRoot(root, count, coef, eigen)
1029count
1030+10
1031root(1:count)
1032+10.000000000092832, +0.14674683172918083E-11,
1033+8.9999999995494910, -0.78513163716371057E-11,
1034+8.0000000009219665, +0.18126945817416554E-10,
1035+6.9999999989793631, -0.23471195338655758E-10,
1036+6.0000000006482752, +0.18575051340220250E-10,
1037+4.9999999997713829, -0.92418512141289470E-11,
1038+4.0000000000382663, +0.28926396100133261E-11,
1039+2.9999999999985825, -0.54892097595564787E-12,
1040+1.9999999999998195, +0.51688262166740718E-13,
1041+1.0000000000000040, -0.69823506140973722E-15
1042getPolyVal(coef, root(1:count))
1043+0.21335668861865997E-4, +0.53251490324658425E-6,
1044+0.15214085578918457E-4, +0.31656507562992751E-6,
1045+0.12007541954517365E-4, +0.18271961426412876E-6,
1046+0.43502077460289001E-5, +0.10139556374739953E-6,
1047+0.16265548765659332E-5, +0.53496147868086052E-7,
1048+0.96531584858894348E-6, +0.26616531495547122E-7,
1049+0.16111880540847778E-6, +0.12496203114631699E-7,
1050-0.93132257461547852E-9, +0.55331234376599884E-8,
1051-0.79162418842315674E-8, +0.20840707305641930E-8,
1052-0.23283064365386963E-8, +0.25337553908436255E-9
1053
1054
1055coef
1056+3628800.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1057-10628640.0000000000000000000000000000, +0.00000000000000000000000000000000000,
1058+12753576.0000000000000000000000000000, +0.00000000000000000000000000000000000,
1059-8409500.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1060+3416930.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1061-902055.000000000000000000000000000000, +0.00000000000000000000000000000000000,
1062+157773.000000000000000000000000000000, +0.00000000000000000000000000000000000,
1063-18150.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
1064+1320.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
1065-55.0000000000000000000000000000000000, +0.00000000000000000000000000000000000,
1066+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1067call setResized(root, size(coef, 1, IK) - 1_IK)
1068[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1069F, T, F, F
1070call setPolyRoot(root, count, coef, eigen)
1071count
1072+10
1073root(1:count)
1074+10.0000000000000000000000000001225200, +0.509435088823196545261926980817026425E-30,
1075+8.99999999999999999999999999940435917, -0.209995537749767662358226781607926446E-29,
1076+8.00000000000000000000000000121674245, +0.343592927705395245870133814335134133E-29,
1077+6.99999999999999999999999999865599133, -0.302445729136684007599014761793556296E-29,
1078+6.00000000000000000000000000086041537, +0.192719830774026860653879227602749694E-29,
1079+4.99999999999999999999999999968191341, -0.123024474772112043974718002090415763E-29,
1080+4.00000000000000000000000000006421590, +0.652456748571305541599111900496149722E-30,
1081+2.99999999999999999999999999999352079, -0.193766393931633696713588827264264386E-30,
1082+2.00000000000000000000000000000033781, +0.237223756726557254262497294342951649E-31,
1083+0.999999999999999999999999999999990659, -0.651188212631313945515795127577401738E-33
1084getPolyVal(coef, root(1:count))
1085+0.382902228668223289224410580203206145E-22, +0.184863805032161562344648062924845379E-24,
1086+0.258530292133333732621308588724151623E-22, +0.846702008207063214628370381684629456E-25,
1087+0.141743537192070084091490315622574592E-22, +0.346341671127038407837094885825177763E-25,
1088+0.442428536616497321803779824850311186E-23, +0.130656554987047491282774376921933986E-25,
1089+0.197545916796721599501760737935263101E-23, +0.555033112629197358683172175557306576E-26,
1090+0.891804097908732961970737496137928702E-24, +0.354310487343682686647187846065246503E-26,
1091+0.246780934702099565110561870534544582E-24, +0.281861315382803993970816340989114052E-26,
1092+0.727014210251684479867449045764615789E-25, +0.195316525083086766287297537885110653E-26,
1093+0.137324906380873735086073708644427427E-25, +0.956486187121478849186389090789675841E-27,
1094+0.323117426778526435496644020339829240E-26, +0.236303178599651204548771735895300922E-27
1095
1096
1097coef
1098+3628800.00, +0.00000000,
1099-10628640.0, +0.00000000,
1100+12753576.0, +0.00000000,
1101-8409500.00, +0.00000000,
1102+3416930.00, +0.00000000,
1103-902055.000, +0.00000000,
1104+157773.000, +0.00000000,
1105-18150.0000, +0.00000000,
1106+1320.00000, +0.00000000,
1107-55.0000000, +0.00000000,
1108+1.00000000, +0.00000000
1109call setResized(root, size(coef, 1, IK) - 1_IK)
1110[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1111F, F, T, F
1112call setPolyRoot(root, count, coef, eigen)
1113count
1114+10
1115root(1:count)
1116+9.99373722, +0.196921639E-2,
1117+9.07808781, -0.768133765E-2,
1118+7.58786488, +0.259252965,
1119+7.53517246, -0.258893400,
1120+5.48630047, +0.496490821E-1,
1121+5.36296797, -0.451893099E-1,
1122+3.94950104, +0.102348044E-2,
1123+3.00655532, -0.139494587E-3,
1124+1.99981821, +0.898552662E-5,
1125+0.999996662, -0.528134251E-6
1126getPolyVal(coef, root(1:count))
1127-4153.50000, +685.126953,
1128+1293.75000, +363.354248,
1129-3629.75000, -342.171875,
1130-2187.25000, +294.710938,
1131-1123.75000, -18.1875000,
1132-459.750000, +35.3359375,
1133-246.750000, +4.63513184,
1134-61.2500000, +1.38377380,
1135-6.00000000, +0.362543106,
1136+0.500000000, +0.191653848
1137
1138
1139coef
1140+3628800.0000000000, +0.0000000000000000,
1141-10628640.000000000, +0.0000000000000000,
1142+12753576.000000000, +0.0000000000000000,
1143-8409500.0000000000, +0.0000000000000000,
1144+3416930.0000000000, +0.0000000000000000,
1145-902055.00000000000, +0.0000000000000000,
1146+157773.00000000000, +0.0000000000000000,
1147-18150.000000000000, +0.0000000000000000,
1148+1320.0000000000000, +0.0000000000000000,
1149-55.000000000000000, +0.0000000000000000,
1150+1.0000000000000000, +0.0000000000000000
1151call setResized(root, size(coef, 1, IK) - 1_IK)
1152[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1153F, F, T, F
1154call setPolyRoot(root, count, coef, eigen)
1155count
1156+10
1157root(1:count)
1158+10.000000000092832, +0.14674683172918083E-11,
1159+8.9999999995494910, -0.78513163716371057E-11,
1160+8.0000000009219665, +0.18126945817416554E-10,
1161+6.9999999989793631, -0.23471195338655758E-10,
1162+6.0000000006482752, +0.18575051340220250E-10,
1163+4.9999999997713829, -0.92418512141289470E-11,
1164+4.0000000000382663, +0.28926396100133261E-11,
1165+2.9999999999985825, -0.54892097595564787E-12,
1166+1.9999999999998195, +0.51688262166740718E-13,
1167+1.0000000000000040, -0.69823506140973722E-15
1168getPolyVal(coef, root(1:count))
1169+0.21335668861865997E-4, +0.53251490324658425E-6,
1170+0.15214085578918457E-4, +0.31656507562992751E-6,
1171+0.12007541954517365E-4, +0.18271961426412876E-6,
1172+0.43502077460289001E-5, +0.10139556374739953E-6,
1173+0.16265548765659332E-5, +0.53496147868086052E-7,
1174+0.96531584858894348E-6, +0.26616531495547122E-7,
1175+0.16111880540847778E-6, +0.12496203114631699E-7,
1176-0.93132257461547852E-9, +0.55331234376599884E-8,
1177-0.79162418842315674E-8, +0.20840707305641930E-8,
1178-0.23283064365386963E-8, +0.25337553908436255E-9
1179
1180
1181coef
1182+3628800.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1183-10628640.0000000000000000000000000000, +0.00000000000000000000000000000000000,
1184+12753576.0000000000000000000000000000, +0.00000000000000000000000000000000000,
1185-8409500.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1186+3416930.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1187-902055.000000000000000000000000000000, +0.00000000000000000000000000000000000,
1188+157773.000000000000000000000000000000, +0.00000000000000000000000000000000000,
1189-18150.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
1190+1320.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
1191-55.0000000000000000000000000000000000, +0.00000000000000000000000000000000000,
1192+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1193call setResized(root, size(coef, 1, IK) - 1_IK)
1194[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1195F, F, T, F
1196call setPolyRoot(root, count, coef, eigen)
1197count
1198+10
1199root(1:count)
1200+10.0000000000000000000000000001225200, +0.509435088823196545261926980817026425E-30,
1201+8.99999999999999999999999999940435917, -0.209995537749767662358226781607926446E-29,
1202+8.00000000000000000000000000121674245, +0.343592927705395245870133814335134133E-29,
1203+6.99999999999999999999999999865599133, -0.302445729136684007599014761793556296E-29,
1204+6.00000000000000000000000000086041537, +0.192719830774026860653879227602749694E-29,
1205+4.99999999999999999999999999968191341, -0.123024474772112043974718002090415763E-29,
1206+4.00000000000000000000000000006421590, +0.652456748571305541599111900496149722E-30,
1207+2.99999999999999999999999999999352079, -0.193766393931633696713588827264264386E-30,
1208+2.00000000000000000000000000000033781, +0.237223756726557254262497294342951649E-31,
1209+0.999999999999999999999999999999990659, -0.651188212631313945515795127577401738E-33
1210getPolyVal(coef, root(1:count))
1211+0.382902228668223289224410580203206145E-22, +0.184863805032161562344648062924845379E-24,
1212+0.258530292133333732621308588724151623E-22, +0.846702008207063214628370381684629456E-25,
1213+0.141743537192070084091490315622574592E-22, +0.346341671127038407837094885825177763E-25,
1214+0.442428536616497321803779824850311186E-23, +0.130656554987047491282774376921933986E-25,
1215+0.197545916796721599501760737935263101E-23, +0.555033112629197358683172175557306576E-26,
1216+0.891804097908732961970737496137928702E-24, +0.354310487343682686647187846065246503E-26,
1217+0.246780934702099565110561870534544582E-24, +0.281861315382803993970816340989114052E-26,
1218+0.727014210251684479867449045764615789E-25, +0.195316525083086766287297537885110653E-26,
1219+0.137324906380873735086073708644427427E-25, +0.956486187121478849186389090789675841E-27,
1220+0.323117426778526435496644020339829240E-26, +0.236303178599651204548771735895300922E-27
1221
1222
1223coef
1224+3628800.00, +0.00000000,
1225-10628640.0, +0.00000000,
1226+12753576.0, +0.00000000,
1227-8409500.00, +0.00000000,
1228+3416930.00, +0.00000000,
1229-902055.000, +0.00000000,
1230+157773.000, +0.00000000,
1231-18150.0000, +0.00000000,
1232+1320.00000, +0.00000000,
1233-55.0000000, +0.00000000,
1234+1.00000000, +0.00000000
1235call setResized(root, size(coef, 1, IK) - 1_IK)
1236[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1237F, F, F, T
1238call setPolyRoot(root, count, coef, eigen)
1239count
1240+10
1241root(1:count)
1242+9.99373722, +0.196921639E-2,
1243+9.07808781, -0.768133765E-2,
1244+7.58786488, +0.259252965,
1245+7.53517246, -0.258893400,
1246+5.48630047, +0.496490821E-1,
1247+5.36296797, -0.451893099E-1,
1248+3.94950104, +0.102348044E-2,
1249+3.00655532, -0.139494587E-3,
1250+1.99981821, +0.898552662E-5,
1251+0.999996662, -0.528134251E-6
1252getPolyVal(coef, root(1:count))
1253-4153.50000, +685.126953,
1254+1293.75000, +363.354248,
1255-3629.75000, -342.171875,
1256-2187.25000, +294.710938,
1257-1123.75000, -18.1875000,
1258-459.750000, +35.3359375,
1259-246.750000, +4.63513184,
1260-61.2500000, +1.38377380,
1261-6.00000000, +0.362543106,
1262+0.500000000, +0.191653848
1263
1264
1265coef
1266+3628800.0000000000, +0.0000000000000000,
1267-10628640.000000000, +0.0000000000000000,
1268+12753576.000000000, +0.0000000000000000,
1269-8409500.0000000000, +0.0000000000000000,
1270+3416930.0000000000, +0.0000000000000000,
1271-902055.00000000000, +0.0000000000000000,
1272+157773.00000000000, +0.0000000000000000,
1273-18150.000000000000, +0.0000000000000000,
1274+1320.0000000000000, +0.0000000000000000,
1275-55.000000000000000, +0.0000000000000000,
1276+1.0000000000000000, +0.0000000000000000
1277call setResized(root, size(coef, 1, IK) - 1_IK)
1278[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1279F, F, F, T
1280call setPolyRoot(root, count, coef, eigen)
1281count
1282+10
1283root(1:count)
1284+10.000000000092832, +0.14674683172918083E-11,
1285+8.9999999995494910, -0.78513163716371057E-11,
1286+8.0000000009219665, +0.18126945817416554E-10,
1287+6.9999999989793631, -0.23471195338655758E-10,
1288+6.0000000006482752, +0.18575051340220250E-10,
1289+4.9999999997713829, -0.92418512141289470E-11,
1290+4.0000000000382663, +0.28926396100133261E-11,
1291+2.9999999999985825, -0.54892097595564787E-12,
1292+1.9999999999998195, +0.51688262166740718E-13,
1293+1.0000000000000040, -0.69823506140973722E-15
1294getPolyVal(coef, root(1:count))
1295+0.21335668861865997E-4, +0.53251490324658425E-6,
1296+0.15214085578918457E-4, +0.31656507562992751E-6,
1297+0.12007541954517365E-4, +0.18271961426412876E-6,
1298+0.43502077460289001E-5, +0.10139556374739953E-6,
1299+0.16265548765659332E-5, +0.53496147868086052E-7,
1300+0.96531584858894348E-6, +0.26616531495547122E-7,
1301+0.16111880540847778E-6, +0.12496203114631699E-7,
1302-0.93132257461547852E-9, +0.55331234376599884E-8,
1303-0.79162418842315674E-8, +0.20840707305641930E-8,
1304-0.23283064365386963E-8, +0.25337553908436255E-9
1305
1306
1307coef
1308+3628800.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1309-10628640.0000000000000000000000000000, +0.00000000000000000000000000000000000,
1310+12753576.0000000000000000000000000000, +0.00000000000000000000000000000000000,
1311-8409500.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1312+3416930.00000000000000000000000000000, +0.00000000000000000000000000000000000,
1313-902055.000000000000000000000000000000, +0.00000000000000000000000000000000000,
1314+157773.000000000000000000000000000000, +0.00000000000000000000000000000000000,
1315-18150.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
1316+1320.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
1317-55.0000000000000000000000000000000000, +0.00000000000000000000000000000000000,
1318+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1319call setResized(root, size(coef, 1, IK) - 1_IK)
1320[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1321F, F, F, T
1322call setPolyRoot(root, count, coef, eigen)
1323count
1324+10
1325root(1:count)
1326+10.0000000000000000000000000001225200, +0.509435088823196545261926980817026425E-30,
1327+8.99999999999999999999999999940435917, -0.209995537749767662358226781607926446E-29,
1328+8.00000000000000000000000000121674245, +0.343592927705395245870133814335134133E-29,
1329+6.99999999999999999999999999865599133, -0.302445729136684007599014761793556296E-29,
1330+6.00000000000000000000000000086041537, +0.192719830774026860653879227602749694E-29,
1331+4.99999999999999999999999999968191341, -0.123024474772112043974718002090415763E-29,
1332+4.00000000000000000000000000006421590, +0.652456748571305541599111900496149722E-30,
1333+2.99999999999999999999999999999352079, -0.193766393931633696713588827264264386E-30,
1334+2.00000000000000000000000000000033781, +0.237223756726557254262497294342951649E-31,
1335+0.999999999999999999999999999999990659, -0.651188212631313945515795127577401738E-33
1336getPolyVal(coef, root(1:count))
1337+0.382902228668223289224410580203206145E-22, +0.184863805032161562344648062924845379E-24,
1338+0.258530292133333732621308588724151623E-22, +0.846702008207063214628370381684629456E-25,
1339+0.141743537192070084091490315622574592E-22, +0.346341671127038407837094885825177763E-25,
1340+0.442428536616497321803779824850311186E-23, +0.130656554987047491282774376921933986E-25,
1341+0.197545916796721599501760737935263101E-23, +0.555033112629197358683172175557306576E-26,
1342+0.891804097908732961970737496137928702E-24, +0.354310487343682686647187846065246503E-26,
1343+0.246780934702099565110561870534544582E-24, +0.281861315382803993970816340989114052E-26,
1344+0.727014210251684479867449045764615789E-25, +0.195316525083086766287297537885110653E-26,
1345+0.137324906380873735086073708644427427E-25, +0.956486187121478849186389090789675841E-27,
1346+0.323117426778526435496644020339829240E-26, +0.236303178599651204548771735895300922E-27
1347
1348
1349!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1350! Compute the roots of polynomials with complex coefficients with zeros on imaginary axis.
1351!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1352
1353
1354coef
1355+0.0000000000000000, +1.0000000000000000,
1356-10001.000099999999, +0.0000000000000000,
1357+0.0000000000000000, -10001.000099999999,
1358+1.0000000000000000, +0.0000000000000000
1359call setResized(root, size(coef, 1, IK) - 1_IK)
1360[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1361T, F, F, F
1362call setPolyRoot(root, count, coef, eigen)
1363count
1364+3
1365root(1:count)
1366+0.0000000000000000, +10000.000000000000,
1367+0.0000000000000000, +1.0000000000000004,
1368+0.0000000000000000, +0.10000000000000255E-3
1369getPolyVal(coef, root(1:count))
1370+0.0000000000000000, -0.70715235779061913E-4,
1371+0.0000000000000000, +0.36375347178818629E-11,
1372+0.0000000000000000, -0.25535129566378600E-13
1373
1374
1375coef
1376+0.00000000000000000000000000000000000, +1.00000000000000000000000000000000000,
1377-10001.0000999999999999999999999999996, +0.00000000000000000000000000000000000,
1378+0.00000000000000000000000000000000000, -10001.0000999999999999999999999999996,
1379+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1380call setResized(root, size(coef, 1, IK) - 1_IK)
1381[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1382T, F, F, F
1383call setPolyRoot(root, count, coef, eigen)
1384count
1385+3
1386root(1:count)
1387+0.00000000000000000000000000000000000, +9999.99999999999999999999999999999842,
1388+0.00000000000000000000000000000000000, +0.999999999999999999999999999999999904,
1389+0.00000000000000000000000000000000000, +0.100000000000000000000000000000000008E-3
1390getPolyVal(coef, root(1:count))
1391+0.00000000000000000000000000000000000, +0.115351482477835407341207567853721561E-21,
1392+0.00000000000000000000000000000000000, -0.157752921744758488723815153277131397E-29,
1393+0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1394
1395
1396coef
1397+0.0000000000000000, +1.0000000000000000,
1398-10001.000099999999, +0.0000000000000000,
1399+0.0000000000000000, -10001.000099999999,
1400+1.0000000000000000, +0.0000000000000000
1401call setResized(root, size(coef, 1, IK) - 1_IK)
1402[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1403F, T, F, F
1404call setPolyRoot(root, count, coef, eigen)
1405count
1406+3
1407root(1:count)
1408+0.0000000000000000, +10000.000000000000,
1409+0.0000000000000000, +1.0000000000000004,
1410+0.0000000000000000, +0.10000000000000255E-3
1411getPolyVal(coef, root(1:count))
1412+0.0000000000000000, -0.70715235779061913E-4,
1413+0.0000000000000000, +0.36375347178818629E-11,
1414+0.0000000000000000, -0.25535129566378600E-13
1415
1416
1417coef
1418+0.00000000000000000000000000000000000, +1.00000000000000000000000000000000000,
1419-10001.0000999999999999999999999999996, +0.00000000000000000000000000000000000,
1420+0.00000000000000000000000000000000000, -10001.0000999999999999999999999999996,
1421+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1422call setResized(root, size(coef, 1, IK) - 1_IK)
1423[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1424F, T, F, F
1425call setPolyRoot(root, count, coef, eigen)
1426count
1427+3
1428root(1:count)
1429+0.00000000000000000000000000000000000, +9999.99999999999999999999999999999842,
1430+0.00000000000000000000000000000000000, +0.999999999999999999999999999999999904,
1431+0.00000000000000000000000000000000000, +0.100000000000000000000000000000000008E-3
1432getPolyVal(coef, root(1:count))
1433+0.00000000000000000000000000000000000, +0.115351482477835407341207567853721561E-21,
1434+0.00000000000000000000000000000000000, -0.157752921744758488723815153277131397E-29,
1435+0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1436
1437
1438coef
1439+0.0000000000000000, +1.0000000000000000,
1440-10001.000099999999, +0.0000000000000000,
1441+0.0000000000000000, -10001.000099999999,
1442+1.0000000000000000, +0.0000000000000000
1443call setResized(root, size(coef, 1, IK) - 1_IK)
1444[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1445F, F, T, F
1446call setPolyRoot(root, count, coef, eigen)
1447count
1448+3
1449root(1:count)
1450+0.0000000000000000, +10000.000000000000,
1451+0.0000000000000000, +1.0000000000000004,
1452+0.0000000000000000, +0.10000000000000255E-3
1453getPolyVal(coef, root(1:count))
1454+0.0000000000000000, -0.70715235779061913E-4,
1455+0.0000000000000000, +0.36375347178818629E-11,
1456+0.0000000000000000, -0.25535129566378600E-13
1457
1458
1459coef
1460+0.00000000000000000000000000000000000, +1.00000000000000000000000000000000000,
1461-10001.0000999999999999999999999999996, +0.00000000000000000000000000000000000,
1462+0.00000000000000000000000000000000000, -10001.0000999999999999999999999999996,
1463+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1464call setResized(root, size(coef, 1, IK) - 1_IK)
1465[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1466F, F, T, F
1467call setPolyRoot(root, count, coef, eigen)
1468count
1469+3
1470root(1:count)
1471+0.00000000000000000000000000000000000, +9999.99999999999999999999999999999842,
1472+0.00000000000000000000000000000000000, +0.999999999999999999999999999999999904,
1473+0.00000000000000000000000000000000000, +0.100000000000000000000000000000000008E-3
1474getPolyVal(coef, root(1:count))
1475+0.00000000000000000000000000000000000, +0.115351482477835407341207567853721561E-21,
1476+0.00000000000000000000000000000000000, -0.157752921744758488723815153277131397E-29,
1477+0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1478
1479
1480coef
1481+0.0000000000000000, +1.0000000000000000,
1482-10001.000099999999, +0.0000000000000000,
1483+0.0000000000000000, -10001.000099999999,
1484+1.0000000000000000, +0.0000000000000000
1485call setResized(root, size(coef, 1, IK) - 1_IK)
1486[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1487F, F, F, T
1488call setPolyRoot(root, count, coef, eigen)
1489count
1490+3
1491root(1:count)
1492+0.0000000000000000, +10000.000000000000,
1493+0.0000000000000000, +1.0000000000000004,
1494+0.0000000000000000, +0.10000000000000255E-3
1495getPolyVal(coef, root(1:count))
1496+0.0000000000000000, -0.70715235779061913E-4,
1497+0.0000000000000000, +0.36375347178818629E-11,
1498+0.0000000000000000, -0.25535129566378600E-13
1499
1500
1501coef
1502+0.00000000000000000000000000000000000, +1.00000000000000000000000000000000000,
1503-10001.0000999999999999999999999999996, +0.00000000000000000000000000000000000,
1504+0.00000000000000000000000000000000000, -10001.0000999999999999999999999999996,
1505+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1506call setResized(root, size(coef, 1, IK) - 1_IK)
1507[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1508F, F, F, T
1509call setPolyRoot(root, count, coef, eigen)
1510count
1511+3
1512root(1:count)
1513+0.00000000000000000000000000000000000, +9999.99999999999999999999999999999842,
1514+0.00000000000000000000000000000000000, +0.999999999999999999999999999999999904,
1515+0.00000000000000000000000000000000000, +0.100000000000000000000000000000000008E-3
1516getPolyVal(coef, root(1:count))
1517+0.00000000000000000000000000000000000, +0.115351482477835407341207567853721561E-21,
1518+0.00000000000000000000000000000000000, -0.157752921744758488723815153277131397E-29,
1519+0.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1520
1521
1522!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1523! Compute the roots of polynomials with complex coefficients with zeros at 1+i,1/2*(1+i)....1/(2**-9)*(1+i).
1524!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1525
1526
1527coef
1528+0.0000000000000000, +0.90949470177292824E-12,
1529-0.46520653995685279E-9, -0.46520653995685279E-9,
1530+0.15848036127863449E-6, +0.0000000000000000,
1531-0.11546426321729090E-4, +0.11546426321729090E-4,
1532+0.0000000000000000, -0.78207794285845011E-3,
1533+0.12715073651634160E-1, +0.12715073651634160E-1,
1534-0.20021195337176320, +0.0000000000000000,
1535+0.75670659542083740, -0.75670659542083740,
1536+0.0000000000000000, +2.6588592529296879,
1537-1.9980468750000000, -1.9980468750000000,
1538+1.0000000000000000, +0.0000000000000000
1539call setResized(root, size(coef, 1, IK) - 1_IK)
1540[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1541T, F, F, F
1542call setPolyRoot(root, count, coef, eigen)
1543count
1544+10
1545root(1:count)
1546+0.99999999999999845, +0.99999999999999911,
1547+0.50000000000000133, +0.50000000000000067,
1548+0.25000000000000017, +0.25000000000000028,
1549+0.12499999999999911, +0.12499999999999924,
1550+0.62500000000001193E-1, +0.62500000000001124E-1,
1551+0.31249999999999212E-1, +0.31249999999999153E-1,
1552+0.15625000000000406E-1, +0.15625000000000503E-1,
1553+0.78124999999998820E-2, +0.78124999999998473E-2,
1554+0.39062500000000139E-2, +0.39062500000000173E-2,
1555+0.19531249999999998E-2, +0.19531250000000004E-2
1556getPolyVal(coef, root(1:count))
1557-0.30312292689246898E-14, -0.39170764430220062E-14,
1558-0.68538197226804901E-17, +0.80868759391036751E-17,
1559-0.17941598983115063E-19, +0.37617071523821058E-19,
1560-0.96831376073107395E-22, +0.76998478904539376E-22,
1561+0.18929632499428235E-23, +0.45584800724739300E-23,
1562+0.76689901761965884E-25, +0.68298946085311025E-24,
1563-0.20598735957131060E-25, +0.72903369416905027E-25,
1564-0.16155871338926322E-26, +0.24233807008389483E-26,
1565+0.0000000000000000, -0.80779356694631609E-27,
1566+0.0000000000000000, -0.20194839173657902E-27
1567
1568
1569coef
1570+0.00000000000000000000000000000000000, +0.909494701772928199999999999999999977E-12,
1571-0.465206539956852800000000000000000002E-9, -0.465206539956852800000000000000000002E-9,
1572+0.158480361278634500000000000000000004E-6, +0.00000000000000000000000000000000000,
1573-0.115464263217290900000000000000000001E-4, +0.115464263217290900000000000000000001E-4,
1574+0.00000000000000000000000000000000000, -0.782077942858450099999999999999999970E-3,
1575+0.127150736516341599999999999999999998E-1, +0.127150736516341599999999999999999998E-1,
1576-0.200211953371763200000000000000000000, +0.00000000000000000000000000000000000,
1577+0.756706595420837399999999999999999953, -0.756706595420837399999999999999999953,
1578+0.00000000000000000000000000000000000, +2.65885925292968799999999999999999995,
1579-1.99804687500000000000000000000000000, -1.99804687500000000000000000000000000,
1580+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1581call setResized(root, size(coef, 1, IK) - 1_IK)
1582[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1583T, F, F, F
1584call setPolyRoot(root, count, coef, eigen)
1585count
1586+10
1587root(1:count)
1588+0.999999999999999160184470589450448173, +0.999999999999999160184470589450448944,
1589+0.500000000000001492398035863052857764, +0.500000000000001492398035863052858149,
1590+0.249999999999999617367224612848345132, +0.249999999999999617367224612848344434,
1591+0.124999999999999149032692721659057207, +0.124999999999999149032692721659057592,
1592+0.625000000000009555071172310128834721E-1, +0.625000000000009555071172310128834842E-1,
1593+0.312499999999994379028135239093267093E-1, +0.312499999999994379028135239093266431E-1,
1594+0.156250000000002691698099555840415078E-1, +0.156250000000002691698099555840415649E-1,
1595+0.781249999999989766148737734007061361E-2, +0.781249999999989766148737734007058653E-2,
1596+0.390625000000002310324757362451072950E-2, +0.390625000000002310324757362451074380E-2,
1597+0.195312499999999767310055151845923676E-2, +0.195312499999999767310055151845923318E-2
1598getPolyVal(coef, root(1:count))
1599-0.330908113531804644550698914860698518E-32, +0.737655648425543017921748959548643300E-33,
1600+0.646304339719146005950884128119047103E-35, -0.199728685471399985252652738182225539E-34,
1601+0.612273361057752245328214721921763582E-37, -0.491287832226650747595597082681272950E-37,
1602+0.380437118781080261768012420837796041E-39, -0.701672705528289773730040710639353438E-39,
1603+0.223655993021642834626120514802966177E-41, -0.822711086520502132446014911659405323E-41,
1604-0.173323103806175811459878802833171501E-42, +0.819759601630017986490381806224600937E-43,
1605+0.516728808719776294903125283838156573E-44, +0.182168800362226219220084845827689097E-43,
1606-0.192678538844662347252012817702363468E-44, +0.262743462060903200798199296866859275E-45,
1607-0.437905770101505334663665494778098791E-45, -0.175162308040602133865466197911239516E-45,
1608-0.218952885050752667331832747389049396E-45, -0.350324616081204267730932395822479033E-45
1609
1610
1611coef
1612+0.0000000000000000, +0.90949470177292824E-12,
1613-0.46520653995685279E-9, -0.46520653995685279E-9,
1614+0.15848036127863449E-6, +0.0000000000000000,
1615-0.11546426321729090E-4, +0.11546426321729090E-4,
1616+0.0000000000000000, -0.78207794285845011E-3,
1617+0.12715073651634160E-1, +0.12715073651634160E-1,
1618-0.20021195337176320, +0.0000000000000000,
1619+0.75670659542083740, -0.75670659542083740,
1620+0.0000000000000000, +2.6588592529296879,
1621-1.9980468750000000, -1.9980468750000000,
1622+1.0000000000000000, +0.0000000000000000
1623call setResized(root, size(coef, 1, IK) - 1_IK)
1624[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1625F, T, F, F
1626call setPolyRoot(root, count, coef, eigen)
1627count
1628+10
1629root(1:count)
1630+0.99999999999999845, +0.99999999999999911,
1631+0.50000000000000133, +0.50000000000000067,
1632+0.25000000000000017, +0.25000000000000028,
1633+0.12499999999999911, +0.12499999999999924,
1634+0.62500000000001193E-1, +0.62500000000001124E-1,
1635+0.31249999999999212E-1, +0.31249999999999153E-1,
1636+0.15625000000000406E-1, +0.15625000000000503E-1,
1637+0.78124999999998820E-2, +0.78124999999998473E-2,
1638+0.39062500000000139E-2, +0.39062500000000173E-2,
1639+0.19531249999999998E-2, +0.19531250000000004E-2
1640getPolyVal(coef, root(1:count))
1641-0.30312292689246898E-14, -0.39170764430220062E-14,
1642-0.68538197226804901E-17, +0.80868759391036751E-17,
1643-0.17941598983115063E-19, +0.37617071523821058E-19,
1644-0.96831376073107395E-22, +0.76998478904539376E-22,
1645+0.18929632499428235E-23, +0.45584800724739300E-23,
1646+0.76689901761965884E-25, +0.68298946085311025E-24,
1647-0.20598735957131060E-25, +0.72903369416905027E-25,
1648-0.16155871338926322E-26, +0.24233807008389483E-26,
1649+0.0000000000000000, -0.80779356694631609E-27,
1650+0.0000000000000000, -0.20194839173657902E-27
1651
1652
1653coef
1654+0.00000000000000000000000000000000000, +0.909494701772928199999999999999999977E-12,
1655-0.465206539956852800000000000000000002E-9, -0.465206539956852800000000000000000002E-9,
1656+0.158480361278634500000000000000000004E-6, +0.00000000000000000000000000000000000,
1657-0.115464263217290900000000000000000001E-4, +0.115464263217290900000000000000000001E-4,
1658+0.00000000000000000000000000000000000, -0.782077942858450099999999999999999970E-3,
1659+0.127150736516341599999999999999999998E-1, +0.127150736516341599999999999999999998E-1,
1660-0.200211953371763200000000000000000000, +0.00000000000000000000000000000000000,
1661+0.756706595420837399999999999999999953, -0.756706595420837399999999999999999953,
1662+0.00000000000000000000000000000000000, +2.65885925292968799999999999999999995,
1663-1.99804687500000000000000000000000000, -1.99804687500000000000000000000000000,
1664+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1665call setResized(root, size(coef, 1, IK) - 1_IK)
1666[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1667F, T, F, F
1668call setPolyRoot(root, count, coef, eigen)
1669count
1670+10
1671root(1:count)
1672+0.999999999999999160184470589450448173, +0.999999999999999160184470589450448944,
1673+0.500000000000001492398035863052857764, +0.500000000000001492398035863052858149,
1674+0.249999999999999617367224612848345132, +0.249999999999999617367224612848344434,
1675+0.124999999999999149032692721659057207, +0.124999999999999149032692721659057592,
1676+0.625000000000009555071172310128834721E-1, +0.625000000000009555071172310128834842E-1,
1677+0.312499999999994379028135239093267093E-1, +0.312499999999994379028135239093266431E-1,
1678+0.156250000000002691698099555840415078E-1, +0.156250000000002691698099555840415649E-1,
1679+0.781249999999989766148737734007061361E-2, +0.781249999999989766148737734007058653E-2,
1680+0.390625000000002310324757362451072950E-2, +0.390625000000002310324757362451074380E-2,
1681+0.195312499999999767310055151845923676E-2, +0.195312499999999767310055151845923318E-2
1682getPolyVal(coef, root(1:count))
1683-0.330908113531804644550698914860698518E-32, +0.737655648425543017921748959548643300E-33,
1684+0.646304339719146005950884128119047103E-35, -0.199728685471399985252652738182225539E-34,
1685+0.612273361057752245328214721921763582E-37, -0.491287832226650747595597082681272950E-37,
1686+0.380437118781080261768012420837796041E-39, -0.701672705528289773730040710639353438E-39,
1687+0.223655993021642834626120514802966177E-41, -0.822711086520502132446014911659405323E-41,
1688-0.173323103806175811459878802833171501E-42, +0.819759601630017986490381806224600937E-43,
1689+0.516728808719776294903125283838156573E-44, +0.182168800362226219220084845827689097E-43,
1690-0.192678538844662347252012817702363468E-44, +0.262743462060903200798199296866859275E-45,
1691-0.437905770101505334663665494778098791E-45, -0.175162308040602133865466197911239516E-45,
1692-0.218952885050752667331832747389049396E-45, -0.350324616081204267730932395822479033E-45
1693
1694
1695coef
1696+0.0000000000000000, +0.90949470177292824E-12,
1697-0.46520653995685279E-9, -0.46520653995685279E-9,
1698+0.15848036127863449E-6, +0.0000000000000000,
1699-0.11546426321729090E-4, +0.11546426321729090E-4,
1700+0.0000000000000000, -0.78207794285845011E-3,
1701+0.12715073651634160E-1, +0.12715073651634160E-1,
1702-0.20021195337176320, +0.0000000000000000,
1703+0.75670659542083740, -0.75670659542083740,
1704+0.0000000000000000, +2.6588592529296879,
1705-1.9980468750000000, -1.9980468750000000,
1706+1.0000000000000000, +0.0000000000000000
1707call setResized(root, size(coef, 1, IK) - 1_IK)
1708[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1709F, F, T, F
1710call setPolyRoot(root, count, coef, eigen)
1711count
1712+10
1713root(1:count)
1714+0.99999999999999845, +0.99999999999999911,
1715+0.50000000000000133, +0.50000000000000067,
1716+0.25000000000000017, +0.25000000000000028,
1717+0.12499999999999911, +0.12499999999999924,
1718+0.62500000000001193E-1, +0.62500000000001124E-1,
1719+0.31249999999999212E-1, +0.31249999999999153E-1,
1720+0.15625000000000406E-1, +0.15625000000000503E-1,
1721+0.78124999999998820E-2, +0.78124999999998473E-2,
1722+0.39062500000000139E-2, +0.39062500000000173E-2,
1723+0.19531249999999998E-2, +0.19531250000000004E-2
1724getPolyVal(coef, root(1:count))
1725-0.30312292689246898E-14, -0.39170764430220062E-14,
1726-0.68538197226804901E-17, +0.80868759391036751E-17,
1727-0.17941598983115063E-19, +0.37617071523821058E-19,
1728-0.96831376073107395E-22, +0.76998478904539376E-22,
1729+0.18929632499428235E-23, +0.45584800724739300E-23,
1730+0.76689901761965884E-25, +0.68298946085311025E-24,
1731-0.20598735957131060E-25, +0.72903369416905027E-25,
1732-0.16155871338926322E-26, +0.24233807008389483E-26,
1733+0.0000000000000000, -0.80779356694631609E-27,
1734+0.0000000000000000, -0.20194839173657902E-27
1735
1736
1737coef
1738+0.00000000000000000000000000000000000, +0.909494701772928199999999999999999977E-12,
1739-0.465206539956852800000000000000000002E-9, -0.465206539956852800000000000000000002E-9,
1740+0.158480361278634500000000000000000004E-6, +0.00000000000000000000000000000000000,
1741-0.115464263217290900000000000000000001E-4, +0.115464263217290900000000000000000001E-4,
1742+0.00000000000000000000000000000000000, -0.782077942858450099999999999999999970E-3,
1743+0.127150736516341599999999999999999998E-1, +0.127150736516341599999999999999999998E-1,
1744-0.200211953371763200000000000000000000, +0.00000000000000000000000000000000000,
1745+0.756706595420837399999999999999999953, -0.756706595420837399999999999999999953,
1746+0.00000000000000000000000000000000000, +2.65885925292968799999999999999999995,
1747-1.99804687500000000000000000000000000, -1.99804687500000000000000000000000000,
1748+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1749call setResized(root, size(coef, 1, IK) - 1_IK)
1750[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1751F, F, T, F
1752call setPolyRoot(root, count, coef, eigen)
1753count
1754+10
1755root(1:count)
1756+0.999999999999999160184470589450448173, +0.999999999999999160184470589450448944,
1757+0.500000000000001492398035863052857764, +0.500000000000001492398035863052858149,
1758+0.249999999999999617367224612848345132, +0.249999999999999617367224612848344434,
1759+0.124999999999999149032692721659057207, +0.124999999999999149032692721659057592,
1760+0.625000000000009555071172310128834721E-1, +0.625000000000009555071172310128834842E-1,
1761+0.312499999999994379028135239093267093E-1, +0.312499999999994379028135239093266431E-1,
1762+0.156250000000002691698099555840415078E-1, +0.156250000000002691698099555840415649E-1,
1763+0.781249999999989766148737734007061361E-2, +0.781249999999989766148737734007058653E-2,
1764+0.390625000000002310324757362451072950E-2, +0.390625000000002310324757362451074380E-2,
1765+0.195312499999999767310055151845923676E-2, +0.195312499999999767310055151845923318E-2
1766getPolyVal(coef, root(1:count))
1767-0.330908113531804644550698914860698518E-32, +0.737655648425543017921748959548643300E-33,
1768+0.646304339719146005950884128119047103E-35, -0.199728685471399985252652738182225539E-34,
1769+0.612273361057752245328214721921763582E-37, -0.491287832226650747595597082681272950E-37,
1770+0.380437118781080261768012420837796041E-39, -0.701672705528289773730040710639353438E-39,
1771+0.223655993021642834626120514802966177E-41, -0.822711086520502132446014911659405323E-41,
1772-0.173323103806175811459878802833171501E-42, +0.819759601630017986490381806224600937E-43,
1773+0.516728808719776294903125283838156573E-44, +0.182168800362226219220084845827689097E-43,
1774-0.192678538844662347252012817702363468E-44, +0.262743462060903200798199296866859275E-45,
1775-0.437905770101505334663665494778098791E-45, -0.175162308040602133865466197911239516E-45,
1776-0.218952885050752667331832747389049396E-45, -0.350324616081204267730932395822479033E-45
1777
1778
1779coef
1780+0.0000000000000000, +0.90949470177292824E-12,
1781-0.46520653995685279E-9, -0.46520653995685279E-9,
1782+0.15848036127863449E-6, +0.0000000000000000,
1783-0.11546426321729090E-4, +0.11546426321729090E-4,
1784+0.0000000000000000, -0.78207794285845011E-3,
1785+0.12715073651634160E-1, +0.12715073651634160E-1,
1786-0.20021195337176320, +0.0000000000000000,
1787+0.75670659542083740, -0.75670659542083740,
1788+0.0000000000000000, +2.6588592529296879,
1789-1.9980468750000000, -1.9980468750000000,
1790+1.0000000000000000, +0.0000000000000000
1791call setResized(root, size(coef, 1, IK) - 1_IK)
1792[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1793F, F, F, T
1794call setPolyRoot(root, count, coef, eigen)
1795count
1796+10
1797root(1:count)
1798+0.99999999999999845, +0.99999999999999911,
1799+0.50000000000000133, +0.50000000000000067,
1800+0.25000000000000017, +0.25000000000000028,
1801+0.12499999999999911, +0.12499999999999924,
1802+0.62500000000001193E-1, +0.62500000000001124E-1,
1803+0.31249999999999212E-1, +0.31249999999999153E-1,
1804+0.15625000000000406E-1, +0.15625000000000503E-1,
1805+0.78124999999998820E-2, +0.78124999999998473E-2,
1806+0.39062500000000139E-2, +0.39062500000000173E-2,
1807+0.19531249999999998E-2, +0.19531250000000004E-2
1808getPolyVal(coef, root(1:count))
1809-0.30312292689246898E-14, -0.39170764430220062E-14,
1810-0.68538197226804901E-17, +0.80868759391036751E-17,
1811-0.17941598983115063E-19, +0.37617071523821058E-19,
1812-0.96831376073107395E-22, +0.76998478904539376E-22,
1813+0.18929632499428235E-23, +0.45584800724739300E-23,
1814+0.76689901761965884E-25, +0.68298946085311025E-24,
1815-0.20598735957131060E-25, +0.72903369416905027E-25,
1816-0.16155871338926322E-26, +0.24233807008389483E-26,
1817+0.0000000000000000, -0.80779356694631609E-27,
1818+0.0000000000000000, -0.20194839173657902E-27
1819
1820
1821coef
1822+0.00000000000000000000000000000000000, +0.909494701772928199999999999999999977E-12,
1823-0.465206539956852800000000000000000002E-9, -0.465206539956852800000000000000000002E-9,
1824+0.158480361278634500000000000000000004E-6, +0.00000000000000000000000000000000000,
1825-0.115464263217290900000000000000000001E-4, +0.115464263217290900000000000000000001E-4,
1826+0.00000000000000000000000000000000000, -0.782077942858450099999999999999999970E-3,
1827+0.127150736516341599999999999999999998E-1, +0.127150736516341599999999999999999998E-1,
1828-0.200211953371763200000000000000000000, +0.00000000000000000000000000000000000,
1829+0.756706595420837399999999999999999953, -0.756706595420837399999999999999999953,
1830+0.00000000000000000000000000000000000, +2.65885925292968799999999999999999995,
1831-1.99804687500000000000000000000000000, -1.99804687500000000000000000000000000,
1832+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1833call setResized(root, size(coef, 1, IK) - 1_IK)
1834[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1835F, F, F, T
1836call setPolyRoot(root, count, coef, eigen)
1837count
1838+10
1839root(1:count)
1840+0.999999999999999160184470589450448173, +0.999999999999999160184470589450448944,
1841+0.500000000000001492398035863052857764, +0.500000000000001492398035863052858149,
1842+0.249999999999999617367224612848345132, +0.249999999999999617367224612848344434,
1843+0.124999999999999149032692721659057207, +0.124999999999999149032692721659057592,
1844+0.625000000000009555071172310128834721E-1, +0.625000000000009555071172310128834842E-1,
1845+0.312499999999994379028135239093267093E-1, +0.312499999999994379028135239093266431E-1,
1846+0.156250000000002691698099555840415078E-1, +0.156250000000002691698099555840415649E-1,
1847+0.781249999999989766148737734007061361E-2, +0.781249999999989766148737734007058653E-2,
1848+0.390625000000002310324757362451072950E-2, +0.390625000000002310324757362451074380E-2,
1849+0.195312499999999767310055151845923676E-2, +0.195312499999999767310055151845923318E-2
1850getPolyVal(coef, root(1:count))
1851-0.330908113531804644550698914860698518E-32, +0.737655648425543017921748959548643300E-33,
1852+0.646304339719146005950884128119047103E-35, -0.199728685471399985252652738182225539E-34,
1853+0.612273361057752245328214721921763582E-37, -0.491287832226650747595597082681272950E-37,
1854+0.380437118781080261768012420837796041E-39, -0.701672705528289773730040710639353438E-39,
1855+0.223655993021642834626120514802966177E-41, -0.822711086520502132446014911659405323E-41,
1856-0.173323103806175811459878802833171501E-42, +0.819759601630017986490381806224600937E-43,
1857+0.516728808719776294903125283838156573E-44, +0.182168800362226219220084845827689097E-43,
1858-0.192678538844662347252012817702363468E-44, +0.262743462060903200798199296866859275E-45,
1859-0.437905770101505334663665494778098791E-45, -0.175162308040602133865466197911239516E-45,
1860-0.218952885050752667331832747389049396E-45, -0.350324616081204267730932395822479033E-45
1861
1862
1863!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1864! Compute the roots of polynomials with complex coefficients with multiple zeros.
1865!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
1866
1867
1868coef
1869+288.000000, +0.00000000,
1870-1344.00000, +504.000000,
1871+2204.00000, -2352.00000,
1872-920.000000, +4334.00000,
1873-1587.00000, -3836.00000,
1874+2374.00000, +1394.00000,
1875-1293.00000, +200.000000,
1876+284.000000, -334.000000,
1877+3.00000000, +100.000000,
1878-10.0000000, -10.0000000,
1879+1.00000000, +0.00000000
1880call setResized(root, size(coef, 1, IK) - 1_IK)
1881[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1882T, F, F, F
1883call setPolyRoot(root, count, coef, eigen)
1884count
1885+10
1886root(1:count)
1887-0.262260437E-5, +4.00000191,
1888+2.99939489, +0.243153726E-2,
1889+3.00061989, -0.242062425E-2,
1890+0.158268567E-1, +2.02321959,
1891+0.118745584E-1, +1.97478998,
1892-0.277059320E-1, +2.00198984,
1893+1.02006865, +0.411952510E-1,
1894+1.04016447, -0.220653433E-1,
1895+0.960722089, +0.191663913E-1,
1896+0.979039192, -0.383066721E-1
1897getPolyVal(coef, root(1:count))
1898+0.239379883, -0.129583254,
1899+0.220031738E-1, +0.146927238E-1,
1900-0.135498047E-1, +0.105561465E-1,
1901-0.311279297E-2, +0.171809196E-1,
1902-0.695800781E-2, +0.117588043E-1,
1903-0.726318359E-2, +0.152904987E-1,
1904+0.823974609E-3, +0.151634216E-3,
1905+0.732421875E-3, -0.166893005E-3,
1906+0.823974609E-3, -0.217437744E-3,
1907+0.457763672E-3, -0.325202942E-3
1908
1909
1910coef
1911+288.00000000000000, +0.0000000000000000,
1912-1344.0000000000000, +504.00000000000000,
1913+2204.0000000000000, -2352.0000000000000,
1914-920.00000000000000, +4334.0000000000000,
1915-1587.0000000000000, -3836.0000000000000,
1916+2374.0000000000000, +1394.0000000000000,
1917-1293.0000000000000, +200.00000000000000,
1918+284.00000000000000, -334.00000000000000,
1919+3.0000000000000000, +100.00000000000000,
1920-10.000000000000000, -10.000000000000000,
1921+1.0000000000000000, +0.0000000000000000
1922call setResized(root, size(coef, 1, IK) - 1_IK)
1923[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1924T, F, F, F
1925call setPolyRoot(root, count, coef, eigen)
1926count
1927+10
1928root(1:count)
1929-0.26645352591003757E-13, +3.9999999999999880,
1930+3.0000001970524699, -0.23536775645374987E-6,
1931+2.9999998029474919, +0.23536782983636444E-6,
1932+0.10185201113391936E-4, +1.9999738276389909,
1933+0.17573524658964788E-4, +2.0000219075497694,
1934-0.27758725751883115E-4, +2.0000042648112437,
1935+0.99972283047521127, +0.13862002582648678E-4,
1936+1.0000137952404726, +0.27729146568424598E-3,
1937+0.99998601603900350, -0.27723617160111893E-3,
1938+1.0002773582453568, -0.13917296733077833E-4
1939getPolyVal(coef, root(1:count))
1940+0.33077185435104184E-9, +0.20417161294972133E-8,
1941-0.56900262279668823E-10, +0.24780200131034645E-9,
1942-0.16075318853836507E-9, +0.27178263366041855E-9,
1943+0.40927261579781771E-11, +0.18487610964693091E-10,
1944-0.34674485505092889E-11, +0.80048992608106051E-11,
1945-0.26147972675971687E-11, +0.25204519894794775E-10,
1946+0.22737367544323206E-12, +0.10120151244796816E-11,
1947+0.11368683772161603E-12, +0.10641210135275969E-11,
1948+0.56843418860808015E-13, +0.13136297605242930E-11,
1949+0.0000000000000000, +0.14300774106579262E-11
1950
1951
1952coef
1953+288.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
1954-1344.00000000000000000000000000000000, +504.000000000000000000000000000000000,
1955+2204.00000000000000000000000000000000, -2352.00000000000000000000000000000000,
1956-920.000000000000000000000000000000000, +4334.00000000000000000000000000000000,
1957-1587.00000000000000000000000000000000, -3836.00000000000000000000000000000000,
1958+2374.00000000000000000000000000000000, +1394.00000000000000000000000000000000,
1959-1293.00000000000000000000000000000000, +200.000000000000000000000000000000000,
1960+284.000000000000000000000000000000000, -334.000000000000000000000000000000000,
1961+3.00000000000000000000000000000000000, +100.000000000000000000000000000000000,
1962-10.0000000000000000000000000000000000, -10.0000000000000000000000000000000000,
1963+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
1964call setResized(root, size(coef, 1, IK) - 1_IK)
1965[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
1966T, F, F, F
1967call setPolyRoot(root, count, coef, eigen)
1968count
1969+10
1970root(1:count)
1971-0.130963236218332038007806500095775058E-31, +4.00000000000000000000000000000001233,
1972+3.00000000000000017551097726216032856, -0.110201355633942977982250385201797701E-15,
1973+2.99999999999999982448902273783963986, +0.110201355633943002360704498217562890E-15,
1974+0.198827846113882935119497667613680559E-10, +2.00000000001021969660975542649721576,
1975-0.109087542230478321562619250537222123E-11, +1.99999999997767115512427343820588314,
1976-0.187919091890835102963115145452168761E-10, +2.00000000001210914826597113529687375,
1977+0.999999998924471798982144453844539050, +0.569327565931999073274615515126895450E-8,
1978+1.00000000569327572067379369961664497, +0.107552815246768798396814854480103414E-8,
1979+0.999999994306724389230175509482966430, -0.107552813966405382053522281260010247E-8,
1980+1.00000000107552809111388633705588402, -0.569327567212362489617908738729673540E-8
1981getPolyVal(coef, root(1:count))
1982+0.119226465062840671740415126035427104E-26, -0.104092661634241323385969495840791379E-28,
1983-0.109996792471754833617097901821618505E-27, +0.130434128372842219928401259706545043E-28,
1984-0.143769899976529401536287531022787790E-27, +0.135376768311312987970879984352679944E-27,
1985+0.833234331139693719466138297079942955E-29, +0.739591563885907217517079181128459199E-29,
1986+0.493038065763132378382330353301741394E-29, +0.103976104123069846169611920461958392E-28,
1987+0.576854536942864882707326513363037430E-29, +0.541027064395165263276723173580121787E-29,
1988-0.345126646034192664867631247311218975E-30, +0.283326920330550838279326406730858078E-30,
1989-0.295822839457879427029398211981044836E-30, +0.781981766077889895393086715455354831E-32,
1990+0.147911419728939713514699105990522418E-30, -0.297212059298750093875342660053652258E-30,
1991-0.542341872339445616220563388631915533E-30, +0.206541271182968673360478096961938272E-30
1992
1993
1994coef
1995+288.000000, +0.00000000,
1996-1344.00000, +504.000000,
1997+2204.00000, -2352.00000,
1998-920.000000, +4334.00000,
1999-1587.00000, -3836.00000,
2000+2374.00000, +1394.00000,
2001-1293.00000, +200.000000,
2002+284.000000, -334.000000,
2003+3.00000000, +100.000000,
2004-10.0000000, -10.0000000,
2005+1.00000000, +0.00000000
2006call setResized(root, size(coef, 1, IK) - 1_IK)
2007[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2008F, T, F, F
2009call setPolyRoot(root, count, coef, eigen)
2010count
2011+10
2012root(1:count)
2013-0.262260437E-5, +4.00000191,
2014+2.99939489, +0.243153726E-2,
2015+3.00061989, -0.242062425E-2,
2016+0.158268567E-1, +2.02321959,
2017+0.118745584E-1, +1.97478998,
2018-0.277059320E-1, +2.00198984,
2019+1.02006865, +0.411952510E-1,
2020+1.04016447, -0.220653433E-1,
2021+0.960722089, +0.191663913E-1,
2022+0.979039192, -0.383066721E-1
2023getPolyVal(coef, root(1:count))
2024+0.239379883, -0.129583254,
2025+0.220031738E-1, +0.146927238E-1,
2026-0.135498047E-1, +0.105561465E-1,
2027-0.311279297E-2, +0.171809196E-1,
2028-0.695800781E-2, +0.117588043E-1,
2029-0.726318359E-2, +0.152904987E-1,
2030+0.823974609E-3, +0.151634216E-3,
2031+0.732421875E-3, -0.166893005E-3,
2032+0.823974609E-3, -0.217437744E-3,
2033+0.457763672E-3, -0.325202942E-3
2034
2035
2036coef
2037+288.00000000000000, +0.0000000000000000,
2038-1344.0000000000000, +504.00000000000000,
2039+2204.0000000000000, -2352.0000000000000,
2040-920.00000000000000, +4334.0000000000000,
2041-1587.0000000000000, -3836.0000000000000,
2042+2374.0000000000000, +1394.0000000000000,
2043-1293.0000000000000, +200.00000000000000,
2044+284.00000000000000, -334.00000000000000,
2045+3.0000000000000000, +100.00000000000000,
2046-10.000000000000000, -10.000000000000000,
2047+1.0000000000000000, +0.0000000000000000
2048call setResized(root, size(coef, 1, IK) - 1_IK)
2049[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2050F, T, F, F
2051call setPolyRoot(root, count, coef, eigen)
2052count
2053+10
2054root(1:count)
2055-0.26645352591003757E-13, +3.9999999999999880,
2056+3.0000001970524699, -0.23536775645374987E-6,
2057+2.9999998029474919, +0.23536782983636444E-6,
2058+0.10185201113391936E-4, +1.9999738276389909,
2059+0.17573524658964788E-4, +2.0000219075497694,
2060-0.27758725751883115E-4, +2.0000042648112437,
2061+0.99972283047521127, +0.13862002582648678E-4,
2062+1.0000137952404726, +0.27729146568424598E-3,
2063+0.99998601603900350, -0.27723617160111893E-3,
2064+1.0002773582453568, -0.13917296733077833E-4
2065getPolyVal(coef, root(1:count))
2066+0.33077185435104184E-9, +0.20417161294972133E-8,
2067-0.56900262279668823E-10, +0.24780200131034645E-9,
2068-0.16075318853836507E-9, +0.27178263366041855E-9,
2069+0.40927261579781771E-11, +0.18487610964693091E-10,
2070-0.34674485505092889E-11, +0.80048992608106051E-11,
2071-0.26147972675971687E-11, +0.25204519894794775E-10,
2072+0.22737367544323206E-12, +0.10120151244796816E-11,
2073+0.11368683772161603E-12, +0.10641210135275969E-11,
2074+0.56843418860808015E-13, +0.13136297605242930E-11,
2075+0.0000000000000000, +0.14300774106579262E-11
2076
2077
2078coef
2079+288.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2080-1344.00000000000000000000000000000000, +504.000000000000000000000000000000000,
2081+2204.00000000000000000000000000000000, -2352.00000000000000000000000000000000,
2082-920.000000000000000000000000000000000, +4334.00000000000000000000000000000000,
2083-1587.00000000000000000000000000000000, -3836.00000000000000000000000000000000,
2084+2374.00000000000000000000000000000000, +1394.00000000000000000000000000000000,
2085-1293.00000000000000000000000000000000, +200.000000000000000000000000000000000,
2086+284.000000000000000000000000000000000, -334.000000000000000000000000000000000,
2087+3.00000000000000000000000000000000000, +100.000000000000000000000000000000000,
2088-10.0000000000000000000000000000000000, -10.0000000000000000000000000000000000,
2089+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2090call setResized(root, size(coef, 1, IK) - 1_IK)
2091[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2092F, T, F, F
2093call setPolyRoot(root, count, coef, eigen)
2094count
2095+10
2096root(1:count)
2097-0.130963236218332038007806500095775058E-31, +4.00000000000000000000000000000001233,
2098+3.00000000000000017551097726216032856, -0.110201355633942977982250385201797701E-15,
2099+2.99999999999999982448902273783963986, +0.110201355633943002360704498217562890E-15,
2100+0.198827846113882935119497667613680559E-10, +2.00000000001021969660975542649721576,
2101-0.109087542230478321562619250537222123E-11, +1.99999999997767115512427343820588314,
2102-0.187919091890835102963115145452168761E-10, +2.00000000001210914826597113529687375,
2103+0.999999998924471798982144453844539050, +0.569327565931999073274615515126895450E-8,
2104+1.00000000569327572067379369961664497, +0.107552815246768798396814854480103414E-8,
2105+0.999999994306724389230175509482966430, -0.107552813966405382053522281260010247E-8,
2106+1.00000000107552809111388633705588402, -0.569327567212362489617908738729673540E-8
2107getPolyVal(coef, root(1:count))
2108+0.119226465062840671740415126035427104E-26, -0.104092661634241323385969495840791379E-28,
2109-0.109996792471754833617097901821618505E-27, +0.130434128372842219928401259706545043E-28,
2110-0.143769899976529401536287531022787790E-27, +0.135376768311312987970879984352679944E-27,
2111+0.833234331139693719466138297079942955E-29, +0.739591563885907217517079181128459199E-29,
2112+0.493038065763132378382330353301741394E-29, +0.103976104123069846169611920461958392E-28,
2113+0.576854536942864882707326513363037430E-29, +0.541027064395165263276723173580121787E-29,
2114-0.345126646034192664867631247311218975E-30, +0.283326920330550838279326406730858078E-30,
2115-0.295822839457879427029398211981044836E-30, +0.781981766077889895393086715455354831E-32,
2116+0.147911419728939713514699105990522418E-30, -0.297212059298750093875342660053652258E-30,
2117-0.542341872339445616220563388631915533E-30, +0.206541271182968673360478096961938272E-30
2118
2119
2120coef
2121+288.000000, +0.00000000,
2122-1344.00000, +504.000000,
2123+2204.00000, -2352.00000,
2124-920.000000, +4334.00000,
2125-1587.00000, -3836.00000,
2126+2374.00000, +1394.00000,
2127-1293.00000, +200.000000,
2128+284.000000, -334.000000,
2129+3.00000000, +100.000000,
2130-10.0000000, -10.0000000,
2131+1.00000000, +0.00000000
2132call setResized(root, size(coef, 1, IK) - 1_IK)
2133[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2134F, F, T, F
2135call setPolyRoot(root, count, coef, eigen)
2136count
2137+10
2138root(1:count)
2139-0.262260437E-5, +4.00000191,
2140+2.99939489, +0.243153726E-2,
2141+3.00061989, -0.242062425E-2,
2142+0.158268567E-1, +2.02321959,
2143+0.118745584E-1, +1.97478998,
2144-0.277059320E-1, +2.00198984,
2145+1.02006865, +0.411952510E-1,
2146+1.04016447, -0.220653433E-1,
2147+0.960722089, +0.191663913E-1,
2148+0.979039192, -0.383066721E-1
2149getPolyVal(coef, root(1:count))
2150+0.239379883, -0.129583254,
2151+0.220031738E-1, +0.146927238E-1,
2152-0.135498047E-1, +0.105561465E-1,
2153-0.311279297E-2, +0.171809196E-1,
2154-0.695800781E-2, +0.117588043E-1,
2155-0.726318359E-2, +0.152904987E-1,
2156+0.823974609E-3, +0.151634216E-3,
2157+0.732421875E-3, -0.166893005E-3,
2158+0.823974609E-3, -0.217437744E-3,
2159+0.457763672E-3, -0.325202942E-3
2160
2161
2162coef
2163+288.00000000000000, +0.0000000000000000,
2164-1344.0000000000000, +504.00000000000000,
2165+2204.0000000000000, -2352.0000000000000,
2166-920.00000000000000, +4334.0000000000000,
2167-1587.0000000000000, -3836.0000000000000,
2168+2374.0000000000000, +1394.0000000000000,
2169-1293.0000000000000, +200.00000000000000,
2170+284.00000000000000, -334.00000000000000,
2171+3.0000000000000000, +100.00000000000000,
2172-10.000000000000000, -10.000000000000000,
2173+1.0000000000000000, +0.0000000000000000
2174call setResized(root, size(coef, 1, IK) - 1_IK)
2175[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2176F, F, T, F
2177call setPolyRoot(root, count, coef, eigen)
2178count
2179+10
2180root(1:count)
2181-0.26645352591003757E-13, +3.9999999999999880,
2182+3.0000001970524699, -0.23536775645374987E-6,
2183+2.9999998029474919, +0.23536782983636444E-6,
2184+0.10185201113391936E-4, +1.9999738276389909,
2185+0.17573524658964788E-4, +2.0000219075497694,
2186-0.27758725751883115E-4, +2.0000042648112437,
2187+0.99972283047521127, +0.13862002582648678E-4,
2188+1.0000137952404726, +0.27729146568424598E-3,
2189+0.99998601603900350, -0.27723617160111893E-3,
2190+1.0002773582453568, -0.13917296733077833E-4
2191getPolyVal(coef, root(1:count))
2192+0.33077185435104184E-9, +0.20417161294972133E-8,
2193-0.56900262279668823E-10, +0.24780200131034645E-9,
2194-0.16075318853836507E-9, +0.27178263366041855E-9,
2195+0.40927261579781771E-11, +0.18487610964693091E-10,
2196-0.34674485505092889E-11, +0.80048992608106051E-11,
2197-0.26147972675971687E-11, +0.25204519894794775E-10,
2198+0.22737367544323206E-12, +0.10120151244796816E-11,
2199+0.11368683772161603E-12, +0.10641210135275969E-11,
2200+0.56843418860808015E-13, +0.13136297605242930E-11,
2201+0.0000000000000000, +0.14300774106579262E-11
2202
2203
2204coef
2205+288.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2206-1344.00000000000000000000000000000000, +504.000000000000000000000000000000000,
2207+2204.00000000000000000000000000000000, -2352.00000000000000000000000000000000,
2208-920.000000000000000000000000000000000, +4334.00000000000000000000000000000000,
2209-1587.00000000000000000000000000000000, -3836.00000000000000000000000000000000,
2210+2374.00000000000000000000000000000000, +1394.00000000000000000000000000000000,
2211-1293.00000000000000000000000000000000, +200.000000000000000000000000000000000,
2212+284.000000000000000000000000000000000, -334.000000000000000000000000000000000,
2213+3.00000000000000000000000000000000000, +100.000000000000000000000000000000000,
2214-10.0000000000000000000000000000000000, -10.0000000000000000000000000000000000,
2215+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2216call setResized(root, size(coef, 1, IK) - 1_IK)
2217[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2218F, F, T, F
2219call setPolyRoot(root, count, coef, eigen)
2220count
2221+10
2222root(1:count)
2223-0.130963236218332038007806500095775058E-31, +4.00000000000000000000000000000001233,
2224+3.00000000000000017551097726216032856, -0.110201355633942977982250385201797701E-15,
2225+2.99999999999999982448902273783963986, +0.110201355633943002360704498217562890E-15,
2226+0.198827846113882935119497667613680559E-10, +2.00000000001021969660975542649721576,
2227-0.109087542230478321562619250537222123E-11, +1.99999999997767115512427343820588314,
2228-0.187919091890835102963115145452168761E-10, +2.00000000001210914826597113529687375,
2229+0.999999998924471798982144453844539050, +0.569327565931999073274615515126895450E-8,
2230+1.00000000569327572067379369961664497, +0.107552815246768798396814854480103414E-8,
2231+0.999999994306724389230175509482966430, -0.107552813966405382053522281260010247E-8,
2232+1.00000000107552809111388633705588402, -0.569327567212362489617908738729673540E-8
2233getPolyVal(coef, root(1:count))
2234+0.119226465062840671740415126035427104E-26, -0.104092661634241323385969495840791379E-28,
2235-0.109996792471754833617097901821618505E-27, +0.130434128372842219928401259706545043E-28,
2236-0.143769899976529401536287531022787790E-27, +0.135376768311312987970879984352679944E-27,
2237+0.833234331139693719466138297079942955E-29, +0.739591563885907217517079181128459199E-29,
2238+0.493038065763132378382330353301741394E-29, +0.103976104123069846169611920461958392E-28,
2239+0.576854536942864882707326513363037430E-29, +0.541027064395165263276723173580121787E-29,
2240-0.345126646034192664867631247311218975E-30, +0.283326920330550838279326406730858078E-30,
2241-0.295822839457879427029398211981044836E-30, +0.781981766077889895393086715455354831E-32,
2242+0.147911419728939713514699105990522418E-30, -0.297212059298750093875342660053652258E-30,
2243-0.542341872339445616220563388631915533E-30, +0.206541271182968673360478096961938272E-30
2244
2245
2246coef
2247+288.000000, +0.00000000,
2248-1344.00000, +504.000000,
2249+2204.00000, -2352.00000,
2250-920.000000, +4334.00000,
2251-1587.00000, -3836.00000,
2252+2374.00000, +1394.00000,
2253-1293.00000, +200.000000,
2254+284.000000, -334.000000,
2255+3.00000000, +100.000000,
2256-10.0000000, -10.0000000,
2257+1.00000000, +0.00000000
2258call setResized(root, size(coef, 1, IK) - 1_IK)
2259[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2260F, F, F, T
2261call setPolyRoot(root, count, coef, eigen)
2262count
2263+10
2264root(1:count)
2265-0.262260437E-5, +4.00000191,
2266+2.99939489, +0.243153726E-2,
2267+3.00061989, -0.242062425E-2,
2268+0.158268567E-1, +2.02321959,
2269+0.118745584E-1, +1.97478998,
2270-0.277059320E-1, +2.00198984,
2271+1.02006865, +0.411952510E-1,
2272+1.04016447, -0.220653433E-1,
2273+0.960722089, +0.191663913E-1,
2274+0.979039192, -0.383066721E-1
2275getPolyVal(coef, root(1:count))
2276+0.239379883, -0.129583254,
2277+0.220031738E-1, +0.146927238E-1,
2278-0.135498047E-1, +0.105561465E-1,
2279-0.311279297E-2, +0.171809196E-1,
2280-0.695800781E-2, +0.117588043E-1,
2281-0.726318359E-2, +0.152904987E-1,
2282+0.823974609E-3, +0.151634216E-3,
2283+0.732421875E-3, -0.166893005E-3,
2284+0.823974609E-3, -0.217437744E-3,
2285+0.457763672E-3, -0.325202942E-3
2286
2287
2288coef
2289+288.00000000000000, +0.0000000000000000,
2290-1344.0000000000000, +504.00000000000000,
2291+2204.0000000000000, -2352.0000000000000,
2292-920.00000000000000, +4334.0000000000000,
2293-1587.0000000000000, -3836.0000000000000,
2294+2374.0000000000000, +1394.0000000000000,
2295-1293.0000000000000, +200.00000000000000,
2296+284.00000000000000, -334.00000000000000,
2297+3.0000000000000000, +100.00000000000000,
2298-10.000000000000000, -10.000000000000000,
2299+1.0000000000000000, +0.0000000000000000
2300call setResized(root, size(coef, 1, IK) - 1_IK)
2301[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2302F, F, F, T
2303call setPolyRoot(root, count, coef, eigen)
2304count
2305+10
2306root(1:count)
2307-0.26645352591003757E-13, +3.9999999999999880,
2308+3.0000001970524699, -0.23536775645374987E-6,
2309+2.9999998029474919, +0.23536782983636444E-6,
2310+0.10185201113391936E-4, +1.9999738276389909,
2311+0.17573524658964788E-4, +2.0000219075497694,
2312-0.27758725751883115E-4, +2.0000042648112437,
2313+0.99972283047521127, +0.13862002582648678E-4,
2314+1.0000137952404726, +0.27729146568424598E-3,
2315+0.99998601603900350, -0.27723617160111893E-3,
2316+1.0002773582453568, -0.13917296733077833E-4
2317getPolyVal(coef, root(1:count))
2318+0.33077185435104184E-9, +0.20417161294972133E-8,
2319-0.56900262279668823E-10, +0.24780200131034645E-9,
2320-0.16075318853836507E-9, +0.27178263366041855E-9,
2321+0.40927261579781771E-11, +0.18487610964693091E-10,
2322-0.34674485505092889E-11, +0.80048992608106051E-11,
2323-0.26147972675971687E-11, +0.25204519894794775E-10,
2324+0.22737367544323206E-12, +0.10120151244796816E-11,
2325+0.11368683772161603E-12, +0.10641210135275969E-11,
2326+0.56843418860808015E-13, +0.13136297605242930E-11,
2327+0.0000000000000000, +0.14300774106579262E-11
2328
2329
2330coef
2331+288.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2332-1344.00000000000000000000000000000000, +504.000000000000000000000000000000000,
2333+2204.00000000000000000000000000000000, -2352.00000000000000000000000000000000,
2334-920.000000000000000000000000000000000, +4334.00000000000000000000000000000000,
2335-1587.00000000000000000000000000000000, -3836.00000000000000000000000000000000,
2336+2374.00000000000000000000000000000000, +1394.00000000000000000000000000000000,
2337-1293.00000000000000000000000000000000, +200.000000000000000000000000000000000,
2338+284.000000000000000000000000000000000, -334.000000000000000000000000000000000,
2339+3.00000000000000000000000000000000000, +100.000000000000000000000000000000000,
2340-10.0000000000000000000000000000000000, -10.0000000000000000000000000000000000,
2341+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2342call setResized(root, size(coef, 1, IK) - 1_IK)
2343[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2344F, F, F, T
2345call setPolyRoot(root, count, coef, eigen)
2346count
2347+10
2348root(1:count)
2349-0.130963236218332038007806500095775058E-31, +4.00000000000000000000000000000001233,
2350+3.00000000000000017551097726216032856, -0.110201355633942977982250385201797701E-15,
2351+2.99999999999999982448902273783963986, +0.110201355633943002360704498217562890E-15,
2352+0.198827846113882935119497667613680559E-10, +2.00000000001021969660975542649721576,
2353-0.109087542230478321562619250537222123E-11, +1.99999999997767115512427343820588314,
2354-0.187919091890835102963115145452168761E-10, +2.00000000001210914826597113529687375,
2355+0.999999998924471798982144453844539050, +0.569327565931999073274615515126895450E-8,
2356+1.00000000569327572067379369961664497, +0.107552815246768798396814854480103414E-8,
2357+0.999999994306724389230175509482966430, -0.107552813966405382053522281260010247E-8,
2358+1.00000000107552809111388633705588402, -0.569327567212362489617908738729673540E-8
2359getPolyVal(coef, root(1:count))
2360+0.119226465062840671740415126035427104E-26, -0.104092661634241323385969495840791379E-28,
2361-0.109996792471754833617097901821618505E-27, +0.130434128372842219928401259706545043E-28,
2362-0.143769899976529401536287531022787790E-27, +0.135376768311312987970879984352679944E-27,
2363+0.833234331139693719466138297079942955E-29, +0.739591563885907217517079181128459199E-29,
2364+0.493038065763132378382330353301741394E-29, +0.103976104123069846169611920461958392E-28,
2365+0.576854536942864882707326513363037430E-29, +0.541027064395165263276723173580121787E-29,
2366-0.345126646034192664867631247311218975E-30, +0.283326920330550838279326406730858078E-30,
2367-0.295822839457879427029398211981044836E-30, +0.781981766077889895393086715455354831E-32,
2368+0.147911419728939713514699105990522418E-30, -0.297212059298750093875342660053652258E-30,
2369-0.542341872339445616220563388631915533E-30, +0.206541271182968673360478096961938272E-30
2370
2371
2372!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
2373! Compute the roots of polynomials with complex coefficients with 12 zeros evenly distribute on a circle of radius 1. centered at 0+2i.
2374!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
2375
2376
2377coef
2378+4095.00000, +0.00000000,
2379+0.00000000, +24576.0000,
2380-67584.0000, +0.00000000,
2381+0.00000000, -112640.000,
2382+126720.000, +0.00000000,
2383+0.00000000, +101376.000,
2384-59136.0000, +0.00000000,
2385+0.00000000, -25344.0000,
2386+7920.00000, +0.00000000,
2387+0.00000000, +1760.00000,
2388-264.000000, +0.00000000,
2389+0.00000000, -24.0000000,
2390+1.00000000, +0.00000000
2391call setResized(root, size(coef, 1, IK) - 1_IK)
2392[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2393T, F, F, F
2394call setPolyRoot(root, count, coef, eigen)
2395count
2396+12
2397root(1:count)
2398-0.102758408E-2, +3.26374292,
2399+0.743275821, +2.94730639,
2400-0.743724287, +2.94551206,
2401+0.972983360, +2.28771806,
2402-0.971354008, +2.28610396,
2403+0.878654838, +1.98345017,
2404+0.860098600, +1.51398087,
2405-0.878169596, +1.98575449,
2406-0.860523164, +1.51400054,
2407+0.499328941, +1.13599277,
2408-0.566091039E-4, +1.00045466,
2409-0.499485791, +1.13598478
2410getPolyVal(coef, root(1:count))
2411+12.4841309, +0.153654099,
2412-2.42480469, -4.67864990,
2413-2.90429688, +5.80480957,
2414-1.59033203, -0.416015625,
2415-1.83007812, +0.395629883,
2416-0.713867188, -0.938720703E-1,
2417-0.152343750, +0.140258789,
2418-0.572753906, -0.150268555,
2419-0.998535156E-1, -0.616455078E-1,
2420-0.258789062E-1, -0.122070312E-2,
2421-0.170898438E-2, -0.675007701E-3,
2422-0.190429688E-1, -0.146484375E-1
2423
2424
2425coef
2426+4095.0000000000000, +0.0000000000000000,
2427+0.0000000000000000, +24576.000000000000,
2428-67584.000000000000, +0.0000000000000000,
2429+0.0000000000000000, -112640.00000000000,
2430+126720.00000000000, +0.0000000000000000,
2431+0.0000000000000000, +101376.00000000000,
2432-59136.000000000000, +0.0000000000000000,
2433+0.0000000000000000, -25344.000000000000,
2434+7920.0000000000000, +0.0000000000000000,
2435+0.0000000000000000, +1760.0000000000000,
2436-264.00000000000000, +0.0000000000000000,
2437+0.0000000000000000, -24.000000000000000,
2438+1.0000000000000000, +0.0000000000000000
2439call setResized(root, size(coef, 1, IK) - 1_IK)
2440[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2441T, F, F, F
2442call setPolyRoot(root, count, coef, eigen)
2443count
2444+12
2445root(1:count)
2446-0.22127855103803995E-10, +3.0000000012083348,
2447+0.50000000092178387, +2.8660254036044090,
2448+0.86602540366466041, +2.4999999995817723,
2449-0.50000000092225982, +2.8660254035707347,
2450-0.86602540364973568, +2.4999999995766795,
2451+0.99999999988689936, +2.0000000000036473,
2452-0.99999999988111377, +2.0000000000065561,
2453+0.86602540376976866, +1.5000000000087796,
2454-0.86602540376847770, +1.5000000000108240,
2455+0.49999999999651829, +1.1339745962147472,
2456+0.18475302723801401E-12, +0.99999999999813760,
2457-0.49999999999610956, +1.1339745962153789
2458getPolyVal(coef, root(1:count))
2459+0.14059878594707698E-7, +0.26553426475682450E-9,
2460+0.46070454118307680E-8, -0.11811152944574133E-7,
2461-0.32819116313476115E-8, -0.20859260985162109E-8,
2462+0.47079993237275630E-8, +0.13283624866744503E-7,
2463-0.23110260372050107E-8, +0.18424088921165094E-8,
2464-0.16898411558941007E-8, +0.26602720026858151E-10,
2465-0.92268237494863570E-9, -0.49340087571181357E-10,
2466-0.29012880986556411E-9, +0.29558577807620168E-10,
2467-0.10641088010743260E-9, -0.33196556614711881E-10,
2468-0.22737367544323206E-11, -0.93223206931725144E-11,
2469+0.19554136088117957E-10, +0.22170363269036277E-11,
2470-0.90949470177292824E-12, +0.60936145018786192E-10
2471
2472
2473coef
2474+4095.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2475+0.00000000000000000000000000000000000, +24576.0000000000000000000000000000000,
2476-67584.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2477+0.00000000000000000000000000000000000, -112640.000000000000000000000000000000,
2478+126720.000000000000000000000000000000, +0.00000000000000000000000000000000000,
2479+0.00000000000000000000000000000000000, +101376.000000000000000000000000000000,
2480-59136.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2481+0.00000000000000000000000000000000000, -25344.0000000000000000000000000000000,
2482+7920.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2483+0.00000000000000000000000000000000000, +1760.00000000000000000000000000000000,
2484-264.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2485+0.00000000000000000000000000000000000, -24.0000000000000000000000000000000000,
2486+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2487call setResized(root, size(coef, 1, IK) - 1_IK)
2488[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2489T, F, F, F
2490call setPolyRoot(root, count, coef, eigen)
2491count
2492+12
2493root(1:count)
2494+0.866025403784438646763723170731842991, +2.49999999999999999999999999930164047,
2495+0.500000000000000000000000001261300765, +2.86602540378443864676372317070946253,
2496-0.347698086029325849838930767012779505E-28, +3.00000000000000000000000000152269067,
2497-0.500000000000000000000000001265360529, +2.86602540378443864676372317065155482,
2498-0.866025403784438646763723170698404803, +2.49999999999999999999999999929392211,
2499+0.999999999999999999999999999757820376, +1.99999999999999999999999999995932648,
2500-0.999999999999999999999999999750830695, +1.99999999999999999999999999997135064,
2501+0.866025403784438646763723170716402811, +1.50000000000000000000000000003897716,
2502-0.866025403784438646763723170717795451, +1.50000000000000000000000000004211450,
2503+0.499999999999999999999999999996946149, +1.13397459621556135323627682925377416,
2504+0.400031557749517858232708991895941675E-31, +1.00000000000000000000000000000101670,
2505-0.499999999999999999999999999997192042, +1.13397459621556135323627682925417245
2506getPolyVal(coef, root(1:count))
2507-0.494852445845140705534777329001891802E-26, -0.688083924579027547270380241067910289E-26,
2508+0.716877347619594478167908333700731986E-26, -0.143695944266664931679530181469792529E-25,
2509+0.144759920412581771352079250372217687E-25, +0.417237703235191019806716927084944130E-27,
2510+0.751863328766146351737918495571023556E-26, +0.134045217167417378505074447134264243E-25,
2511-0.646037638330747618041935108538337783E-26, +0.660592122032075285851781500567805189E-26,
2512-0.272866987115947983491916910731315757E-26, -0.464639073175175953387508124951561089E-27,
2513-0.310732310566556550151679881864889496E-26, +0.336054745624151029105396368810466934E-27,
2514-0.737190515929035532157260344256763732E-27, +0.264268403249038954812929069369733387E-27,
2515-0.575474030358728112047855988373792555E-27, -0.318305375256678263483632476091604244E-27,
2516-0.686308987542280270708203851796024020E-28, -0.315544362088404722164691426113114492E-29,
2517-0.138050658413677065947052498924487590E-28, +0.480037869299421429879250790270093257E-30,
2518-0.958465999843529343575250206818585269E-28, -0.457539325028186847138802567864016013E-28
2519
2520
2521coef
2522+4095.00000, +0.00000000,
2523+0.00000000, +24576.0000,
2524-67584.0000, +0.00000000,
2525+0.00000000, -112640.000,
2526+126720.000, +0.00000000,
2527+0.00000000, +101376.000,
2528-59136.0000, +0.00000000,
2529+0.00000000, -25344.0000,
2530+7920.00000, +0.00000000,
2531+0.00000000, +1760.00000,
2532-264.000000, +0.00000000,
2533+0.00000000, -24.0000000,
2534+1.00000000, +0.00000000
2535call setResized(root, size(coef, 1, IK) - 1_IK)
2536[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2537F, T, F, F
2538call setPolyRoot(root, count, coef, eigen)
2539count
2540+12
2541root(1:count)
2542-0.102758408E-2, +3.26374292,
2543+0.743275821, +2.94730639,
2544-0.743724287, +2.94551206,
2545+0.972983360, +2.28771806,
2546-0.971354008, +2.28610396,
2547+0.878654838, +1.98345017,
2548+0.860098600, +1.51398087,
2549-0.878169596, +1.98575449,
2550-0.860523164, +1.51400054,
2551+0.499328941, +1.13599277,
2552-0.566091039E-4, +1.00045466,
2553-0.499485791, +1.13598478
2554getPolyVal(coef, root(1:count))
2555+12.4841309, +0.153654099,
2556-2.42480469, -4.67864990,
2557-2.90429688, +5.80480957,
2558-1.59033203, -0.416015625,
2559-1.83007812, +0.395629883,
2560-0.713867188, -0.938720703E-1,
2561-0.152343750, +0.140258789,
2562-0.572753906, -0.150268555,
2563-0.998535156E-1, -0.616455078E-1,
2564-0.258789062E-1, -0.122070312E-2,
2565-0.170898438E-2, -0.675007701E-3,
2566-0.190429688E-1, -0.146484375E-1
2567
2568
2569coef
2570+4095.0000000000000, +0.0000000000000000,
2571+0.0000000000000000, +24576.000000000000,
2572-67584.000000000000, +0.0000000000000000,
2573+0.0000000000000000, -112640.00000000000,
2574+126720.00000000000, +0.0000000000000000,
2575+0.0000000000000000, +101376.00000000000,
2576-59136.000000000000, +0.0000000000000000,
2577+0.0000000000000000, -25344.000000000000,
2578+7920.0000000000000, +0.0000000000000000,
2579+0.0000000000000000, +1760.0000000000000,
2580-264.00000000000000, +0.0000000000000000,
2581+0.0000000000000000, -24.000000000000000,
2582+1.0000000000000000, +0.0000000000000000
2583call setResized(root, size(coef, 1, IK) - 1_IK)
2584[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2585F, T, F, F
2586call setPolyRoot(root, count, coef, eigen)
2587count
2588+12
2589root(1:count)
2590-0.22127855103803995E-10, +3.0000000012083348,
2591+0.50000000092178387, +2.8660254036044090,
2592+0.86602540366466041, +2.4999999995817723,
2593-0.50000000092225982, +2.8660254035707347,
2594-0.86602540364973568, +2.4999999995766795,
2595+0.99999999988689936, +2.0000000000036473,
2596-0.99999999988111377, +2.0000000000065561,
2597+0.86602540376976866, +1.5000000000087796,
2598-0.86602540376847770, +1.5000000000108240,
2599+0.49999999999651829, +1.1339745962147472,
2600+0.18475302723801401E-12, +0.99999999999813760,
2601-0.49999999999610956, +1.1339745962153789
2602getPolyVal(coef, root(1:count))
2603+0.14059878594707698E-7, +0.26553426475682450E-9,
2604+0.46070454118307680E-8, -0.11811152944574133E-7,
2605-0.32819116313476115E-8, -0.20859260985162109E-8,
2606+0.47079993237275630E-8, +0.13283624866744503E-7,
2607-0.23110260372050107E-8, +0.18424088921165094E-8,
2608-0.16898411558941007E-8, +0.26602720026858151E-10,
2609-0.92268237494863570E-9, -0.49340087571181357E-10,
2610-0.29012880986556411E-9, +0.29558577807620168E-10,
2611-0.10641088010743260E-9, -0.33196556614711881E-10,
2612-0.22737367544323206E-11, -0.93223206931725144E-11,
2613+0.19554136088117957E-10, +0.22170363269036277E-11,
2614-0.90949470177292824E-12, +0.60936145018786192E-10
2615
2616
2617coef
2618+4095.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2619+0.00000000000000000000000000000000000, +24576.0000000000000000000000000000000,
2620-67584.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2621+0.00000000000000000000000000000000000, -112640.000000000000000000000000000000,
2622+126720.000000000000000000000000000000, +0.00000000000000000000000000000000000,
2623+0.00000000000000000000000000000000000, +101376.000000000000000000000000000000,
2624-59136.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2625+0.00000000000000000000000000000000000, -25344.0000000000000000000000000000000,
2626+7920.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2627+0.00000000000000000000000000000000000, +1760.00000000000000000000000000000000,
2628-264.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2629+0.00000000000000000000000000000000000, -24.0000000000000000000000000000000000,
2630+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2631call setResized(root, size(coef, 1, IK) - 1_IK)
2632[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2633F, T, F, F
2634call setPolyRoot(root, count, coef, eigen)
2635count
2636+12
2637root(1:count)
2638+0.866025403784438646763723170731842991, +2.49999999999999999999999999930164047,
2639+0.500000000000000000000000001261300765, +2.86602540378443864676372317070946253,
2640-0.347698086029325849838930767012779505E-28, +3.00000000000000000000000000152269067,
2641-0.500000000000000000000000001265360529, +2.86602540378443864676372317065155482,
2642-0.866025403784438646763723170698404803, +2.49999999999999999999999999929392211,
2643+0.999999999999999999999999999757820376, +1.99999999999999999999999999995932648,
2644-0.999999999999999999999999999750830695, +1.99999999999999999999999999997135064,
2645+0.866025403784438646763723170716402811, +1.50000000000000000000000000003897716,
2646-0.866025403784438646763723170717795451, +1.50000000000000000000000000004211450,
2647+0.499999999999999999999999999996946149, +1.13397459621556135323627682925377416,
2648+0.400031557749517858232708991895941675E-31, +1.00000000000000000000000000000101670,
2649-0.499999999999999999999999999997192042, +1.13397459621556135323627682925417245
2650getPolyVal(coef, root(1:count))
2651-0.494852445845140705534777329001891802E-26, -0.688083924579027547270380241067910289E-26,
2652+0.716877347619594478167908333700731986E-26, -0.143695944266664931679530181469792529E-25,
2653+0.144759920412581771352079250372217687E-25, +0.417237703235191019806716927084944130E-27,
2654+0.751863328766146351737918495571023556E-26, +0.134045217167417378505074447134264243E-25,
2655-0.646037638330747618041935108538337783E-26, +0.660592122032075285851781500567805189E-26,
2656-0.272866987115947983491916910731315757E-26, -0.464639073175175953387508124951561089E-27,
2657-0.310732310566556550151679881864889496E-26, +0.336054745624151029105396368810466934E-27,
2658-0.737190515929035532157260344256763732E-27, +0.264268403249038954812929069369733387E-27,
2659-0.575474030358728112047855988373792555E-27, -0.318305375256678263483632476091604244E-27,
2660-0.686308987542280270708203851796024020E-28, -0.315544362088404722164691426113114492E-29,
2661-0.138050658413677065947052498924487590E-28, +0.480037869299421429879250790270093257E-30,
2662-0.958465999843529343575250206818585269E-28, -0.457539325028186847138802567864016013E-28
2663
2664
2665coef
2666+4095.00000, +0.00000000,
2667+0.00000000, +24576.0000,
2668-67584.0000, +0.00000000,
2669+0.00000000, -112640.000,
2670+126720.000, +0.00000000,
2671+0.00000000, +101376.000,
2672-59136.0000, +0.00000000,
2673+0.00000000, -25344.0000,
2674+7920.00000, +0.00000000,
2675+0.00000000, +1760.00000,
2676-264.000000, +0.00000000,
2677+0.00000000, -24.0000000,
2678+1.00000000, +0.00000000
2679call setResized(root, size(coef, 1, IK) - 1_IK)
2680[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2681F, F, T, F
2682call setPolyRoot(root, count, coef, eigen)
2683count
2684+12
2685root(1:count)
2686-0.102758408E-2, +3.26374292,
2687+0.743275821, +2.94730639,
2688-0.743724287, +2.94551206,
2689+0.972983360, +2.28771806,
2690-0.971354008, +2.28610396,
2691+0.878654838, +1.98345017,
2692+0.860098600, +1.51398087,
2693-0.878169596, +1.98575449,
2694-0.860523164, +1.51400054,
2695+0.499328941, +1.13599277,
2696-0.566091039E-4, +1.00045466,
2697-0.499485791, +1.13598478
2698getPolyVal(coef, root(1:count))
2699+12.4841309, +0.153654099,
2700-2.42480469, -4.67864990,
2701-2.90429688, +5.80480957,
2702-1.59033203, -0.416015625,
2703-1.83007812, +0.395629883,
2704-0.713867188, -0.938720703E-1,
2705-0.152343750, +0.140258789,
2706-0.572753906, -0.150268555,
2707-0.998535156E-1, -0.616455078E-1,
2708-0.258789062E-1, -0.122070312E-2,
2709-0.170898438E-2, -0.675007701E-3,
2710-0.190429688E-1, -0.146484375E-1
2711
2712
2713coef
2714+4095.0000000000000, +0.0000000000000000,
2715+0.0000000000000000, +24576.000000000000,
2716-67584.000000000000, +0.0000000000000000,
2717+0.0000000000000000, -112640.00000000000,
2718+126720.00000000000, +0.0000000000000000,
2719+0.0000000000000000, +101376.00000000000,
2720-59136.000000000000, +0.0000000000000000,
2721+0.0000000000000000, -25344.000000000000,
2722+7920.0000000000000, +0.0000000000000000,
2723+0.0000000000000000, +1760.0000000000000,
2724-264.00000000000000, +0.0000000000000000,
2725+0.0000000000000000, -24.000000000000000,
2726+1.0000000000000000, +0.0000000000000000
2727call setResized(root, size(coef, 1, IK) - 1_IK)
2728[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2729F, F, T, F
2730call setPolyRoot(root, count, coef, eigen)
2731count
2732+12
2733root(1:count)
2734-0.22127855103803995E-10, +3.0000000012083348,
2735+0.50000000092178387, +2.8660254036044090,
2736+0.86602540366466041, +2.4999999995817723,
2737-0.50000000092225982, +2.8660254035707347,
2738-0.86602540364973568, +2.4999999995766795,
2739+0.99999999988689936, +2.0000000000036473,
2740-0.99999999988111377, +2.0000000000065561,
2741+0.86602540376976866, +1.5000000000087796,
2742-0.86602540376847770, +1.5000000000108240,
2743+0.49999999999651829, +1.1339745962147472,
2744+0.18475302723801401E-12, +0.99999999999813760,
2745-0.49999999999610956, +1.1339745962153789
2746getPolyVal(coef, root(1:count))
2747+0.14059878594707698E-7, +0.26553426475682450E-9,
2748+0.46070454118307680E-8, -0.11811152944574133E-7,
2749-0.32819116313476115E-8, -0.20859260985162109E-8,
2750+0.47079993237275630E-8, +0.13283624866744503E-7,
2751-0.23110260372050107E-8, +0.18424088921165094E-8,
2752-0.16898411558941007E-8, +0.26602720026858151E-10,
2753-0.92268237494863570E-9, -0.49340087571181357E-10,
2754-0.29012880986556411E-9, +0.29558577807620168E-10,
2755-0.10641088010743260E-9, -0.33196556614711881E-10,
2756-0.22737367544323206E-11, -0.93223206931725144E-11,
2757+0.19554136088117957E-10, +0.22170363269036277E-11,
2758-0.90949470177292824E-12, +0.60936145018786192E-10
2759
2760
2761coef
2762+4095.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2763+0.00000000000000000000000000000000000, +24576.0000000000000000000000000000000,
2764-67584.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2765+0.00000000000000000000000000000000000, -112640.000000000000000000000000000000,
2766+126720.000000000000000000000000000000, +0.00000000000000000000000000000000000,
2767+0.00000000000000000000000000000000000, +101376.000000000000000000000000000000,
2768-59136.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2769+0.00000000000000000000000000000000000, -25344.0000000000000000000000000000000,
2770+7920.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2771+0.00000000000000000000000000000000000, +1760.00000000000000000000000000000000,
2772-264.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2773+0.00000000000000000000000000000000000, -24.0000000000000000000000000000000000,
2774+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2775call setResized(root, size(coef, 1, IK) - 1_IK)
2776[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2777F, F, T, F
2778call setPolyRoot(root, count, coef, eigen)
2779count
2780+12
2781root(1:count)
2782+0.866025403784438646763723170731842991, +2.49999999999999999999999999930164047,
2783+0.500000000000000000000000001261300765, +2.86602540378443864676372317070946253,
2784-0.347698086029325849838930767012779505E-28, +3.00000000000000000000000000152269067,
2785-0.500000000000000000000000001265360529, +2.86602540378443864676372317065155482,
2786-0.866025403784438646763723170698404803, +2.49999999999999999999999999929392211,
2787+0.999999999999999999999999999757820376, +1.99999999999999999999999999995932648,
2788-0.999999999999999999999999999750830695, +1.99999999999999999999999999997135064,
2789+0.866025403784438646763723170716402811, +1.50000000000000000000000000003897716,
2790-0.866025403784438646763723170717795451, +1.50000000000000000000000000004211450,
2791+0.499999999999999999999999999996946149, +1.13397459621556135323627682925377416,
2792+0.400031557749517858232708991895941675E-31, +1.00000000000000000000000000000101670,
2793-0.499999999999999999999999999997192042, +1.13397459621556135323627682925417245
2794getPolyVal(coef, root(1:count))
2795-0.494852445845140705534777329001891802E-26, -0.688083924579027547270380241067910289E-26,
2796+0.716877347619594478167908333700731986E-26, -0.143695944266664931679530181469792529E-25,
2797+0.144759920412581771352079250372217687E-25, +0.417237703235191019806716927084944130E-27,
2798+0.751863328766146351737918495571023556E-26, +0.134045217167417378505074447134264243E-25,
2799-0.646037638330747618041935108538337783E-26, +0.660592122032075285851781500567805189E-26,
2800-0.272866987115947983491916910731315757E-26, -0.464639073175175953387508124951561089E-27,
2801-0.310732310566556550151679881864889496E-26, +0.336054745624151029105396368810466934E-27,
2802-0.737190515929035532157260344256763732E-27, +0.264268403249038954812929069369733387E-27,
2803-0.575474030358728112047855988373792555E-27, -0.318305375256678263483632476091604244E-27,
2804-0.686308987542280270708203851796024020E-28, -0.315544362088404722164691426113114492E-29,
2805-0.138050658413677065947052498924487590E-28, +0.480037869299421429879250790270093257E-30,
2806-0.958465999843529343575250206818585269E-28, -0.457539325028186847138802567864016013E-28
2807
2808
2809coef
2810+4095.00000, +0.00000000,
2811+0.00000000, +24576.0000,
2812-67584.0000, +0.00000000,
2813+0.00000000, -112640.000,
2814+126720.000, +0.00000000,
2815+0.00000000, +101376.000,
2816-59136.0000, +0.00000000,
2817+0.00000000, -25344.0000,
2818+7920.00000, +0.00000000,
2819+0.00000000, +1760.00000,
2820-264.000000, +0.00000000,
2821+0.00000000, -24.0000000,
2822+1.00000000, +0.00000000
2823call setResized(root, size(coef, 1, IK) - 1_IK)
2824[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2825F, F, F, T
2826call setPolyRoot(root, count, coef, eigen)
2827count
2828+12
2829root(1:count)
2830-0.102758408E-2, +3.26374292,
2831+0.743275821, +2.94730639,
2832-0.743724287, +2.94551206,
2833+0.972983360, +2.28771806,
2834-0.971354008, +2.28610396,
2835+0.878654838, +1.98345017,
2836+0.860098600, +1.51398087,
2837-0.878169596, +1.98575449,
2838-0.860523164, +1.51400054,
2839+0.499328941, +1.13599277,
2840-0.566091039E-4, +1.00045466,
2841-0.499485791, +1.13598478
2842getPolyVal(coef, root(1:count))
2843+12.4841309, +0.153654099,
2844-2.42480469, -4.67864990,
2845-2.90429688, +5.80480957,
2846-1.59033203, -0.416015625,
2847-1.83007812, +0.395629883,
2848-0.713867188, -0.938720703E-1,
2849-0.152343750, +0.140258789,
2850-0.572753906, -0.150268555,
2851-0.998535156E-1, -0.616455078E-1,
2852-0.258789062E-1, -0.122070312E-2,
2853-0.170898438E-2, -0.675007701E-3,
2854-0.190429688E-1, -0.146484375E-1
2855
2856
2857coef
2858+4095.0000000000000, +0.0000000000000000,
2859+0.0000000000000000, +24576.000000000000,
2860-67584.000000000000, +0.0000000000000000,
2861+0.0000000000000000, -112640.00000000000,
2862+126720.00000000000, +0.0000000000000000,
2863+0.0000000000000000, +101376.00000000000,
2864-59136.000000000000, +0.0000000000000000,
2865+0.0000000000000000, -25344.000000000000,
2866+7920.0000000000000, +0.0000000000000000,
2867+0.0000000000000000, +1760.0000000000000,
2868-264.00000000000000, +0.0000000000000000,
2869+0.0000000000000000, -24.000000000000000,
2870+1.0000000000000000, +0.0000000000000000
2871call setResized(root, size(coef, 1, IK) - 1_IK)
2872[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2873F, F, F, T
2874call setPolyRoot(root, count, coef, eigen)
2875count
2876+12
2877root(1:count)
2878-0.22127855103803995E-10, +3.0000000012083348,
2879+0.50000000092178387, +2.8660254036044090,
2880+0.86602540366466041, +2.4999999995817723,
2881-0.50000000092225982, +2.8660254035707347,
2882-0.86602540364973568, +2.4999999995766795,
2883+0.99999999988689936, +2.0000000000036473,
2884-0.99999999988111377, +2.0000000000065561,
2885+0.86602540376976866, +1.5000000000087796,
2886-0.86602540376847770, +1.5000000000108240,
2887+0.49999999999651829, +1.1339745962147472,
2888+0.18475302723801401E-12, +0.99999999999813760,
2889-0.49999999999610956, +1.1339745962153789
2890getPolyVal(coef, root(1:count))
2891+0.14059878594707698E-7, +0.26553426475682450E-9,
2892+0.46070454118307680E-8, -0.11811152944574133E-7,
2893-0.32819116313476115E-8, -0.20859260985162109E-8,
2894+0.47079993237275630E-8, +0.13283624866744503E-7,
2895-0.23110260372050107E-8, +0.18424088921165094E-8,
2896-0.16898411558941007E-8, +0.26602720026858151E-10,
2897-0.92268237494863570E-9, -0.49340087571181357E-10,
2898-0.29012880986556411E-9, +0.29558577807620168E-10,
2899-0.10641088010743260E-9, -0.33196556614711881E-10,
2900-0.22737367544323206E-11, -0.93223206931725144E-11,
2901+0.19554136088117957E-10, +0.22170363269036277E-11,
2902-0.90949470177292824E-12, +0.60936145018786192E-10
2903
2904
2905coef
2906+4095.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2907+0.00000000000000000000000000000000000, +24576.0000000000000000000000000000000,
2908-67584.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2909+0.00000000000000000000000000000000000, -112640.000000000000000000000000000000,
2910+126720.000000000000000000000000000000, +0.00000000000000000000000000000000000,
2911+0.00000000000000000000000000000000000, +101376.000000000000000000000000000000,
2912-59136.0000000000000000000000000000000, +0.00000000000000000000000000000000000,
2913+0.00000000000000000000000000000000000, -25344.0000000000000000000000000000000,
2914+7920.00000000000000000000000000000000, +0.00000000000000000000000000000000000,
2915+0.00000000000000000000000000000000000, +1760.00000000000000000000000000000000,
2916-264.000000000000000000000000000000000, +0.00000000000000000000000000000000000,
2917+0.00000000000000000000000000000000000, -24.0000000000000000000000000000000000,
2918+1.00000000000000000000000000000000000, +0.00000000000000000000000000000000000
2919call setResized(root, size(coef, 1, IK) - 1_IK)
2920[same_type_as(method, sgl), same_type_as(method, eigen), same_type_as(method, jenkins), same_type_as(method, laguerre)]
2921F, F, F, T
2922call setPolyRoot(root, count, coef, eigen)
2923count
2924+12
2925root(1:count)
2926+0.866025403784438646763723170731842991, +2.49999999999999999999999999930164047,
2927+0.500000000000000000000000001261300765, +2.86602540378443864676372317070946253,
2928-0.347698086029325849838930767012779505E-28, +3.00000000000000000000000000152269067,
2929-0.500000000000000000000000001265360529, +2.86602540378443864676372317065155482,
2930-0.866025403784438646763723170698404803, +2.49999999999999999999999999929392211,
2931+0.999999999999999999999999999757820376, +1.99999999999999999999999999995932648,
2932-0.999999999999999999999999999750830695, +1.99999999999999999999999999997135064,
2933+0.866025403784438646763723170716402811, +1.50000000000000000000000000003897716,
2934-0.866025403784438646763723170717795451, +1.50000000000000000000000000004211450,
2935+0.499999999999999999999999999996946149, +1.13397459621556135323627682925377416,
2936+0.400031557749517858232708991895941675E-31, +1.00000000000000000000000000000101670,
2937-0.499999999999999999999999999997192042, +1.13397459621556135323627682925417245
2938getPolyVal(coef, root(1:count))
2939-0.494852445845140705534777329001891802E-26, -0.688083924579027547270380241067910289E-26,
2940+0.716877347619594478167908333700731986E-26, -0.143695944266664931679530181469792529E-25,
2941+0.144759920412581771352079250372217687E-25, +0.417237703235191019806716927084944130E-27,
2942+0.751863328766146351737918495571023556E-26, +0.134045217167417378505074447134264243E-25,
2943-0.646037638330747618041935108538337783E-26, +0.660592122032075285851781500567805189E-26,
2944-0.272866987115947983491916910731315757E-26, -0.464639073175175953387508124951561089E-27,
2945-0.310732310566556550151679881864889496E-26, +0.336054745624151029105396368810466934E-27,
2946-0.737190515929035532157260344256763732E-27, +0.264268403249038954812929069369733387E-27,
2947-0.575474030358728112047855988373792555E-27, -0.318305375256678263483632476091604244E-27,
2948-0.686308987542280270708203851796024020E-28, -0.315544362088404722164691426113114492E-29,
2949-0.138050658413677065947052498924487590E-28, +0.480037869299421429879250790270093257E-30,
2950-0.958465999843529343575250206818585269E-28, -0.457539325028186847138802567864016013E-28
2951
2952
Benchmarks:


Benchmark :: The effects of method on runtime efficiency ⛓

The following program compares the runtime performance of setPolyRoot using different polynomial root finding algorithms.
1! Test the performance of `setPolyRoot()` with and without the selection `control` argument.
2program benchmark
3
4 use pm_bench, only: bench_type
5 use pm_distUnif, only: setUnifRand
6 use pm_arrayResize, only: setResized
7 use pm_kind, only: SK, IK, LK, RKH, RK, RKG => RKD
8 use iso_fortran_env, only: error_unit
9
10 implicit none
11
12 integer(IK) , parameter :: degmax = 9_IK
13 integer(IK) , allocatable :: rootCount(:)
14 integer(IK) :: ibench
15 integer(IK) :: ideg
16 integer(IK) :: degree
17 integer(IK) :: fileUnit
18 integer(IK) :: rootUnit
19 real(RKG) :: dumsum = 0._RKG
20 complex(RKG) :: coef(0:2**degmax)
21 complex(RKG) :: root(2**degmax)
22 type(bench_type) , allocatable :: bench(:)
23
24 bench = [ bench_type(name = SK_"Eigen", exec = setPolyRootEigen, overhead = setOverhead) &
25 , bench_type(name = SK_"Jenkins", exec = setPolyRootJenkins, overhead = setOverhead) &
26 , bench_type(name = SK_"Laguerre", exec = setPolyRootLaguerre, overhead = setOverhead) &
27 , bench_type(name = SK_"SGL", exec = setPolyRootSGL, overhead = setOverhead) &
28 ]
29 allocate(rootCount(size(bench)))
30
31 write(*,"(*(g0,:,' '))")
32 write(*,"(*(g0,:,' '))") "Benchmarking setPolyRoot()"
33 write(*,"(*(g0,:,' '))")
34
35 open(newunit = fileUnit, file = "main.out", status = "replace")
36 open(newunit = rootUnit, file = "root.count", status = "replace")
37
38 write(fileUnit, "(*(g0,:,','))") "Polynomial Degree", (bench(ibench)%name, ibench = 1, size(bench))
39 write(rootUnit, "(*(g0,:,','))") "Polynomial Degree", (bench(ibench)%name, ibench = 1, size(bench))
40 loopOverArraySize: do ideg = 0, degmax
41
42 degree = 2**ideg
43 call setUnifRand(coef(0 : degree), (1._RKG, 1._RKG), (2._RKG, 2._RKG))
44 write(*,"(*(g0,:,' '))") "Benchmarking with coef size", degree
45 do ibench = 1, size(bench)
46 bench(ibench)%timing = bench(ibench)%getTiming(minsec = 0.07_RK)
47 end do
48 write(rootUnit,"(*(g0,:,','))") degree, rootCount
49 write(fileUnit,"(*(g0,:,','))") degree, (bench(ibench)%timing%mean, ibench = 1, size(bench))
50
51 end do loopOverArraySize
52 write(*,"(*(g0,:,' '))") dumsum
53 write(*,"(*(g0,:,' '))")
54
55 close(fileUnit)
56
57contains
58
59 !%%%%%%%%%%%%%%%%%%%%
60 ! procedure wrappers.
61 !%%%%%%%%%%%%%%%%%%%%
62
63 subroutine setOverhead()
64 call getDummy()
65 end subroutine
66
67 subroutine getDummy()
68 dumsum = dumsum + rootCount(ibench)
69 end subroutine
70
71 subroutine setPolyRootEigen()
72 use pm_polynomial, only: setPolyRoot, method => eigen
73 call setPolyRoot(root(1 : degree), rootCount(ibench), coef(0 : degree), method)
74 call getDummy()
75 end subroutine
76
77 subroutine setPolyRootJenkins()
78 use pm_polynomial, only: setPolyRoot, method => jenkins
79 call setPolyRoot(root(1 : degree), rootCount(ibench), coef(0 : degree), method)
80 call getDummy()
81 end subroutine
82
83 subroutine setPolyRootLaguerre()
84 use pm_polynomial, only: setPolyRoot, method => laguerre
85 call setPolyRoot(root(1 : degree), rootCount(ibench), coef(0 : degree), method)
86 call getDummy()
87 end subroutine
88
89 subroutine setPolyRootSGL()
90 use pm_polynomial, only: setPolyRoot, method => sgl
91 call setPolyRoot(root(1 : degree), rootCount(ibench), coef(0 : degree), method)
92 rootCount(ibench) = root(1)%re
93 call getDummy()
94 end subroutine
95
96end program benchmark
pm_bench::getTiming
Generate and return an object of type timing_type containing the benchmark timing information and sta...
Definition: pm_bench.F90:574
pm_distUnif::setUnifRand
Return a uniform random scalar or contiguous array of arbitrary rank of randomly uniformly distribute...
Definition: pm_distUnif.F90:11083
pm_bench
This module contains abstract interfaces and types that facilitate benchmarking of different procedur...
Definition: pm_bench.F90:41
pm_distUnif
This module contains classes and procedures for computing various statistical quantities related to t...
Definition: pm_distUnif.F90:274
pm_kind::RK
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
Definition: pm_kind.F90:543
pm_bench::bench_type
This is the class for creating benchmark and performance-profiling objects.
Definition: pm_bench.F90:386


Example Unix compile command via Intel ifort compiler ⛓

1#!/usr/bin/env sh
2rm main.exe
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe


Example Windows Batch compile command via Intel ifort compiler ⛓

1del main.exe
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
4main.exe


Example Unix / MinGW compile command via GNU gfortran compiler ⛓

1#!/usr/bin/env sh
2rm main.exe
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe


Postprocessing of the benchmark output ⛓

1#!/usr/bin/env python
2
3import matplotlib.pyplot as plt
4import pandas as pd
5import numpy as np
6
7import os
8dirname = os.path.basename(os.getcwd())
9
10fontsize = 14
11
12df = pd.read_csv("main.out", delimiter = ",")
13colnames = list(df.columns.values)
14
15
18
19ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
20ax = plt.subplot()
21
22for colname in colnames[1:]:
23 plt.plot( df[colnames[0]].values
24 , df[colname].values
25 , linewidth = 2
26 )
27
28plt.xticks(fontsize = fontsize)
29plt.yticks(fontsize = fontsize)
30ax.set_xlabel(colnames[0], fontsize = fontsize)
31ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
32ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
33ax.set_xscale("log")
34ax.set_yscale("log")
35plt.minorticks_on()
36plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
37ax.tick_params(axis = "y", which = "minor")
38ax.tick_params(axis = "x", which = "minor")
39ax.legend ( colnames[1:]
40 #, loc='center left'
41 #, bbox_to_anchor=(1, 0.5)
42 , fontsize = fontsize
43 )
44
45plt.tight_layout()
46plt.savefig("benchmark." + dirname + ".runtime.png")
47
48
51
52ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
53ax = plt.subplot()
54
55plt.plot( df[colnames[0]].values
56 , np.ones(len(df[colnames[0]].values))
57 , linestyle = "--"
58 #, color = "black"
59 , linewidth = 2
60 )
61for colname in colnames[2:]:
62 plt.plot( df[colnames[0]].values
63 , df[colname].values / df[colnames[1]].values
64 , linewidth = 2
65 )
66
67plt.xticks(fontsize = fontsize)
68plt.yticks(fontsize = fontsize)
69ax.set_xlabel(colnames[0], fontsize = fontsize)
70ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
71ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}.".format(colnames[1]), fontsize = fontsize)
72ax.set_xscale("log")
73ax.set_yscale("log")
74plt.minorticks_on()
75plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
76ax.tick_params(axis = "y", which = "minor")
77ax.tick_params(axis = "x", which = "minor")
78ax.legend ( colnames[1:]
79 #, bbox_to_anchor = (1, 0.5)
80 #, loc = "center left"
81 , fontsize = fontsize
82 )
83
84plt.tight_layout()
85plt.savefig("benchmark." + dirname + ".runtime.ratio.png")
86
87
90
91df = pd.read_csv("root.count", delimiter = ",")
92colnames = list(df.columns.values)
93
94ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
95ax = plt.subplot()
96
97plt.plot( range(1, df[colnames[0]].values[-1] * 2)
98 , range(1, df[colnames[0]].values[-1] * 2)
99 , linestyle = "--"
100 , color = "black"
101 , linewidth = 2
102 )
103for colname in colnames[1:-1]:
104 plt.plot( df[colnames[0]].values
105 , df[colname].values
106 , linewidth = 2
107 )
108
109plt.xticks(fontsize = fontsize)
110plt.yticks(fontsize = fontsize)
111ax.set_xlabel(colnames[0], fontsize = fontsize)
112ax.set_ylabel("Number of Roots Found", fontsize = fontsize)
113ax.set_title(" vs. ".join(colnames[1:])+"\nHigher is better.", fontsize = fontsize)
114ax.set_xscale("log")
115ax.set_yscale("log")
116plt.minorticks_on()
117plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
118ax.tick_params(axis = "y", which = "minor")
119ax.tick_params(axis = "x", which = "minor")
120ax.legend ( ["Equality"] + list(colnames[1:])
121 #, loc='center left'
122 #, bbox_to_anchor=(1, 0.5)
123 , fontsize = fontsize
124 )
125
126plt.tight_layout()
127plt.savefig("benchmark." + dirname + ".root.count.png")


Visualization of the benchmark output ⛓


Benchmark moral ⛓

  1. Among all root finding algorithms, jenkins_type appears to be the fastest.
  2. The eigen_type method also tends to offer a comparably good performance.
  3. Unlike the above two, laguerre_type algorithm tends to significantly trail behind both in performance and reliability in finding all roots of the polynomial.
Test:
test_pm_polynomial
Todo:
Critical Priority: The current implementation relies on several local allocations, the most important of which are called workspace in the current implementation.
Although this generic interface used to accept a workspace argument, it was subsequently removed in favor of simplicity.
A new set of interfaces can be added in the future to allow specification of scratch space arguments to avoid repeated local allocations.
This could boost performance when this generic interface is called many times repeatedly.
Todo:
Critical Priority: The generic interface for the Eigenvalue method internally uses the eigenvalue computing routine of EISPACK for upper Hessenberg matrices to compute the roots of the polynomial.
This internal implementation should be substituted with the corresponding external routine once it is implemented in the ParaMonte library.
Todo:
Low Priority: The existing implementations of the algorithms for the Jenkins-Traub method contain relics of F77 coding style in the form of a few goto statements.
These remaining goto statements should be carefully removed in the future.
Todo:
Critical Priority: The method of Skowron-Gould must be fully implemented.
Todo:
Normal Priority: A benchmark comparing the runtime performances of the complex vs. real coefficient routines of this module should be added here.


Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Copyright © 1996 California Institute of Technology, Pasadena, California. ALL RIGHTS RESERVED. Based on Government Sponsored Research NAS7-03001. Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met: Redistributions of source code must retain this copyright notice, this list of conditions and the following disclaimer. Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution. Neither the name of the California Institute of Technology (Caltech) nor the names of its contributors may be used to endorse or promote products derived from this software without specific prior written permission. THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE. For those codes indicated with a Math a la Carte copyright, the same rules apply, except without the full force of the Caltech legal team. When citing this software we request that you also mention the names of the people who wrote the software you are using. Designed by C. L. Lawson, JPL, May 1986. Programmed by C. L. Lawson and S. Y. Chiu, JPL, May 1986, Feb. 1987.
Author:
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan Fatemeh Bagheri, Friday 09:51 AM, September 6, 2024, NASA Goddard Space Flight Center, Washington, D.C.

Definition at line 4619 of file pm_polynomial.F90.

The documentation for this interface was generated from the following file: