This module contains the procedures and interfaces for computing the cumulative sum of the exponential of an array without undue numerical overflow. More...

Data Types
interface	getCumPropExp
	Generate and return the cumulative sum of the proportions of the exponential of the input array, optionally in the backward direction and, optionally reverse the output cumulative sum upon return. More...

interface	setCumPropExp
	Return the cumulative sum of the proportions of the exponential of the input array, optionally in the backward direction and, optionally reverse the output cumulative sum upon return. More...

Functions/Subroutines
pure real(RKG) function, dimension(lenArray)	getCumPropExp_RK (array, maxArray, lenArray)
	[LEGACY code] Generate and return the normalized cumulative sum (i.e., Cumulative Density Function (CDF)) of the exponentials of the input real vector robustly (without overflow or underflow). The last element of the returned vector is one. More...

Variables
character(*, SK), parameter	MODULE_NAME = "@pm_mathCumPropExp"

Detailed Description

This module contains the procedures and interfaces for computing the cumulative sum of the exponential of an array without undue numerical overflow.

Benchmarks:

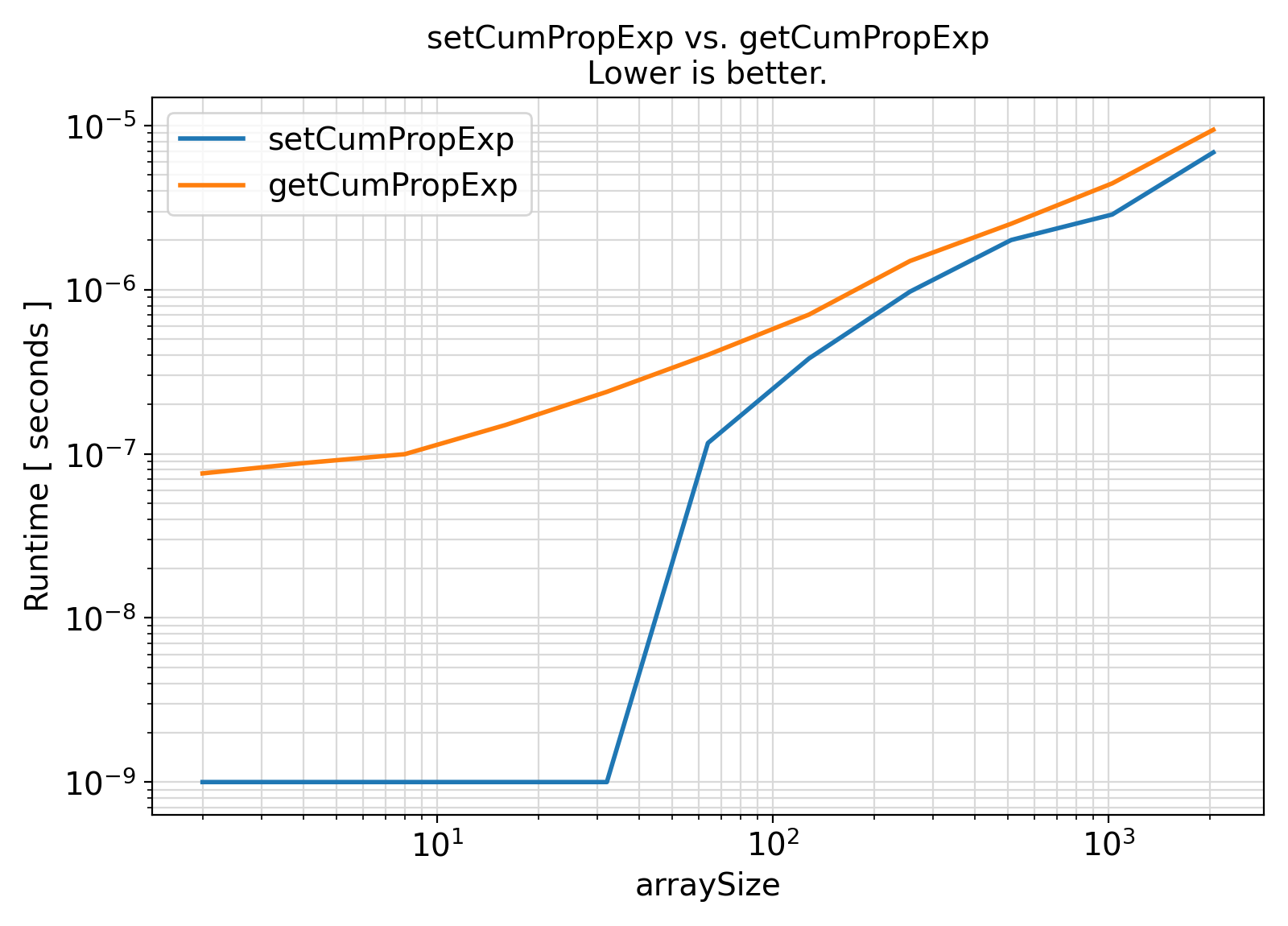
Benchmark :: The runtime performance of getCumPropExp vs. setCumPropExp ⛓

! Test the performance of `getCumPropExp()` vs. `setCumPropExp()`.
program benchmark
 
    use iso_fortran_env, only: error_unit
    use pm_bench, only: bench_type
    use pm_kind, only: IK, RK, SK
 
    implicit none
 
    integer(IK)                         :: i
    integer(IK)                         :: iarr
    integer(IK)                         :: fileUnit
    integer(IK)     , parameter         :: NARR = 11_IK
    integer(IK)                         :: arraySize(NARR)
    real(RK)                            :: dummySum = 0._RK
    real(RK)                            :: maxArray
    real(RK)        , allocatable       :: array(:)
    real(RK)        , allocatable       :: cumPropExp(:)
    type(bench_type), allocatable       :: bench(:)
 
    bench = [ bench_type(name = SK_"setCumPropExp", exec = setCumPropExp , overhead = setOverhead) &
            , bench_type(name = SK_"getCumPropExp", exec = getCumPropExp , overhead = setOverhead) &
            ]
 
    arraySize = [( 2_IK**iarr, iarr = 1_IK, NARR )]
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "getCumPropExp() vs. setCumPropExp()"
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,','))") "arraySize", (bench(i)%name, i = 1, size(bench))
 
        loopOverArraySize: do iarr = 1, NARR
 
            allocate(array(arraySize(iarr)))
            allocate(cumPropExp(arraySize(iarr)), source = 0._RK)
            write(*,"(*(g0,:,' '))") "Benchmarking with array size", arraySize(iarr)
 
            do i = 1, size(bench)
                bench(i)%timing = bench(i)%getTiming(minsec = 0.1_RK)
            end do
            write(fileUnit,"(*(g0,:,','))") arraySize(iarr), (bench(i)%timing%mean, i = 1, size(bench))
 
            deallocate(array, cumPropExp)
 
        end do loopOverArraySize
        write(*,"(*(g0,:,' '))") dummySum
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call getArray()
        call getDummy()
    end subroutine
 
    subroutine getArray()
        call random_number(array)
        maxArray = maxval(array)
    end subroutine
 
    subroutine getDummy()
        dummySum = dummySum + cumPropExp(1)
    end subroutine
 
    subroutine getCumPropExp()
        block
            use pm_mathCumPropExp, only: getCumPropExp
            call getArray()
            cumPropExp = getCumPropExp(array, maxArray)
            call getDummy()
        end block
    end subroutine
 
    subroutine setCumPropExp()
        block
            use pm_mathCumPropExp, only: setCumPropExp, sequence
            call getArray()
            call setCumPropExp(cumPropExp, array, maxArray, sequence)
            call getDummy()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ",")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓

The procedures under the generic interface getCumPropExp are functions while the procedures under the generic interface setCumPropExp are subroutines.
From the benchmark results, it appears that the functional interface performs significantly worse than the procedural interface.
However, the difference appears to diminish toward larger array sizes.

Test:: test_pm_mathCumPropExp

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Amir Shahmoradi, April 25, 2015, 2:21 PM, National Institute for Fusion Studies, The University of Texas Austin

Function/Subroutine Documentation

◆ getCumPropExp_RK()

pure real(RKG) function, dimension(lenArray) pm_mathCumPropExp::getCumPropExp_RK	(	real(RKG), dimension(lenArray), intent(in)	array,
		real(RKG)	maxArray,
		integer(IK)	lenArray
	)

[LEGACY code]
Generate and return the normalized cumulative sum (i.e., Cumulative Density Function (CDF)) of the exponentials of the input real vector robustly (without overflow or underflow). The last element of the returned vector is one.

Parameters

[in]	array	: The input `contiguous` vector of log-values whose log-sum-exp must be computed.
[in]	maxArray	: The maximum of the input `array` argument (`maxArray = maxval(array)`).
[in]	lenArray	: The length of the input array.

Returns: cumPropExp : A real vector of the same length as the input array array.

Warning: This routine is only kept for backward compatibility and should not be used in production code. Instead, use the procedures under the generic interface setCumPropExp.

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Test:: test_pm_mathCumPropExp

Author:: Amir Shahmoradi, April 25, 2015, 2:21 PM, National Institute for Fusion Studies, The University of Texas Austin

Definition at line 2128 of file pm_mathCumPropExp.F90.

References pm_kind::RK.

Variable Documentation

◆ MODULE_NAME

character(*, SK), parameter pm_mathCumPropExp::MODULE_NAME = "@pm_mathCumPropExp"

Definition at line 59 of file pm_mathCumPropExp.F90.

Data Types

Functions/Subroutines

Variables

Detailed Description

Function/Subroutine Documentation

◆ getCumPropExp_RK()

Variable Documentation

◆ MODULE_NAME