ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation.
Data Types | Variables
pm_distanceMahal Module Reference

This module contains classes and procedures for computing the Mahalanobis statistical distance. More...

Data Types

interface  getDisMahalSq
 Generate and return the square of the Mahalanobis distance of a (set of npnt) point(s) from a single (or a set of nsam independent) sample(s) characterized by a (set of) Multivariate Normal (MVN) distribution(s) in ndim dimensions. More...
 
interface  setDisMahalSq
 Return the square of the Mahalanobis distance of a (set of npnt) point(s) from a single (or a set of nsam independent) sample(s) characterized by a (set of) Multivariate Normal (MVN) distribution(s) in ndim dimensions. More...
 

Variables

character(*, SK), parameter MODULE_NAME = "@pm_distanceMahal"
 

Detailed Description

This module contains classes and procedures for computing the Mahalanobis statistical distance.

The Mahalanobis distance of an observation \(\vec{x} = (x_1, x_2, x_3, \ldots, x_N)^\mathsf{H}\) from a set of observations represented by a Multivariate Normal (MVN) distribution in \(N\) dimensions with \((\bu{\mu}, \bu{\Sigma})\) as its mean vector and covariance matrix is defined as,

\begin{equation} \large D_M( \vec{x} ) = \sqrt{ (\vec{x} - \bu{\mu})^\mathsf{H} ~ \bu{\Sigma}^{-1} (\vec{x} - \bu{\mu}) }~, \end{equation}

where \(^{H}\) stands for the Hermitian transpose.
When the Covariance of the MVN distribution is the Identity matrix, the Mahalanobis distance simply becomes the Euclidean norm.

Benchmarks:


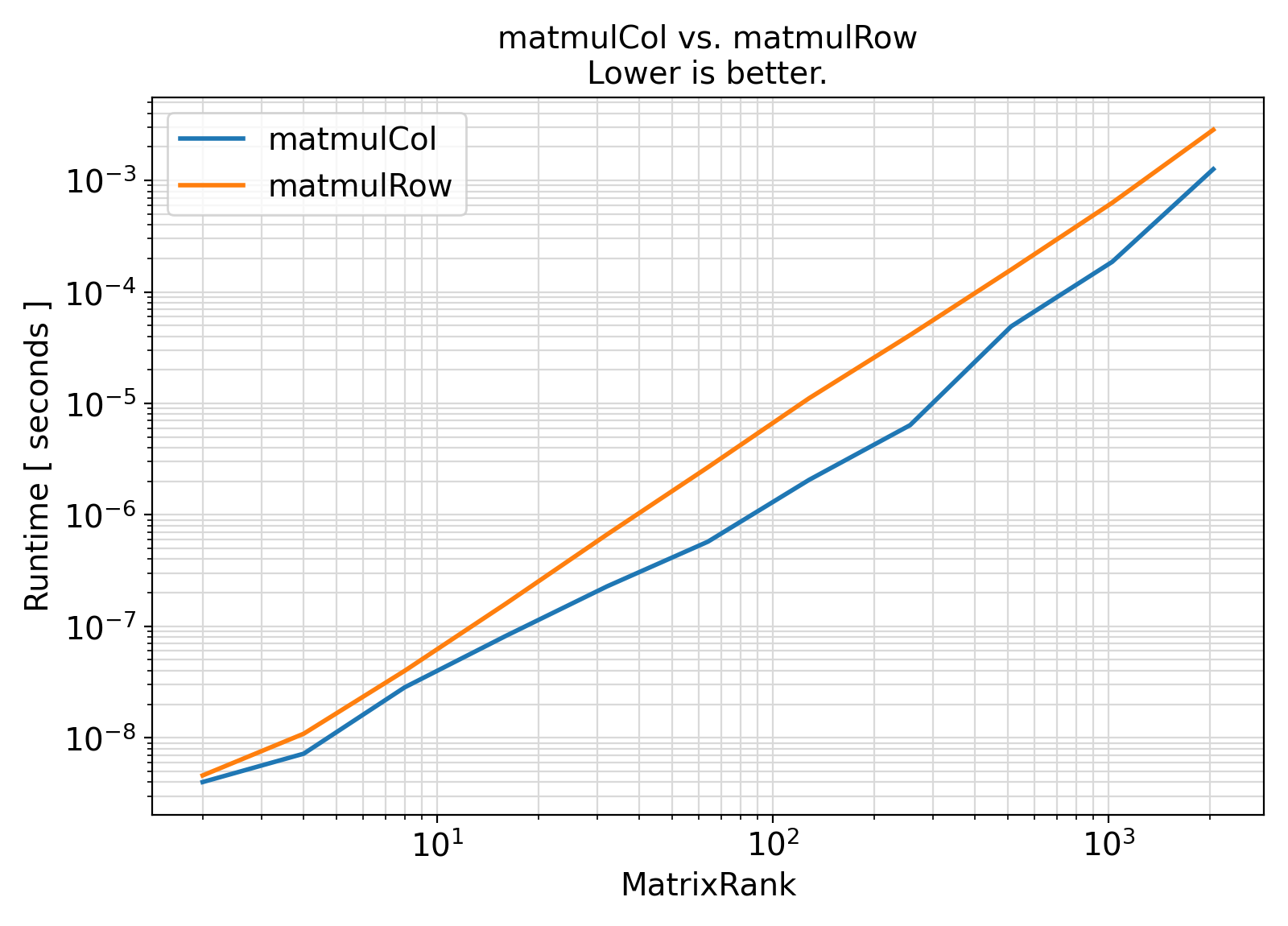
Benchmark :: The runtime performance of getDisMahalSq vs. setDisMahalSq ⛓

1! Test the performance of `row-major()` vs. `column-major()` matrix multiplication.
2program benchmark
3
4 use pm_bench, only: bench_type
5 use iso_fortran_env, only: error_unit
6 use pm_kind, only: IK, RKG => RK, RK, SK
7 use pm_distUnif, only: getUnifRand
8
9 implicit none
10
11 integer(IK) :: i
12 integer(IK) :: fileUnit
13 integer(IK) :: rank, irank
14 integer(IK) , parameter :: NRANK = 11_IK
15 real(RKG) :: dummySum = 0._RKG
16 real(RKG) , allocatable :: matA(:,:), matB(:), matC(:), matD(:)
17 type(bench_type), allocatable :: bench(:)
18
19 bench = [ bench_type(name = SK_"matmulCol", exec = matmulCol, overhead = setOverhead) &
20 , bench_type(name = SK_"matmulRow", exec = matmulRow, overhead = setOverhead) &
21 ]
22
23 open(newunit = fileUnit, file = "main.out", status = "replace")
24
25 write(fileUnit, "(*(g0,:,', '))") "MatrixRank", (bench(i)%name, i = 1, size(bench))
26
27 loopOverMatrixRank: do irank = 1, NRANK
28
29 rank = 2_IK**irank
30 matD = getUnifRand(0._RKG, 1._RKG, rank)
31 matC = getUnifRand(0._RKG, 1._RKG, rank)
32 matB = getUnifRand(0._RKG, 1._RKG, rank)
33 matA = getUnifRand(0._RKG, 1._RKG, rank, rank)
34
35 write(*,"(*(g0,:,' '))") "Benchmarking with rank", rank
36
37 do i = 1, size(bench)
38 bench(i)%timing = bench(i)%getTiming(minsec = 0.07_RK)
39 end do
40
41 write(fileUnit,"(*(g0,:,', '))") rank, (bench(i)%timing%mean, i = 1, size(bench))
42
43 end do loopOverMatrixRank
44 write(*,"(*(g0,:,' '))") dummySum
45 write(*,"(*(g0,:,' '))")
46
47 close(fileUnit)
48
49contains
50
51 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
52 ! procedure wrappers.
53 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
54
55 subroutine setOverhead()
56 call getDummy()
57 end subroutine
58
59 subroutine getDummy()
60 if (all(matD == matC)) dummySum = dummySum + matC(1) + matD(1)
61 end subroutine
62
63 subroutine matmulRow()
64 matC = matmul(matA, matB)
65 call getDummy()
66 end subroutine
67
68 subroutine matmulCol()
69 matD = matmul(matB, matA)
70 call getDummy()
71 end subroutine
72
73end program benchmark
pm_bench::getTiming
Generate and return an object of type timing_type containing the benchmark timing information and sta...
Definition: pm_bench.F90:574
pm_distUnif::getUnifRand
Generate and return a scalar or a contiguous array of rank 1 of length s1 of randomly uniformly distr...
Definition: pm_distUnif.F90:4150
pm_bench
This module contains abstract interfaces and types that facilitate benchmarking of different procedur...
Definition: pm_bench.F90:41
pm_distUnif
This module contains classes and procedures for computing various statistical quantities related to t...
Definition: pm_distUnif.F90:274
pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268
pm_kind::RK
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
Definition: pm_kind.F90:543
pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540
pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539
pm_bench::bench_type
This is the class for creating benchmark and performance-profiling objects.
Definition: pm_bench.F90:386

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Postprocessing of the benchmark output ⛓
1#!/usr/bin/env python
2
3import matplotlib.pyplot as plt
4import pandas as pd
5import numpy as np
6
7import os
8dirname = os.path.basename(os.getcwd())
9
10fontsize = 14
11
12df = pd.read_csv("main.out", delimiter = ", ")
13colnames = list(df.columns.values)
14
15
18
19ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
20ax = plt.subplot()
21
22for colname in colnames[1:]:
23 plt.plot( df[colnames[0]].values
24 , df[colname].values
25 , linewidth = 2
26 )
27
28plt.xticks(fontsize = fontsize)
29plt.yticks(fontsize = fontsize)
30ax.set_xlabel(colnames[0], fontsize = fontsize)
31ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
32ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
33ax.set_xscale("log")
34ax.set_yscale("log")
35plt.minorticks_on()
36plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
37ax.tick_params(axis = "y", which = "minor")
38ax.tick_params(axis = "x", which = "minor")
39ax.legend ( colnames[1:]
40 #, loc='center left'
41 #, bbox_to_anchor=(1, 0.5)
42 , fontsize = fontsize
43 )
44
45plt.tight_layout()
46plt.savefig("benchmark." + dirname + ".runtime.png")
47
48
51
52ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
53ax = plt.subplot()
54
55plt.plot( df[colnames[0]].values
56 , np.ones(len(df[colnames[0]].values))
57 , linestyle = "--"
58 #, color = "black"
59 , linewidth = 2
60 )
61for colname in colnames[2:]:
62 plt.plot( df[colnames[0]].values
63 , df[colname].values / df[colnames[1]].values
64 , linewidth = 2
65 )
66
67plt.xticks(fontsize = fontsize)
68plt.yticks(fontsize = fontsize)
69ax.set_xlabel(colnames[0], fontsize = fontsize)
70ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
71ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
72ax.set_xscale("log")
73#ax.set_yscale("log")
74plt.minorticks_on()
75plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
76ax.tick_params(axis = "y", which = "minor")
77ax.tick_params(axis = "x", which = "minor")
78ax.legend ( colnames[1:]
79 #, bbox_to_anchor = (1, 0.5)
80 #, loc = "center left"
81 , fontsize = fontsize
82 )
83
84plt.tight_layout()
85plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓
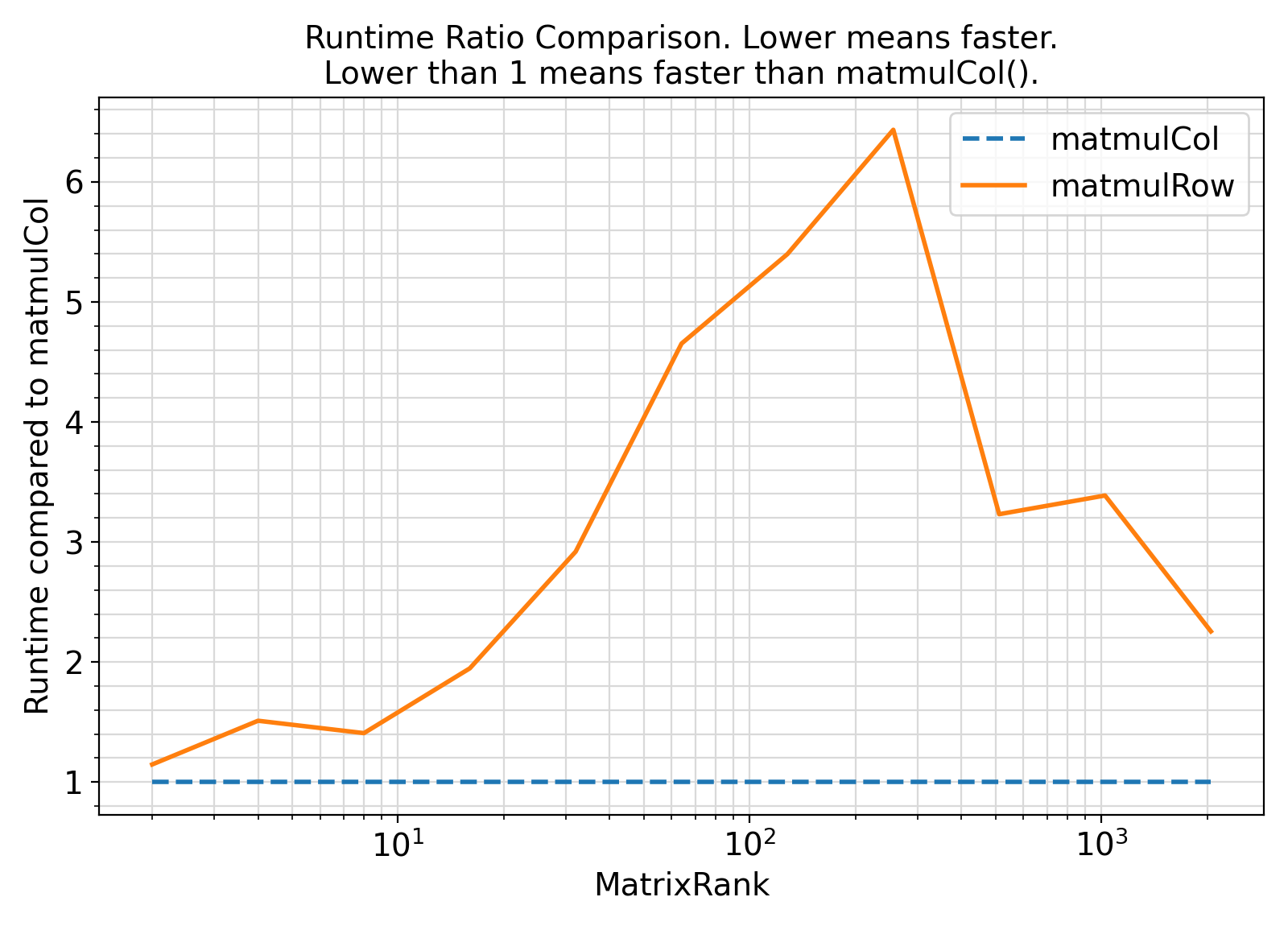
  1. Fortran is a column-major language, meaning that matrix elements are stored column-wise in computer memory.
  2. As such, matrix multiplication format that respects column-major order of Fortran, is significantly faster than the row-major matrix multiplication.
  3. This is particularly relevant when one matrix is symmetric square and the other is a vector, which is the case with the procedures of the generic interface getDisMahalSq.


Benchmark :: The runtime performance of getDisMahalSq vs. setDisMahalSq ⛓

1program benchmark
2
3 use pm_bench, only: bench_type
4 use iso_fortran_env, only: error_unit
5 use pm_kind, only: IK, RKG => RK, RK, SK
6 use pm_distUnif, only: getUnifRand
7
8 implicit none
9
10 integer(IK) :: fileUnit
11 integer(IK) :: i, isim, nsim
12 integer(IK) :: rank, irank
13 integer(IK) , parameter :: NRANK = 10_IK
14 real(RKG) :: dummySum = 0._RKG
15 real(RKG) :: dummyOne = 0._RKG
16 real(RKG) :: dummyTwo = 0._RKG
17 real(RKG) , allocatable :: matA(:,:), matB(:)
18 type(bench_type), allocatable :: bench(:)
19
20 bench = [ bench_type(name = SK_"loop_and_dotp", exec = loop_and_dotp, overhead = setOverhead) &
21 , bench_type(name = SK_"dotp_matmul", exec = dotp_matmul, overhead = setOverhead) &
22 ]
23
24 open(newunit = fileUnit, file = "main.out", status = "replace")
25
26 write(fileUnit, "(*(g0,:,', '))") "MatrixRank", (bench(i)%name, i = 1, size(bench))
27
28 loopOverMatrixRank: do irank = 1, NRANK
29
30 rank = 2_IK**irank
31 nsim = nint(2.**NRANK / rank)
32 matB = getUnifRand(0._RKG, 1._RKG, rank)
33 matA = getUnifRand(0._RKG, 1._RKG, rank, rank)
34
35 write(*,"(*(g0,:,' '))") "Benchmarking with rank", rank
36
37 do i = 1, size(bench)
38 bench(i)%timing = bench(i)%getTiming(minsec = 0.07_RK)
39 end do
40
41 write(fileUnit,"(*(g0,:,', '))") rank, (bench(i)%timing%mean / nsim, i = 1, size(bench))
42
43 end do loopOverMatrixRank
44 write(*,"(*(g0,:,' '))") dummySum
45 write(*,"(*(g0,:,' '))")
46
47 close(fileUnit)
48
49contains
50
51 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
52 ! procedure wrappers.
53 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
54
55 subroutine setOverhead()
56 do isim = 1, nsim
57 call getDummy()
58 end do
59 end subroutine
60
61 subroutine getDummy()
62 dummySum = dummySum + dummyOne + dummyTwo
63 end subroutine
64
65 subroutine loop_and_dotp()
66 integer(IK) :: i, sizeB
67 sizeB = size(matB, 1, IK)
68 dummyOne = 0._RKG
69 do isim = 1, nsim
70 do i = 1, sizeB
71 dummyOne = dummyOne + matB(i) * dot_product(matB, matA(1:sizeB, i))
72 end do
73 call getDummy()
74 end do
75 end subroutine
76
77 subroutine dotp_matmul()
78 do isim = 1, nsim
79 dummyTwo = dot_product(matB, matmul(matB, matA))
80 call getDummy()
81 end do
82 end subroutine
83
84end program benchmark

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Postprocessing of the benchmark output ⛓
1#!/usr/bin/env python
2
3import matplotlib.pyplot as plt
4import pandas as pd
5import numpy as np
6
7import os
8dirname = os.path.basename(os.getcwd())
9
10fontsize = 14
11
12df = pd.read_csv("main.out", delimiter = ", ")
13colnames = list(df.columns.values)
14
15
18
19ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
20ax = plt.subplot()
21
22for colname in colnames[1:]:
23 plt.plot( df[colnames[0]].values
24 , df[colname].values
25 , linewidth = 2
26 )
27
28plt.xticks(fontsize = fontsize)
29plt.yticks(fontsize = fontsize)
30ax.set_xlabel(colnames[0], fontsize = fontsize)
31ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
32ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
33ax.set_xscale("log")
34ax.set_yscale("log")
35plt.minorticks_on()
36plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
37ax.tick_params(axis = "y", which = "minor")
38ax.tick_params(axis = "x", which = "minor")
39ax.legend ( colnames[1:]
40 #, loc='center left'
41 #, bbox_to_anchor=(1, 0.5)
42 , fontsize = fontsize
43 )
44
45plt.tight_layout()
46plt.savefig("benchmark." + dirname + ".runtime.png")
47
48
51
52ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
53ax = plt.subplot()
54
55plt.plot( df[colnames[0]].values
56 , np.ones(len(df[colnames[0]].values))
57 , linestyle = "--"
58 #, color = "black"
59 , linewidth = 2
60 )
61for colname in colnames[2:]:
62 plt.plot( df[colnames[0]].values
63 , df[colname].values / df[colnames[1]].values
64 , linewidth = 2
65 )
66
67plt.xticks(fontsize = fontsize)
68plt.yticks(fontsize = fontsize)
69ax.set_xlabel(colnames[0], fontsize = fontsize)
70ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
71ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
72ax.set_xscale("log")
73#ax.set_yscale("log")
74plt.minorticks_on()
75plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
76ax.tick_params(axis = "y", which = "minor")
77ax.tick_params(axis = "x", which = "minor")
78ax.legend ( colnames[1:]
79 #, bbox_to_anchor = (1, 0.5)
80 #, loc = "center left"
81 , fontsize = fontsize
82 )
83
84plt.tight_layout()
85plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

Visualization of the benchmark output ⛓

Benchmark moral ⛓
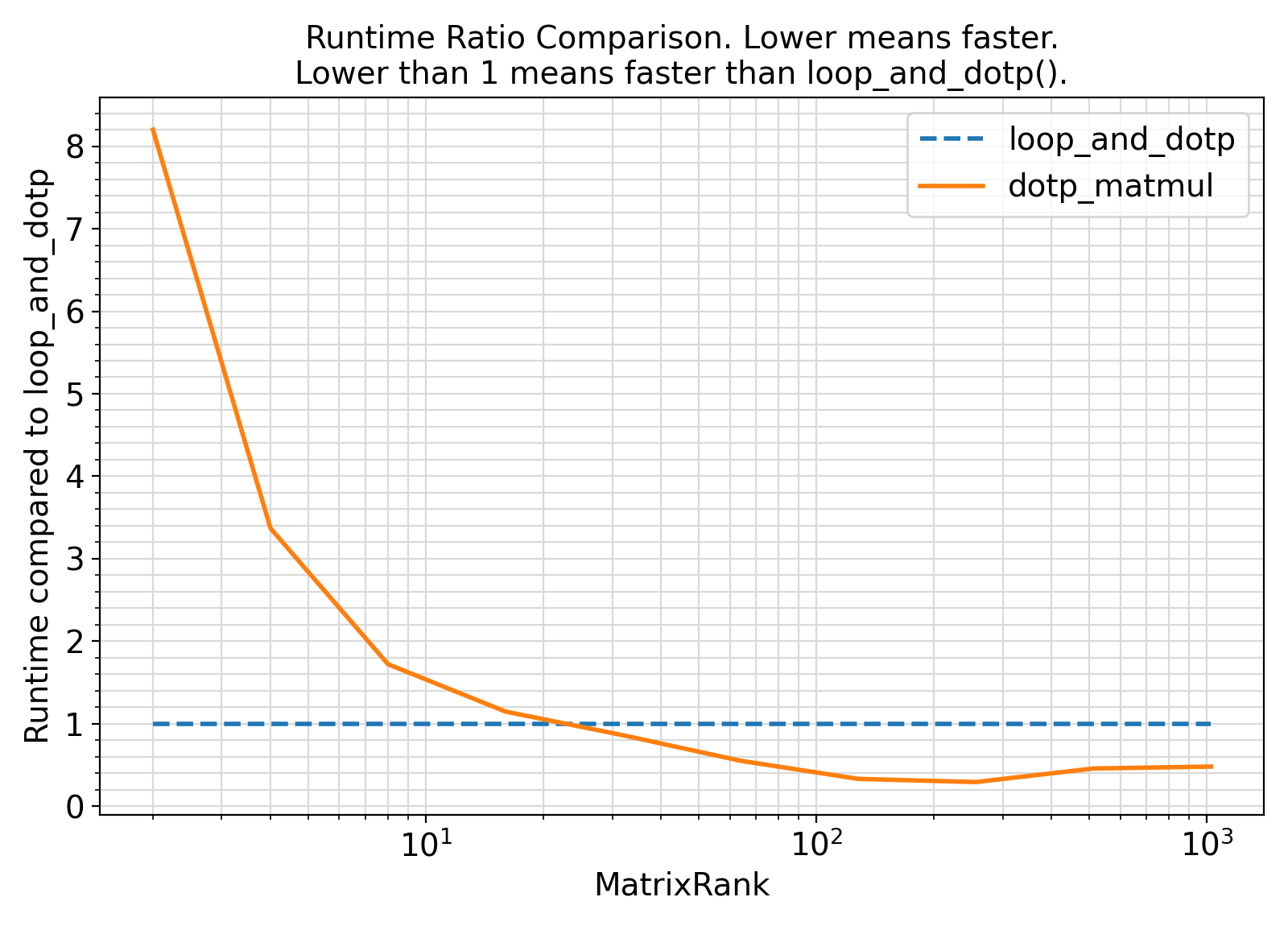
  1. The procedures in this benchmark compute the Mahalanobis distance using two different implementations.
    1. The procedure named loop_and_dotp computes the distance via looping and Fortran intrinsic dot_product().
      This approach avoids temporary array creations.
    2. The procedure named dotp_matmul uses the all-intrinsic expression dot_product(vec, matmul(vec, mat)) to compute the distance.
  2. Based on the benchmark results, it appears that the looping version offers a faster implementation.
  3. Additionally, the specification of the slice of the matrix in the dot product of the looping approach significantly improves the performance.
Test:
test_pm_distanceMahal


Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Amir Shahmoradi, March 22, 2012, 2:21 PM, National Institute for Fusion Studies, The University of Texas Austin

Variable Documentation

◆ MODULE_NAME

character(*, SK), parameter pm_distanceMahal::MODULE_NAME = "@pm_distanceMahal"

Definition at line 88 of file pm_distanceMahal.F90.