This module contains classes and procedures for computing various statistical quantities related to the Poisson distribution.
More...
This module contains classes and procedures for computing various statistical quantities related to the Poisson distribution.
Specifically, this module contains routines for computing the following quantities of the Poisson distribution:
-
the Probability Mass Function (PMF)
-
the Cumulative Distribution Function (CDF)
-
the Random Number Generation from the distribution (RNG)
-
the Inverse Cumulative Distribution Function (ICDF) or the Quantile Function
The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event.
It is named after French mathematician Siméon Denis Poisson.
The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area, or volume.
A discrete random variable X is said to have a Poisson distribution, with parameter \lambda > 0 if it has a probability mass function given by,
\begin{equation}
f(k; \lambda) = \pi(X = k) = \frac {\lambda^k \exp\left(-\lambda\right)}{k!} ~,
\end{equation}
where
-
k is the number of occurrences ( k = 0, 1, 2, \ldots), and
-
\ms{!} is the factorial function.
The positive real number \lambda is equal to the expected value of X and also to its variance.
\begin{equation}
\lambda = \up{E}(X) = \up{Var}(X) ~.
\end{equation}
The CDF of the Poisson distribution with parameter \lambda is defined as,
\begin{eqnarray}
\ms{CDF}(k | \lambda)
&=& \frac{\Gamma(\lfloor k + 1 \rfloor, \lambda)}{\lfloor k \rfloor !} ~, \nonumber \\
&=& \exp\left(-\lambda\right) \sum _{j=0}^{\lfloor k \rfloor}{\frac{\lambda^{j}}{j!}} ~,
\end{eqnarray}
where
-
k is the number of occurrences ( k = 0, 1, 2, \ldots), and
-
\ms{!} is the factorial function, and
-
\Gamma(x, y) / \lfloor k \rfloor ! is the regularized upper incomplete gamma function, and
-
\lfloor k \rfloor is the floor function.
Random Number Generation
The RNG generic interfaces of this module use two different approaches for Poisson RNG for different ranges of \lambda parameter values of the Poisson distribution.
-
When \lambda < LAMBDA_LIMIT, a RNG algorithm due to Donald Ervin Knuth is used.
-
When LAMBDA_LIMIT \leq \lambda, a rejection-based RNG algorithm due to Hormann, 1993, The transformed rejection method for generating Poisson random variables is used.
This rejection method has an efficiency slight less than 90\%.
- See also
- pm_distPois
pm_distPois
Poisson distribution
- Benchmarks:
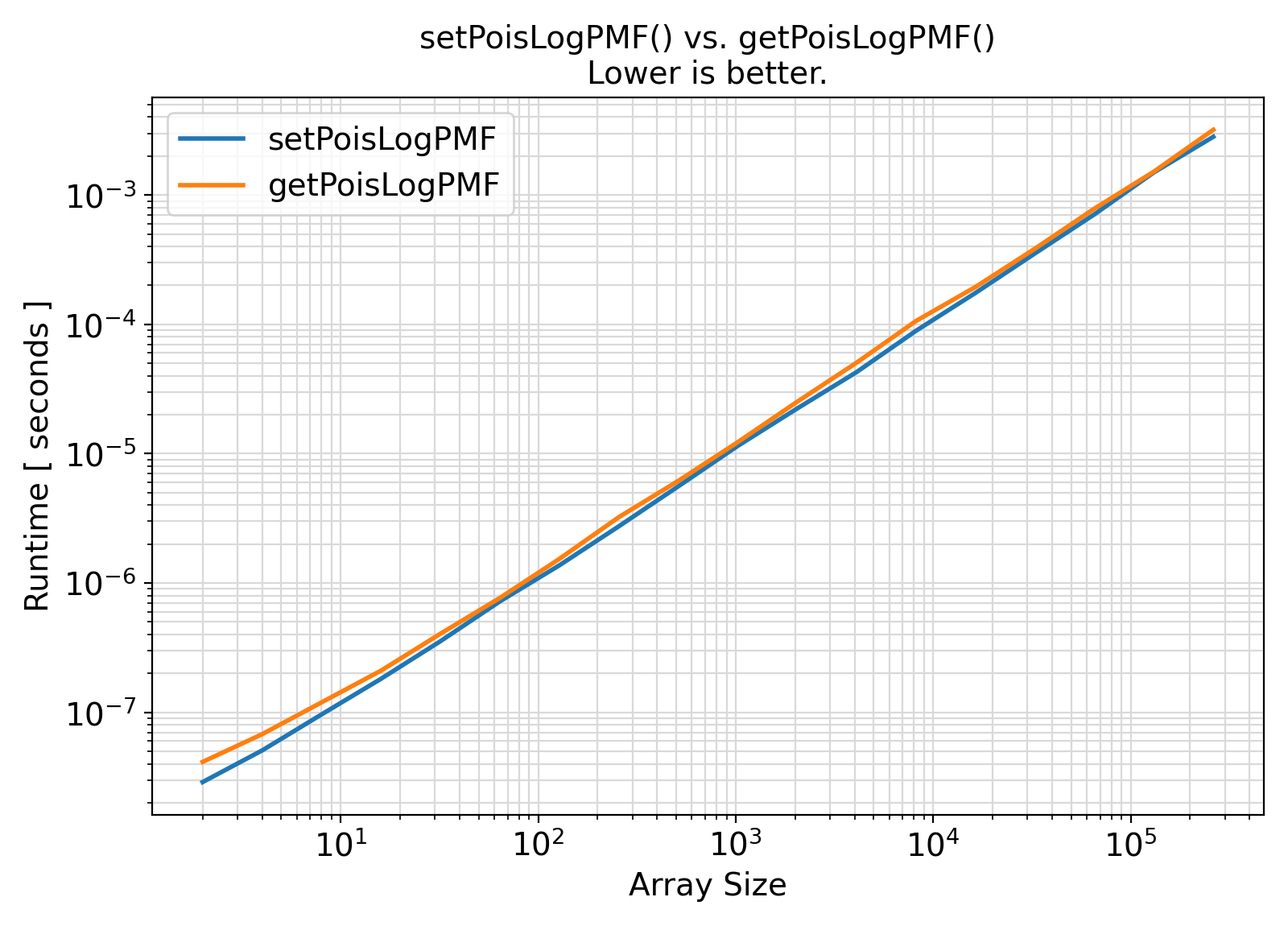
Benchmark :: The runtime performance of getPoisLogPMF vs. setPoisLogPMF ⛓
4 use iso_fortran_env,
only:
error_unit
13 integer(IK) :: fileUnit
14 integer(IK) ,
parameter :: NSIZE
= 18_IK
15 integer(IK) ,
parameter :: NBENCH
= 2_IK
16 integer(IK) :: arraySize(NSIZE)
17 integer(IK) ,
allocatable ::
count(:)
18 real(RKG) ,
allocatable :: array(:)
19 real(RKG) :: dummy
= 0._RKG
20 type(bench_type) :: bench(NBENCH)
21 type(xoshiro256ssw_type) :: rng
25 bench(
1)
= bench_type(name
= SK_
"getPoisLogPMF", exec
= getPoisLogPMF , overhead
= setOverhead)
26 bench(
2)
= bench_type(name
= SK_
"setPoisLogPMF", exec
= setPoisLogPMF , overhead
= setOverhead)
28 arraySize
= [(
2_IK**isize, isize
= 1_IK, NSIZE )]
30 write(
*,
"(*(g0,:,' '))")
31 write(
*,
"(*(g0,:,' vs. '))") (bench(i)
%name, i
= 1, NBENCH)
32 write(
*,
"(*(g0,:,' '))")
34 open(newunit
= fileUnit, file
= "main.out", status
= "replace")
36 write(fileUnit,
"(*(g0,:,','))")
"arraySize", (bench(i)
%name, i
= 1, NBENCH)
38 loopOverarraySize:
do isize
= 1, NSIZE
40 write(
*,
"(*(g0,:,' '))")
"Benchmarking with size", arraySize(isize)
42 allocate(array(arraySize(isize)),
count(arraySize(isize)))
44 bench(i)
%timing
= bench(i)
%getTiming(minsec
= 0.05_RK)
46 deallocate(array, count)
48 write(fileUnit,
"(*(g0,:,','))") arraySize(isize), (bench(i)
%timing
%mean, i
= 1, NBENCH)
50 end do loopOverarraySize
52 write(
*,
"(*(g0,:,' '))") dummy
53 write(
*,
"(*(g0,:,' '))")
63 subroutine setOverhead()
68 subroutine initialize()
74 dummy
= dummy
+ array(
1)
77 subroutine setPoisLogPMF()
86 subroutine getPoisLogPMF()
Generate and return an object of type timing_type containing the benchmark timing information and sta...
Generate and return the natural logarithm of the Probability Mass Function (PMF) of the Poisson distr...
Return the natural logarithm of the Probability Mass Function (PMF) of the Poisson distribution for a...
Return a uniform random scalar or contiguous array of arbitrary rank of randomly uniformly distribute...
This module contains abstract interfaces and types that facilitate benchmarking of different procedur...
This module contains classes and procedures for computing various statistical quantities related to t...
This module contains classes and procedures for computing various statistical quantities related to t...
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
This is the class for creating benchmark and performance-profiling objects.
This is the derived type for declaring and generating objects of type xoshiro256ssw_type containing a...
Example Unix compile command via Intel ifort compiler ⛓
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example Windows Batch compile command via Intel ifort compiler ⛓
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
Example Unix / MinGW compile command via GNU gfortran compiler ⛓
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Postprocessing of the benchmark output ⛓
3import matplotlib.pyplot
as plt
9methods = [
"setPoisLogPMF",
"getPoisLogPMF"]
11df = pd.read_csv(
"main.out")
17ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
21 plt.plot( df[
"arraySize"].values
26plt.xticks(fontsize = fontsize)
27plt.yticks(fontsize = fontsize)
28ax.set_xlabel(
"Array Size", fontsize = fontsize)
29ax.set_ylabel(
"Runtime [ seconds ]", fontsize = fontsize)
30ax.set_title(
"setPoisLogPMF() vs. getPoisLogPMF()\nLower is better.", fontsize = fontsize)
34plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
35ax.tick_params(axis =
"y", which =
"minor")
36ax.tick_params(axis =
"x", which =
"minor")
44plt.savefig(
"benchmark.getPoisLogPMF_vs_setPoisLogPMF.runtime.png")
50ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
53plt.plot( df[
"arraySize"].values
54 , np.ones(len(df[
"arraySize"].values))
59plt.plot( df[
"arraySize"].values
60 , df[
"getPoisLogPMF"].values / df[
"setPoisLogPMF"].values
64plt.xticks(fontsize = fontsize)
65plt.yticks(fontsize = fontsize)
66ax.set_xlabel(
"Array Size", fontsize = fontsize)
67ax.set_ylabel(
"Runtime compared to setPoisLogPMF()", fontsize = fontsize)
68ax.set_title(
"getPoisLogPMF() / setPoisLogPMF()\nLower means faster. Lower than 1 means faster than setPoisLogPMF().", fontsize = fontsize)
72plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
73ax.tick_params(axis =
"y", which =
"minor")
74ax.tick_params(axis =
"x", which =
"minor")
75ax.legend ( [
"setPoisLogPMF",
"getPoisLogPMF"]
82plt.savefig(
"benchmark.getPoisLogPMF_vs_setPoisLogPMF.runtime.ratio.png")
Visualization of the benchmark output ⛓
Benchmark moral ⛓
- The procedures under the generic interface getPoisLogPMF are functions while the procedures under the generic interface setPoisLogPMF are subroutines.
From the benchmark results, it appears that the functional interface performs slightly less efficiently than the subroutine interface when the input array size is small.
Otherwise, the difference appears to be marginal and insignificant in most practical situations.
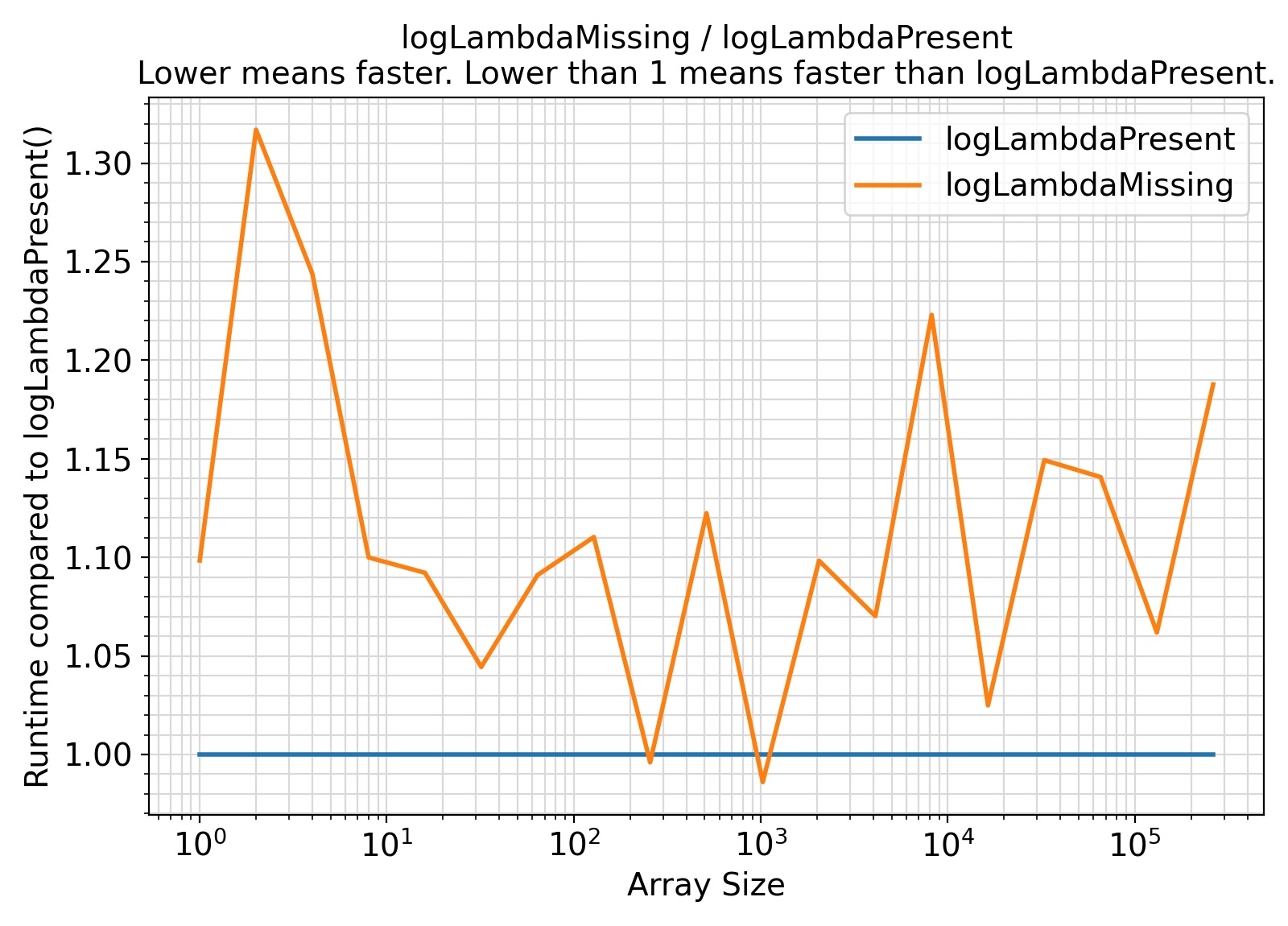
Benchmark :: The runtime performance of setPoisLogPMF with and without logLambda ⛓
3 use iso_fortran_env,
only:
error_unit
13 integer(IK) :: fileUnit
14 integer(IK) ,
parameter :: NSIZE
= 18_IK
15 integer(IK) ,
parameter :: NBENCH
= 2_IK
16 integer(IK) :: arraySize(
0:NSIZE)
17 integer(IK) ,
allocatable ::
count(:)
18 real(RKG) ,
allocatable :: logPMF(:)
19 real(RKG) ,
allocatable :: logLambda(:), lambda(:)
20 real(RKG) :: dummy
= 0._RKG
21 type(bench_type) :: bench(NBENCH)
22 type(xoshiro256ssw_type) :: rng
26 bench(
1)
= bench_type(name
= SK_
"logLambdaMissing", exec
= logLambdaMissing , overhead
= setOverhead)
27 bench(
2)
= bench_type(name
= SK_
"logLambdaPresent", exec
= logLambdaPresent , overhead
= setOverhead)
29 arraySize
= [(
2_IK**isize, isize
= 0_IK, NSIZE )]
31 write(
*,
"(*(g0,:,' '))")
32 write(
*,
"(*(g0,:,' vs. '))") (bench(i)
%name, i
= 1, NBENCH)
33 write(
*,
"(*(g0,:,' '))")
35 open(newunit
= fileUnit, file
= "main.out", status
= "replace")
37 write(fileUnit,
"(*(g0,:,','))")
"arraySize", (bench(i)
%name, i
= 1, NBENCH)
39 loopOverarraySize:
do isize
= 0, NSIZE
41 write(
*,
"(*(g0,:,' '))")
"Benchmarking with size", arraySize(isize)
43 allocate(logPMF(arraySize(isize)),
count(arraySize(isize)), lambda(arraySize(isize)))
45 call random_number(lambda)
46 lambda
= 1._RKG - lambda
47 logLambda
= log(lambda)
49 bench(i)
%timing
= bench(i)
%getTiming(minsec
= 0.05_RK)
51 deallocate(logPMF, count, lambda)
53 write(fileUnit,
"(*(g0,:,','))") arraySize(isize), (bench(i)
%timing
%mean, i
= 1, NBENCH)
55 end do loopOverarraySize
57 write(
*,
"(*(g0,:,' '))") dummy
58 write(
*,
"(*(g0,:,' '))")
68 subroutine setOverhead()
73 subroutine initialize()
79 dummy
= dummy
+ logPMF(
1)
82 subroutine logLambdaPresent()
85 if (arraySize(isize)
> 1_IK)
then
88 call setPoisLogPMF(logPMF(
1),
count(
1), lambda(
1), logLambda(
1))
93 subroutine logLambdaMissing()
96 if (arraySize(isize)
> 1_IK)
then
Example Unix compile command via Intel ifort compiler ⛓
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example Windows Batch compile command via Intel ifort compiler ⛓
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
Example Unix / MinGW compile command via GNU gfortran compiler ⛓
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Postprocessing of the benchmark output ⛓
3import matplotlib.pyplot
as plt
9methods = [
"logLambdaPresent",
"logLambdaMissing"]
11df = pd.read_csv(
"main.out")
17ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
21 plt.plot( df[
"arraySize"].values
26plt.xticks(fontsize = fontsize)
27plt.yticks(fontsize = fontsize)
28ax.set_xlabel(
"Array Size", fontsize = fontsize)
29ax.set_ylabel(
"Runtime [ seconds ]", fontsize = fontsize)
30ax.set_title(
"logLambdaPresent() vs. logLambdaMissing()\nLower is better.", fontsize = fontsize)
34plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
35ax.tick_params(axis =
"y", which =
"minor")
36ax.tick_params(axis =
"x", which =
"minor")
44plt.savefig(
"benchmark.setPoisLogPMF-logLambda-missing_vs_present.runtime.png")
50ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
53plt.plot( df[
"arraySize"].values
54 , np.ones(len(df[
"arraySize"].values))
59plt.plot( df[
"arraySize"].values
60 , df[
"logLambdaMissing"].values / df[
"logLambdaPresent"].values
64plt.xticks(fontsize = fontsize)
65plt.yticks(fontsize = fontsize)
66ax.set_xlabel(
"Array Size", fontsize = fontsize)
67ax.set_ylabel(
"Runtime compared to logLambdaPresent()", fontsize = fontsize)
68ax.set_title(
"logLambdaMissing / logLambdaPresent\nLower means faster. Lower than 1 means faster than logLambdaPresent.", fontsize = fontsize)
72plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
73ax.tick_params(axis =
"y", which =
"minor")
74ax.tick_params(axis =
"x", which =
"minor")
75ax.legend ( [
"logLambdaPresent",
"logLambdaMissing"]
82plt.savefig(
"benchmark.setPoisLogPMF-logLambda-missing_vs_present.runtime.ratio.png")
Visualization of the benchmark output ⛓
Benchmark moral ⛓
- The procedures under the generic interface setPoisLogPMF accept an extra argument
logLambda = log(lambda) while the procedures under the generic interface getPoisLogPMF compute this term internally with every procedure call.
In the presence of this argument, the logarithmic computation log(lambda) will be avoided.
As such, the presence of logLambda is expected to lead to faster computations.
- Test:
- test_pm_distPois
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
-
If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
-
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
- Copyright
- Computational Data Science Lab
- Author:
- Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan