pm_parallelism::setForkJoinScaling Interface Reference

Return the predicted parallel Fork-Join speedup scaling behavior for simulations whose image contributions are stochastically accepted only from the first successful image starting from image ID 1. More...

Detailed Description

Return the predicted parallel Fork-Join speedup scaling behavior for simulations whose image contributions are stochastically accepted only from the first successful image starting from image ID 1.

This generic interface can be used to compute theoretical speedup gained by a Fork-Join parallel simulation where the probability of contribution of an image to the simulation is less than 1, meaning that image contributions are stochastic at each step of the Fork-Join cycle.
If the image contributions are inspected sequentially from the first image to last and only the first successful image contribution is kept in the simulation, then it can be shown that the contribution of the images to the parallel Fork-Join simulation follows a Cyclic Geometric Distribution.
See Amir Shahmoradi, Fatemeh Bagheri (2020). ParaDRAM: A Cross-Language Toolbox for Parallel High-Performance Delayed-Rejection Adaptive Metropolis Markov Chain Monte Carlo Simulations. for theoretical details.

Parameters

[in]	conProb	: The input scalar of, type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), containing the average probability of contribution of each image to the Fork-Join simulation. For example, conProb can be the effective acceptance rate in parallel Fork-Join Monte Carlo or MCMC sampling simulations where each image is tasked with returning a single proposal state for subsequent evaluation and if is first to be accepted accepted, for usage in the next simulation step.
[in]	seqSecTime	: The input scalar of the same type and kind as conProb containing the time (in seconds) per image (or process or thread) of the inherently-sequential sections of the entire Fork-Join simulation.
[in]	parSecTime	: The input scalar of the same type and kind as conProb containing the time (in seconds) per image (or process or thread) of the inherently-parallel sections of the entire Fork-Join simulation.
[in]	comSecTime	: The input scalar of the same type and kind as conProb containing the time (in seconds) per image (or process or thread) of the pairwise inter-process communication sections of the entire Fork-Join simulation. Assuming all rooter images communicate only with the main image and the entire communication takes overhead seconds, then comSecTime = overhead / (nproc - 1) with nproc representing the total number of images.
[out]	scaling	: The output allocatable vector of the same type and kind as the input conProb containing the predicted speedup scaling of the stochastic Fork-Join simulation under a range of possible image (or thread or process) counts given in the output numproc. On output, the vector scaling will be resized until the maximum speedup and the corresponding image count is identified in the scaling. The ith element of scaling represents theoretically-predicted speedup if numproc(i) images (threads or processes) were used in the parallel Fork-Join simulation.
[out]	numproc	: The output allocatable vector of type integer of default kind IK containing the number of images for the speedup reported in the corresponding element of scaling. If the input argument comSecTime is positive, then numproc is simply a linear range of integers starting with 1 with a jump size of 1. If the input argument comSecTime is positive, then numproc is simply a log(2)-linear range of integers starting with 1 with a jump size of 1.
[in]	scalingMaxVal	: The output scalar of the same type and kind as the input conProb containing the maximum achievable speedup (corresponding to maxval(scaling)).
[in]	scalingMaxLoc	: The output scalar of type integer of default kind IK containing the index of element of the output scaling containing scalingMaxVal (i.e., maxloc(scaling)).
[out]	scalingMinLen	: The input positive scalar of type integer of default kind IK containing the minimum size of the output scaling. (optional, default = int(2 / max(conProb, 0.001)))

Possible calling interfaces ⛓

use pm_parallelism, only: setForkJoinScaling
 
call setForkJoinScaling(conProb, seqSecTime, parSecTime, comSecTime, scaling, numproc, scalingMaxVal, scalingMaxLoc, scalingMinLen = scalingMinLen)
!

Warning

The condition 0 <= seqSecTime must hold for the corresponding input arguments.
The condition 0 <= parSecTime must hold for the corresponding input arguments.
The condition 0 <= comSecTime must hold for the corresponding input arguments.
The condition 0 <= scalingMinLen must hold for the corresponding input arguments.
The condition 0 <= conProb .and. conProb <= 1 must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

See also

pm_sampling
pm_distGeomCyclic
Amir Shahmoradi, Fatemeh Bagheri (2020). ParaDRAM: A Cross-Language Toolbox for Parallel High-Performance Delayed-Rejection Adaptive Metropolis Markov Chain Monte Carlo Simulations.

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK, LK, RKG => RKD
    use pm_parallelism, only: setForkJoinScaling
    use pm_arraySpace, only: getLinSpace
    use pm_distUnif, only: getUnifRand
    use pm_io, only: display_type
 
    implicit none
 
    type(display_type) :: disp
    real(RKG) :: redshift = 5.5_RKG
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!Compute the Fisher z transformation of a random bounded variable.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    block
        use pm_kind, only: RKG => RKS
        integer(IK), allocatable :: numproc(:)
        real, allocatable :: scaling(:)
        integer :: maxloc
        real :: maxval
        call disp%skip()
        call disp%show("call setForkJoinScaling(conProb = .23, seqSecTime = 0., parSecTime = 1., comSecTime = .001, scaling = scaling, numproc = numproc, scalingMaxVal = maxval, scalingMaxLoc = maxloc)")
                        call setForkJoinScaling(conProb = .23, seqSecTime = 0., parSecTime = 1., comSecTime = .001, scaling = scaling, numproc = numproc, scalingMaxVal = maxval, scalingMaxLoc = maxloc)
        call disp%show("scaling")
        call disp%show( scaling )
        call disp%show("numproc")
        call disp%show( numproc )
        call disp%show("maxloc")
        call disp%show( maxloc )
        call disp%show("maxval")
        call disp%show( maxval )
        call disp%skip()
    end block
 
    ! Generate both the cosmic rate and the rate density.
 
    block
        use pm_io, only: getErrTableWrite
        real :: maxval
        integer :: maxloc
        real, allocatable :: scaling(:)
        integer(IK), allocatable :: numproc(:)
        call setForkJoinScaling(conProb = .23, seqSecTime = 0., parSecTime = 1., comSecTime = .001, scaling = scaling, numproc = numproc, scalingMaxVal = maxval, scalingMaxLoc = maxloc, scalingMinLen = 32_IK)
        if (0 /= getErrTableWrite("setForkJoinScaling.csv", reshape([real(numproc), scaling], [size(numproc), 2]), header = "Processor Count,Scaling")) error stop "Table writing failed."
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!Compute the Fisher z transformation of a random bounded variable.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
call setForkJoinScaling(conProb = .23, seqSecTime = 0., parSecTime = 1., comSecTime = .001, scaling = scaling, numproc = numproc, scalingMaxVal = maxval, scalingMaxLoc = maxloc)
scaling
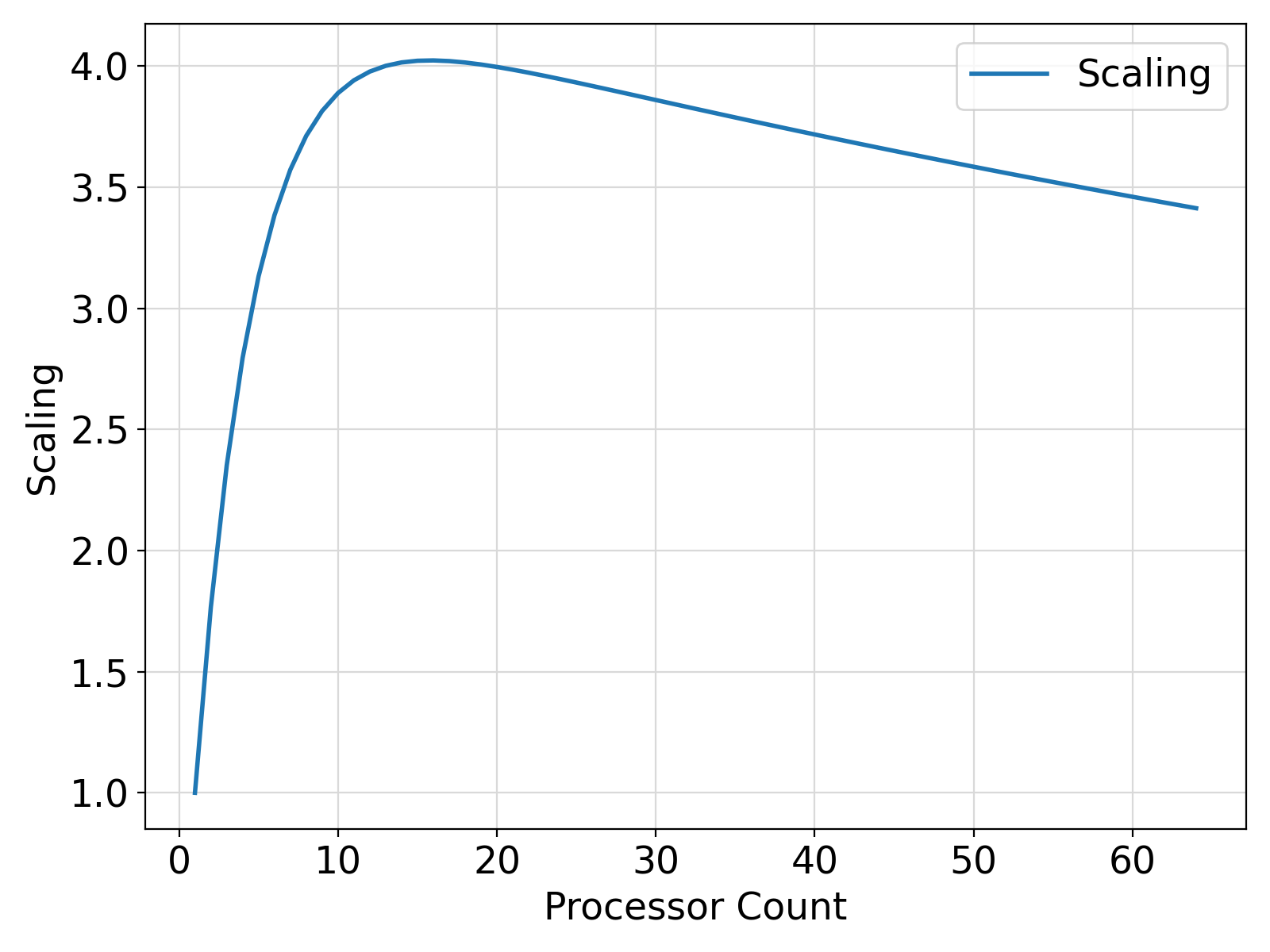
+1.00000000, +1.76687264, +2.35178590, +2.79578543, +3.13124704, +3.38341904, +3.57183909, +3.71154809, +3.81408238, +3.88827229, +3.94086552, +3.97701430, +4.00064898, +4.01476812, +4.02165937, +4.02306509, +4.02031755, +4.01442909, +4.00617361, +3.99614286, +3.98478413, +3.97244120, +3.95937586, +3.94578743, +3.93182707, +3.91761041, +3.90322590, +3.88874030, +3.87420368, +3.85965514, +3.84512305, +3.83063030, +3.81619239, +3.80182147, +3.78752732, +3.77331614, +3.75919294, +3.74516082, +3.73122287, +3.71738029, +3.70363355, +3.68998289, +3.67642927, +3.66297197, +3.64961052, +3.63634515, +3.62317395, +3.61009741, +3.59711385, +3.58422279, +3.57142329, +3.55871487, +3.54609632, +3.53356671, +3.52112484, +3.50877047, +3.49650216, +3.48431945, +3.47222137, +3.46020651, +3.44827533, +3.43642521, +3.42465687, +3.41296887, +3.40135980, +3.38982987, +3.37837839, +3.36700320, +3.35570431, +3.34448123, +3.33333325, +3.32225871
numproc
+1, +2, +3, +4, +5, +6, +7, +8, +9, +10, +11, +12, +13, +14, +15, +16, +17, +18, +19, +20, +21, +22, +23, +24, +25, +26, +27, +28, +29, +30, +31, +32, +33, +34, +35, +36, +37, +38, +39, +40, +41, +42, +43, +44, +45, +46, +47, +48, +49, +50, +51, +52, +53, +54, +55, +56, +57, +58, +59, +60, +61, +62, +63, +64, +65, +66, +67, +68, +69, +70, +71, +72
maxloc
+16
maxval
+4.02306509
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
#pip install paramonte
 
import os
examname = os.path.basename(os.getcwd())
 
 
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
fontsize = 17
 
df = pd.read_csv(examname + ".csv", delimiter = ",")
 
fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
ax = plt.subplot()
 
for colname in df.columns[1:]:
    plt.plot( df.values[:, 0]
            , df[colname].values
            , linestyle = "-"
            , linewidth = 2
            )
 
labels = []
for colname in list(df.columns[1:]): labels.append(colname)
ax.legend   ( labels
            , fontsize = fontsize
           #, loc = "center left"
           #, bbox_to_anchor = (1, 0.5)
            )
 
ax.set_xlabel(df.columns[0], fontsize = fontsize)
ax.set_ylabel(df.columns[1], fontsize = fontsize)
 
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
 
plt.tight_layout()
plt.savefig(examname + ".png")

Visualization of the example output ⛓

Test:

test_pm_parallelism

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, Tuesday March 7, 2017, 4:13 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 229 of file pm_parallelism.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_parallelism.F90