pm_matrixTrans::setMatTrans Interface Reference

Generate and return the transpose of the input matrix of arbitrary type and kind using a cache-oblivious approach.
More...

Detailed Description

Generate and return the transpose of the input matrix of arbitrary type and kind using a cache-oblivious approach.

In computing, a cache-oblivious (or cache-transcendent) algorithm is a method designed to take advantage of a processor cache without having the size of the cache (or the length of the cache lines, etc.) as an explicit parameter.
An optimal cache-oblivious algorithm is a cache-oblivious algorithm that uses the cache optimally.
Thus, a cache-oblivious algorithm is designed to perform well, without modification, on multiple machines with different cache sizes, or for a memory hierarchy with different levels of cache having different sizes.
Cache-oblivious algorithms are contrasted with explicit loop tiling, which explicitly breaks a problem into blocks that are optimally sized for a given cache.

Typically, a cache-oblivious algorithm works by a recursive divide-and-conquer algorithm, where the problem is divided into smaller and smaller subproblems.
Eventually, one reaches a subproblem size that fits into the cache, regardless of the cache size.
For example, an optimal cache-oblivious matrix multiplication is obtained by recursively dividing each matrix into four sub-matrices to be multiplied, multiplying the submatrices in a depth-first fashion.
In tuning for a specific machine, one may use a hybrid algorithm which uses loop tiling tuned for the specific cache sizes at the bottom level but otherwise uses the cache-oblivious algorithm.

Parameters

[in,out]	source	: The input/output matrix (of rank 2) of either type character of kind any supported by the processor (e.g., SK, SKA, SKD , or SKU) or, type integer of kind any supported by the processor (e.g., IK, IK8, IK16, IK32, or IK64) or, type logical of kind any supported by the processor (e.g., LK) or, type complex of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128) or, type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128) or, whose contents will be Symmetric or Hermitian transposed. If the output matrix argument destin is missing, the result of transposition will be written to source. This is possible only if the input source is a square matrix. If the output matrix argument destin is present, the result of transposition will be written to destin. As such, the input source has intent(in) will not be modified by the algorithm.
[out]	destin	: The output matrix of the same type and kind, but transposed shape of source containing the transposition. (optional. If missing, the transposition result will be written to the input source, in which case, source must be square.)
[in]	bsize	: The input positive scalar integer of default kind IK representing the minimum submatrix size. Any input source or subset of it whose size along both dimensions is below bsize will be transposed via the default Fortran transpose() procedure. (optional. default = 32)
[in]	operation	: The input scalar that can be, the constant transHerm exclusively when source is of type complex of kind any supported by the processor (e.g., CK, CK32, CK64, or CK128). implying that a Hermitian transpose of the specified subset of source is to be computed and stored. This argument is merely a convenience to differentiate the different procedure functionalities within this generic interface. (optional. If missing, the Symmetric transposition will be returned for complex matrices.)

Possible calling interfaces ⛓

use pm_matrixTrans, only: setMatTrans, transHerm
 
call setMatTrans(source(1:ndim,1:ndim))
call setMatTrans(source(1:ndim,1:ndim), bsize)
call setMatTrans(source(1:ndim,1:ndim), operation)
call setMatTrans(source(1:ndim,1:ndim), operation, bsize)
call setMatTrans(source(1:nrow,1:ncol), destin(1:ncol,1:nrow))
call setMatTrans(source(1:nrow,1:ncol), destin(1:ncol,1:nrow), bsize)
call setMatTrans(source(1:nrow,1:ncol), destin(1:ncol,1:nrow), operation)
call setMatTrans(source(1:nrow,1:ncol), destin(1:ncol,1:nrow), operation, bsize)

Warning

The condition 0 < bsize must hold for the corresponding input arguments.
The condition size(source, 1) == size(source, 2) must hold when the output argument destin is missing.
The condition size(source, 1) == size(destin, 2) .and. size(source, 2) == size(destin, 1) must hold for the corresponding input arguments.

The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

Remarks

Based on some relevant benchmarks performed, the contiguous attribute for the input arguments does not appear to have any noticeable impact on the performance of the algorithm in the release optimized compilation modes.

See also

pm_matrixCopy

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK, LK, CK, RK
    use pm_matrixSubset, only: dia, uppDia, lowDia, uppLow, uppLowDia
    use pm_distUnif, only: setUnifRand
    use pm_matrixTrans, only: setMatTrans
    use pm_io, only: display_type
 
    implicit none
 
    type(display_type)  :: disp
    disp = display_type(file = "main.out.F90")
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    block
 
        character(2) :: matA(5,10), matB(10,5)
 
        call disp%skip()
        call disp%show("call setUnifRand(matA, 'AA', 'ZZ')")
                        call setUnifRand(matA, 'AA', 'ZZ')
        call disp%show("matA")
        call disp%show( matA , deliml = SK_"""" )
        call disp%show("call setMatTrans(matA, matB)")
                        call setMatTrans(matA, matB)
        call disp%show("matB")
        call disp%show( matB , deliml = SK_"""" )
        call disp%skip()
 
    end block
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    block
 
        character(2) :: matA(10,10)
 
        call disp%skip()
        call disp%show("call setUnifRand(matA, 'AA', 'ZZ')")
                        call setUnifRand(matA, 'AA', 'ZZ')
        call disp%show("matA")
        call disp%show( matA , deliml = SK_"""" )
        call disp%show("call setMatTrans(matA)")
                        call setMatTrans(matA)
        call disp%show("matA")
        call disp%show( matA , deliml = SK_"""" )
        call disp%skip()
 
    end block
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
call setUnifRand(matA, 'AA', 'ZZ')
matA
"HK", "GH", "PS", "LI", "TR", "HN", "HT", "WH", "RI", "DY"
"EV", "ZU", "OS", "HM", "AB", "IL", "HO", "OZ", "LA", "QJ"
"JQ", "HY", "OB", "AI", "JP", "AS", "RP", "YC", "PN", "UM"
"CS", "CS", "BQ", "CE", "UM", "QR", "RF", "IK", "UW", "JY"
"MD", "NW", "HC", "BA", "OT", "YG", "RY", "II", "PD", "MA"
call setMatTrans(matA, matB)
matB
"HK", "EV", "JQ", "CS", "MD"
"GH", "ZU", "HY", "CS", "NW"
"PS", "OS", "OB", "BQ", "HC"
"LI", "HM", "AI", "CE", "BA"
"TR", "AB", "JP", "UM", "OT"
"HN", "IL", "AS", "QR", "YG"
"HT", "HO", "RP", "RF", "RY"
"WH", "OZ", "YC", "IK", "II"
"RI", "LA", "PN", "UW", "PD"
"DY", "QJ", "UM", "JY", "MA"
 
 
call setUnifRand(matA, 'AA', 'ZZ')
matA
"QH", "CU", "EY", "YM", "BH", "HK", "DZ", "DV", "YV", "ZY"
"GI", "RY", "VY", "XR", "WU", "JQ", "AK", "BP", "AI", "XR"
"OB", "OS", "CT", "ZV", "LG", "WY", "OB", "XJ", "QR", "EC"
"YG", "OG", "ZX", "WJ", "YP", "GQ", "ZU", "TF", "HQ", "UF"
"DH", "WQ", "KY", "IO", "CB", "TJ", "MJ", "GQ", "MY", "KF"
"CY", "XB", "SH", "NV", "ST", "JX", "KO", "WH", "OA", "LZ"
"KF", "YC", "JG", "FL", "GY", "LE", "PL", "ZR", "JE", "YI"
"AS", "IR", "ZW", "IQ", "MG", "XZ", "XT", "MW", "EO", "UO"
"BA", "FD", "FL", "LB", "IV", "MH", "BS", "HB", "OK", "XR"
"YB", "BO", "IY", "YR", "NV", "PP", "WW", "NR", "VO", "HX"
call setMatTrans(matA)
matA
"QH", "GI", "OB", "YG", "DH", "CY", "KF", "AS", "BA", "YB"
"CU", "RY", "OS", "OG", "WQ", "XB", "YC", "IR", "FD", "BO"
"EY", "VY", "CT", "ZX", "KY", "SH", "JG", "ZW", "FL", "IY"
"YM", "XR", "ZV", "WJ", "IO", "NV", "FL", "IQ", "LB", "YR"
"BH", "WU", "LG", "YP", "CB", "ST", "GY", "MG", "IV", "NV"
"HK", "JQ", "WY", "GQ", "TJ", "JX", "LE", "XZ", "MH", "PP"
"DZ", "AK", "OB", "ZU", "MJ", "KO", "PL", "XT", "BS", "WW"
"DV", "BP", "XJ", "TF", "GQ", "WH", "ZR", "MW", "HB", "NR"
"YV", "AI", "QR", "HQ", "MY", "OA", "JE", "EO", "OK", "VO"
"ZY", "XR", "EC", "UF", "KF", "LZ", "YI", "UO", "XR", "HX"
 
 

Benchmarks:

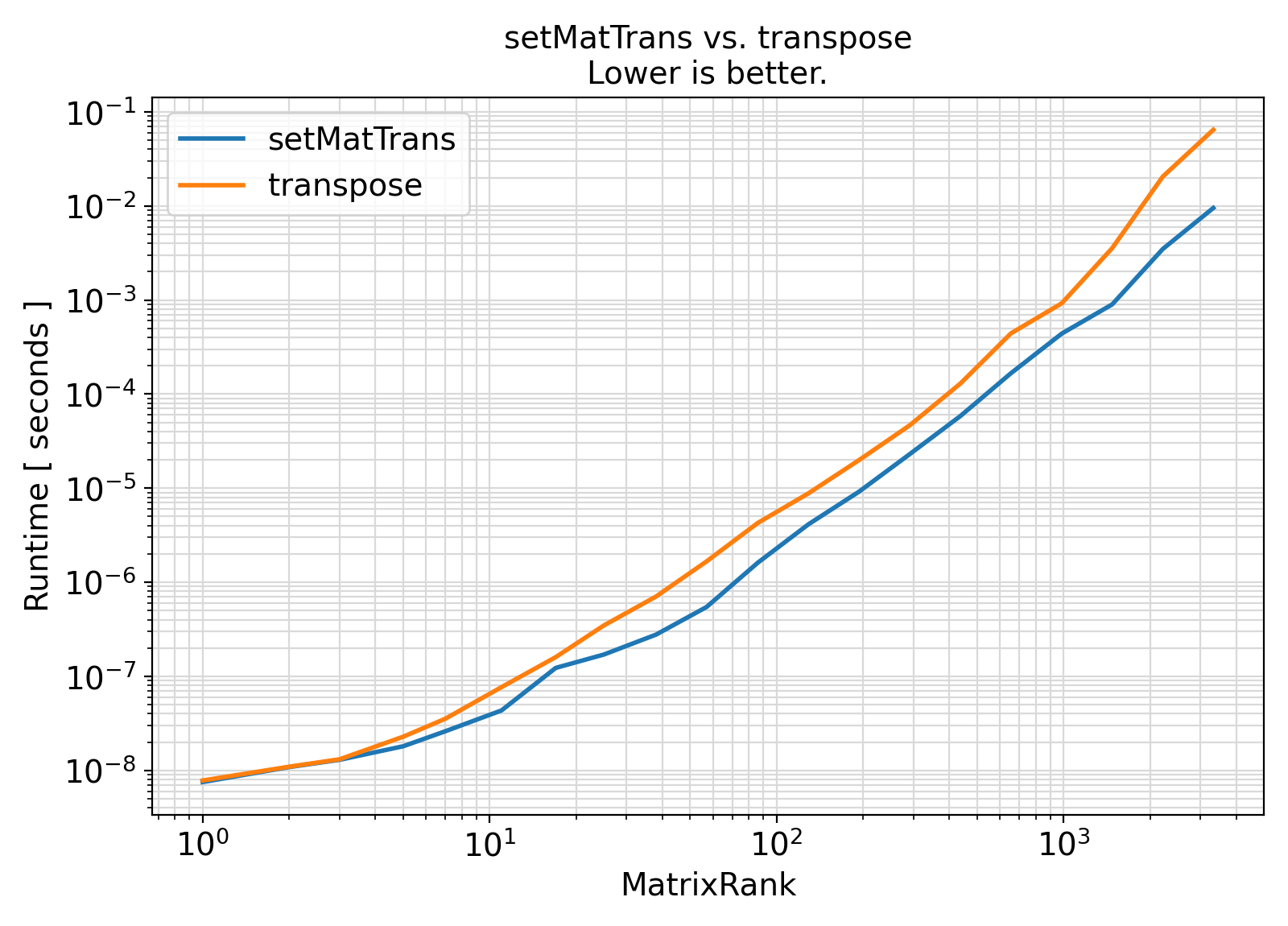
Benchmark :: The runtime performance of setMatTrans vs. Fortran intrinsic transpose(). ⛓

#define MatB_ENABLED 0
! Test the performance of `transpose()` vs. `setMatTrans()`.
program benchmark
 
    use iso_fortran_env, only: error_unit
    use pm_kind, only: IK, RKG => RK, RK, SK
    use pm_distUnif, only: setUnifRand
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i
    integer(IK)                         :: fileUnit
    integer(IK)                         :: rank, irank
    integer(IK) , parameter             :: NRANK = 20_IK
    integer(IK) , parameter             :: NBENCH = 2_IK
    real(RKG)                           :: dummySum = 0._RKG
    real(RKG)   , allocatable           :: matA(:,:)
#if MatB_ENABLED
    real(RKG)   , allocatable           :: matB(:,:)
#endif
    type(bench_type)                    :: bench(NBENCH)
 
    bench(1) = bench_type(name = SK_"setMatTrans", exec = setMatTrans , overhead = setOverhead)
    bench(2) = bench_type(name = SK_"transpose", exec = transpose , overhead = setOverhead)
 
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "setMatTrans() vs. transpose()"
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,', '))") "MatrixRank", (bench(i)%name, i = 1, NBENCH)
 
        loopOverMatrixRank: do irank = 1, NRANK
 
            rank = 1.5**irank
            allocate(matA(rank, rank)); call setUnifRand(matA)
#if         MatB_ENABLED
            allocate(matB(rank, rank)); call setUnifRand(matB)
#endif
            write(*,"(*(g0,:,' '))") "Benchmarking with rank", rank
 
            do i = 1, NBENCH
                bench(i)%timing = bench(i)%getTiming(minsec = 0.07_RK)
            end do
 
            write(fileUnit,"(*(g0,:,', '))") rank, (bench(i)%timing%mean, i = 1, NBENCH)
            deallocate(matA)
#if         MatB_ENABLED
            deallocate(matB)
#endif
        end do loopOverMatrixRank
        write(*,"(*(g0,:,' '))") dummySum
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call getDummy()
    end subroutine
 
    subroutine getDummy()
#if     MatB_ENABLED
        dummySum = dummySum + matB(1,1)
#else
        dummySum = dummySum + matA(1,1)
#endif
    end subroutine
 
    subroutine setMatTrans()
        block
            use pm_matrixTrans, only: setMatTrans
#if         MatB_ENABLED
            call setMatTrans(matA, matB)
#else
            call setMatTrans(matA)
#endif
            call getDummy()
        end block
    end subroutine
 
    subroutine transpose()
        block
            intrinsic :: transpose
#if         MatB_ENABLED
            matB = transpose(matA)
#else
            matA = transpose(matA)
#endif
            call getDummy()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ", ")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

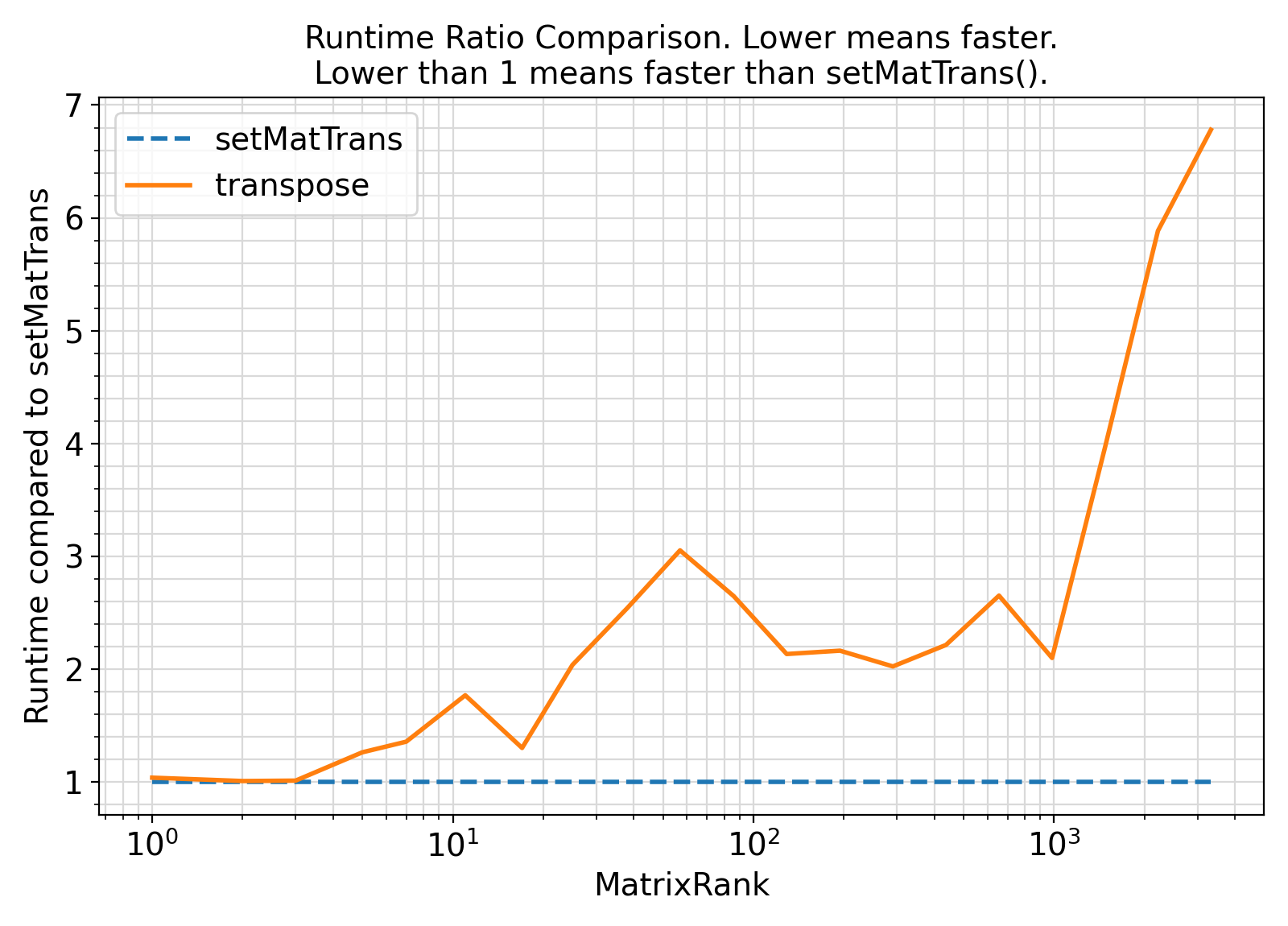
Visualization of the benchmark output ⛓

Benchmark moral ⛓

1. The procedures under the generic interface setMatTrans use a cache-oblivious approach to matrix Symmetric transposition.
   As such, they are particularly efficient and cache-friendly for large matrices.
   As such, the generic interface setMatTrans can be significantly faster than the Fortran intrinsic transpose(), depending on the Fortran compiler used.
   This is particularly true for large-order matrices.

Benchmark :: The runtime performance of setMatTrans vs. Fortran intrinsic transpose(). ⛓

! Test the performance of `transpose()` vs. `setMatTrans()`.
program benchmark
 
    use iso_fortran_env, only: error_unit
    use pm_kind, only: IK, RKG => RKS, RK, SK
    use pm_distUnif, only: setUnifRand
    use pm_bench, only: bench_type
 
    implicit none
 
    integer(IK)                         :: i
    integer(IK)                         :: fileUnit
    integer(IK)                         :: rank, irank
    integer(IK) , parameter             :: NRANK = 20_IK
    integer(IK) , parameter             :: NBENCH = 2_IK
    complex(RKG)                        :: dummySum = 0._RKG
    complex(RKG), allocatable           :: matA(:,:)
    type(bench_type)                    :: bench(NBENCH)
 
    bench(1) = bench_type(name = SK_"setMatTrans(transHerm)", exec = setMatTrans , overhead = setOverhead)
    bench(2) = bench_type(name = SK_"transpose(conjg())", exec = transpose , overhead = setOverhead)
 
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "setMatTrans() vs. transpose(conjg())"
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,', '))") "MatrixRank", (bench(i)%name, i = 1, NBENCH)
 
        loopOverMatrixRank: do irank = 1, NRANK
 
            rank = 1.5**irank
            allocate(matA(rank, rank))
            write(*,"(*(g0,:,' '))") "Benchmarking with rank", rank
            call setUnifRand(matA)
 
            do i = 1, NBENCH
                bench(i)%timing = bench(i)%getTiming(minsec = 0.07_RK)
            end do
 
            write(fileUnit,"(*(g0,:,', '))") rank, (bench(i)%timing%mean, i = 1, NBENCH)
            deallocate(matA)
 
        end do loopOverMatrixRank
        write(*,"(*(g0,:,' '))") dummySum
        write(*,"(*(g0,:,' '))")
 
    close(fileUnit)
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call getDummy()
    end subroutine
 
    subroutine getDummy()
        dummySum = dummySum + matA(1,1)
    end subroutine
 
    subroutine setMatTrans()
        block
            use pm_matrixTrans, only: setMatTrans, transHerm
            call setMatTrans(matA, operation = transHerm)
            call getDummy()
        end block
    end subroutine
 
    subroutine transpose()
        block
            intrinsic :: transpose
            matA = transpose(conjg(matA))
            call getDummy()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ", ")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

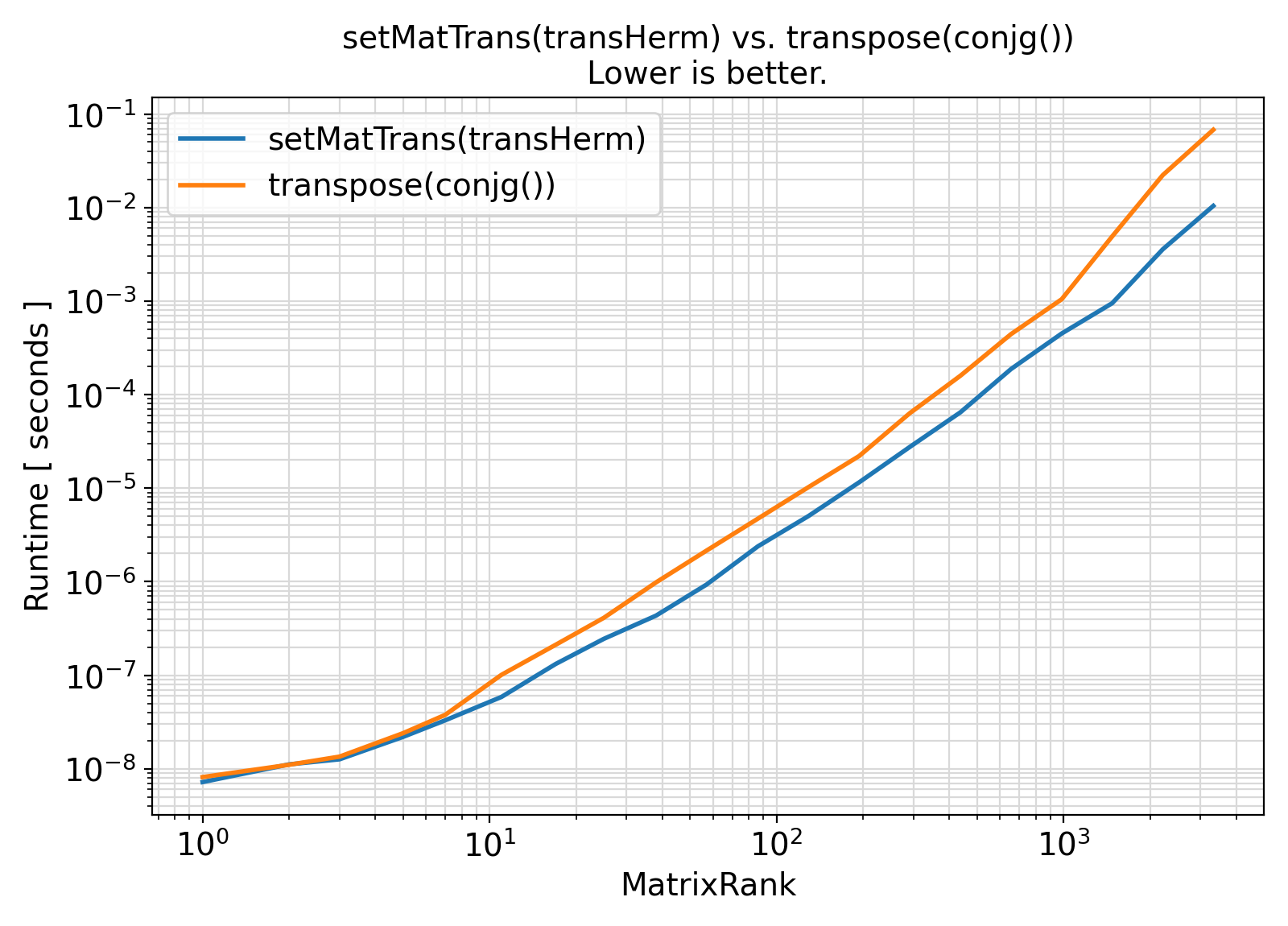
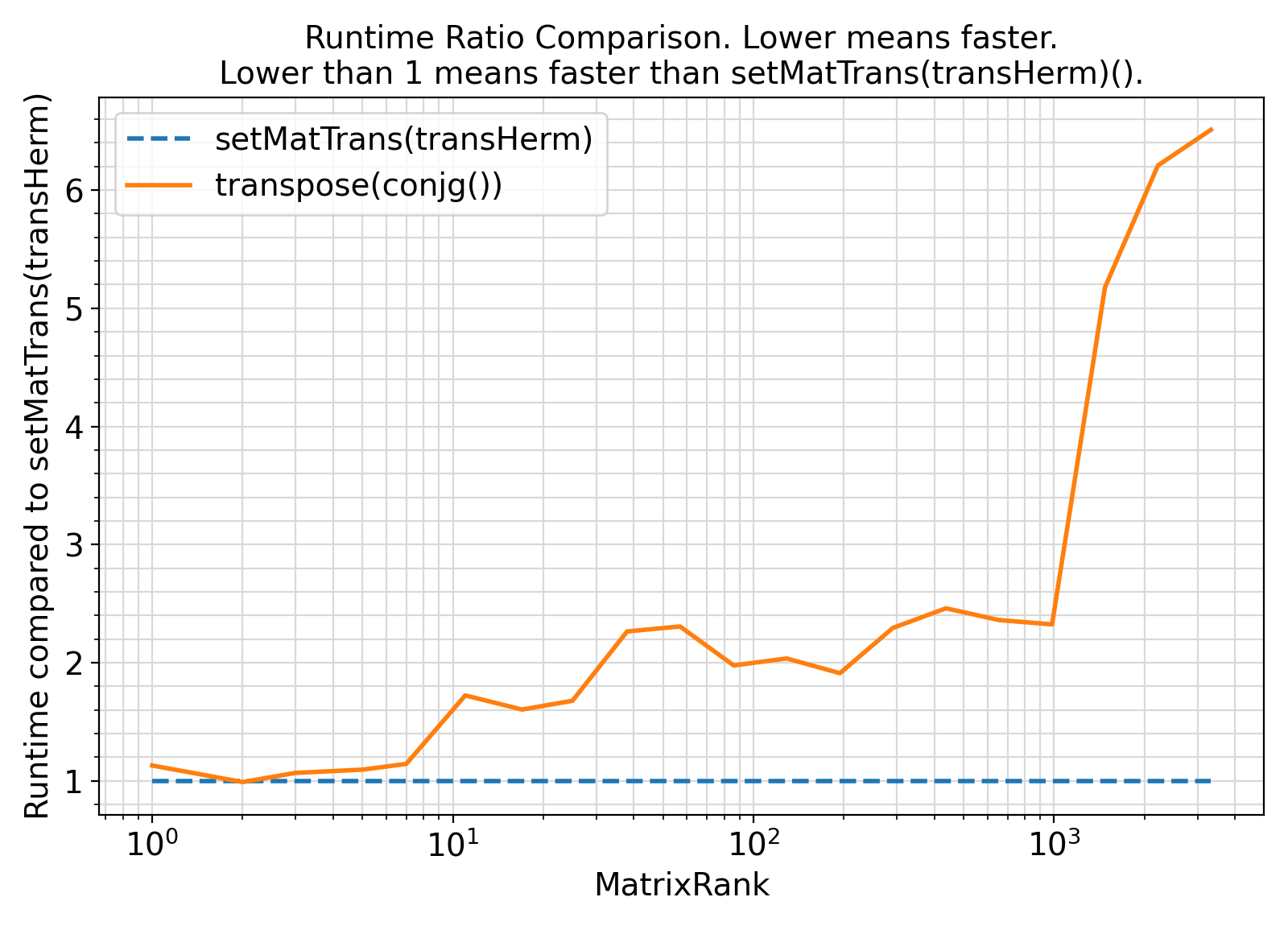
Visualization of the benchmark output ⛓

Benchmark moral ⛓

1. The procedures under the generic interface setMatTrans use a cache-oblivious approach to matrix Hermitian transposition.
   As such, they are particularly efficient and cache-friendly for large matrices.
   As such, the generic interface setMatTrans can be significantly faster than the Fortran intrinsic transpose(), depending on the Fortran compiler used.
   This is particularly true for large-order matrices.

Benchmark :: The runtime performance of setMatTrans vs. Fortran intrinsic transpose(). ⛓

#define MatB_ENABLED 0
! Test the performance of `transpose()` vs. `setMatTrans()`.
program benchmark
 
    use iso_fortran_env, only: error_unit
    use pm_kind, only: IK, RKG => RK, RK, SK
    use pm_distUnif, only: setUnifRand
    use pm_arraySpace, only: getLogSpace
    use pm_arrayReplace, only: getReplaced
    use pm_arrayUnique, only: getUnique
    use pm_bench, only: bench_type
    use pm_val2str, only: getStr
 
    implicit none
 
    integer(IK)                     :: i
    integer(IK)                     :: fileUnit
    integer(IK)                     :: iblock
    integer(IK)                     :: bsize
    integer(IK)     , parameter     :: RANK = 1000_IK
    real(RKG)                       :: dummySum = 0._RKG
    integer(IK)     , allocatable   :: BlockSize(:)
    type(bench_type), allocatable   :: bench(:)
    real(RKG)       , allocatable   :: matA(:,:)
#if MatB_ENABLED
    real(RKG)       , allocatable   :: matB(:,:)
    allocate(matB(RANK, RANK))
    call setUnifRand(matB)
#endif
    allocate(matA(RANK, RANK))
    call setUnifRand(matA)
 
    bench = [ bench_type(name = getReplaced(SK_"setMatTrans(matA(RANK,RANK))", SK_"RANK", getStr(RANK)), exec = setMatTrans, overhead = setOverhead) &
            , bench_type(name = getReplaced(  SK_"transpose(matA(RANK,RANK))", SK_"RANK", getStr(RANK)), exec = transpose, overhead = setOverhead) &
            ]
 
    BlockSize = getUnique(int(getLogSpace(log(1._RKG), log(real(2*RANK, RKG)), count = 50_IK), IK))
 
    write(*,"(*(g0,:,' '))")
    write(*,"(*(g0,:,' '))") "setMatTransBlock"
    write(*,"(*(g0,:,' '))")
 
    open(newunit = fileUnit, file = "main.out", status = "replace")
 
        write(fileUnit, "(*(g0,:,', '))") "BlockSize", (bench(i)%name, i = 1, size(bench))
 
        loopOverMatrixRank: do iblock = 1, size(BlockSize)
 
            bsize = BlockSize(iblock)
            write(*,"(*(g0,:,' '))") "Benchmarking with block size", bsize
 
            do i = 1, size(bench)
                bench(i)%timing = bench(i)%getTiming(minsec = 0.07_RK)
            end do
 
            write(fileUnit,"(*(g0,:,', '))") bsize, (bench(i)%timing%mean, i = 1, size(bench))
 
        end do loopOverMatrixRank
 
    close(fileUnit)
 
    write(*,"(*(g0,:,' '))") dummySum
    write(*,"(*(g0,:,' '))")
 
contains
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! procedure wrappers.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    subroutine setOverhead()
        call getDummy()
    end subroutine
 
    subroutine getDummy()
#if     MatB_ENABLED
        dummySum = dummySum + matB(1,1)
#else
        dummySum = dummySum + matA(1,1)
#endif
    end subroutine
 
    subroutine setMatTrans()
        block
            use pm_matrixTrans, only: setMatTrans
#if         MatB_ENABLED
            call setMatTrans(matA, matB, bsize)
#else
            call setMatTrans(matA, bsize)
#endif
            call getDummy()
        end block
    end subroutine
 
    subroutine transpose()
        block
            intrinsic :: transpose
#if         MatB_ENABLED
            matB = transpose(matA)
#else
            matA = transpose(matA)
#endif
            call getDummy()
        end block
    end subroutine
 
end program benchmark

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Postprocessing of the benchmark output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
 
import os
dirname = os.path.basename(os.getcwd()) 
 
fontsize = 14
 
df = pd.read_csv("main.out", delimiter = ", ")
colnames = list(df.columns.values)
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
for colname in colnames[1:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime [ seconds ]", fontsize = fontsize)
ax.set_title(" vs. ".join(colnames[1:])+"\nLower is better.", fontsize = fontsize)
ax.set_xscale("log")
ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, loc='center left'
           #, bbox_to_anchor=(1, 0.5)
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.png")
 
 
 
ax = plt.figure(figsize = 1.25 * np.array([6.4,4.6]), dpi = 200)
ax = plt.subplot()
 
plt.plot( df[colnames[0]].values
        , np.ones(len(df[colnames[0]].values))
        , linestyle = "--"
       #, color = "black"
        , linewidth = 2
        )
for colname in colnames[2:]:
    plt.plot( df[colnames[0]].values
            , df[colname].values / df[colnames[1]].values
            , linewidth = 2
            )
 
plt.xticks(fontsize = fontsize)
plt.yticks(fontsize = fontsize)
ax.set_xlabel(colnames[0], fontsize = fontsize)
ax.set_ylabel("Runtime compared to {}".format(colnames[1]), fontsize = fontsize)
ax.set_title("Runtime Ratio Comparison. Lower means faster.\nLower than 1 means faster than {}().".format(colnames[1]), fontsize = fontsize)
ax.set_xscale("log")
#ax.set_yscale("log")
plt.minorticks_on()
plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
ax.tick_params(axis = "y", which = "minor")
ax.tick_params(axis = "x", which = "minor")
ax.legend   ( colnames[1:]
           #, bbox_to_anchor = (1, 0.5)
           #, loc = "center left"
            , fontsize = fontsize
            )
 
plt.tight_layout()
plt.savefig("benchmark." + dirname + ".runtime.ratio.png")

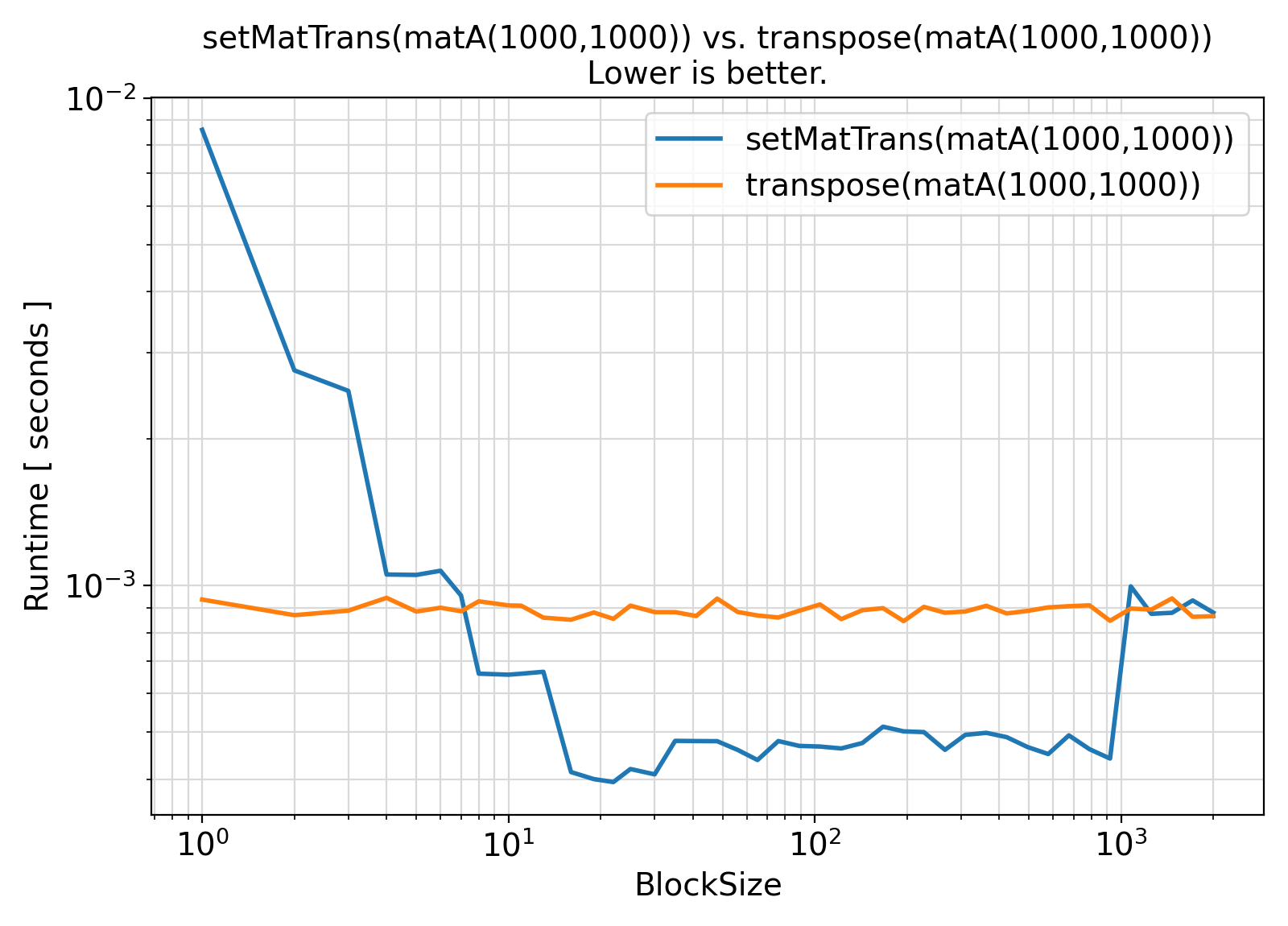
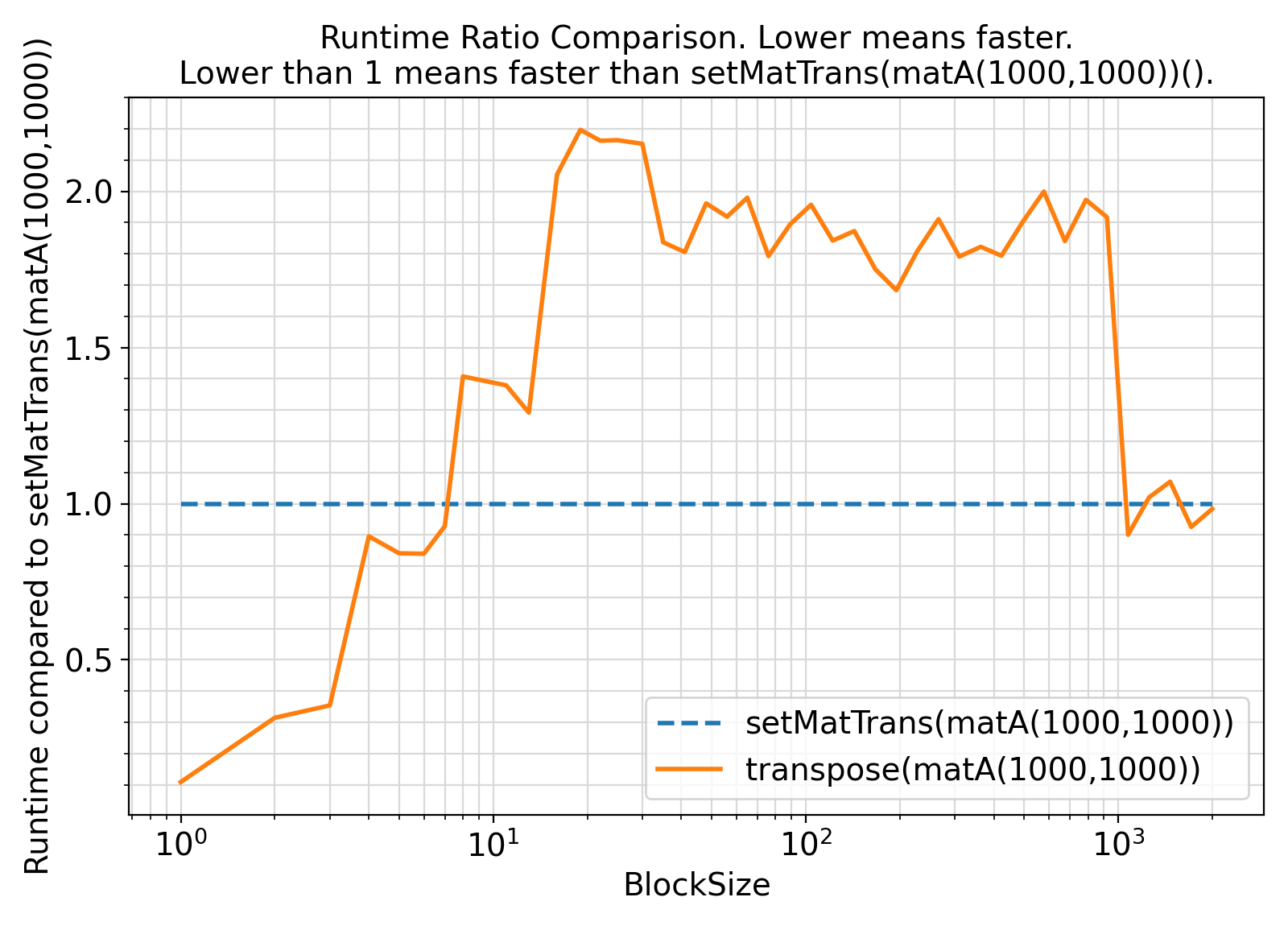
Visualization of the benchmark output ⛓

Benchmark moral ⛓

1. The procedures under the generic interface setMatTrans use a cache-oblivious approach to matrix Hermitian transposition.
   As such, they are particularly efficient and cache-friendly for large matrices.
   However, despite its name and goals, the cache-oblivious algorithm is not entirely independent of the cache size (and hence the minimum block size) as evidenced here.
   

Test:

test_pm_matrixTrans

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Todo:

Normal Priority: The performance of this algorithm could be possibly improved by converting the recursive procedure calls within the implementation to do-loops.

Author:

Amir Shahmoradi, September 1, 2017, 12:00 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 767 of file pm_matrixTrans.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_matrixTrans.F90