pm_mathFactorial::getLogFactorial Interface Reference

Generate and return the natural logarithm of the factorial of the input positive whole real number. More...

Detailed Description

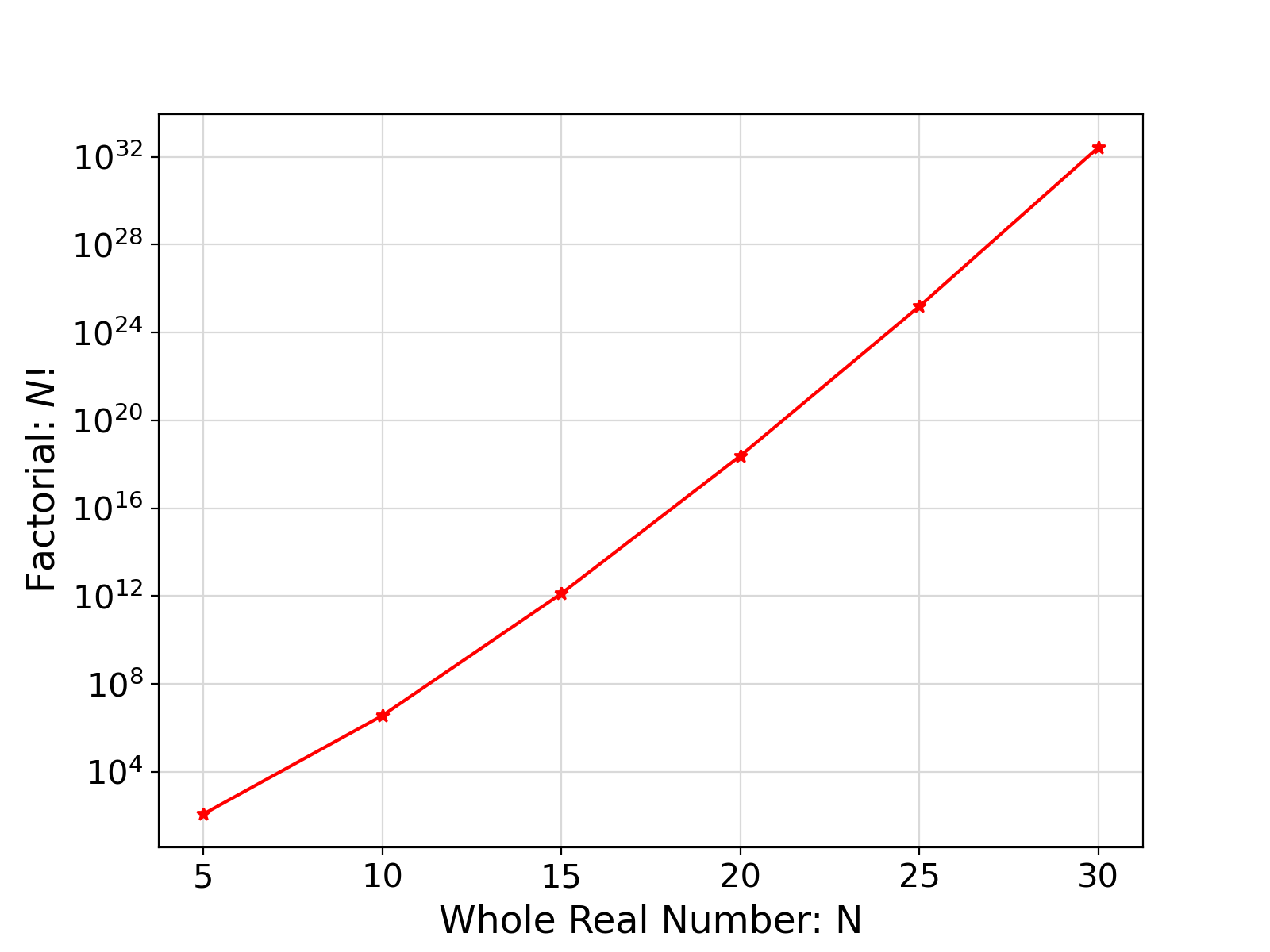
Generate and return the natural logarithm of the factorial of the input positive whole real number.

The factorial of an integer number \(n\) is defined as,

\begin{equation} \large n! = \prod_{i=1}^{n} i = \Gamma(n+1) ~. \end{equation}

Therefore,

\begin{equation} \large \log(n!) = \sum_{i=1}^{n} i = \log\bigg(\Gamma(n+1)\bigg) ~. \end{equation}

Note that the factorial of a number can readily overflow the maximum integer or even real values representable by computers. This is the primary reason for computing the natural logarithm of the factorial instead of the factorial.

Parameters

[in]

x

: The input scalar or array of arbitrary rank of type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128) containing the whole number (integer) whose \(\log(x!)\) is to be computed on return.

Returns

logFactorial : The output scalar or array of the same shape as the input x representing the natural logarithm of the factorial of x.

Possible calling interfaces ⛓

use pm_mathFactorial, only: getLogFactorial
 
logFactorial = getLogFactorial(x)

Warning

The input x must be a positive whole number.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

Remarks

The procedures under discussion are elemental.

See also

getFactorial

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK, LK
    use pm_kind, only: RKS, RKD, RKH
    use pm_io, only: display_type
    use pm_mathFactorial, only: getLogFactorial
 
    implicit none
 
    integer(IK) , parameter :: NP = 1000_IK
    real(RKH)               :: gamIncLow_RKH, x_RKH, shape_RKH
    real(RKD)               :: gamIncLow_RKD, x_RKD, shape_RKD
    real(RKS)               :: gamIncLow_RKS, x_RKS, shape_RKS
    logical(LK)             :: failed
 
    type(display_type) :: disp
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("exp(getLogFactorial(x = 3._RKS))")
    call disp%show( exp(getLogFactorial(x = 3._RKS)) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("exp(getLogFactorial(x = 4._RKD))")
    call disp%show( exp(getLogFactorial(x = 4._RKD)) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("exp(getLogFactorial(x = 5._RKH))")
    call disp%show( exp(getLogFactorial(x = 5._RKH)) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("exp(getLogFactorial(x = real([3., 5., 7., 10.],RKS)))")
    call disp%show( exp(getLogFactorial(x = real([3., 5., 7., 10.],RKS))) )
    call disp%skip()
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! Output an example array of the regularized Lower Incomplete Gamma function for visualization.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    block
 
        use pm_arrayRange, only: getRange
        real(RKS), allocatable :: WholeNumber(:)
        integer :: fileUnit, i
 
        WholeNumber = getRange(start = 0_IK, stop = 30_IK, step = 5_IK)
        open(newunit = fileUnit, file = "getLogFactorial.RK.txt")
        write(fileUnit,"(2(g0,:,' '))") (WholeNumber(i), exp(getLogFactorial(WholeNumber(i))), i = 1, size(WholeNumber))
        close(fileUnit)
 
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
exp(getLogFactorial(x = 3._RKS))
+6.00000000
 
 
exp(getLogFactorial(x = 4._RKD))
+24.000000000000004
 
 
exp(getLogFactorial(x = 5._RKH))
+119.999999999999999999999999999999963
 
 
exp(getLogFactorial(x = real([3., 5., 7., 10.],RKS)))
+6.00000000, +120.000008, +5040.00195, +3628801.75
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
fontsize = 17
 
marker ={ "CK" : "*"
        , "IK" : "*"
        , "RK" : "*"
        }
linestyle = { "CK" : "-"
            , "IK" : "-"
            , "RK" : "-"
            }
xlab =  { "CK" : r"Whole Complex Number: N"
        , "IK" : r"Whole Integer Number: N"
        , "RK" : r"Whole Real Number: N"
        }
 
for kind in ["IK", "CK", "RK"]:
 
    pattern = "*." + kind + ".txt"
    fileList = glob.glob(pattern)
    if len(fileList) == 1:
 
        df = pd.read_csv(fileList[0], delimiter = " ")
 
        fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
        ax = plt.subplot()
 
        if kind == "CK":
            plt.plot( df.values[:, 0]
                    , df.values[:,2]
                    , marker = marker[kind]
                    , linestyle = linestyle[kind]
                    , color = "r"
                    )
            plt.plot( df.values[:, 1]
                    , df.values[:,3]
                    , marker = marker[kind]
                    , linestyle = linestyle[kind]
                    , color = "blue"
                    )
        else:
            plt.plot( df.values[:, 0]
                    , df.values[:, 1]
                    , marker = marker[kind]
                    , linestyle = linestyle[kind]
                    , color = "r"
                    )
 
        plt.xticks(fontsize = fontsize - 2)
        plt.yticks(fontsize = fontsize - 2)
        ax.set_xlabel(xlab[kind], fontsize = fontsize)
        ax.set_ylabel(r"Factorial: $N!$", fontsize = fontsize)
        ax.set_yscale("log")
 
        plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
        ax.tick_params(axis = "y", which = "minor")
        ax.tick_params(axis = "x", which = "minor")
 
        plt.savefig(fileList[0].replace(".txt",".png"))
 
    elif len(fileList) > 1:
 
        sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:

test_pm_mathFactorial

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, April 23, 2017, 1:36 AM, Institute for Computational Engineering and Sciences (ICES), University of Texas at Austin

Definition at line 244 of file pm_mathFactorial.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_mathFactorial.F90