pm_cosmology::getDisLookbackNormed Interface Reference

Generate and return the cosmological Lookback Distance (or equivalently, the Lookback Time) at the desired redshift normalized to Hubble Distance (or equivalently, to Hubble Time), given the user-specified cosmological parameters. More...

Detailed Description

Generate and return the cosmological Lookback Distance (or equivalently, the Lookback Time) at the desired redshift normalized to Hubble Distance (or equivalently, to Hubble Time), given the user-specified cosmological parameters.

Assuming \((\Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)\) represent the normalized densities of Dark Matter, Dark Energy, Radiation Energy, and Curvature in a Universe with negligible neutrino mass such that \(\Omega_M + \Omega_\Lambda + \Omega_R + \Omega_K = 1\), the Lookback Distance to a cosmological object as redshift \(z\) is simply related to the Hubble Parameter as,

\begin{equation} \large D_T(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = D_H \int_{0}^{z} \frac{1}{(1+z') E(z'; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)} ~ dz' ~, \end{equation}

or equivalently, the Lookback Time to a cosmological object as redshift \(z\) is simply related to the Hubble Parameter as,

\begin{equation} \large T_L(z; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K) = T_H \int_{0}^{z} \frac{1}{(1+z') E(z'; \Omega_M, \Omega_\Lambda, \Omega_R, \Omega_K)} ~ dz' ~, \end{equation}

where,

1. \(z\) is the redshift,
2. \(D_T\) is the cosmological Lookback Distance,
3. \(T_L\) is the cosmological Lookback Time,
4. \(E(z; \cdots)\) is the dimensionless Hubble Parameter,
5. \(D_H = \frac{C}{H_0}\) is the Hubble Distance,
6. \(T_H = \frac{1}{H_0}\) is the Hubble Time,
7. \(H_0\) is the Hubble Constant.
8. \(C\) is the speed of light,

The Lookback Distance, also known as the Light-Travel Distance, is defined as the distance traveled by light from the given redshift to Earth.
Dividing the Lookback Distance by the Speed of Light yields the Lookback Time.
For instance, the radius of the observable universe in this distance measure becomes the age of the universe multiplied by the speed of light (1 light year/year), which turns out to be approximately 13.8 billion light years.

The value returned by the procedures under this generic interface is \(\frac{D_T}{D_H}\).
The value returned by the procedures under this generic interface is \(\frac{T_L}{T_H}\).
The default method of computing the Lookback Distance is numerical integration via Adaptive Global Gauss-Kronrod 10-21 Quadrature rule.

Parameters

[in]	zplus1	: The input scalar or array of the same rank as other array-like arguments, of type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128) representing the redshift plus one, \(\log(z+1)\), at which the Lookback Distance must be computed.
[in]	omegaM	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized matter density in the universe. (optional, default = OMEGA_M. It must be present if omegaL ( \(\Omega_\Lambda\)) is also present.)
[in]	omegaL	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized Dark Energy density in the universe. (optional, default = OMEGA_L. It must be present if omegaR is also present.)
[in]	omegaR	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized radiation density in the universe. (optional, default = OMEGA_R. It must be present if omegaK is also present.)
[in]	omegaK	: The input scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 representing the normalized curvature density of the universe. (optional, default = OMEGA_K)
[in]	reltol	: See the description of the corresponding argument in the documentation of getQuadErr. A reasonable recommended value is reltol = sqrt(epsilon(real(0, kind(zplus1)))).
[out]	neval	: See the description of the corresponding argument in the documentation of getQuadErr. (optional. If missing, the number of function evaluations will not be returned.)
[out]	err	: The output scalar of type integer of default kind IK, that is set to zero if the integration converges without any errors. Otherwise, a non-zero value of err indicates the occurrence of an error of varying severities. See the description of the corresponding output argument in the documentation of getQuadErr.

Returns

disLookbackNormed : The output scalar or array of the same rank as other array-like arguments, of the same type and kind as the input argument zplus1 containing the cosmological Lookback Distance (or Lookback Time) at the desired redshift normalized to the Hubble Distance (or Hubble Time).

Possible calling interfaces ⛓

use pm_cosmology, only: getDisLookbackNormed
 
disLookbackNormed = getDisLookbackNormed(zplus1, reltol, neval = neval, err = err)
disLookbackNormed = getDisLookbackNormed(zplus1, omegaM, omegaL, reltol, neval = neval, err = err)
disLookbackNormed = getDisLookbackNormed(zplus1, omegaM, omegaL, omegaR, reltol, neval = neval, err = err)
disLookbackNormed = getDisLookbackNormed(zplus1, omegaM, omegaL, omegaR, omegaK, sqrtAbsOmegaK, reltol, neval = neval, err = err)

Warning

The conditions listed in the documentation of getDisComTransNormed must hold for this generic interface.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

Remarks

The procedures under discussion are impure.

The procedures under discussion are elemental.

Note

Dropping all optional arguments corresponds to the \(\Lambda\)CDM Universe with the latest experimental parameter inferences.

Setting omegaM = 1 and omegaL = 0 corresponds to the Einstein–de Sitter model of the universe proposed by Albert Einstein and Willem de Sitter in 1932.

See also

getHubbleParamNormedSq
getDisComTransNormed
getDisLookbackNormed
getDisAngNormed
getDisLumNormed
getDisComNormed
LOG_HUBBLE_CONST
HUBBLE_DISTANCE_MPC
HUBBLE_CONST
OMEGA_M
OMEGA_L
OMEGA_R
OMEGA_K

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK
    use pm_cosmology, only: HUBBLE_DISTANCE_GLY
    use pm_cosmology, only: getDisLookbackNormed
    use pm_io, only: display_type
 
    implicit none
 
    type(display_type)      :: disp
 
    disp = display_type(file = "main.out.F90")
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!Compute the Comoving diameter distance in units of Hubble Distance.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisLookbackNormed(zplus1 = 1., reltol = sqrt(epsilon(0.)))")
    call disp%show( getDisLookbackNormed(zplus1 = 1., reltol = sqrt(epsilon(0.))) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisLookbackNormed(zplus1 = 1.1, reltol = sqrt(epsilon(0.)))")
    call disp%show( getDisLookbackNormed(zplus1 = 1.1, reltol = sqrt(epsilon(0.))) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6, reltol = 0.0001)")
    call disp%show( getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6, reltol = 0.0001) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.4, omegaR = 0.2, reltol = 0.0001)")
    call disp%show( getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.4, omegaR = 0.2, reltol = 0.0001) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.4, omegaR = 0.4, omegaK = -0.2, reltol = 0.0001)")
    call disp%show( getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.4, omegaR = 0.4, omegaK = -0.2, reltol = 0.0001) )
    call disp%skip()
 
    ! Generate both the cosmic rate and the rate density.
 
    block
 
        use pm_val2str, only: getStr
        use pm_arraySpace, only: getLinSpace
        use pm_arraySpace, only: getLogSpace
 
        real, allocatable   :: zplus1(:), OmegaM(:), OmegaL(:)
        integer :: fileUnit, i
 
        OmegaM = [0., 0.5, 1.]
        OmegaL = 1. - OmegaM
        zplus1 = 1. + getLogSpace(log(0.0001), log(10000.), 500_IK)
 
        open(newunit = fileUnit, file = "getDisLookbackNormed.RK.txt")
        write(fileUnit, "(*(g0,:,','))") "z", ("DisLum_"//getStr(OmegaM(i),"(g0.1)")//"_"//getStr(OmegaL(i),"(g0.1)"), i = 1, size(OmegaM))
        do i = 1, size(zplus1)
            write(fileUnit, "(*(g0,:,','))") zplus1(i) - 1., HUBBLE_DISTANCE_GLY * getDisLookbackNormed(zplus1(i), OmegaM, OmegaL, sqrt(epsilon(0.)))
        end do
        close(fileUnit)
 
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!Compute the Comoving diameter distance in units of Hubble Distance.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
getDisLookbackNormed(zplus1 = 1., reltol = sqrt(epsilon(0.)))
+0.00000000
 
 
getDisLookbackNormed(zplus1 = 1.1, reltol = sqrt(epsilon(0.)))
+0.930913836E-1
 
 
getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.6, reltol = 0.0001)
+0.526044846, +0.686934590
 
 
getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.4, omegaR = 0.2, reltol = 0.0001)
+0.462942034, +0.575396061
 
 
getDisLookbackNormed(zplus1 = [ 2., 3.], omegaM = 0.4, omegaL = 0.4, omegaR = 0.4, omegaK = -0.2, reltol = 0.0001)
+0.433974087, +0.527949393
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
fontsize = 17
 
marker ={ "CK" : "-"
        , "IK" : "."
        , "RK" : "-"
        }
xlab =  { "CK" : "redshift: Z ( real/imaginary components )"
        , "IK" : "redshift: Z ( integer-valued )"
        , "RK" : "redshift: Z ( real-valued )"
        }
legends =   [ "$\Omega_M = 0.0, \Omega_\Lambda = 1.0$"
            , "$\Omega_M = 0.5, \Omega_\Lambda = 0.5$"
            , "$\Omega_M = 1.0, \Omega_\Lambda = 0.0$"
            ]
 
for kind in ["IK", "CK", "RK"]:
 
    pattern = "*." + kind + ".txt"
    fileList = glob.glob(pattern)
    if len(fileList) == 1:
 
        df = pd.read_csv(fileList[0], delimiter = ",")
 
        fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
        ax = plt.subplot()
 
        if kind == "CK":
            plt.plot( df.values[:, 0]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "r"
                    )
            plt.plot( df.values[:, 1]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "blue"
                    )
        else:
            plt.plot( df.values[:, 0]
                    , df.values[:,1:len(legends)+1]
                    , marker[kind]
                   #, color = "r"
                    )
            ax.legend   ( legends
                        , fontsize = fontsize
                        )
 
        plt.xticks(fontsize = fontsize - 2)
        plt.yticks(fontsize = fontsize - 2)
        ax.set_xlabel(xlab[kind], fontsize = 17)
        ax.set_ylabel("Lookback Distance [ GLY ]", fontsize = 17)
        plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
        ax.tick_params(axis = "y", which = "minor")
        ax.tick_params(axis = "x", which = "minor")
        ax.set_xscale("log")
        ax.set_yscale("log")
 
        plt.tight_layout()
        plt.savefig(fileList[0].replace(".txt",".png"))
 
    elif len(fileList) > 1:
 
        sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:

test_pm_cosmology

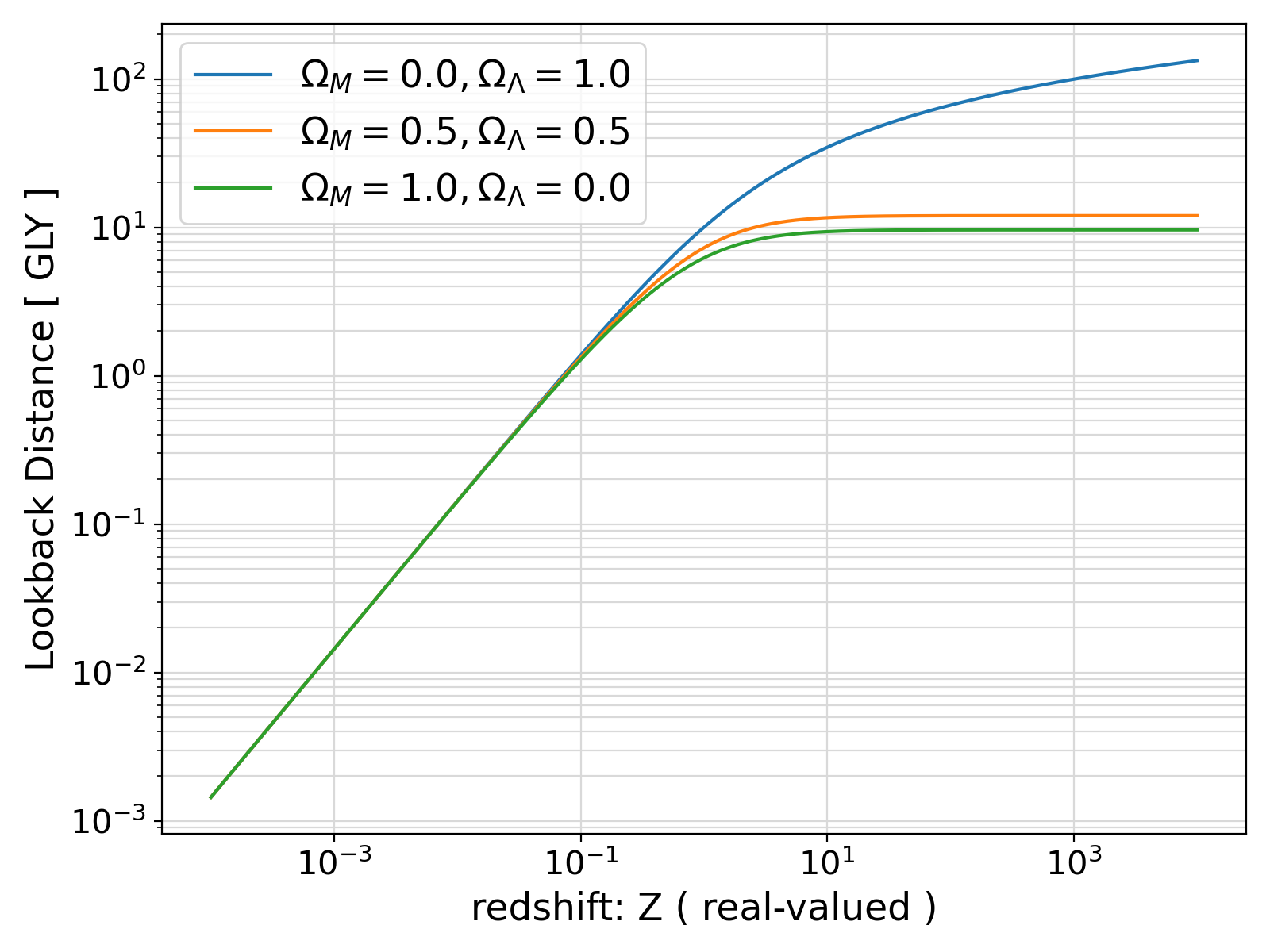
Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, September 1, 2017, 12:00 AM, Institute for Computational Engineering and Sciences (ICES), The University of Texas Austin

Definition at line 698 of file pm_cosmology.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_cosmology.F90