|
ParaMonte MATLAB 3.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
|
ParaMonte MATLAB 3.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
Go to the source code of this file.
Functions | |
| function | kde2d (in data, in resol, in xymin, in xymax) |
| Compute the Gaussian kernel density estimate of the input bivariate data. More... | |
| function kde2d | ( | in | data, |
| in | resol, | ||
| in | xymin, | ||
| in | xymax | ||
| ) |
Compute the Gaussian kernel density estimate of the input bivariate data.
This function offers a fast and accurate bivariate kernel density estimator with diagonal bandwidth matrix.
The kernel is assumed to be Gaussian.
The two bandwidth parameters are chosen optimally without ever using/assuming a parametric model for the data or any rules of thumb.
Particularly, this algorithm is immune to accuracy failures in the estimation of multimodal densities with widely separated modes (see examples below).
| [in] | data | : The input matrix of shape [nobs, 2] containing the continuous data whose density estimate is to be returned. |
| [in] | resol | : The input scalar whole number representing the size of the resol by resol grid over which the density is computed where resol has to be a power of 2, otherwise resol = 2 ^ ceil(log2(resol)) will be used.(optional. If missing or empty, it will be set to 2^8.) |
| [in] | xymin | : The input vector of size 2 containing the lower limits of the bounding box over which the density is computed.(optional. If missing or empty, it will be set to an appropriate value as prescribed in the note below.) |
| [in] | xymax | : The input vector of size 2 containing the upper limits of the bounding box over which the density is computed.(optional. If missing or empty, it will be set to an appropriate value as prescribed in the note below.) |
bandwidth : The output row vector with the two optimal bandwidths for a bivaroate Gaussian kernel.bandwidth = [bandwidth_x, bandwidth_y].density : The output resol by resol matrix containing the density values over the resol by resol grid.meshx : The x-axis meshgrid over which the variable "density" has been computed.surf.surf(meshx, meshy, density).meshy : The y-axis meshgrid over which the variable "density" has been computed.surf.surf(meshx, meshy, density).
Possible calling interfaces ⛓
xymin and xymax are as follows:
Example usage ⛓
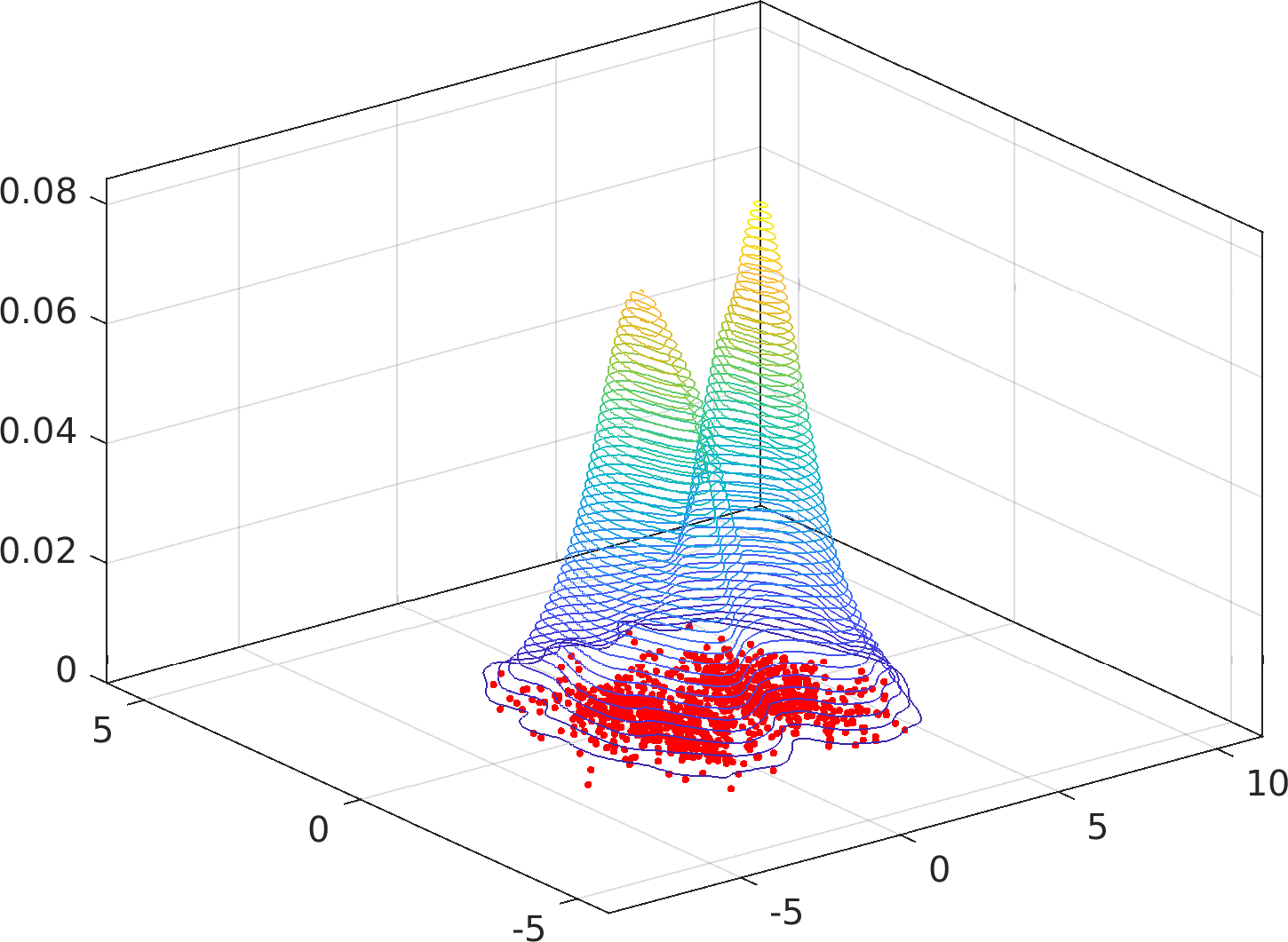
Example usage ⛓
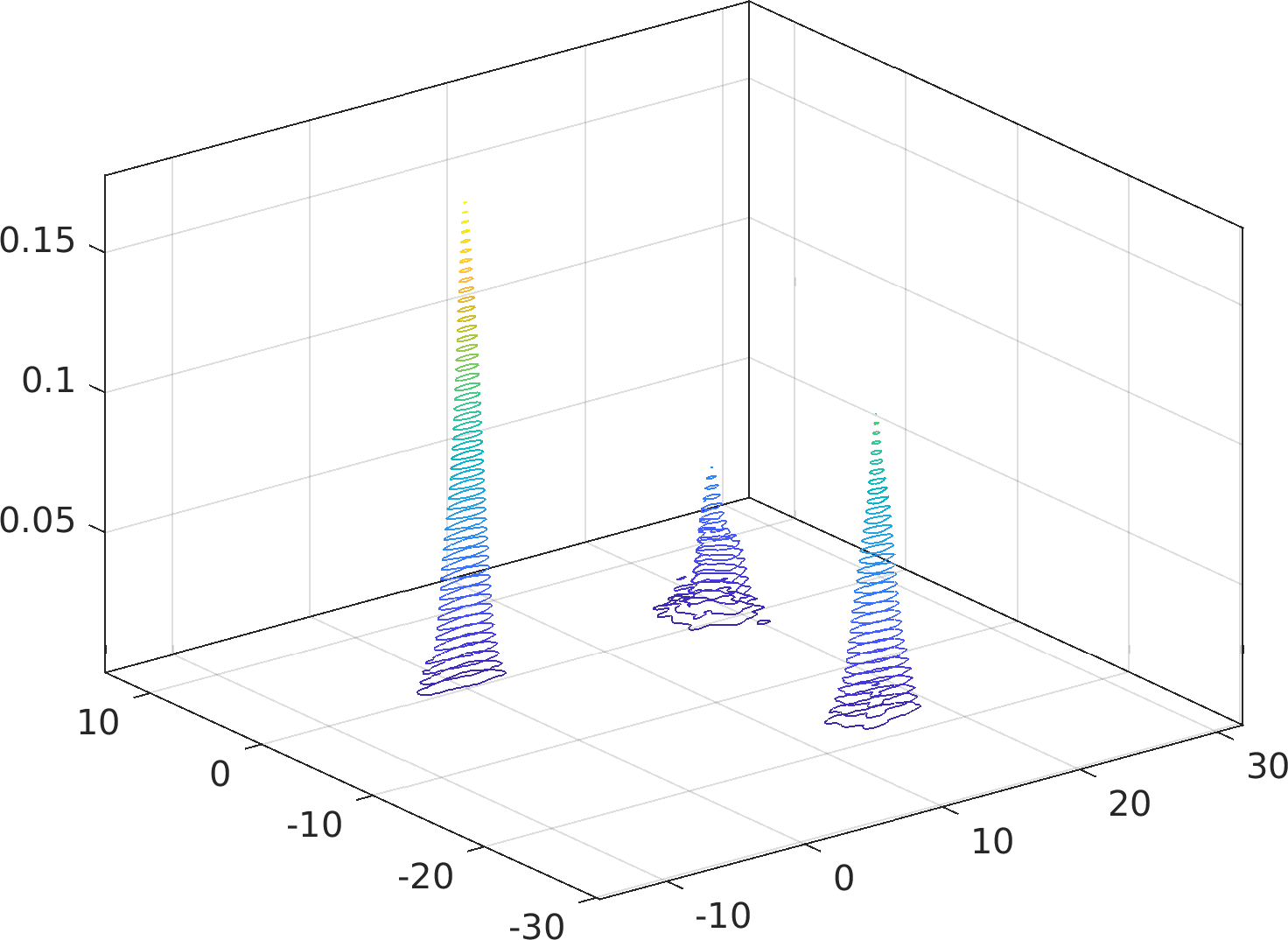
Example usage ⛓
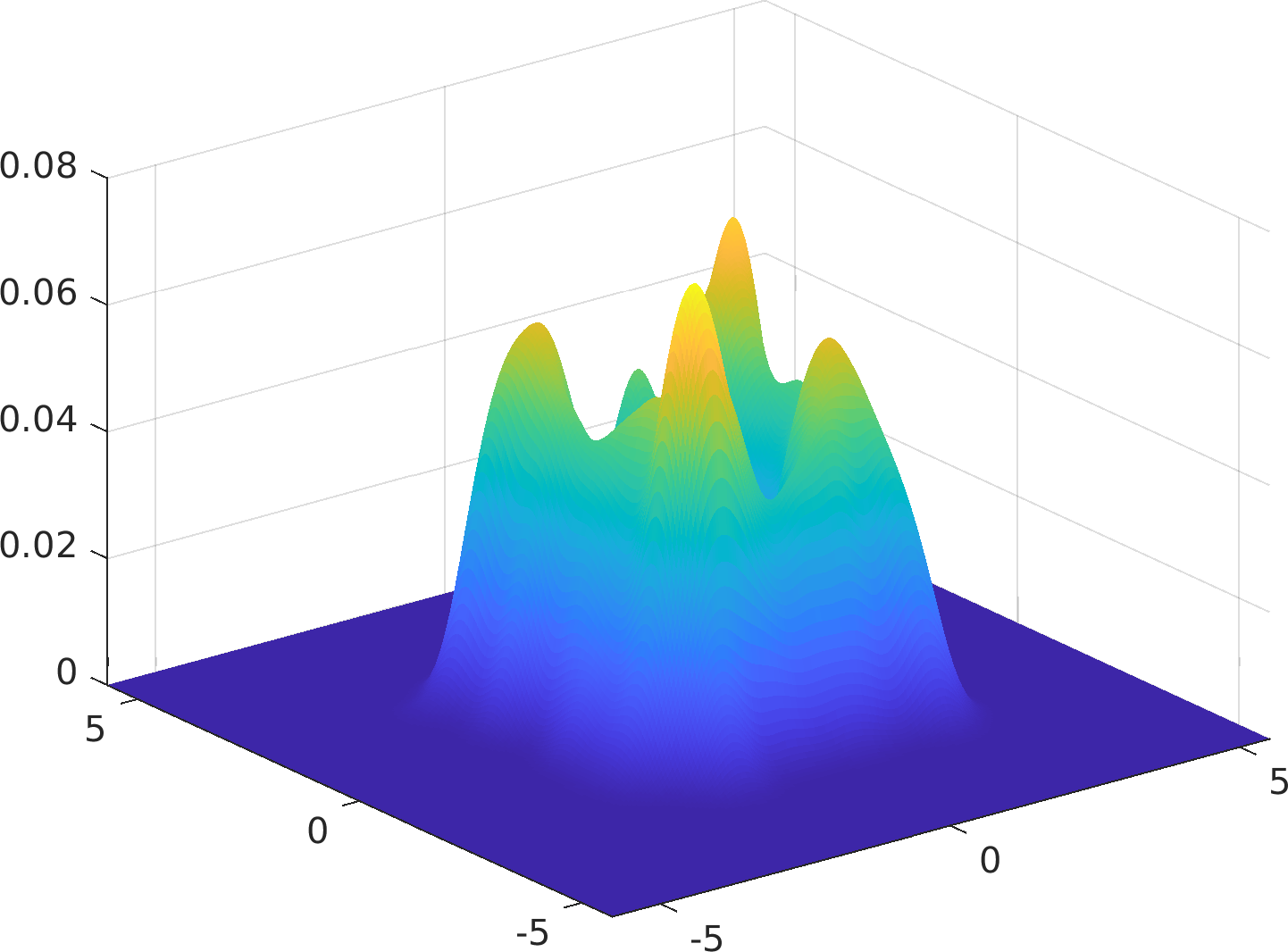
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Copyright (c) 2015, Dr. Zdravko Botev All rights reserved.
Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:
This software is provided by the copyright holders and contributors "as is" and any express or implied warranties, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose are disclaimed. In no event shall the copyright owner or contributors be liable for any direct, indirect, incidental, special, exemplary, or consequential damages (including, but not limited to, procurement of substitute goods or services; loss of use, data, or profits; or business interruption) however caused and on any theory of liability, whether in contract, strict liability, or tort (including negligence or otherwise) arising in any way out of the use of this software, even if advised of the possibility of such damage.
Amir Shahmoradi, May 16 2016, 9:03 AM, Oden Institute for Computational Engineering and Sciences (ICES), UT Austin