ParaMonte MATLAB 3.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation.
Public Member Functions
Paradram Class Reference

This is the ParaDRAM class for generating instances of serial and parallel Delayed-Rejection Adaptive Metropolis-Hastings Markov Chain Monte Carlo sampler of the ParaMonte MATLAB library.
More...

Inheritance diagram for Paradram:
Inheritance graph
[legend]
Collaboration diagram for Paradram:
Collaboration graph
[legend]

Public Member Functions

function Paradram ()
 Generate and return an instance of the serial and parallel Delayed-Rejection Adaptive Metropolis-Hastings Markov Chain Monte Carlo sampler of the ParaMonte MATLAB library.
More...
 
function getppm (in self)
 Generate and return the relevant Post-Processing Message (ppm) for the current ParaMonte sampler to be displayed on the MATLAB command line after the sampling is complete.
More...
 
function readChainMarkov (in self, in pattern, in sep)
 Return a list of objects of class pm.sampling.FileContentsChainDRAM containing the content(s) of the ParaMonte simulation output chain file(s) whose path(s) match the specified input pattern or the simulation specification sampler.spec.outputFileName.
More...
 
function run (in self, in getLogFunc, in ndim)
 Run the ParaDRAM sampler and return nothing. More...
 

Detailed Description

This is the ParaDRAM class for generating instances of serial and parallel Delayed-Rejection Adaptive Metropolis-Hastings Markov Chain Monte Carlo sampler of the ParaMonte MATLAB library.

For more information, see the documentation of the class constructor pm.sampling.Paradram::Paradram.

Note
See the documentation of the class constructor for usage interface and examples.


Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Amir Shahmoradi, May 16 2016, 9:03 AM, Oden Institute for Computational Engineering and Sciences (ICES), UT Austin

Definition at line 17 of file Paradram.m.

Constructor & Destructor Documentation

◆ Paradram()

function Paradram::Paradram ( )

Generate and return an instance of the serial and parallel Delayed-Rejection Adaptive Metropolis-Hastings Markov Chain Monte Carlo sampler of the ParaMonte MATLAB library.

This function is the constructor of the pm.sampling.Paradram sampler class.
Once you assign the desired simulation specifications to the corresponding attributes within the component spec of an object of class pm.sampling.Paradram, call the ParaDRAM sampler via the object method pm.sampling.Paradram.run().

While the constructor of this class does not take any input arguments, all ParaDRAM simulation specifications can be set after creating the object.

Returns
sampler : The output scalar object of class pm.sampling.Paradram.


Possible calling interfaces ⛓

sampler = pm.sampling.Paradram();
Warning
When using the ParaMonte MATLAB library functionalities, particularly ParaMonte samplers in parallel, it would be best to close any such aggressive software/applications as Dropbox, ZoneAlarm, ... that interfere with your ParaMonte MATLAB library output files, potentially causing the tasks to fail and crash before successful completion.
These situations scarcely happen.
Note
On Windows systems, when restarting an old interrupted ParaDRAM simulation, ensure your MATLAB session is also restarted before the simulation restart.
This may be needed as Windows frequently locks access to some or all simulation output files.
To unset an already-set input simulation specification, simply set the simulation attribute to empty double [] or re-instantiate an object of class pm.sampling.Paradram.run().
See also
ParaDRAM simulation specifications listing
ParaDRAM simulation restart functionality
ParaDRAM simulation output files

ParaDRAM Simulation Specifications

The ParaDRAM simulation specifications have lengthy comprehensive descriptions that appear in full in the output report files of every ParaDRAM simulation.

The best way to learn about individual ParaDRAM simulation attributes is to a run a minimal serial simulation as given in the above.
You can also use the sampler.spec.doc() method:

sampler = pm.sampling.Paradram();
sampler.spec.doc()

Example Usage: Serial

First, ensure the ParaMonte +pm package (i.e., folder) is available in your MATLAB paths.

Here is a MATLAB script main.m for a serial ParaDRAM simulation.
Copy and paste the following code into your MATLAB session:

ndim = 4;
sampler = pm.sampling.Paradram();
sampler.run ( @(x) - sum(x.^2) ... getLogFunc: the natural log of the objective function.
, ndim ... ndim: the number of dimensions of the objective function.
);
samples = sampler.readSample();
sample = samples{1};
tile = pm.vis.TileLine(sample.df);
tile.make("coly", sample.slfc + 1 : sample.slfc + ndim, "colc", "sampleLogFunc");
getLogFunc
function getLogFunc(in point)

The mathematical objective function in the above example is a is a multivariate Normal distribution centered at the origin, whose natural logarithm is returned by the lambda (Anonymous) function defined as a function handle input to the ParaDRAM sampler.

Running this code will generate a set of simulation output files (in the current working directory of MATLAB).
Among these, the file suffixed with "_report.txt" contains the full description of all input specifications of the ParaDRAM simulation as well as other information about the simulation results.

Example Usage: Thread-Parallel

First, ensure the ParaMonte +pm package (i.e., folder) is available in your MATLAB paths.

Threading parallelism is possible as of ParaMonte MATLAB version 3.0.0.
However, only singleChain ParaDRAM simulations are supported.

Here is a MATLAB script main.m for a thread-parallel ParaDRAM simulation.
Copy and paste the following code and paste into your MATLAB session:

sampler = pm.sampling.Paradram();
sampler.spec.parallelismNumThread = 0; % use all available threads.
sampler.run ( @(x) - sum(x.^2) ... getLogFunc: the natural log of the objective function.
, 4 ... ndim: the number of dimensions of the objective function.
);
samples = sampler.readSample();
sample = samples{1};
sample.vis.tile.line.make();
sample.vis.triplex.lshc2.make(); % Make a corner scatter/density-contour plot.

The statement sample.vis.tile.line.make(); in the above is equivalent to the following set of lines:

tile = pm.vis.TileLine(sample.df);
tile.make("coly", sample.slfc + 1 : sample.slfc + 4, "colc", "sampleLogFunc");

The mathematical objective function in the above example is a is a multivariate Normal distribution centered at the origin, whose natural logarithm is returned by the lambda (Anonymous) function defined as a function handle input to the ParaDRAM sampler.

Running this code will generate a set of simulation output files (in the current working directory of MATLAB).
Among these, the file suffixed with "_report.txt" contains the full description of all input specifications of the ParaDRAM simulation as well as other information about the simulation results.

Specifying 0 as the number of threads will lead to using all available CPU threads for thread-parallel ParaDRAM simulation.

Note
Benefits of thread-parallelism
Thread-parallel simulations offer a much more flexible and easier approach to benefiting from parallelism without going through the hassle of MPI-parallel simulations.
But they can still potentially offer much faster speed than serial simulations.
The actual speedup depends on a lot of factors.
Moreover, the number of threads is limited to maximum number of physical cores available on your system.
As such, thread-parallel simulations are not scalable.
If you need scalability, checkout MPI-parallelism below.

Example Usage: MPI-Parallel

First, ensure the ParaMonte +pm package (i.e., folder) is available in your MATLAB paths.

MPI-parallel simulations can be slightly more cumbersome than thread-parallel simulations described above because MPI-parallel simulations cannot be performed from within a MATLAB GUI session and require launching MATLAB via a compatible mpiexec launcher.

  1. Ensure you need and will get a speedup by running the an MPI-parallel simulation.
    Typically, your simulation may then benefit from parallelism only if a single evaluation of the objective function takes longer than a few milliseconds.

  2. Ensure the required MPI libraries are installed on your system (You can skip this step if you know that you already have a compatible MPI library installed on your system).
    On the MATLAB command line type the following,

    pm.lib.verify();

    This will verify the existence of a valid MPI library on your system and, if missing, will guide you to install the MPI library on your system.

  3. Once the MPI installation is verified, copy and paste the following code into your MATLAB session:

    fid = fopen("main_mpi.m", "w");
    sourceCode = ...
    "sampler = pm.sampling.Paradram();" + newline + ...
    "%sampler.mpiname = ''; % set this to an explicit MPI library name if needed." + newline + ...
    "sampler.run( @(x) - sum(x.^2) ... getLogFunc: the natural log of the objective function." + newline + ...
    " , 4 ... ndim: the number of dimensions of the objective function" + newline + ...
    " );";
    fprintf(fid, "%s\n", sourceCode);
    fclose(fid);

  4. This will generate a main_mpi.m MATLAB script file in the current working directory of your MATLAB session.
    Now, you can execute this MATLAB script file (main_mpi.m) in parallel.
    To do so, you need to call MATLAB on a command-line, out of MATLAB GUI.

    1. On Windows:
      From within command prompt that recognizes both MATLAB and mpiexec, ideally, the Intel dedicated command-prompt that is shipped with Intel MPI library, type the following,

      mpiexec -localonly -n 3 matlab -batch "main_mpi"
      Note
      In the above MPI launcher command for Windows OS, we assumed that you would be using the Intel MPI library, hence, the reason for the extra flag -localonly.
      This flag runs the parallel code only on one node, but in doing so, it avoids the use of Hydra service and its registration.
      If you are not on a Windows cluster, (e.g., you are using your personal device), then we recommend specifying this flag.

    2. On macOS/Linux:
      From within a Bash terminal that recognizes both MATLAB and mpiexec, type the following,

      mpiexec -n 3 matlab -batch "main_mpi"
      Note
      In both cases in the above, the script main_mpi.m will run on 3 processors.
      Feel free to change the number of processors to any number desired.
      But do not request more than the available number of physical cores on your system.
Warning
Do not add postprocessing codes (such as reading and plotting the output samples) in your MPI-parallel code.
There is no point in doing so, since MATLAB will run in -batch mode for parallel simulations, disabling all plotting capabilities.
Moreover, if you read and postprocess the output files in parallel mode, the task will be done by all parallel processes, potentially overwriting external IO activities of each other.
Only perform the sampling as described above in MPI-parallel mode.


Example usage ⛓

1cd(fileparts(mfilename('fullpath'))); % Change working directory to source code directory.
2addpath('../../../../'); % Add the ParaMonte library root directory to the search path.
3
4%%%%
5%%%% Setup the sampler.
6%%%%
7
8sampler = pm.sampling.Paradram();
9sampler.spec.outputStatus = "retry";
10sampler.spec.proposalStart = [-5, 5];
11sampler.spec.outputFileName = "himmelblau";
12sampler.spec.randomSeed = 28457353; % make sampling reproducible.
13%sampler.spec.outputChainSize = 30000; % Use a small chain size for illustration.
14sampler.spec.parallelismNumThread = []; % Set this to a positive number to request that many parallel threads for the sampling.
15sampler.spec.outputRestartFileFormat = "ascii";
16
17%%%% Set ``mpiname`` to your choice of MPI library
18%%%% ("intel", "openmpi", "mpich", ...) for MPI-parallel applications below.
19%%%% This setting is optional for most MPI-parallel simulations because the
20%%%% ParaMonte library will automatically infer the MPI library usage and type.
21%%%% If the sampler has trouble finding the right MPI-library, help the sampler
22%%%% find the invoke right MPI library build of the ParaMonte library by
23%%%% explicitly specifying its name blow.
24
25% sampler.mpiname = ''; % default
26% sampler.mpiname = "openmpi";
27% sampler.mpiname = "intel";
28% sampler.mpiname = "mpich";
29
30%%%% Developer Warning:
31%%%% Enable `silent` mode when generating
32%%%% the ParaMonte MATLAB documentation for a cleaner doc.
33
34sampler.silent = true;
35
36%%%%
37%%%% Run the sampler.
38%%%%
39
40if true % set to ``false`` to only post-process an existing simulation in the current folder.
41 sampler.run ( @(x) pm.stats.dist.himmelblau.getLogUDF(x(1), x(2)) ...
42 , 2 ...
43 );
44end
45
46%%%%
47%%%% Ensure postprocessing is done by only one parallel process if distributed (MPI) parallelism is enabled.
48%%%%
49
50if pm.lib.mpi.runtime.rankp1() == 1
51
52 %%%%
53 %%%% Postprocess the output chain file.
54 %%%%
55
56 chain = sampler.readChain();
57 chain = chain{1};
58
59 %%%%
60 %%%% Make plots of proposal adaptation.
61 %%%%
62
63 p = pm.vis.PlotScatter(chain.df, "coly", "proposalAdaptation");
64 p.make("axes", {"yscale", "log"});
65 p.savefig("Paradram.himmelblau.proposalAdaptation.png", "-m3");
66
67 chain.vis.proposalAdaptation.line.make()
68 chain.vis.proposalAdaptation.line.savefig("Paradram.himmelblau.proposalAdaptation.line.png", "-m3");
69
70 chain.vis.proposalAdaptation.scatter.make()
71 chain.vis.proposalAdaptation.scatter.savefig("Paradram.himmelblau.proposalAdaptation.scatter.png", "-m3");
72
73 %%%%
74 %%%% Make triplet (corner) plots from the chain file.
75 %%%%
76
77 chain.vis.triplex.lshc2.make();
78 chain.vis.triplex.lshc2.savefig("Paradram.himmelblau.triplex.lshc2.png", "-m3");
79
80 chain.vis.triplex.lshc3.make();
81 chain.vis.triplex.lshc3.savefig("Paradram.himmelblau.triplex.lshc3.png", "-m3");
82
83 chain.vis.triplex.lshcf.make();
84 chain.vis.triplex.lshcf.savefig("Paradram.himmelblau.triplex.lshcf.png", "-m3");
85
86 %%%%
87 %%%% The number `chain.slfc` corresponds to the data column with header "sampleLogFunc"`.
88 %%%%
89
90 p = pm.vis.PlotLineScatter(chain.df, "colx", chain.slfc + 1, "coly", chain.slfc + 2);
91 p.make("colc", "sampleLogFunc");
92 p.savefig("Paradram.himmelblau.domain.2d.png", "-m3");
93
94 p = pm.vis.PlotScatter3(chain.df, "colx", chain.slfc + 1, "coly", chain.slfc + 2, "colz", chain.slfc, "colc", chain.slfc);
95 p.make();
96 p.savefig("Paradram.himmelblau.domain.3d.png", "-m3");
97
98 p = pm.vis.TileLine(chain.df, "tileshape", [2, 1]);
99 p.make("coly", chain.slfc + [1 : 2], "colc", "sampleLogFunc");
100 p.savefig("Paradram.himmelblau.traceplot.png", "-m3");
101
102 %%%%
103 %%%% Postprocess the output restart file.
104 %%%%
105
106 restart = sampler.readRestart();
107 restart = restart{1};
108
109 p = pm.vis.PlotEllipse3(restart.proposalCov, restart.proposalMean, transpose(restart.uniqueStateVisitCount));
110 p.make("axes", {"zscale", "log"});
111 p.savefig("Paradram.himmelblau.proposalCov.png", "-m3");
112
113 %%%%
114 %%%% Postprocess the output report file.
115 %%%%
116
117 report = sampler.readReport();
118 report = report{1};
119
120 for parcond = ["sameeff", "zeroeff"]
121 report.stats.parallelism.speedup.scaling.strong.(parcond).vis.lineScatter.make();
122 report.stats.parallelism.speedup.scaling.strong.(parcond).vis.lineScatter.savefig("Paradram.himmelblau.parallelism.speedup.scaling.strong." + parcond + ".png", "-m3");
123 %p = pm.vis.PlotLineScatter(report.stats.parallelism.speedup.scaling.strong.(parcond).df, "colx", "1", "coly", "2", "colc", "2");
124 %p.make("axes", {"xscale", "log"}, "plot", {"linewidth", 2}, "scatter", {"size", 7});
125 %p.savefig("Paradram.himmelblau.parallelism.speedup.scaling.strong." + parcond + ".png", "-m3");
126 end
127
128end
name
function name(in vendor)
Return the MPI library name as used in naming the ParaMonte MATLAB shared library directories.
find
function find(in vendor)
Return a list of scalar MATLAB strings containing the paths to all detected mpiexec binaries installe...
parallel
function parallel()
Return a scalar MATLAB logical that is true if and only if the current installation of MATLAB contain...
root
function root()
Return a scalar MATLAB string containing the root directory of the ParaMonte library package.

Example output ⛓
1 ParaDRAM - NOTE: Setting up the MATLAB programming language environment for a ParaDRAM simulation...
2 ParaDRAM - NOTE:
3 ParaDRAM - NOTE: The user-specified internal input file for ParaDRAM specifications detected.
4 ParaDRAM - NOTE: All ParaDRAM simulation specifications will be read from the specified internal namelist file...
5
6 ParaDRAM - NOTE: Variable `outputFileName` detected among the user-supplied specifications of the ParaDRAM sampler:
7 ParaDRAM - NOTE: "himmelblau"
8 ParaDRAM - NOTE:
9 ParaDRAM - NOTE: Path to the current working directory:
10 ParaDRAM - NOTE: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/himmelblau"
11 ParaDRAM - NOTE:
12 ParaDRAM - NOTE: Generating the requested directory for the ParaDRAM simulation output files:
13 ParaDRAM - NOTE: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/himmelblau"
14 ParaDRAM - NOTE:
15 ParaDRAM - NOTE: 1 count of preexisting complete simulation runs with the same name prefix were detected.
16 ParaDRAM - NOTE:
17 ParaDRAM - NOTE: The last complete simulation run #1 will be overwritten as requested.
18 ParaDRAM - NOTE: Starting a fresh simulation run #1...
19 ParaDRAM - NOTE:
20 ParaDRAM - NOTE: Running the simulation in serial on 1 process...
21 ParaDRAM - NOTE:
22 ParaDRAM - NOTE: Generating the new output report file:
23 ParaDRAM - NOTE:
24 ParaDRAM - NOTE: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/himmelblau/himmelblau_run1_pid1_report.txt"
25 ParaDRAM - NOTE:
26 ParaDRAM - NOTE: Please see the output *_pid1_report.txt and *_pid1_progress.txt files for further realtime simulation details...
27
28 Accepted/Total Func. Call Dynamic/Overall Acc. Rate Elapsed/Remained Time [s]
29 ========================= ========================= =========================
30
31 356 / 1000 0.3560 / 0.3560 0.0107 / 2.9946
32 635 / 2000 0.2790 / 0.3175 0.0178 / 2.7805
33 899 / 3000 0.2640 / 0.2997 0.0230 / 2.5349
34 1167 / 4000 0.2680 / 0.2918 0.0282 / 2.3905
35 1469 / 5000 0.3020 / 0.2938 0.0333 / 2.2355
36 1796 / 6000 0.3270 / 0.2993 0.0381 / 2.0850
37 2060 / 7000 0.2640 / 0.2943 0.0432 / 2.0556
38 2308 / 8000 0.2480 / 0.2885 0.0478 / 2.0251
39 2586 / 9000 0.2780 / 0.2873 0.0526 / 1.9813
40 2859 / 10000 0.2730 / 0.2859 0.0576 / 1.9570
41 3051 / 11000 0.1920 / 0.2774 0.0621 / 1.9739
42 3338 / 12000 0.2870 / 0.2782 0.0668 / 1.9351
43 3654 / 13000 0.3160 / 0.2811 0.0721 / 1.9000
44 3900 / 14000 0.2460 / 0.2786 0.0766 / 1.8867
45 4157 / 15000 0.2570 / 0.2771 0.0812 / 1.8717
46 4422 / 16000 0.2650 / 0.2764 0.0863 / 1.8644
47 4608 / 17000 0.1860 / 0.2711 0.0910 / 1.8841
48 4859 / 18000 0.2510 / 0.2699 0.0958 / 1.8753
49 5118 / 19000 0.2590 / 0.2694 0.1005 / 1.8636
50 5395 / 20000 0.2770 / 0.2697 0.1056 / 1.8512
51 5621 / 21000 0.2260 / 0.2677 0.1103 / 1.8513
52 5826 / 22000 0.2050 / 0.2648 0.1148 / 1.8562
53 6104 / 23000 0.2780 / 0.2654 0.1199 / 1.8451
54 6346 / 24000 0.2420 / 0.2644 0.1247 / 1.8406
55 6600 / 25000 0.2540 / 0.2640 0.1297 / 1.8360
56 6799 / 26000 0.1990 / 0.2615 0.1350 / 1.8509
57 7059 / 27000 0.2600 / 0.2614 0.1398 / 1.8413
58 7346 / 28000 0.2870 / 0.2624 0.1447 / 1.8255
59 7571 / 29000 0.2250 / 0.2611 0.1494 / 1.8237
60 7869 / 30000 0.2980 / 0.2623 0.1575 / 1.8437
61 8168 / 31000 0.2990 / 0.2635 0.1629 / 1.8312
62 8421 / 32000 0.2530 / 0.2632 0.1685 / 1.8322
63 8751 / 33000 0.3300 / 0.2652 0.1733 / 1.8068
64 8970 / 34000 0.2190 / 0.2638 0.1778 / 1.8040
65 9225 / 35000 0.2550 / 0.2636 0.1826 / 1.7965
66 9403 / 36000 0.1780 / 0.2612 0.1872 / 1.8041
67 9604 / 37000 0.2010 / 0.2596 0.1924 / 1.8106
68 9799 / 38000 0.1950 / 0.2579 0.1987 / 1.8287
69 9993 / 39000 0.1940 / 0.2562 0.2039 / 1.8364
70 10186 / 40000 0.1930 / 0.2546 0.2089 / 1.8417
71 10454 / 41000 0.2680 / 0.2550 0.2143 / 1.8356
72 10701 / 42000 0.2470 / 0.2548 0.2191 / 1.8281
73 10965 / 43000 0.2640 / 0.2550 0.2238 / 1.8170
74 11197 / 44000 0.2320 / 0.2545 0.2289 / 1.8153
75 11390 / 45000 0.1930 / 0.2531 0.2337 / 1.8177
76 11642 / 46000 0.2520 / 0.2531 0.2385 / 1.8103
77 11838 / 47000 0.1960 / 0.2519 0.2433 / 1.8118
78 12067 / 48000 0.2290 / 0.2514 0.2484 / 1.8101
79 12340 / 49000 0.2730 / 0.2518 0.2536 / 1.8012
80 12582 / 50000 0.2420 / 0.2516 0.2600 / 1.8064
81 12855 / 51000 0.2730 / 0.2521 0.2680 / 1.8170
82 13126 / 52000 0.2710 / 0.2524 0.2731 / 1.8075
83 13245 / 53000 0.1190 / 0.2499 0.2779 / 1.8204
84 13426 / 54000 0.1810 / 0.2486 0.2832 / 1.8261
85 13655 / 55000 0.2290 / 0.2483 0.2881 / 1.8218
86 13888 / 56000 0.2330 / 0.2480 0.2936 / 1.8204
87 14100 / 57000 0.2120 / 0.2474 0.2987 / 1.8196
88 14340 / 58000 0.2400 / 0.2472 0.3039 / 1.8151
89 14515 / 59000 0.1750 / 0.2460 0.3089 / 1.8191
90 14686 / 60000 0.1710 / 0.2448 0.3136 / 1.8217
91 15024 / 61000 0.3380 / 0.2463 0.3189 / 1.8037
92 15313 / 62000 0.2890 / 0.2470 0.3244 / 1.7939
93 15602 / 63000 0.2890 / 0.2477 0.3293 / 1.7812
94 15849 / 64000 0.2470 / 0.2476 0.3342 / 1.7743
95 16136 / 65000 0.2870 / 0.2482 0.3391 / 1.7623
96 16405 / 66000 0.2690 / 0.2486 0.3447 / 1.7565
97 16644 / 67000 0.2390 / 0.2484 0.3495 / 1.7504
98 16862 / 68000 0.2180 / 0.2480 0.3543 / 1.7470
99 17155 / 69000 0.2930 / 0.2486 0.3595 / 1.7359
100 17387 / 70000 0.2320 / 0.2484 0.3643 / 1.7310
101 17657 / 71000 0.2700 / 0.2487 0.3692 / 1.7216
102 17935 / 72000 0.2780 / 0.2491 0.3746 / 1.7139
103 18230 / 73000 0.2950 / 0.2497 0.3802 / 1.7053
104 18508 / 74000 0.2780 / 0.2501 0.3862 / 1.7005
105 18703 / 75000 0.1950 / 0.2494 0.3920 / 1.7038
106 18977 / 76000 0.2740 / 0.2497 0.4002 / 1.7086
107 19277 / 77000 0.3000 / 0.2504 0.4055 / 1.6982
108 19533 / 78000 0.2560 / 0.2504 0.4104 / 1.6907
109 19640 / 79000 0.1070 / 0.2486 0.4150 / 1.6980
110 19874 / 80000 0.2340 / 0.2484 0.4204 / 1.6948
111 20150 / 81000 0.2760 / 0.2488 0.4255 / 1.6860
112 20417 / 82000 0.2670 / 0.2490 0.4305 / 1.6778
113 20670 / 83000 0.2530 / 0.2490 0.4357 / 1.6722
114 20976 / 84000 0.3060 / 0.2497 0.4407 / 1.6604
115 21213 / 85000 0.2370 / 0.2496 0.4457 / 1.6555
116 21553 / 86000 0.3400 / 0.2506 0.4537 / 1.6515
117 21785 / 87000 0.2320 / 0.2504 0.4586 / 1.6465
118 22023 / 88000 0.2380 / 0.2503 0.4633 / 1.6405
119 22326 / 89000 0.3030 / 0.2509 0.4695 / 1.6333
120 22507 / 90000 0.1810 / 0.2501 0.4745 / 1.6337
121 22769 / 91000 0.2620 / 0.2502 0.4797 / 1.6270
122 22951 / 92000 0.1820 / 0.2495 0.4849 / 1.6278
123 23283 / 93000 0.3320 / 0.2504 0.4899 / 1.6143
124 23582 / 94000 0.2990 / 0.2509 0.4948 / 1.6036
125 23763 / 95000 0.1810 / 0.2501 0.4998 / 1.6034
126 24022 / 96000 0.2590 / 0.2502 0.5047 / 1.5962
127 24271 / 97000 0.2490 / 0.2502 0.5098 / 1.5907
128 24485 / 98000 0.2140 / 0.2498 0.5148 / 1.5878
129 24679 / 99000 0.1940 / 0.2493 0.5203 / 1.5878
130 24989 / 100000 0.3100 / 0.2499 0.5264 / 1.5802
131 25203 / 101000 0.2140 / 0.2495 0.5320 / 1.5789
132 25435 / 102000 0.2320 / 0.2494 0.5375 / 1.5757
133 25665 / 103000 0.2300 / 0.2492 0.5424 / 1.5709
134 25880 / 104000 0.2150 / 0.2488 0.5473 / 1.5674
135 26120 / 105000 0.2400 / 0.2488 0.5522 / 1.5619
136 26397 / 106000 0.2770 / 0.2490 0.5570 / 1.5532
137 26720 / 107000 0.3230 / 0.2497 0.5620 / 1.5413
138 27034 / 108000 0.3140 / 0.2503 0.5689 / 1.5355
139 27269 / 109000 0.2350 / 0.2502 0.5753 / 1.5345
140 27541 / 110000 0.2720 / 0.2504 0.5810 / 1.5287
141 27819 / 111000 0.2780 / 0.2506 0.5865 / 1.5219
142 28077 / 112000 0.2580 / 0.2507 0.5915 / 1.5152
143 28297 / 113000 0.2200 / 0.2504 0.5967 / 1.5121
144 28539 / 114000 0.2420 / 0.2503 0.6017 / 1.5066
145 28800 / 115000 0.2610 / 0.2504 0.6065 / 1.4995
146 29039 / 116000 0.2390 / 0.2503 0.6116 / 1.4945
147 29196 / 117000 0.1570 / 0.2495 0.6163 / 1.4947
148 29427 / 118000 0.2310 / 0.2494 0.6211 / 1.4896
149 29683 / 119000 0.2560 / 0.2494 0.6262 / 1.4834
150 29993 / 120000 0.3100 / 0.2499 0.6324 / 1.4760
151 30213 / 121000 0.2200 / 0.2497 0.6373 / 1.4720
152 30524 / 122000 0.3110 / 0.2502 0.6425 / 1.4623
153 30825 / 123000 0.3010 / 0.2506 0.6497 / 1.4581
154 30960 / 124000 0.1350 / 0.2497 0.6543 / 1.4590
155 31267 / 125000 0.3070 / 0.2501 0.6596 / 1.4499
156 31570 / 126000 0.3030 / 0.2506 0.6646 / 1.4405
157 31818 / 127000 0.2480 / 0.2505 0.6694 / 1.4345
158 32066 / 128000 0.2480 / 0.2505 0.6743 / 1.4285
159 32393 / 129000 0.3270 / 0.2511 0.6793 / 1.4177
160 32604 / 130000 0.2110 / 0.2508 0.6843 / 1.4144
161 32809 / 131000 0.2050 / 0.2505 0.6891 / 1.4113
162 33021 / 132000 0.2120 / 0.2502 0.6941 / 1.4079
163 33332 / 133000 0.3110 / 0.2506 0.6992 / 1.3985
164 33511 / 134000 0.1790 / 0.2501 0.7038 / 1.3965
165 33802 / 135000 0.2910 / 0.2504 0.7095 / 1.3895
166 34088 / 136000 0.2860 / 0.2506 0.7154 / 1.3833
167 34336 / 137000 0.2480 / 0.2506 0.7201 / 1.3772
168 34618 / 138000 0.2820 / 0.2509 0.7258 / 1.3709
169 34876 / 139000 0.2580 / 0.2509 0.7306 / 1.3642
170 35163 / 140000 0.2870 / 0.2512 0.7356 / 1.3564
171 35389 / 141000 0.2260 / 0.2510 0.7409 / 1.3528
172 35604 / 142000 0.2150 / 0.2507 0.7457 / 1.3488
173 35829 / 143000 0.2250 / 0.2506 0.7505 / 1.3441
174 36056 / 144000 0.2270 / 0.2504 0.7563 / 1.3413
175 36295 / 145000 0.2390 / 0.2503 0.7632 / 1.3395
176 36536 / 146000 0.2410 / 0.2502 0.7693 / 1.3362
177 36779 / 147000 0.2430 / 0.2502 0.7749 / 1.3319
178 37064 / 148000 0.2850 / 0.2504 0.7799 / 1.3243
179 37320 / 149000 0.2560 / 0.2505 0.7850 / 1.3184
180 37614 / 150000 0.2940 / 0.2508 0.7905 / 1.3111
181 37884 / 151000 0.2700 / 0.2509 0.7955 / 1.3043
182 38082 / 152000 0.1980 / 0.2505 0.8006 / 1.3017
183 38302 / 153000 0.2200 / 0.2503 0.8061 / 1.2984
184 38552 / 154000 0.2500 / 0.2503 0.8110 / 1.2926
185 38815 / 155000 0.2630 / 0.2504 0.8197 / 1.2921
186 39030 / 156000 0.2150 / 0.2502 0.8260 / 1.2904
187 39266 / 157000 0.2360 / 0.2501 0.8337 / 1.2895
188 39504 / 158000 0.2380 / 0.2500 0.8388 / 1.2845
189 39804 / 159000 0.3000 / 0.2503 0.8437 / 1.2759
190 40080 / 160000 0.2760 / 0.2505 0.8501 / 1.2709
191 40325 / 161000 0.2450 / 0.2505 0.8552 / 1.2655
192 40580 / 162000 0.2550 / 0.2505 0.8600 / 1.2593
193 40815 / 163000 0.2350 / 0.2504 0.8663 / 1.2562
194 41088 / 164000 0.2730 / 0.2505 0.8715 / 1.2495
195 41307 / 165000 0.2190 / 0.2503 0.8763 / 1.2451
196 41567 / 166000 0.2600 / 0.2504 0.8814 / 1.2390
197 41877 / 167000 0.3100 / 0.2508 0.8866 / 1.2305
198 42097 / 168000 0.2200 / 0.2506 0.8916 / 1.2264
199 42336 / 169000 0.2390 / 0.2505 0.8966 / 1.2212
200 42597 / 170000 0.2610 / 0.2506 0.9026 / 1.2163
201 42823 / 171000 0.2260 / 0.2504 0.9099 / 1.2148
202 43088 / 172000 0.2650 / 0.2505 0.9154 / 1.2091
203 43337 / 173000 0.2490 / 0.2505 0.9203 / 1.2033
204 43600 / 174000 0.2630 / 0.2506 0.9253 / 1.1969
205 43877 / 175000 0.2770 / 0.2507 0.9307 / 1.1904
206 44222 / 176000 0.3450 / 0.2513 0.9357 / 1.1802
207 44474 / 177000 0.2520 / 0.2513 0.9405 / 1.1742
208 44749 / 178000 0.2750 / 0.2514 0.9463 / 1.1684
209 45003 / 179000 0.2540 / 0.2514 0.9512 / 1.1624
210 45288 / 180000 0.2850 / 0.2516 0.9577 / 1.1570
211 45573 / 181000 0.2850 / 0.2518 0.9646 / 1.1520
212 45800 / 182000 0.2270 / 0.2516 0.9698 / 1.1476
213 46022 / 183000 0.2220 / 0.2515 0.9752 / 1.1437
214 46281 / 184000 0.2590 / 0.2515 0.9816 / 1.1393
215 46527 / 185000 0.2460 / 0.2515 0.9866 / 1.1339
216 46827 / 186000 0.3000 / 0.2518 0.9916 / 1.1260
217 47101 / 187000 0.2740 / 0.2519 0.9969 / 1.1196
218 47353 / 188000 0.2520 / 0.2519 1.0016 / 1.1136
219 47594 / 189000 0.2410 / 0.2518 1.0062 / 1.1080
220 47798 / 190000 0.2040 / 0.2516 1.0108 / 1.1040
221 48016 / 191000 0.2180 / 0.2514 1.0158 / 1.0997
222 48251 / 192000 0.2350 / 0.2513 1.0206 / 1.0946
223 48490 / 193000 0.2390 / 0.2512 1.0253 / 1.0891
224 48784 / 194000 0.2940 / 0.2515 1.0304 / 1.0818
225 49047 / 195000 0.2630 / 0.2515 1.0354 / 1.0756
226 49291 / 196000 0.2440 / 0.2515 1.0401 / 1.0700
227 49570 / 197000 0.2790 / 0.2516 1.0453 / 1.0634
228 49727 / 198000 0.1570 / 0.2511 1.0500 / 1.0615
229 50000 / 199000 0.2730 / 0.2513 1.0548 / 1.0548
230 50189 / 200000 0.1890 / 0.2509 1.0596 / 1.0516
231 50391 / 201000 0.2020 / 0.2507 1.0641 / 1.0476
232 50612 / 202000 0.2210 / 0.2506 1.0688 / 1.0430
233 50873 / 203000 0.2610 / 0.2506 1.0735 / 1.0367
234 51131 / 204000 0.2580 / 0.2506 1.0792 / 1.0315
235 51500 / 205000 0.3690 / 0.2512 1.0859 / 1.0226
236 51778 / 206000 0.2780 / 0.2513 1.0906 / 1.0157
237 52007 / 207000 0.2290 / 0.2512 1.0961 / 1.0115
238 52358 / 208000 0.3510 / 0.2517 1.1034 / 1.0040
239 52676 / 209000 0.3180 / 0.2520 1.1088 / 0.9962
240 52923 / 210000 0.2470 / 0.2520 1.1139 / 0.9908
241 53100 / 211000 0.1770 / 0.2517 1.1184 / 0.9878
242 53294 / 212000 0.1940 / 0.2514 1.1231 / 0.9842
243 53569 / 213000 0.2750 / 0.2515 1.1278 / 0.9775
244 53778 / 214000 0.2090 / 0.2513 1.1327 / 0.9736
245 53994 / 215000 0.2160 / 0.2511 1.1373 / 0.9691
246 54251 / 216000 0.2570 / 0.2512 1.1421 / 0.9632
247 54470 / 217000 0.2190 / 0.2510 1.1474 / 0.9591
248 54667 / 218000 0.1970 / 0.2508 1.1524 / 0.9556
249 54938 / 219000 0.2710 / 0.2509 1.1580 / 0.9499
250 55126 / 220000 0.1880 / 0.2506 1.1641 / 0.9476
251 55390 / 221000 0.2640 / 0.2506 1.1702 / 0.9424
252 55642 / 222000 0.2520 / 0.2506 1.1756 / 0.9372
253 55930 / 223000 0.2880 / 0.2508 1.1807 / 0.9304
254 56148 / 224000 0.2180 / 0.2507 1.1855 / 0.9259
255 56322 / 225000 0.1740 / 0.2503 1.1901 / 0.9229
256 56611 / 226000 0.2890 / 0.2505 1.1956 / 0.9164
257 56925 / 227000 0.3140 / 0.2508 1.2008 / 0.9087
258 57148 / 228000 0.2230 / 0.2506 1.2059 / 0.9042
259 57413 / 229000 0.2650 / 0.2507 1.2110 / 0.8983
260 57623 / 230000 0.2100 / 0.2505 1.2162 / 0.8944
261 57871 / 231000 0.2480 / 0.2505 1.2210 / 0.8889
262 58118 / 232000 0.2470 / 0.2505 1.2260 / 0.8835
263 58444 / 233000 0.3260 / 0.2508 1.2309 / 0.8752
264 58673 / 234000 0.2290 / 0.2507 1.2359 / 0.8705
265 58946 / 235000 0.2730 / 0.2508 1.2414 / 0.8646
266 59136 / 236000 0.1900 / 0.2506 1.2460 / 0.8610
267 59408 / 237000 0.2720 / 0.2507 1.2508 / 0.8547
268 59631 / 238000 0.2230 / 0.2506 1.2561 / 0.8504
269 59917 / 239000 0.2860 / 0.2507 1.2610 / 0.8436
270 60192 / 240000 0.2750 / 0.2508 1.2661 / 0.8373
271 60465 / 241000 0.2730 / 0.2509 1.2717 / 0.8315
272 60778 / 242000 0.3130 / 0.2511 1.2769 / 0.8240
273 61071 / 243000 0.2930 / 0.2513 1.2823 / 0.8174
274 61365 / 244000 0.2940 / 0.2515 1.2876 / 0.8107
275 61524 / 245000 0.1590 / 0.2511 1.2928 / 0.8085
276 61811 / 246000 0.2870 / 0.2513 1.2976 / 0.8017
277 62094 / 247000 0.2830 / 0.2514 1.3025 / 0.7951
278 62329 / 248000 0.2350 / 0.2513 1.3074 / 0.7902
279 62518 / 249000 0.1890 / 0.2511 1.3121 / 0.7867
280 62763 / 250000 0.2450 / 0.2511 1.3171 / 0.7814
281 63014 / 251000 0.2510 / 0.2511 1.3221 / 0.7760
282 63185 / 252000 0.1710 / 0.2507 1.3268 / 0.7731
283 63436 / 253000 0.2510 / 0.2507 1.3330 / 0.7684
284 63706 / 254000 0.2700 / 0.2508 1.3380 / 0.7623
285 63862 / 255000 0.1560 / 0.2504 1.3427 / 0.7598
286 64162 / 256000 0.3000 / 0.2506 1.3475 / 0.7526
287 64542 / 257000 0.3800 / 0.2511 1.3534 / 0.7435
288 64857 / 258000 0.3150 / 0.2514 1.3583 / 0.7360
289 65075 / 259000 0.2180 / 0.2513 1.3629 / 0.7314
290 65382 / 260000 0.3070 / 0.2515 1.3680 / 0.7243
291 65621 / 261000 0.2390 / 0.2514 1.3727 / 0.7191
292 65808 / 262000 0.1870 / 0.2512 1.3773 / 0.7156
293 66007 / 263000 0.1990 / 0.2510 1.3829 / 0.7122
294 66342 / 264000 0.3350 / 0.2513 1.3881 / 0.7042
295 66534 / 265000 0.1920 / 0.2511 1.3934 / 0.7009
296 66814 / 266000 0.2800 / 0.2512 1.3989 / 0.6948
297 67047 / 267000 0.2330 / 0.2511 1.4038 / 0.6900
298 67282 / 268000 0.2350 / 0.2511 1.4086 / 0.6850
299 67613 / 269000 0.3310 / 0.2513 1.4141 / 0.6774
300 67798 / 270000 0.1850 / 0.2511 1.4187 / 0.6738
301 68054 / 271000 0.2560 / 0.2511 1.4233 / 0.6681
302 68215 / 272000 0.1610 / 0.2508 1.4279 / 0.6653
303 68377 / 273000 0.1620 / 0.2505 1.4338 / 0.6631
304 68655 / 274000 0.2780 / 0.2506 1.4385 / 0.6568
305 68873 / 275000 0.2180 / 0.2504 1.4453 / 0.6532
306 69164 / 276000 0.2910 / 0.2506 1.4531 / 0.6478
307 69403 / 277000 0.2390 / 0.2506 1.4579 / 0.6427
308 69588 / 278000 0.1850 / 0.2503 1.4627 / 0.6392
309 69815 / 279000 0.2270 / 0.2502 1.4675 / 0.6345
310 70098 / 280000 0.2830 / 0.2503 1.4724 / 0.6281
311 70264 / 281000 0.1660 / 0.2500 1.4776 / 0.6253
312 70509 / 282000 0.2450 / 0.2500 1.4831 / 0.6203
313 70709 / 283000 0.2000 / 0.2499 1.4877 / 0.6163
314 70971 / 284000 0.2620 / 0.2499 1.4926 / 0.6105
315 71186 / 285000 0.2150 / 0.2498 1.4976 / 0.6062
316 71441 / 286000 0.2550 / 0.2498 1.5033 / 0.6010
317 71643 / 287000 0.2020 / 0.2496 1.5083 / 0.5970
318 71873 / 288000 0.2300 / 0.2496 1.5136 / 0.5923
319 72164 / 289000 0.2910 / 0.2497 1.5188 / 0.5859
320 72506 / 290000 0.3420 / 0.2500 1.5239 / 0.5779
321 72749 / 291000 0.2430 / 0.2500 1.5289 / 0.5727
322 73005 / 292000 0.2560 / 0.2500 1.5340 / 0.5672
323 73244 / 293000 0.2390 / 0.2500 1.5386 / 0.5620
324 73436 / 294000 0.1920 / 0.2498 1.5436 / 0.5584
325 73667 / 295000 0.2310 / 0.2497 1.5483 / 0.5535
326 73860 / 296000 0.1930 / 0.2495 1.5530 / 0.5496
327 74108 / 297000 0.2480 / 0.2495 1.5581 / 0.5444
328 74297 / 298000 0.1890 / 0.2493 1.5628 / 0.5406
329 74581 / 299000 0.2840 / 0.2494 1.5677 / 0.5343
330 74866 / 300000 0.2850 / 0.2496 1.5730 / 0.5281
331 75198 / 301000 0.3320 / 0.2498 1.5784 / 0.5206
332 75489 / 302000 0.2910 / 0.2500 1.5841 / 0.5144
333 75784 / 303000 0.2950 / 0.2501 1.5892 / 0.5078
334 76039 / 304000 0.2550 / 0.2501 1.5940 / 0.5023
335 76337 / 305000 0.2980 / 0.2503 1.5988 / 0.4956
336 76626 / 306000 0.2890 / 0.2504 1.6039 / 0.4892
337 76868 / 307000 0.2420 / 0.2504 1.6091 / 0.4842
338 77156 / 308000 0.2880 / 0.2505 1.6141 / 0.4779
339 77399 / 309000 0.2430 / 0.2505 1.6190 / 0.4728
340 77652 / 310000 0.2530 / 0.2505 1.6240 / 0.4674
341 77849 / 311000 0.1970 / 0.2503 1.6288 / 0.4635
342 78124 / 312000 0.2750 / 0.2504 1.6368 / 0.4583
343 78329 / 313000 0.2050 / 0.2503 1.6425 / 0.4544
344 78594 / 314000 0.2650 / 0.2503 1.6474 / 0.4487
345 78886 / 315000 0.2920 / 0.2504 1.6542 / 0.4427
346 79202 / 316000 0.3160 / 0.2506 1.6591 / 0.4357
347 79419 / 317000 0.2170 / 0.2505 1.6638 / 0.4312
348 79662 / 318000 0.2430 / 0.2505 1.6706 / 0.4265
349 79950 / 319000 0.2880 / 0.2506 1.6759 / 0.4203
350 80151 / 320000 0.2010 / 0.2505 1.6804 / 0.4162
351 80348 / 321000 0.1970 / 0.2503 1.6856 / 0.4123
352 80659 / 322000 0.3110 / 0.2505 1.6906 / 0.4054
353 80934 / 323000 0.2750 / 0.2506 1.6956 / 0.3994
354 81219 / 324000 0.2850 / 0.2507 1.7008 / 0.3933
355 81496 / 325000 0.2770 / 0.2508 1.7067 / 0.3875
356 81713 / 326000 0.2170 / 0.2507 1.7119 / 0.3831
357 82051 / 327000 0.3380 / 0.2509 1.7172 / 0.3756
358 82304 / 328000 0.2530 / 0.2509 1.7219 / 0.3702
359 82533 / 329000 0.2290 / 0.2509 1.7266 / 0.3654
360 82801 / 330000 0.2680 / 0.2509 1.7314 / 0.3596
361 82986 / 331000 0.1850 / 0.2507 1.7365 / 0.3560
362 83252 / 332000 0.2660 / 0.2508 1.7412 / 0.3503
363 83478 / 333000 0.2260 / 0.2507 1.7460 / 0.3456
364 83690 / 334000 0.2120 / 0.2506 1.7514 / 0.3413
365 83855 / 335000 0.1650 / 0.2503 1.7562 / 0.3381
366 84177 / 336000 0.3220 / 0.2505 1.7634 / 0.3315
367 84585 / 337000 0.4080 / 0.2510 1.7710 / 0.3228
368 84866 / 338000 0.2810 / 0.2511 1.7762 / 0.3167
369 85089 / 339000 0.2230 / 0.2510 1.7817 / 0.3122
370 85304 / 340000 0.2150 / 0.2509 1.7866 / 0.3078
371 85510 / 341000 0.2060 / 0.2508 1.7913 / 0.3035
372 85679 / 342000 0.1690 / 0.2505 1.7966 / 0.3003
373 86018 / 343000 0.3390 / 0.2508 1.8023 / 0.2930
374 86259 / 344000 0.2410 / 0.2508 1.8069 / 0.2878
375 86460 / 345000 0.2010 / 0.2506 1.8120 / 0.2838
376 86584 / 346000 0.1240 / 0.2502 1.8197 / 0.2820
377 86880 / 347000 0.2960 / 0.2504 1.8249 / 0.2756
378 87133 / 348000 0.2530 / 0.2504 1.8304 / 0.2703
379 87418 / 349000 0.2850 / 0.2505 1.8353 / 0.2642
380 87646 / 350000 0.2280 / 0.2504 1.8399 / 0.2593
381 87950 / 351000 0.3040 / 0.2506 1.8451 / 0.2528
382 88253 / 352000 0.3030 / 0.2507 1.8503 / 0.2463
383 88535 / 353000 0.2820 / 0.2508 1.8553 / 0.2403
384 88836 / 354000 0.3010 / 0.2509 1.8617 / 0.2340
385 89149 / 355000 0.3130 / 0.2511 1.8670 / 0.2273
386 89356 / 356000 0.2070 / 0.2510 1.8719 / 0.2230
387 89590 / 357000 0.2340 / 0.2510 1.8769 / 0.2181
388 89876 / 358000 0.2860 / 0.2511 1.8817 / 0.2120
389 90163 / 359000 0.2870 / 0.2512 1.8867 / 0.2058
390 90407 / 360000 0.2440 / 0.2511 1.8929 / 0.2008
391 90703 / 361000 0.2960 / 0.2513 1.8991 / 0.1947
392 90949 / 362000 0.2460 / 0.2512 1.9039 / 0.1895
393 91236 / 363000 0.2870 / 0.2513 1.9088 / 0.1834
394 91515 / 364000 0.2790 / 0.2514 1.9134 / 0.1774
395 91738 / 365000 0.2230 / 0.2513 1.9180 / 0.1727
396 91993 / 366000 0.2550 / 0.2513 1.9233 / 0.1674
397 92280 / 367000 0.2870 / 0.2514 1.9280 / 0.1613
398 92533 / 368000 0.2530 / 0.2514 1.9326 / 0.1560
399 92792 / 369000 0.2590 / 0.2515 1.9373 / 0.1505
400 93077 / 370000 0.2850 / 0.2516 1.9425 / 0.1445
401 93286 / 371000 0.2090 / 0.2514 1.9473 / 0.1402
402 93524 / 372000 0.2380 / 0.2514 1.9519 / 0.1352
403 93795 / 373000 0.2710 / 0.2515 1.9614 / 0.1298
404 94045 / 374000 0.2500 / 0.2515 1.9672 / 0.1246
405 94276 / 375000 0.2310 / 0.2514 1.9721 / 0.1197
406 94511 / 376000 0.2350 / 0.2514 1.9773 / 0.1148
407 94815 / 377000 0.3040 / 0.2515 1.9821 / 0.1084
408 95049 / 378000 0.2340 / 0.2515 1.9870 / 0.1035
409 95290 / 379000 0.2410 / 0.2514 1.9919 / 0.0985
410 95574 / 380000 0.2840 / 0.2515 1.9965 / 0.0925
411 95826 / 381000 0.2520 / 0.2515 2.0014 / 0.0872
412 96069 / 382000 0.2430 / 0.2515 2.0059 / 0.0821
413 96280 / 383000 0.2110 / 0.2514 2.0110 / 0.0777
414 96638 / 384000 0.3580 / 0.2517 2.0193 / 0.0703
415 96877 / 385000 0.2390 / 0.2516 2.0241 / 0.0652
416 97117 / 386000 0.2400 / 0.2516 2.0287 / 0.0602
417 97455 / 387000 0.3380 / 0.2518 2.0344 / 0.0531
418 97678 / 388000 0.2230 / 0.2517 2.0389 / 0.0485
419 97920 / 389000 0.2420 / 0.2517 2.0434 / 0.0434
420 98047 / 390000 0.1270 / 0.2514 2.0493 / 0.0408
421 98261 / 391000 0.2140 / 0.2513 2.0538 / 0.0363
422 98484 / 392000 0.2230 / 0.2512 2.0583 / 0.0317
423 98728 / 393000 0.2440 / 0.2512 2.0629 / 0.0266
424 98936 / 394000 0.2080 / 0.2511 2.0687 / 0.0222
425 99032 / 395000 0.0960 / 0.2507 2.0730 / 0.0203
426 99221 / 396000 0.1890 / 0.2506 2.0779 / 0.0163
427 99415 / 397000 0.1940 / 0.2504 2.0826 / 0.0123
428 99662 / 398000 0.2470 / 0.2504 2.0891 / 0.0071
429 99894 / 399000 0.2320 / 0.2504 2.0936 / 0.0022
430 100000 / 399632 0.1060 / 0.2502 2.0964 / 0.0000
431
432
433 ParaDRAM - NOTE: Computing the statistical properties of the Markov chain...
434
435 ParaDRAM - NOTE: Computing the final refined i.i.d. sample size...
436
437 ParaDRAM - NOTE: Generating the output sample file:
438 ParaDRAM - NOTE: /home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/himmelblau/himmelblau_run1_pid1_sample.txt
439
440 ParaDRAM - NOTE: Computing the statistical properties of the final output sample...
441
442
443 ParaDRAM - NOTE: Mission Accomplished.
444
445| 50%
446| 100% done in 0.069041 seconds.
Paradram
This is the ParaDRAM class for generating instances of serial and parallel Delayed-Rejection Adaptive...
Definition: Paradram.m:18
Paradram::run
function run(in self, in getLogFunc, in ndim)
Run the ParaDRAM sampler and return nothing.
home
function home()
Return a MATLAB string containing the absolute path to the system home directory.
lib
function lib()
Return a scalar MATLAB string containing the path to the lib directory of the ParaMonte library packa...

Visualization of the example output ⛓























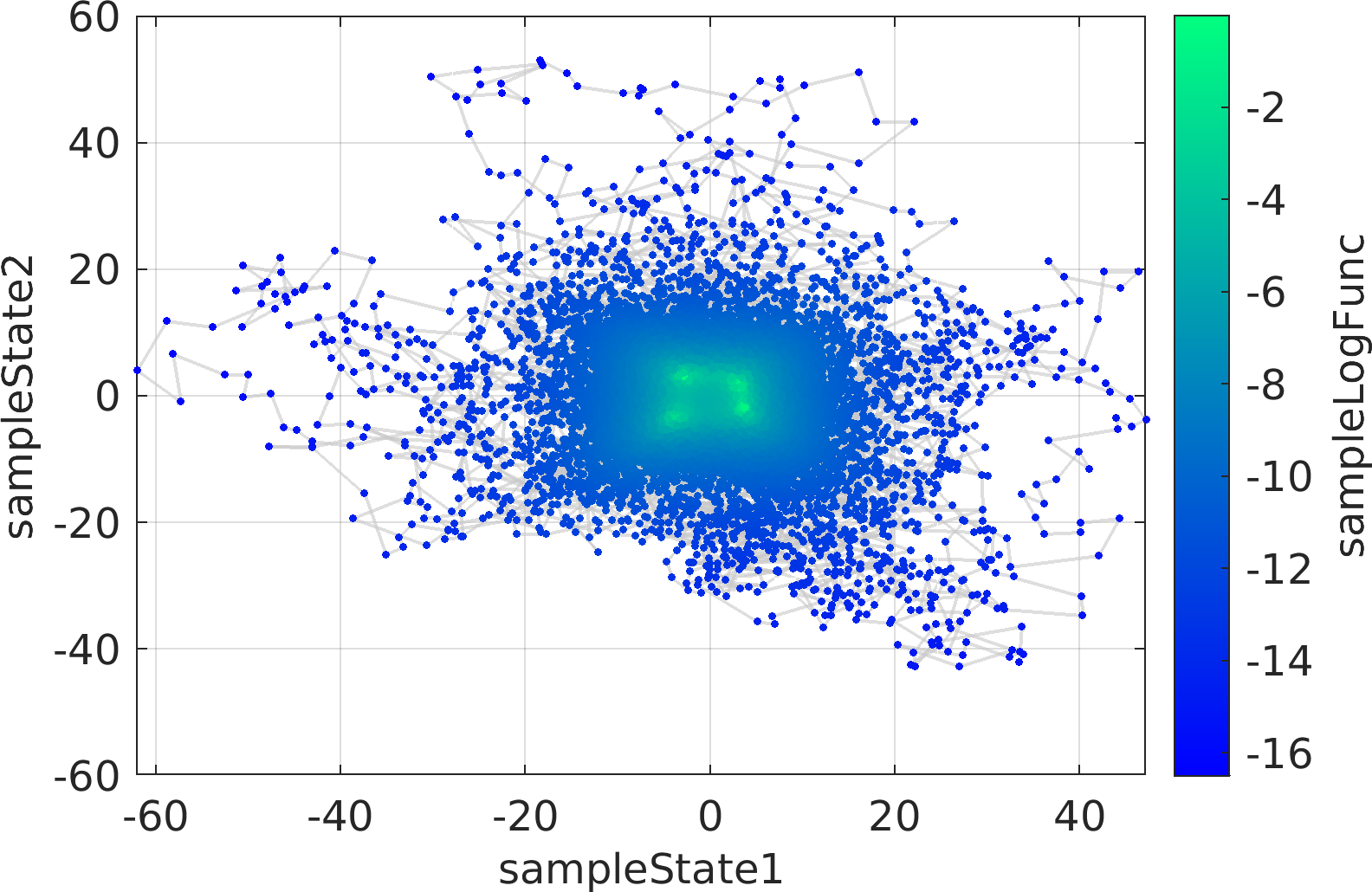
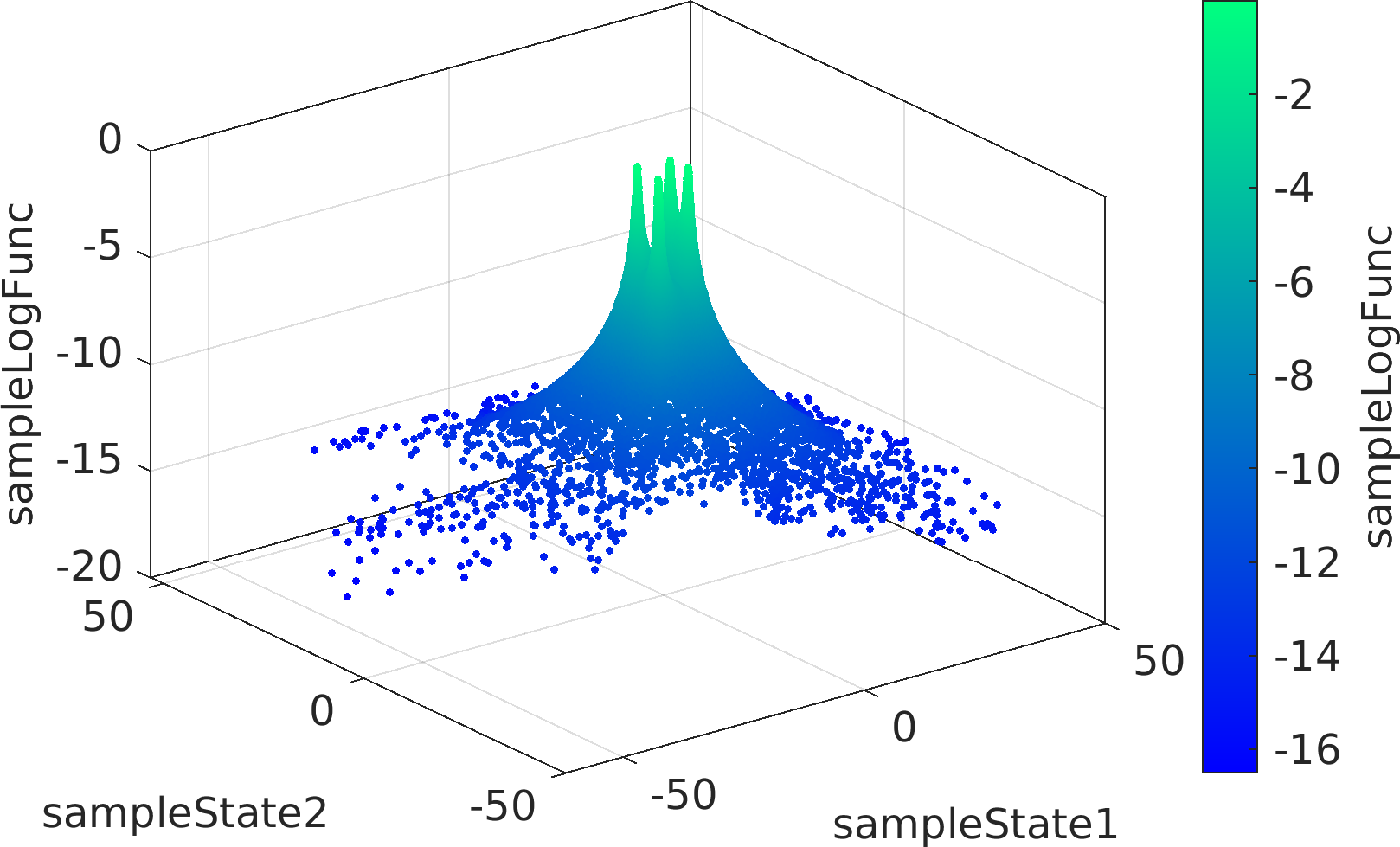
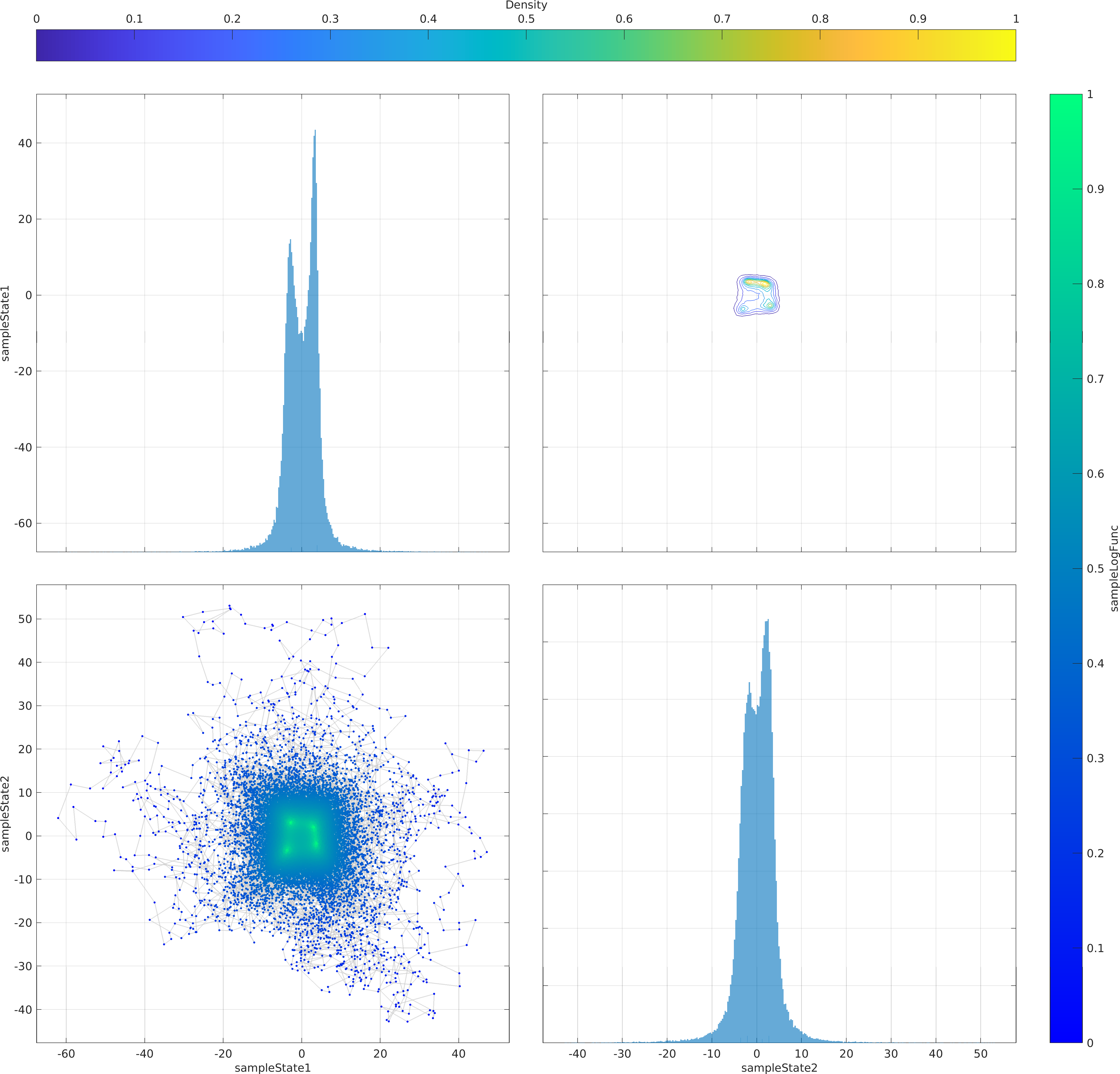
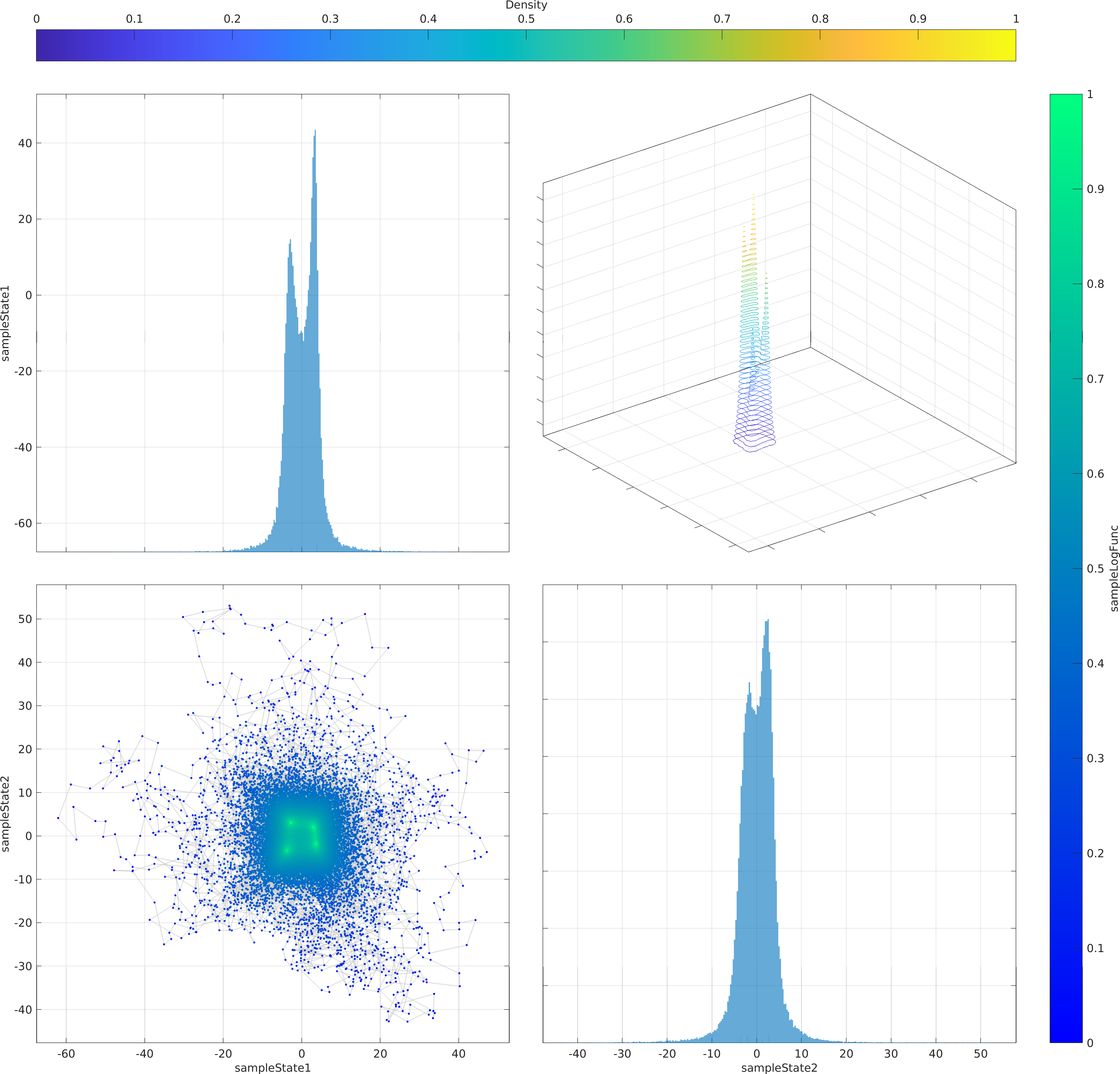
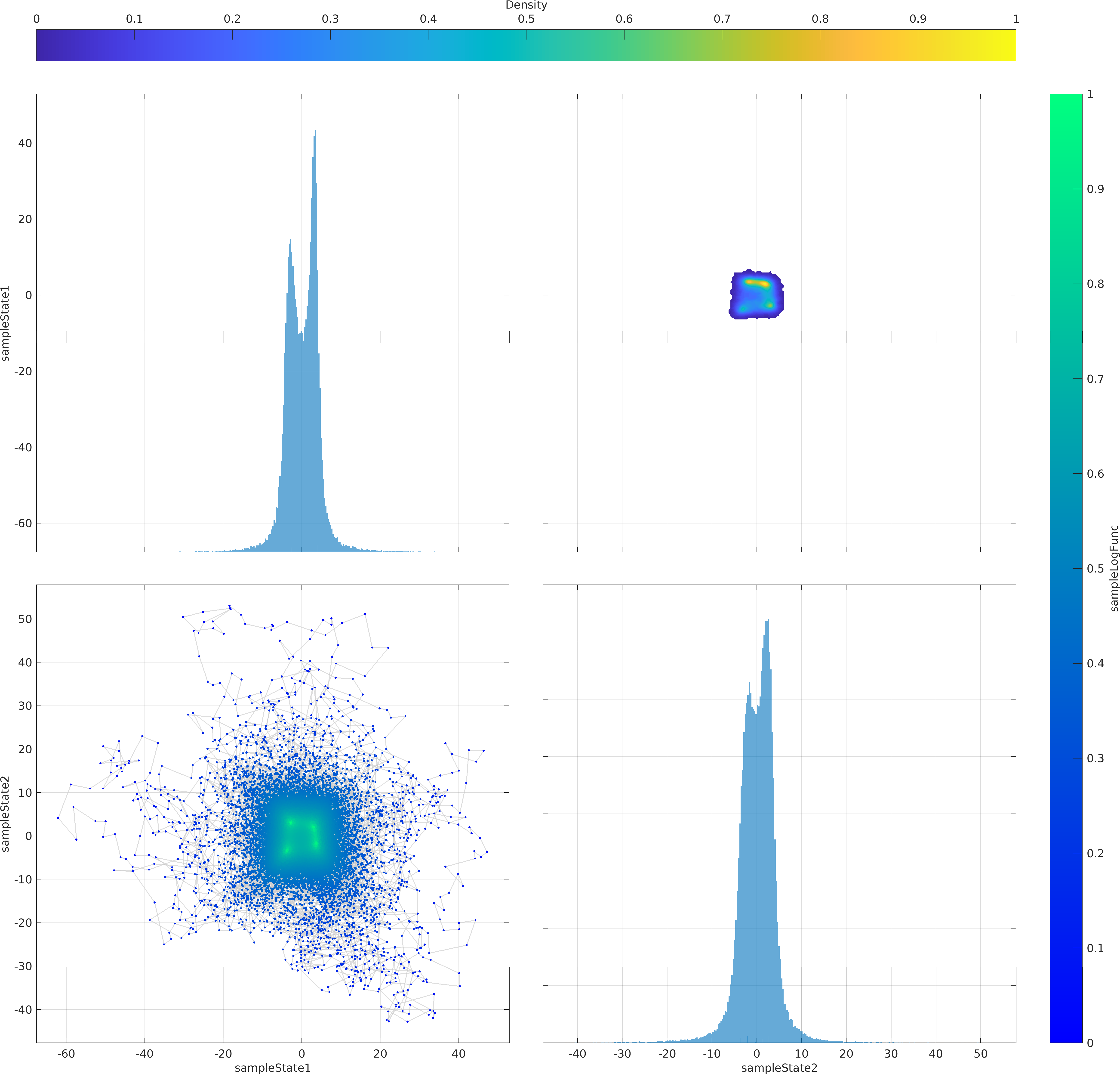
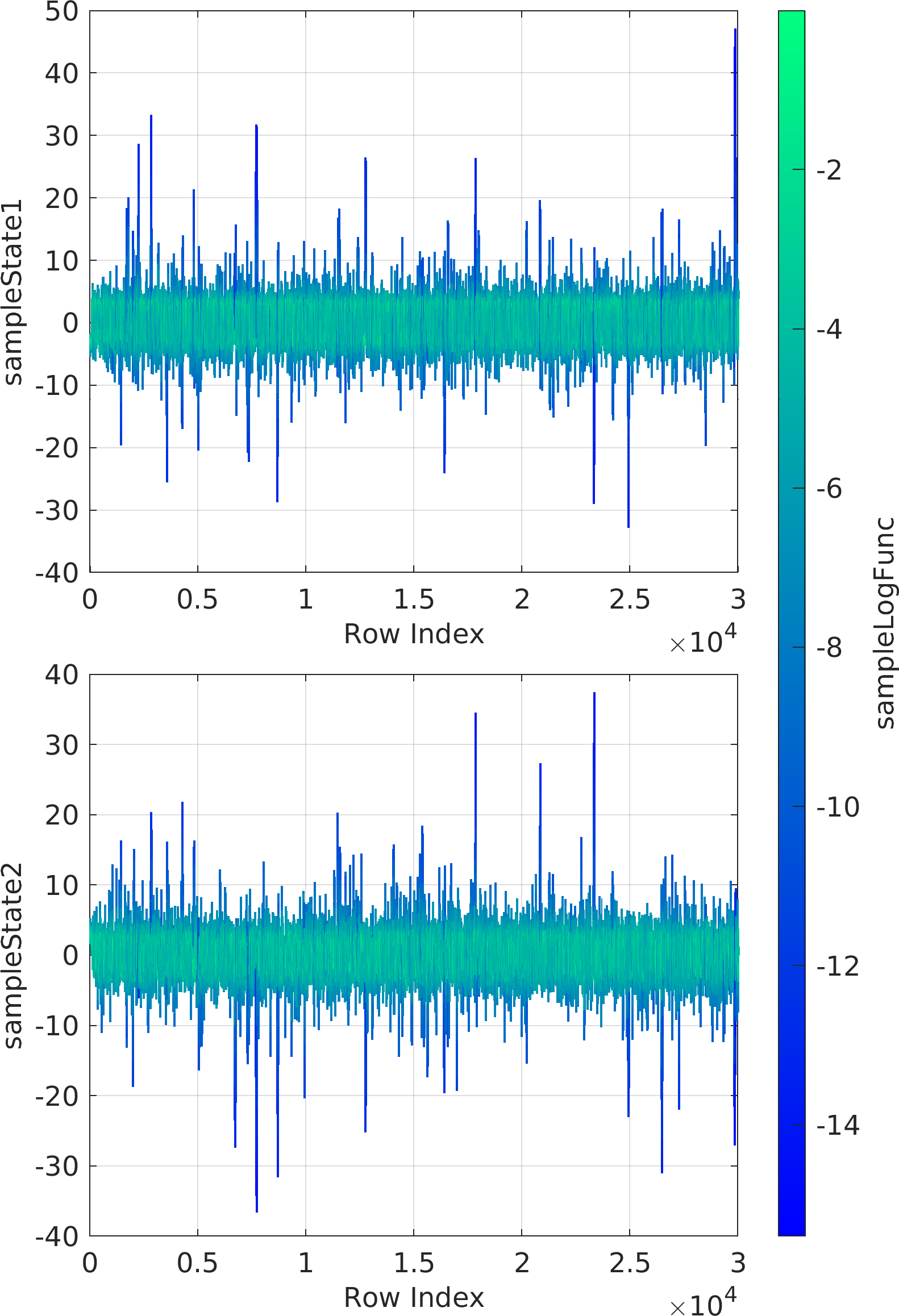
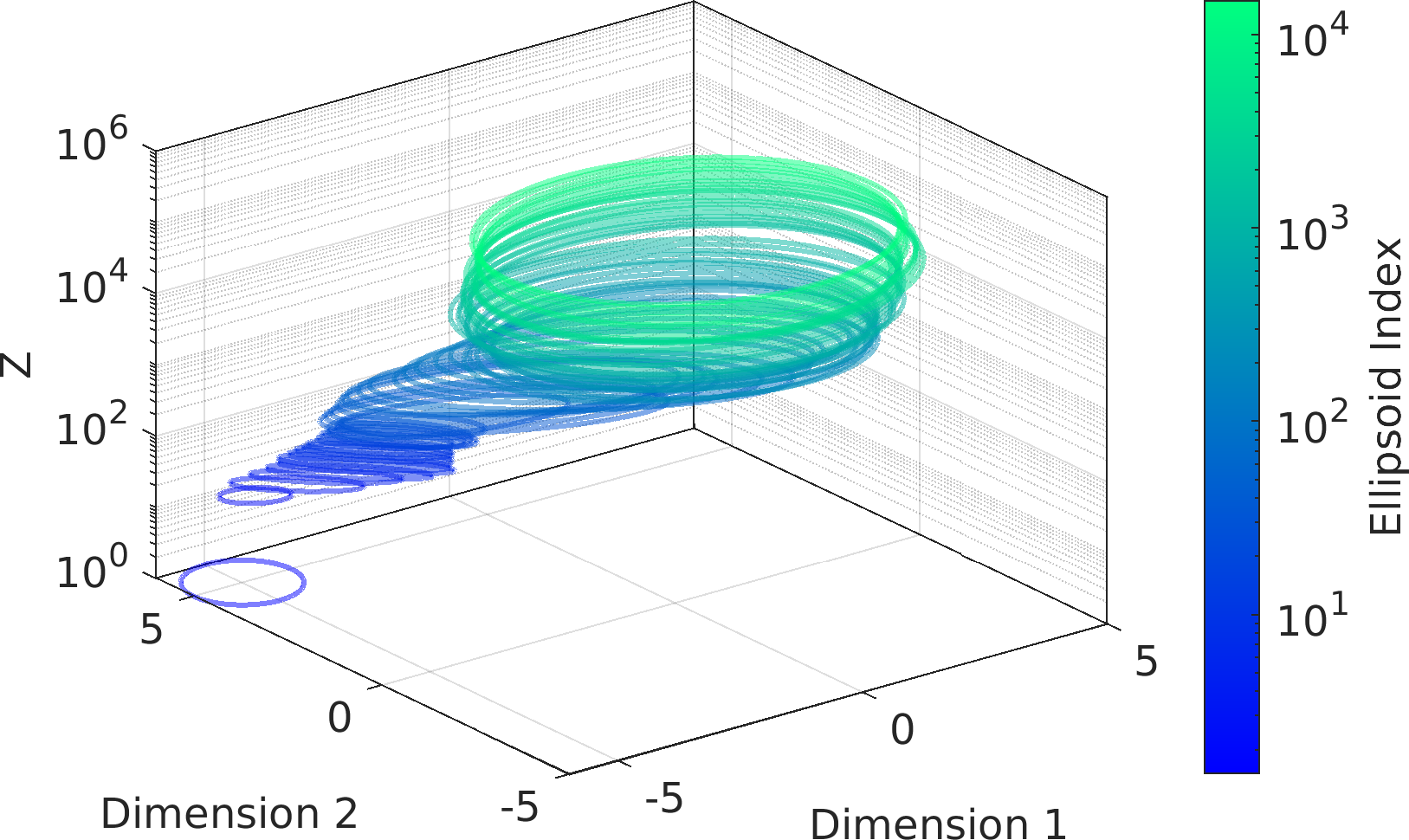
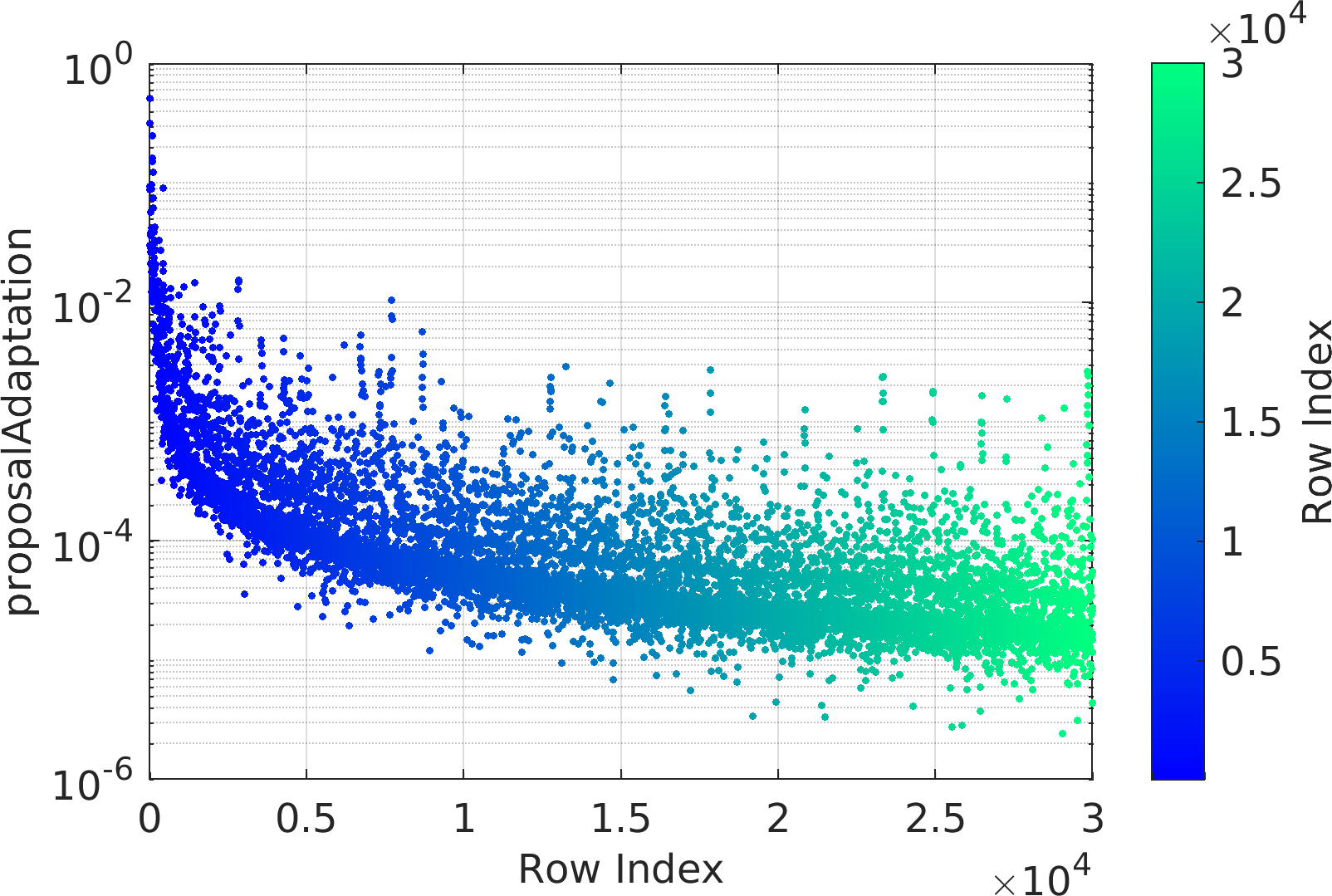
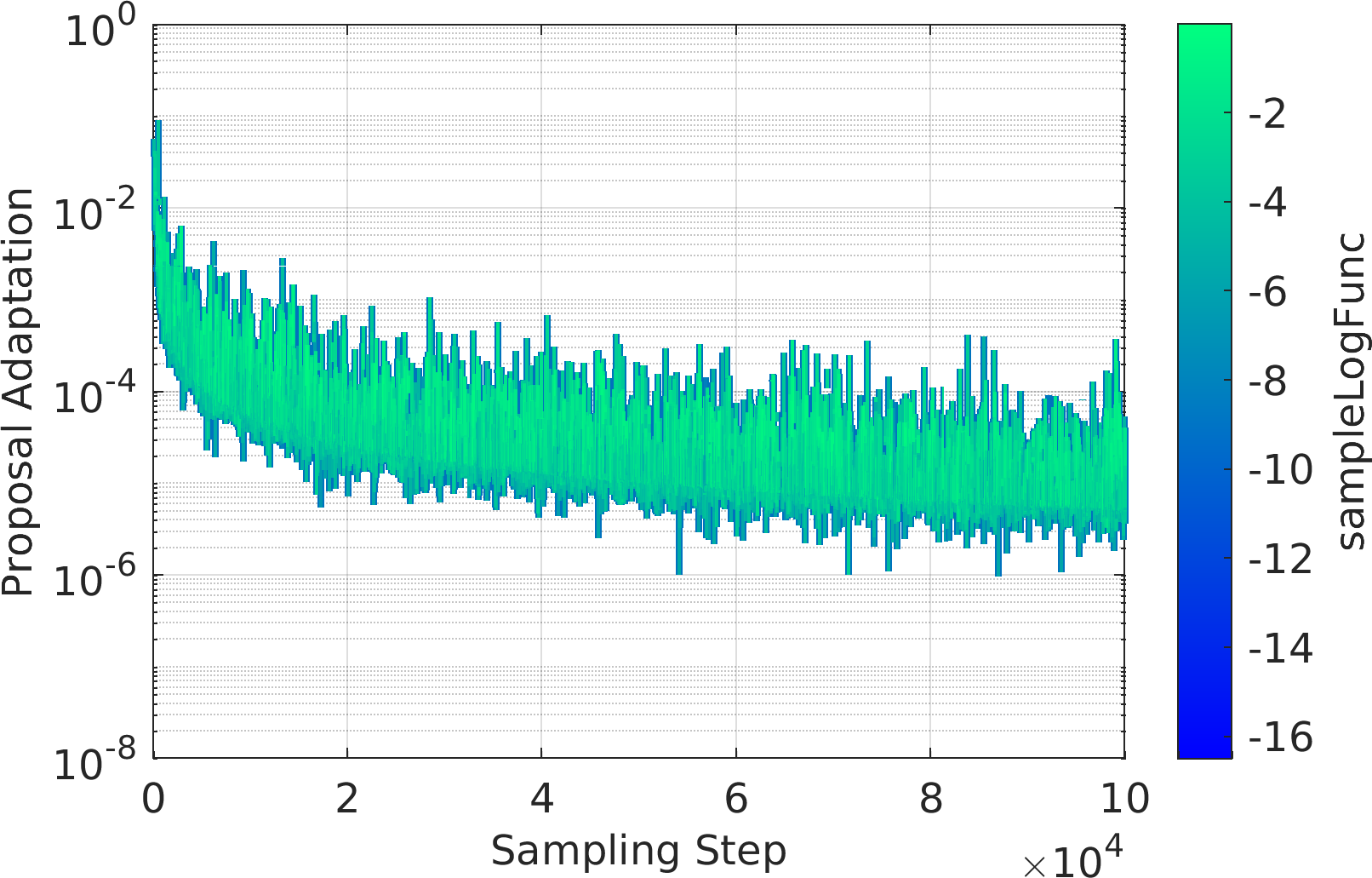
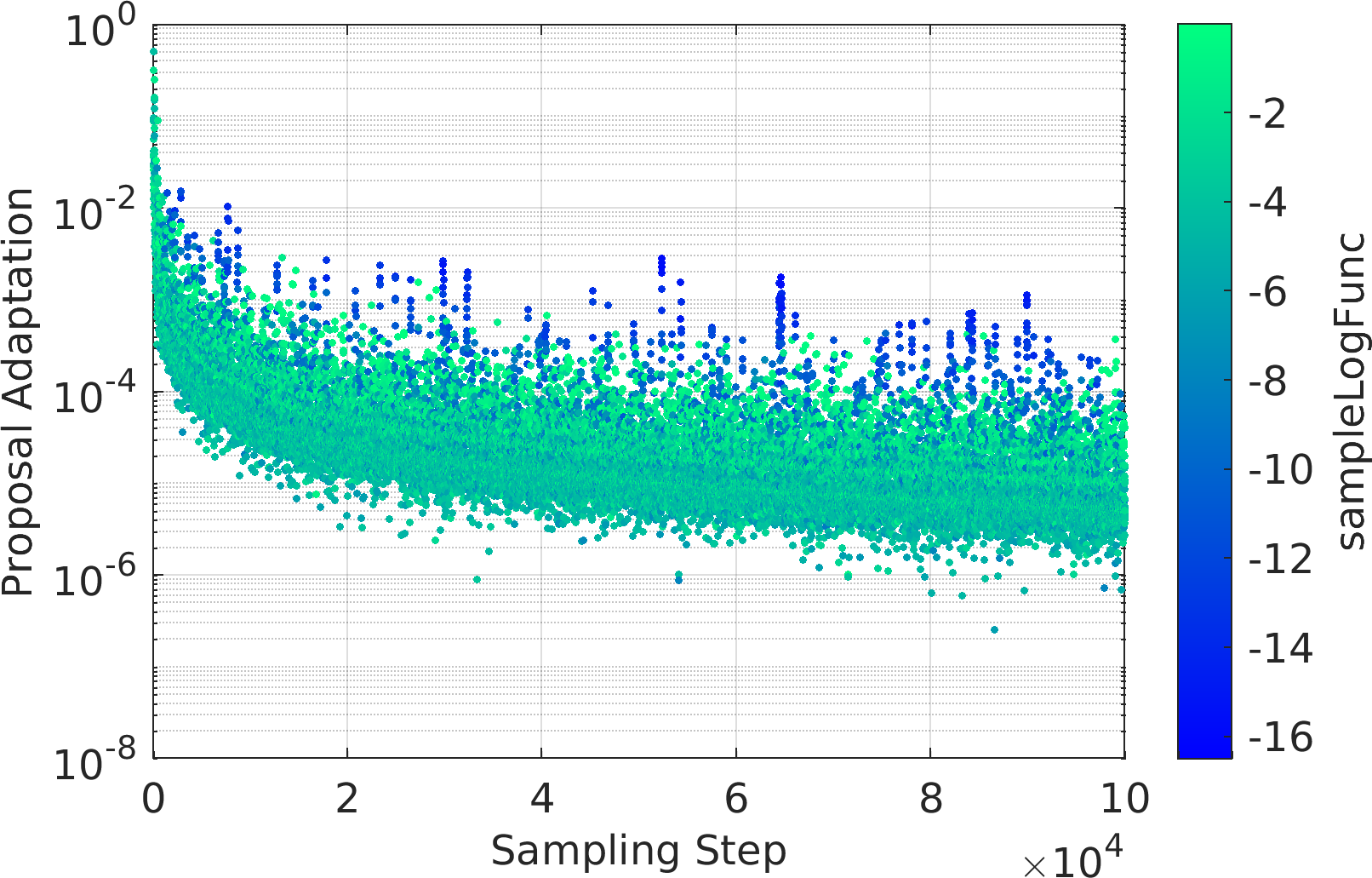
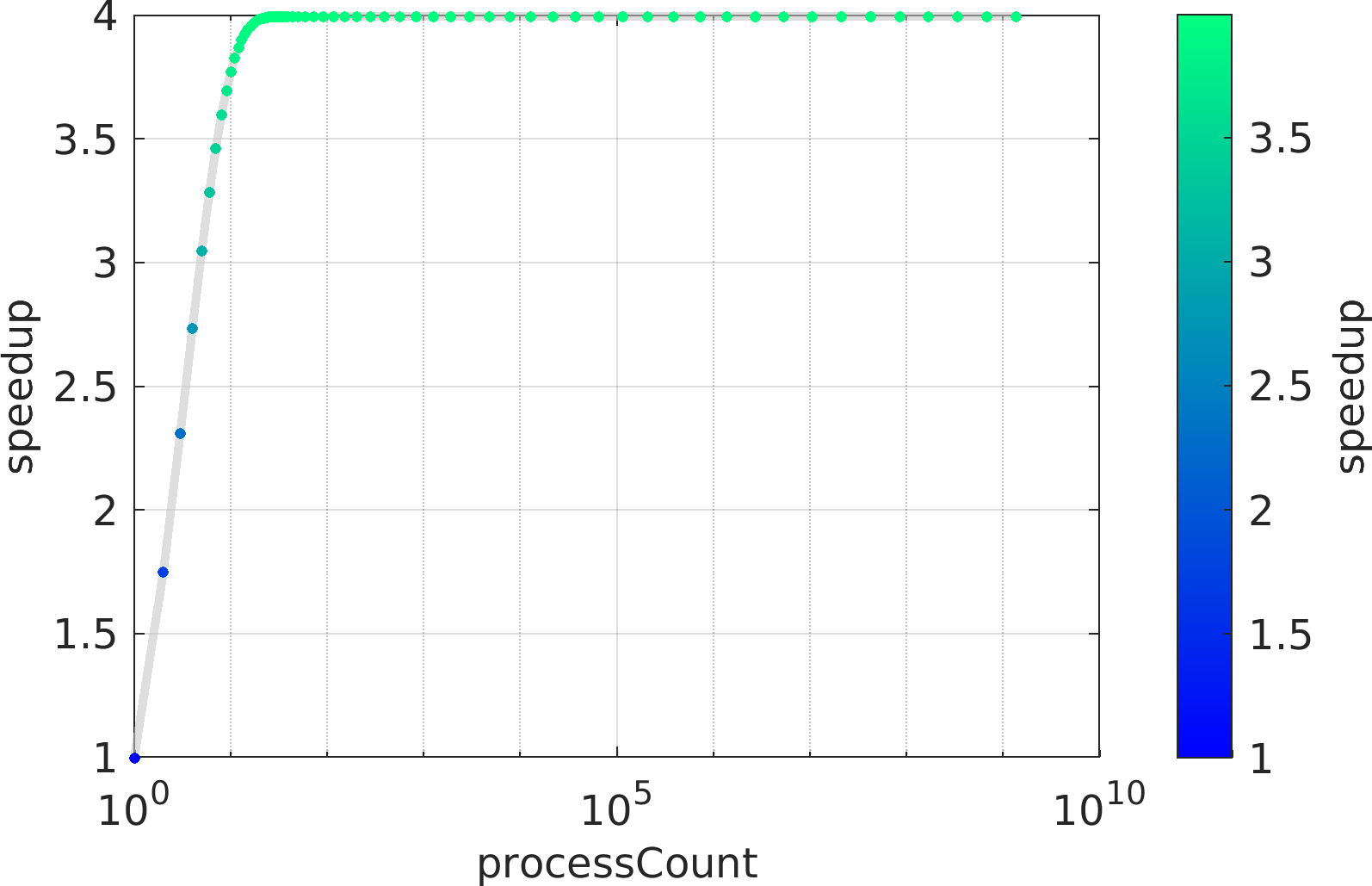
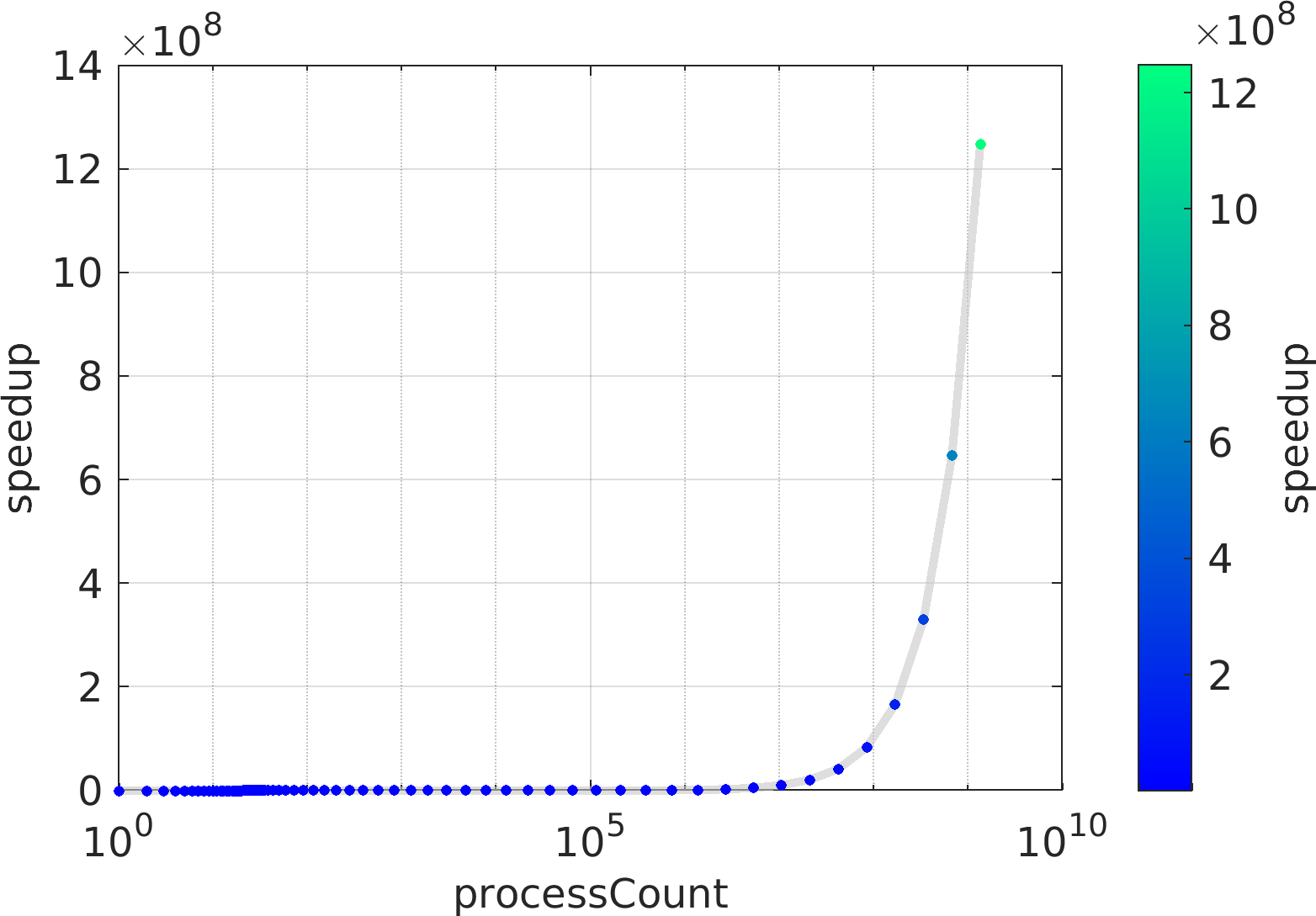
Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Amir Shahmoradi, May 16 2016, 9:03 AM, Oden Institute for Computational Engineering and Sciences (ICES), UT Austin

Member Function Documentation

◆ getppm()

function Paradram::getppm ( in  self)

Generate and return the relevant Post-Processing Message (ppm) for the current ParaMonte sampler to be displayed on the MATLAB command line after the sampling is complete.

This is a private dynamic method of the pm.sampling.Paradram sampler class.
This method is not meant to be used or accessed by the end users.

Parameters
[in]self: The input parent object of class pm.sampling.Sampler which is implicitly passed to this dynamic method (not by the user).
Note
This is an internal method of the class pm.sampling.Sampler.


Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Amir Shahmoradi, September 1, 2012, 12:00 AM, National Institute for Fusion Studies, The University of Texas at Austin%>

◆ readChainMarkov()

function Paradram::readChainMarkov ( in  self,
in  pattern,
in  sep 
)

Return a list of objects of class pm.sampling.FileContentsChainDRAM containing the content(s) of the ParaMonte simulation output chain file(s) whose path(s) match the specified input pattern or the simulation specification sampler.spec.outputFileName.

Parameters
[in]self: The input/output parent object of class pm.sampling.Paradram which is implicitly passed to this dynamic method (not by the user).
[in]pattern: See the documentation of the corresponding argument of the constructor of the method pm.sampling.Sampler.readChain.
(optional, The default is set by pm.sampling.Sampler.readChain)
[in]sep: See the documentation of the corresponding argument of the constructor of the method pm.sampling.Sampler.readChain.
(optional, The default is set by pm.sampling.Sampler.readChain)
Returns
chainMarkovList : The output cell array of objects of class pm.sampling.FileContentsChainDRAM, each of which corresponds to the contents of a unique chain file.
Try doc pm.sampling.FileContentsChainDRAM to see the documentation of the contents of the objects of the output list.


Possible calling interfaces ⛓

sampler = pm.sampling.Paradram();
chainMarkovList = sampler.readChainMarkov();
chainMarkovList = sampler.readChainMarkov([]);
chainMarkovList = sampler.readChainMarkov(file);
chainMarkovList = sampler.readChainMarkov([], []);
chainMarkovList = sampler.readChainMarkov(file, []);
chainMarkovList = sampler.readChainMarkov(file, sep);
Warning
Avoid using this routine for very large compact chains.
Reading the full Markov chain of large-scale simulation problems can be extremely memory-intensive without any potential benefits.
This method is to be only used for post-processing of the output chain file(s) of an already finished simulation. It is NOT meant to be called by all processes in parallel mode, although it is possible.
Note
This routine is identical to pm.sampling.Sampler.readChain method, except for the fact that upon reading the output chain files, it will also convert the chain contents from the default efficient compact format stored in the file to the full verbose Markov chain format.


Example usage ⛓

1cd(fileparts(mfilename('fullpath'))); % Change working directory to source code directory.
2addpath('../../../../'); % Add the ParaMonte library root directory to the search path.
3
4sampler = pm.sampling.Paradram();
5sampler.spec.outputFileName = "./out/run";
6sampler.spec.outputChainSize = 3000;
7sampler.run ( @(x) -sum((x - [-5; 5]).^2) ...
8 , 2 ...
9 );
10chain = sampler.readChainMarkov();
11chain = chain{1};
12head(chain.df)
13
14p = pm.vis.PlotScatter(chain.df, "coly", "proposalAdaptation");
15p.make("axes", {"yscale", "log"});
16p.savefig("readChainMarkov.proposalAdaptation.png", "-m3");
17
18p = pm.vis.PlotLineScatter(chain.df, "colx", chain.slfc + 1, "coly", chain.slfc + 2);
19p.make("colc", "sampleLogFunc");
20p.savefig("readChainMarkov.domain.png", "-m3");
21
22p = pm.vis.TileLine(chain.df, "tileshape", [2, 1]);
23p.make("coly", chain.slfc + [1 : 2], "colc", "sampleLogFunc");
24p.savefig("readChainMarkov.traceplot.png", "-m3");
PlotScatter
This is the PlotScatter class for generating instances of 2-dimensional Scatter Plot visualizations b...
Definition: PlotScatter.m:30
1 ParaDRAM - NOTE: Setting up the MATLAB programming language environment for a ParaDRAM simulation...
2 ParaDRAM - NOTE:
3 ParaDRAM - NOTE: The user-specified internal input file for ParaDRAM specifications detected.
4 ParaDRAM - NOTE: All ParaDRAM simulation specifications will be read from the specified internal namelist file...
5
6 ParaDRAM - NOTE: Variable `outputFileName` detected among the user-supplied specifications of the ParaDRAM sampler:
7 ParaDRAM - NOTE: "./out/run"
8 ParaDRAM - NOTE:
9 ParaDRAM - NOTE: Path to the current working directory:
10 ParaDRAM - NOTE: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov"
11 ParaDRAM - NOTE:
12 ParaDRAM - NOTE: Generating the requested directory for the ParaDRAM simulation output files:
13 ParaDRAM - NOTE: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/./out/"
14 ParaDRAM - NOTE:
15 ParaDRAM - NOTE: 1 count of preexisting complete simulation runs with the same name prefix were detected.
16 ParaDRAM - NOTE:
17 ParaDRAM - NOTE: Checking for simulation restart possibility...
18 ParaDRAM - NOTE:
19 ParaDRAM - NOTE: Starting a fresh simulation run #2 from the most recent completed simulation...
20 ParaDRAM - NOTE:
21 ParaDRAM - NOTE: Running the simulation in serial on 1 process...
22 ParaDRAM - NOTE:
23 ParaDRAM - NOTE: Generating the new output report file:
24 ParaDRAM - NOTE:
25 ParaDRAM - NOTE: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/./out/run_run2_pid1_report.txt"
26 ParaDRAM - NOTE:
27 ParaDRAM - NOTE: Please see the output *_pid1_report.txt and *_pid1_progress.txt files for further realtime simulation details...
28
29 Accepted/Total Func. Call Dynamic/Overall Acc. Rate Elapsed/Remained Time [s]
30 ========================= ========================= =========================
31
32 598 / 1000 0.5980 / 0.5980 0.0073 / 0.0292
33 1142 / 2000 0.5440 / 0.5710 0.0132 / 0.0216
34 1704 / 3000 0.5620 / 0.5680 0.0185 / 0.0141
35 2276 / 4000 0.5720 / 0.5690 0.0241 / 0.0077
36 2853 / 5000 0.5770 / 0.5706 0.0295 / 0.0015
37 3000 / 5246 0.1470 / 0.5719 0.0308 / 0.0000
38
39
40 ParaDRAM - NOTE: Computing the statistical properties of the Markov chain...
41
42 ParaDRAM - NOTE: Computing the final refined i.i.d. sample size...
43
44 ParaDRAM - NOTE: Generating the output sample file:
45 ParaDRAM - NOTE: /home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/./out/run_run2_pid1_sample.txt
46
47 ParaDRAM - NOTE: Computing the statistical properties of the final output sample...
48
49
50 ParaDRAM - NOTE: Mission Accomplished.
51
52
53Use the following object methods to read the generated basic output files:
54
55 sampler.readChain() % Return a list of the contents of the output chain file(s).
56 sampler.readSample() % Return a list of i.i.d. sample(s) from the output sample file(s).
57 sampler.readReport() % Return a list of summary report(s) from the output report file(s).
58 sampler.readRestart() % Return a list of the contents of the ASCII output restart file(s).
59 sampler.readProgress() % Return a list of the contents of the output progress file(s).
60
61Use the following object method to read the generated basic output chain file and and unroll the contents as a Markov Chain:
62
63 sampler.readChainMarkov() % Return a list of the unrolled contents of the output chain file(s) as Markov Chains.
64
65Beware that the chain unrolling significantly increases the chain size and can be very slow.
66It can potentially overflow the computer RAM for high-dimensional target density functions.
67
68For more information and examples on the usage, visit:
69
70 https://www.cdslab.org/paramonte
71
72
732 files were detected matching pattern: "./out/run"
74processing file: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/out/run_run2_pid1_chain.txt"
75reading file: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/out/run_run2_pid1_chain.txt"
76done in 0.034156 seconds.
77ncol = 9, nrow = 3000
78adding the stats components...computing the sample correlation matrix...done in 0.083452 seconds.
79computing the sample covariance matrix...done in 0.046579 seconds.
80computing the sample autocorrelation...done in 0.190520 seconds.
81done in 0.093294 seconds.
82computing the sample correlation matrix...done in 0.014132 seconds.
83computing the sample covariance matrix...done in 0.012568 seconds.
84computing the sample autocorrelation...done in 0.054122 seconds.
85adding the visualization components...done in 1.172500 seconds.
86adding the ParaDRAM-specific visualization components...adding DRAM-specific visualizations to the chain object...done in 0.050387 seconds.
87processing file: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/out/run_run1_pid1_chain.txt"
88reading file: "/home/amir/git/paramonte/external/paramonted/doxygen/bld/linux/amd64/csid/csvs/native/lib/mem/serial/matlab/checking/pkg/example/sampling/Paradram/readChainMarkov/out/run_run1_pid1_chain.txt"
89done in 0.020089 seconds.
90ncol = 9, nrow = 3000
91adding the stats components...computing the sample correlation matrix...done in 0.025462 seconds.
92computing the sample covariance matrix...done in 0.007592 seconds.
93computing the sample autocorrelation...done in 0.035119 seconds.
94done in 0.062221 seconds.
95computing the sample correlation matrix...done in 0.007201 seconds.
96computing the sample covariance matrix...done in 0.004467 seconds.
97computing the sample autocorrelation...done in 0.026844 seconds.
98adding the visualization components...done in 0.518910 seconds.
99adding the ParaDRAM-specific visualization components...adding DRAM-specific visualizations to the chain object...done in 0.066704 seconds.
100 processID delayedRejectionStage meanAcceptanceRate proposalAdaptation burninLocation sampleWeight sampleLogFunc sampleState1 sampleState2
101 _________ _____________________ __________________ __________________ ______________ ____________ _________________ ____________________ ___________________
102 1 0 0.250000009666267 0 1 1 -50 0 0
103 1 0 0.250000009666267 0 1 1 -50 0 0
104 1 0 0.250000009666267 0 1 1 -50 0 0
105 1 0 0.250000009666267 0 1 1 -50 0 0
106 1 0 0.342882473898846 0 1 1 -50.3362949891696 -0.32141397210834 -0.333584889057882
107 1 0 0.42093111931257 0.967499438460934 1 1 -50.2156223903078 -0.00626487809246379 -0.0277462070529085
108 1 0 0.42093111931257 0.967499438460934 1 1 -50.2156223903078 -0.00626487809246379 -0.0277462070529085
109 1 0 0.42093111931257 0.967499438460934 1 1 -50.2156223903078 -0.00626487809246379 -0.0277462070529085
110| 50%
111| 100% done in 0.130400 seconds.
list
function list()
Return a list of MATLAB strings containing the names of OS platforms supported by the ParaMonte MATLA...
Paradram::readChainMarkov
function readChainMarkov(in self, in pattern, in sep)
Return a list of objects of class pm.sampling.FileContentsChainDRAM containing the content(s) of the ...

Visualization of the example output ⛓





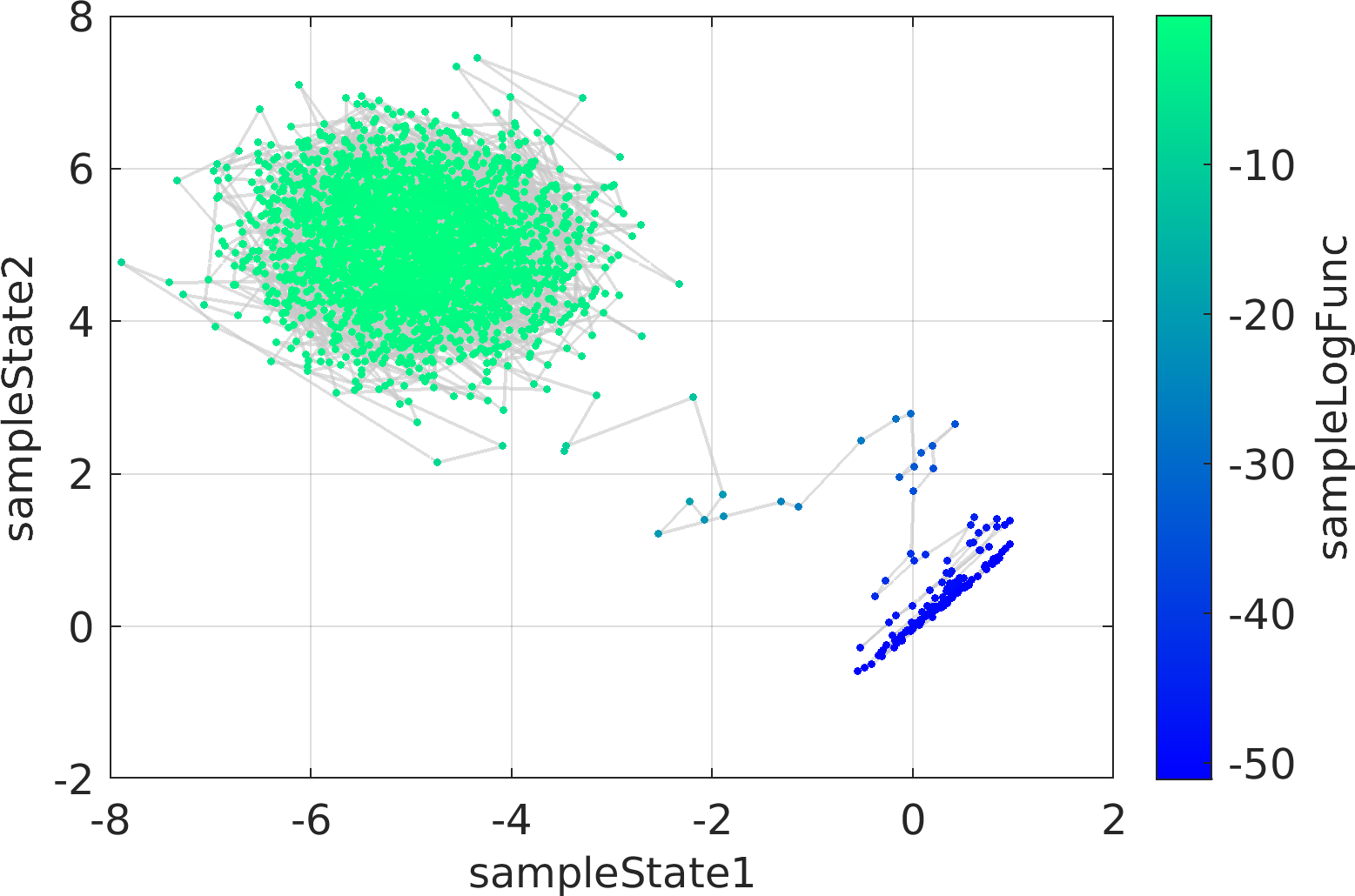
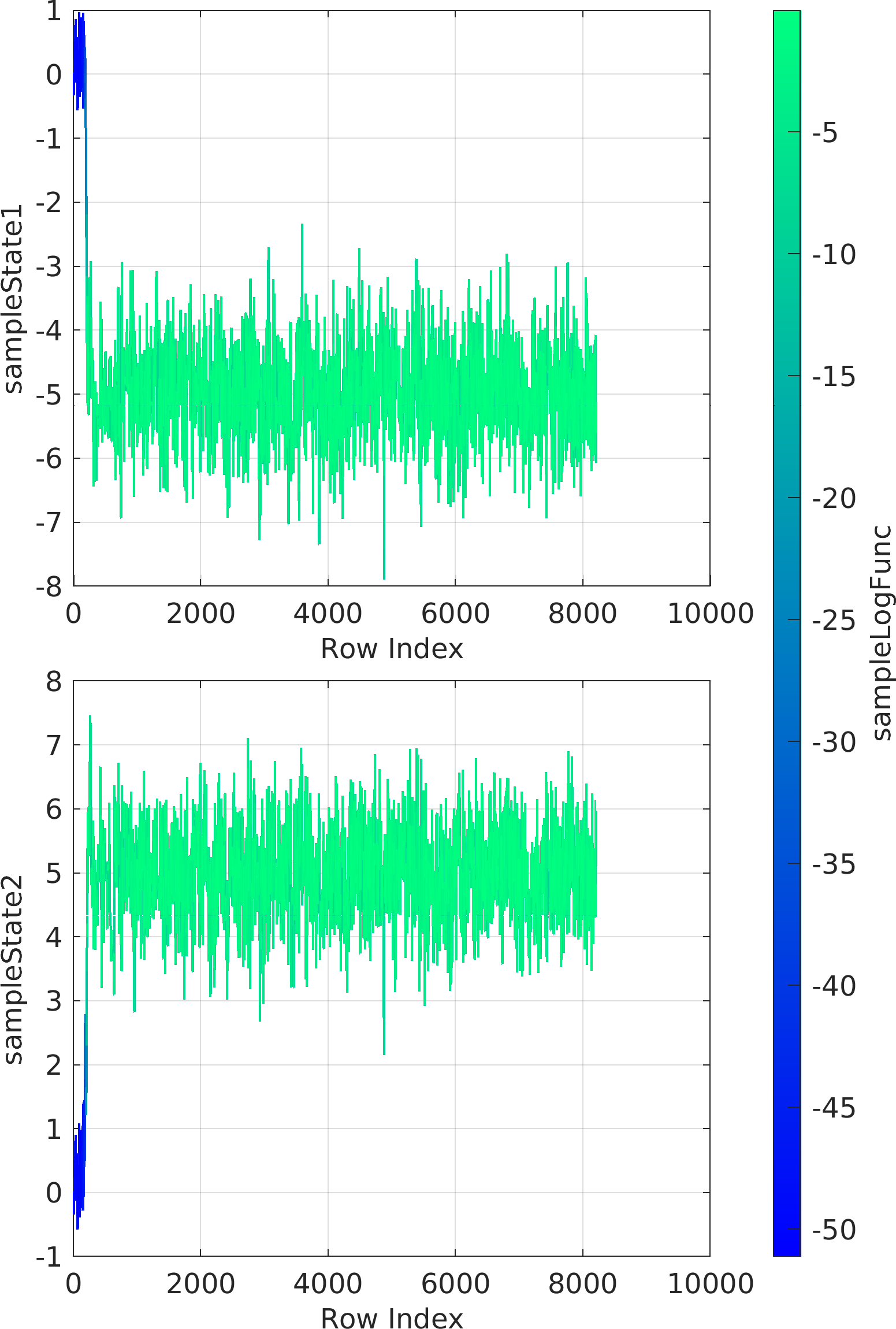
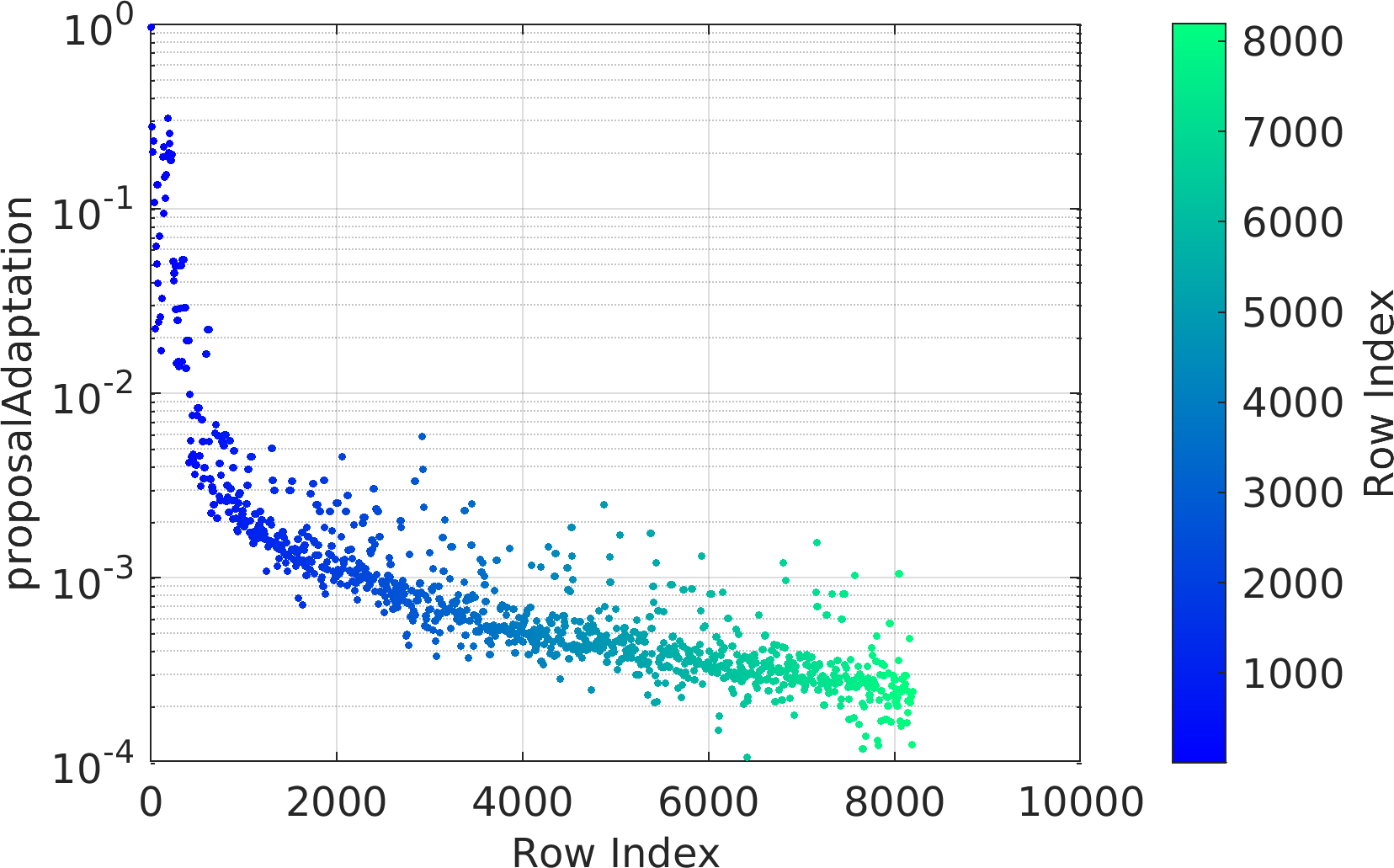
Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Joshua Alexander Osborne, May 21 2024, 12:06 AM, University of Texas at Arlington
Amir Shahmoradi, May 16 2016, 9:03 AM, Oden Institute for Computational Engineering and Sciences (ICES), UT Austin

◆ run()

function Paradram::run ( in  self,
in  getLogFunc,
in  ndim 
)

Run the ParaDRAM sampler and return nothing.

For example usage, see the documentation of the parent class of this method pm.sampler.Paradram.

Parameters
[in,out]self: The input/output parent object of class pm.sampling.Paradram which is implicitly passed to this dynamic method (not by the user).
[in]getLogFunc: The input MATLAB function handle or anonymous (lambda) function containing the implementation of the objective function to be sampled.
This user-specified function must have the following interface,
function logFunc = getLogFunc(state)
end
where,
  1. the input argument state is a vector of type MATLAB double of size ndim representing a single point from within the ndim dimensional domain of the mathematical object function to be explored.
  2. the output argument logFunc is a scalar of the same type as the input state containing the natural logarithm of the objective function at the specified input state within its domain.
[in]ndim: The input scalar positive-valued whole-number representing the number of dimensions of the domain of the user-specified objective function in the input getLogFunc().


Possible calling interfaces ⛓

sampler = pm.sampling.Paradram();
sampler.run(getLogFunc, ndim);


Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Amir Shahmoradi, September 1, 2012, 12:00 AM, National Institute for Fusion Studies, The University of Texas at Austin%>
The documentation for this class was generated from the following file: