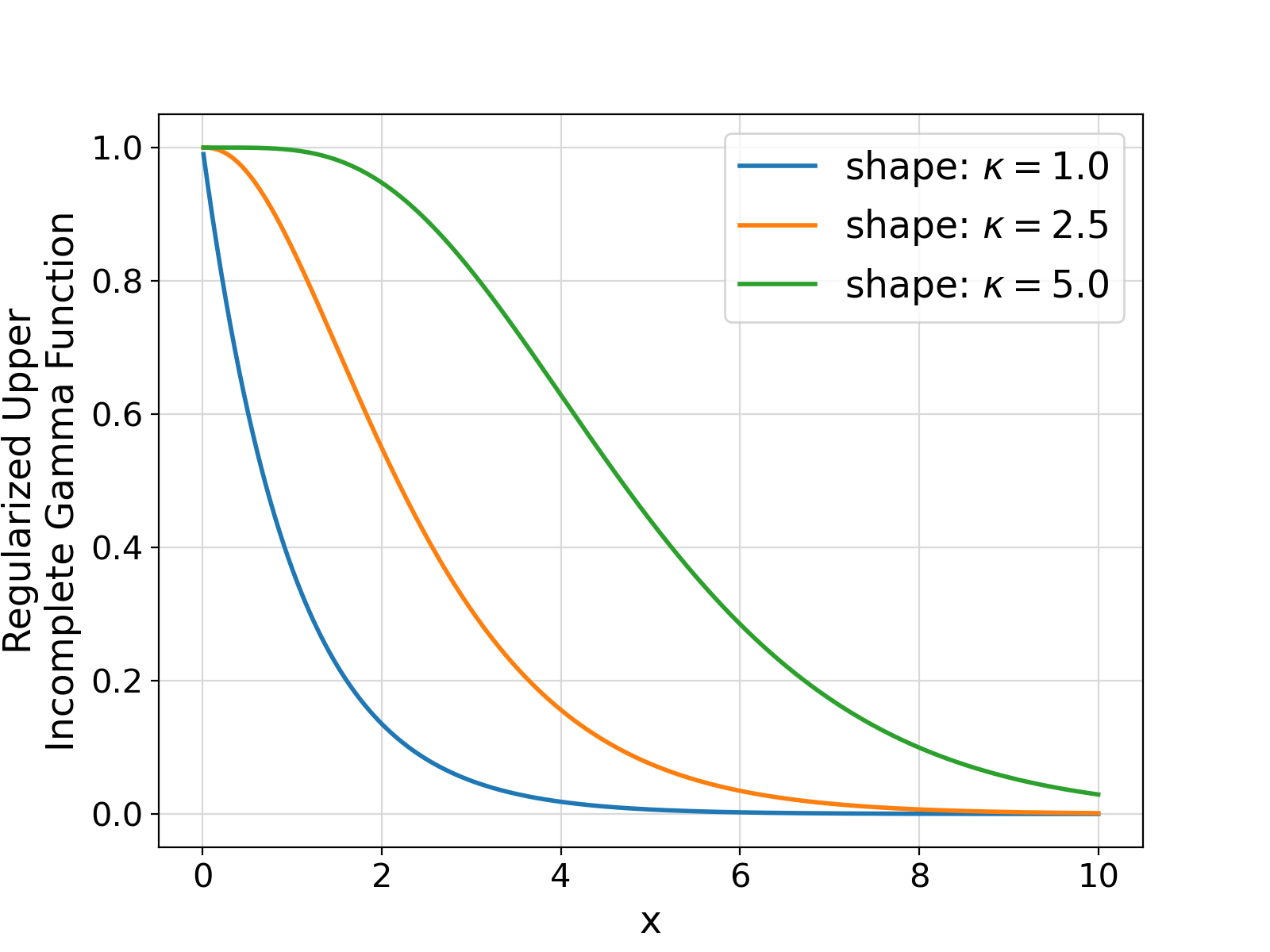
Generate and return the regularized Upper Incomplete Gamma function for the specified shape parameter ( $\kappa$) and upper limit of the integral x. More...

Detailed Description

Generate and return the regularized Upper Incomplete Gamma function for the specified shape parameter ( $\kappa$) and upper limit of the integral x.

The regularized Upper Incomplete Gamma function is defined as,

\begin{equation} \large Q(\kappa, x) = \frac{1}{\Gamma(\kappa)} \int_x^{+\infty}~t^{\kappa-1}{\mathrm e}^{-t} ~ dt ~, \end{equation}

where $(\kappa > 0, x > 0)$ should hold, with $\kappa$ representing the shape parameter of the Gamma function (or distribution) and $x$ representing the upper limit in the integral of the Upper Incomplete Gamma function.
Note that this integral is bounded between zero and one ( $[0,1]$).
The regularized Upper Incomplete Gamma function also represents the complement of the Cumulative Distribution Function (CDF) of the univariate Gamma distribution with the specified shape parameter and standardized x (with the scale parameter of unity).

Parameters

[in]	x	: The input scalar of type `real` of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), representing the upper limit in the integral of the Upper Incomplete Gamma function $Q(\kappa,x)$.
[in]	kappa	: The input scalar of the same type and kind as `x`, representing the shape parameter ( $\kappa$) of the Upper Incomplete Gamma function $Q(\kappa,x)$.

Returns: gammaIncUpp : The output scalar of the same type and kind as the output argument x representing the Upper Incomplete Gamma function for the specified kappa and upper limit.
Note that gammaIncUpp is, by definition, always positive in the range $[0, 1]$.
Note that the procedure will abruptly end the program by calling error stop if the computation of the Incomplete Gamma function fails to converge**.

Possible calling interfaces ⛓

: use pm_mathGammaGil, only: getGammaIncUppGil

gammaIncUpp = getGammaIncUppGil(x, kappa)

pm_mathGammaGil::getGammaIncUppGil
Generate and return the regularized Upper Incomplete Gamma function for the specified shape parameter...
Definition: pm_mathGammaGil.F90:273

pm_mathGammaGil
This module contains procedures and generic interfaces for the Lower and Upper Incomplete Gamma funct...
Definition: pm_mathGammaGil.F90:57

Warning: The condition 0 < x must hold for the corresponding input arguments.
The condition 0 < kappa must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

Remarks: The procedures under discussion are impure.; The procedures under discussion are elemental.

See also: getGammaIncLowGil
getGammaIncUppGil
setGammaIncGil

Example usage ⛓

: 1program example

2

3 use pm_kind, only: SK, IK, LK

4 use pm_kind, only: RKS, RKD, RKH

5 use pm_mathGammaGil, only: getGammaIncUppGil

6 use pm_io, only: display_type

7

8 implicit none

9

10 type(display_type) :: disp

11 disp = display_type(file = "main.out.F90")

12

13 call disp%skip()

14 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

15 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

16 call disp%show("! Compute the regularized Lower Incomplete Gamma Function using its series representation.")

17 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

18 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

19 call disp%skip()

20

21 call disp%skip()

22 call disp%show("getGammaIncUppGil(x = 1.5_RKS, kappa = 2._RKS)")

23 call disp%show( getGammaIncUppGil(x = 1.5_RKS, kappa = 2._RKS) )

24 call disp%skip()

25

26 call disp%skip()

27 call disp%show("getGammaIncUppGil(x = 1.5_RKD, kappa = 2._RKD)")

28 call disp%show( getGammaIncUppGil(x = 1.5_RKD, kappa = 2._RKD) )

29 call disp%skip()

30

31 call disp%skip()

32 call disp%show("getGammaIncUppGil(x = 1.5_RKH, kappa = 2._RKH)")

33 call disp%show( getGammaIncUppGil(x = 1.5_RKH, kappa = 2._RKH) )

34 call disp%skip()

35

36 call disp%skip()

37 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

38 call disp%show("! Compute the regularized Lower Incomplete Gamma Function for a vector of points.")

39 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

40 call disp%skip()

41

42 call disp%skip()

43 call disp%show("getGammaIncUppGil(x = [0._RKS, 1._RKS, 10._RKS], kappa = 2._RKS)")

44 call disp%show( getGammaIncUppGil(x = [0._RKS, 1._RKS, 10._RKS], kappa = 2._RKS) )

45 call disp%skip()

46

47 call disp%skip()

48 call disp%show("getGammaIncUppGil(x = [0._RKD, 1._RKD, 10._RKD], kappa = 2._RKD)")

49 call disp%show( getGammaIncUppGil(x = [0._RKD, 1._RKD, 10._RKD], kappa = 2._RKD) )

50 call disp%skip()

51

52 call disp%skip()

53 call disp%show("getGammaIncUppGil(x = [0._RKH, 1._RKH, 10._RKH], kappa = 2._RKH)")

54 call disp%show( getGammaIncUppGil(x = [0._RKH, 1._RKH, 10._RKH], kappa = 2._RKH) )

55 call disp%skip()

56

57 call disp%skip()

58 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

59 call disp%show("! Compute the regularized Lower Incomplete Gamma Function for a vector of shape parameters.")

60 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

61 call disp%skip()

62

63 call disp%skip()

64 call disp%show("getGammaIncUppGil(x = 1._RKS, kappa = [0.1_RKS, 1._RKS, 10._RKS])")

65 call disp%show( getGammaIncUppGil(x = 1._RKS, kappa = [0.1_RKS, 1._RKS, 10._RKS]) )

66 call disp%skip()

67

68 call disp%skip()

69 call disp%show("getGammaIncUppGil(x = 1._RKD, kappa = [0.1_RKD, 1._RKD, 10._RKD])")

70 call disp%show( getGammaIncUppGil(x = 1._RKD, kappa = [0.1_RKD, 1._RKD, 10._RKD]) )

71 call disp%skip()

72

73 call disp%skip()

74 call disp%show("getGammaIncUppGil(x = 1._RKH, kappa = [0.1_RKH, 1._RKH, 10._RKH])")

75 call disp%show( getGammaIncUppGil(x = 1._RKH, kappa = [0.1_RKH, 1._RKH, 10._RKH]) )

76 call disp%skip()

77

78 call disp%skip()

79 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

80 call disp%show("! Compute the regularized Lower Incomplete Gamma Function for a vector of points and shape parameters.")

81 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

82 call disp%skip()

83

84 block

85 use pm_kind, only: RKG => RKS

86 integer(IK) :: i, rprecision

87 integer(IK), allocatable :: exprange(:), info(:)

88 real(RKG), allocatable :: gamIncLow(:)

89 call disp%skip()

90 call disp%show("rprecision = precision(0._RKG) * 2")

91 rprecision = precision(0._RKG) * 2

92 call disp%show("rprecision")

93 call disp%show( rprecision )

94 call disp%show("exprange = [(i, i = -rprecision, rprecision)]")

95 exprange = [(i, i = -rprecision, rprecision)]

96 call disp%show("exprange")

97 call disp%show( exprange )

98 call disp%show("allocate(gamIncLow(size(exprange)), info(size(exprange)))")

99 allocate(gamIncLow(size(exprange)), info(size(exprange)))

100 call disp%show("gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)")

101 gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)

102 call disp%show("reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2])")

103 call disp%show( reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2]) )

104 call disp%skip()

105 end block

106

107 block

108 use pm_kind, only: RKG => RKD

109 integer(IK) :: i, rprecision

110 integer(IK), allocatable :: exprange(:), info(:)

111 real(RKG), allocatable :: gamIncLow(:)

112 call disp%skip()

113 call disp%show("rprecision = precision(0._RKG) * 2")

114 rprecision = precision(0._RKG) * 2

115 call disp%show("rprecision")

116 call disp%show( rprecision )

117 call disp%show("exprange = [(i, i = -rprecision, rprecision)]")

118 exprange = [(i, i = -rprecision, rprecision)]

119 call disp%show("exprange")

120 call disp%show( exprange )

121 call disp%show("allocate(gamIncLow(size(exprange)), info(size(exprange)))")

122 allocate(gamIncLow(size(exprange)), info(size(exprange)))

123 call disp%show("gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)")

124 gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)

125 call disp%show("reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2])")

126 call disp%show( reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2]) )

127 call disp%skip()

128 end block

129

130 block

131 use pm_kind, only: RKG => RKH

132 integer(IK) :: i, rprecision

133 integer(IK), allocatable :: exprange(:), info(:)

134 real(RKG), allocatable :: gamIncLow(:)

135 call disp%skip()

136 call disp%show("rprecision = precision(0._RKG) * 2")

137 rprecision = precision(0._RKG) * 2

138 call disp%show("rprecision")

139 call disp%show( rprecision )

140 call disp%show("exprange = [(i, i = -rprecision, rprecision)]")

141 exprange = [(i, i = -rprecision, rprecision)]

142 call disp%show("exprange")

143 call disp%show( exprange )

144 call disp%show("allocate(gamIncLow(size(exprange)), info(size(exprange)))")

145 allocate(gamIncLow(size(exprange)), info(size(exprange)))

146 call disp%show("gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)")

147 gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)

148 call disp%show("reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2])")

149 call disp%show( reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2]) )

150 call disp%skip()

151 end block

152

153 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

154 ! Output an example array of the regularized Lower Incomplete Gamma function for visualization.

155 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

156

157 block

158

159 use pm_arraySpace, only: setLinSpace

160 integer(IK) , parameter :: NP = 1000_IK

161 real(RKS) :: x_RKS(NP)

162 integer :: fileUnit, i

163

164 call setLinSpace(x_RKS, 0._RKS, 10._RKS)

165 open(newunit = fileUnit, file = "getGammaIncUppGil.RK.txt")

166 do i = 1, NP

167 write(fileUnit, "(*(g0,:,' '))") x_RKS(i), getGammaIncUppGil(x_RKS(i), kappa = [1.0_RKS, 2.5_RKS, 5.0_RKS])

168 end do

169 close(fileUnit)

170

171 end block

172

173end program example

pm_arraySpace::setLinSpace
Return the linSpace output argument with size(linSpace) elements of evenly-spaced values over the int...
Definition: pm_arraySpace.F90:324

pm_io::show
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11726

pm_io::skip
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11508

pm_arraySpace
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
Definition: pm_arraySpace.F90:33

pm_io
This module contains classes and procedures for input/output (IO) or generic display operations on st...
Definition: pm_io.F90:252

pm_io::disp
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
Definition: pm_io.F90:11393

pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268

pm_kind::LK
integer, parameter LK
The default logical kind in the ParaMonte library: kind(.true.) in Fortran, kind(....
Definition: pm_kind.F90:541

pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540

pm_kind::RKD
integer, parameter RKD
The double precision real kind in Fortran mode. On most platforms, this is an 64-bit real kind.
Definition: pm_kind.F90:568

pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539

pm_kind::RKH
integer, parameter RKH
The scalar integer constant of intrinsic default kind, representing the highest-precision real kind t...
Definition: pm_kind.F90:858

pm_kind::RKS
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Definition: pm_kind.F90:567

pm_io::display_type
Generate and return an object of type display_type.
Definition: pm_io.F90:10282

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe

2set PATH=..\..\..\lib;%PATH%

3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe

4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example output ⛓
1

2!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

3!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

4! Compute the regularized Lower Incomplete Gamma Function using its series representation.

5!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

6!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

7

8

9getGammaIncUppGil(x = 1.5_RKS, kappa = 2._RKS)

10+0.557825565

11

12

13getGammaIncUppGil(x = 1.5_RKD, kappa = 2._RKD)

14+0.55782540037107464

15

16

17getGammaIncUppGil(x = 1.5_RKH, kappa = 2._RKH)

18+0.557825400371074572333201176910031393

19

20

21!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

22! Compute the regularized Lower Incomplete Gamma Function for a vector of points.

23!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

24

25

26getGammaIncUppGil(x = [0._RKS, 1._RKS, 10._RKS], kappa = 2._RKS)

27+1.00000000, +0.735758901, +0.499399204E-3

28

29

30getGammaIncUppGil(x = [0._RKD, 1._RKD, 10._RKD], kappa = 2._RKD)

31+1.0000000000000000, +0.73575888234288467, +0.49939922738733355E-3

32

33

34getGammaIncUppGil(x = [0._RKH, 1._RKH, 10._RKH], kappa = 2._RKH)

35+1.00000000000000000000000000000000000, +0.735758882342884643191047540322921938, +0.499399227387333366891506671166056614E-3

36

37

38!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

39! Compute the regularized Lower Incomplete Gamma Function for a vector of shape parameters.

40!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

41

42

43getGammaIncUppGil(x = 1._RKS, kappa = [0.1_RKS, 1._RKS, 10._RKS])

44+0.241273157E-1, +0.367879450, +0.999999881

45

46

47getGammaIncUppGil(x = 1._RKD, kappa = [0.1_RKD, 1._RKD, 10._RKD])

48+0.24127343726327577E-1, +0.36787944117144233, +0.99999988857452171

49

50

51getGammaIncUppGil(x = 1._RKH, kappa = [0.1_RKH, 1._RKH, 10._RKH])

52+0.241273437263277773829694356333546198E-1, +0.367879441171442321595523770161460873, +0.999999888574521661279322646951801396

53

54

55!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

56! Compute the regularized Lower Incomplete Gamma Function for a vector of points and shape parameters.

57!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

58

59

60rprecision = precision(0._RKG) * 2

61rprecision

62+12

63exprange = [(i, i = -rprecision, rprecision)]

64exprange

65-12, -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, +0, +1, +2, +3, +4, +5, +6, +7, +8, +9, +10, +11, +12

66allocate(gamIncLow(size(exprange)), info(size(exprange)))

67gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)

68reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2])

69+0.999999996E-12, +0.270538054E-10

70+0.999999996E-11, +0.247512205E-9

71+0.100000001E-9, +0.224486341E-8

72+0.999999972E-9, +0.201460502E-7

73+0.999999994E-8, +0.178434632E-6

74+0.100000001E-6, +0.155408668E-5

75+0.999999997E-6, +0.132382092E-4

76+0.999999975E-5, +0.109351291E-3

77+0.999999975E-4, +0.862958201E-3

78+0.100000005E-2, +0.631235354E-2

79+0.999999978E-2, +0.396525711E-1

80+0.100000001, +0.172448233

81+1.00000000, +0.367879450

82+10.0000000, +0.457929730

83+100.000000, +0.486701190

84+1000.00000, +0.495794743

85+10000.0000, +0.498670191

86+100000.000, +0.499579489

87+1000000.00, +0.499867022

88+10000000.0, +0.499957949

89+100000000., +0.499986708

90+0.100000000E+10, +0.499995798

91+0.100000000E+11, +0.499998659

92+0.999999980E+11, +0.499999583

93+0.999999996E+12, +0.499999881

94

95

96rprecision = precision(0._RKG) * 2

97rprecision

98+30

99exprange = [(i, i = -rprecision, rprecision)]

100exprange

101-30, -29, -28, -27, -26, -25, -24, -23, -22, -21, -20, -19, -18, -17, -16, -15, -14, -13, -12, -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, +0, +1, +2, +3, +4, +5, +6, +7, +8, +9, +10, +11, +12, +13, +14, +15, +16, +17, +18, +19, +20, +21, +22, +23, +24, +25, +26, +27, +28, +29, +30

102allocate(gamIncLow(size(exprange)), info(size(exprange)))

103gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)

104reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2])

105+0.99999999999999991E-30, +0.68500337124919835E-28

106+0.10000000000000001E-28, +0.66197752031925787E-27

107+0.10000000000000001E-27, +0.63895166938931759E-26

108+0.10000000000000000E-26, +0.61592581845937708E-25

109+0.99999999999999990E-26, +0.59289996752943643E-24

110+0.99999999999999992E-25, +0.56987411659949602E-23

111+0.10000000000000001E-23, +0.54684826566955573E-22

112+0.10000000000000001E-22, +0.52382241473961525E-21

113+0.10000000000000000E-21, +0.50079656380967482E-20

114+0.99999999999999991E-21, +0.47777071287973421E-19

115+0.99999999999999995E-20, +0.45474486194979385E-18

116+0.99999999999999998E-19, +0.43171901101985335E-17

117+0.10000000000000001E-17, +0.40869316008991295E-16

118+0.10000000000000001E-16, +0.38566730915997240E-15

119+0.99999999999999998E-16, +0.36264145823003133E-14

120+0.10000000000000001E-14, +0.33961560730008585E-13

121+0.10000000000000000E-13, +0.31658975637010116E-12

122+0.10000000000000000E-12, +0.29356390543978156E-11

123+0.99999999999999998E-12, +0.27053805450662883E-10

124+0.99999999999999994E-11, +0.24751220354988079E-9

125+0.10000000000000000E-9, +0.22448635240024114E-8

126+0.10000000000000001E-8, +0.20146049970935676E-7

127+0.10000000000000000E-7, +0.17843463505329364E-6

128+0.99999999999999995E-7, +0.15540868092361909E-5

129+0.99999999999999995E-6, +0.13238209089664834E-4

130+0.10000000000000001E-4, +0.10935130095632985E-3

131+0.10000000000000000E-3, +0.86295813100659982E-3

132+0.10000000000000000E-2, +0.63123532911397084E-2

133+0.10000000000000000E-1, +0.39652576478490797E-1

134+0.10000000000000001, +0.17244824041414941

135+1.0000000000000000, +0.36787944117144233

136+10.000000000000000, +0.45792971447185232

137+100.00000000000000, +0.48670120172085135

138+1000.0000000000000, +0.49579475581978449

139+10000.000000000000, +0.49867019166004478

140+100000.00000000000, +0.49957947788963480

141+1000000.0000000000, +0.49986701923912741

142+10000000.000000000, +0.49995794779127628

143+100000000.00000000, +0.49998670192398587

144+1000000000.0000000, +0.49999579477912992

145+10000000000.000000, +0.49999867019239869

146+100000000000.00000, +0.49999957947791301

147+1000000000000.0000, +0.49999986701923987

148+10000000000000.000, +0.49999995794779128

149+100000000000000.00, +0.49999998670192397

150+1000000000000000.0, +0.49999999579477911

151+10000000000000000., +0.49999999867019240

152+0.10000000000000000E+18, +0.49999999957947794

153+0.10000000000000000E+19, +0.49999999986701926

154+0.10000000000000000E+20, +0.49999999995794780

155+0.10000000000000000E+21, +0.49999999998670192

156+0.10000000000000000E+22, +0.49999999999579475

157+0.10000000000000000E+23, +0.49999999999867017

158+0.99999999999999992E+23, +0.49999999999957950

159+0.99999999999999998E+24, +0.49999999999986700

160+0.10000000000000001E+26, +0.49999999999995792

161+0.10000000000000000E+27, +0.49999999999998668

162+0.10000000000000000E+28, +0.49999999999999578

163+0.99999999999999996E+28, +0.49999999999999867

164+0.99999999999999991E+29, +0.49999999999999956

165+0.10000000000000000E+31, +0.49999999999999989

166

167

168rprecision = precision(0._RKG) * 2

169rprecision

170+66

171exprange = [(i, i = -rprecision, rprecision)]

172exprange

173-66, -65, -64, -63, -62, -61, -60, -59, -58, -57, -56, -55, -54, -53, -52, -51, -50, -49, -48, -47, -46, -45, -44, -43, -42, -41, -40, -39, -38, -37, -36, -35, -34, -33, -32, -31, -30, -29, -28, -27, -26, -25, -24, -23, -22, -21, -20, -19, -18, -17, -16, -15, -14, -13, -12, -11, -10, -9, -8, -7, -6, -5, -4, -3, -2, -1, +0, +1, +2, +3, +4, +5, +6, +7, +8, +9, +10, +11, +12, +13, +14, +15, +16, +17, +18, +19, +20, +21, +22, +23, +24, +25, +26, +27, +28, +29, +30, +31, +32, +33, +34, +35, +36, +37, +38, +39, +40, +41, +42, +43, +44, +45, +46, +47, +48, +49, +50, +51, +52, +53, +54, +55, +56, +57, +58, +59, +60, +61, +62, +63, +64, +65, +66

174allocate(gamIncLow(size(exprange)), info(size(exprange)))

175gamIncLow = getGammaIncUppGil(x = 10._RKG**exprange, kappa = 10._RKG**exprange)

176reshape([10._RKG**exprange, gamIncLow], shape = [size(info), 2])

177+0.100000000000000000000000000000000475E-65, +0.151393400472705482284580816009168751E-63

178+0.100000000000000000000000000000000468E-64, +0.149090815379711436600562824554484351E-62

179+0.100000000000000000000000000000000457E-63, +0.146788230286717390916544833099799978E-61

180+0.100000000000000000000000000000000451E-62, +0.144485645193723345232526841645115591E-60

181+0.100000000000000000000000000000000463E-61, +0.142183060100729299548508850190431224E-59

182+0.100000000000000000000000000000000444E-60, +0.139880475007735253864490858735746841E-58

183+0.100000000000000000000000000000000432E-59, +0.137577889914741208180472867281062446E-57

184+0.100000000000000000000000000000000420E-58, +0.135275304821747162496454875826378056E-56

185+0.100000000000000000000000000000000412E-57, +0.132972719728753116812436884371693649E-55

186+0.100000000000000000000000000000000409E-56, +0.130670134635759071128418892917009297E-54

187+0.100000000000000000000000000000000395E-55, +0.128367549542765025444400901462324887E-53

188+0.100000000000000000000000000000000381E-54, +0.126064964449770979760382910007640505E-52

189+0.100000000000000000000000000000000397E-53, +0.123762379356776934076364918552956150E-51

190+0.100000000000000000000000000000000384E-52, +0.121459794263782888392346927098271768E-50

191+0.100000000000000000000000000000000378E-51, +0.119157209170788842708328935643587391E-49

192+0.100000000000000000000000000000000365E-50, +0.116854624077794797024310944188902994E-48

193+0.100000000000000000000000000000000355E-49, +0.114552038984800751340292952734218611E-47

194+0.100000000000000000000000000000000353E-48, +0.112249453891806705656274961279534232E-46

195+0.100000000000000000000000000000000346E-47, +0.109946868798812659972256969824849863E-45

196+0.100000000000000000000000000000000333E-46, +0.107644283705818614288238978370165480E-44

197+0.100000000000000000000000000000000339E-45, +0.105341698612824568604220986915481101E-43

198+0.100000000000000000000000000000000336E-44, +0.103039113519830522920202995460796726E-42

199+0.100000000000000000000000000000000328E-43, +0.100736528426836477236185004006112357E-41

200+0.100000000000000000000000000000000304E-42, +0.984339433338424315521670125514279610E-41

201+0.100000000000000000000000000000000301E-41, +0.961313582408483858681490210967435857E-40

202+0.100000000000000000000000000000000301E-40, +0.938287731478543401841310296420592078E-39

203+0.100000000000000000000000000000000296E-39, +0.915261880548602945001130381873748355E-38

204+0.100000000000000000000000000000000268E-38, +0.892236029618662488160950467326904439E-37

205+0.100000000000000000000000000000000276E-37, +0.869210178688722031320770552780060732E-36

206+0.100000000000000000000000000000000265E-36, +0.846184327758781574480590638233216967E-35

207+0.100000000000000000000000000000000269E-35, +0.823158476828841117640410723686373295E-34

208+0.100000000000000000000000000000000246E-34, +0.800132625898900660800230809139529094E-33

209+0.100000000000000000000000000000000239E-33, +0.777106774968960203960050894592682571E-32

210+0.100000000000000000000000000000000242E-32, +0.754080924039019747119870980045813633E-31

211+0.100000000000000000000000000000000230E-31, +0.731055073109079290279691065498731087E-30

212+0.100000000000000000000000000000000216E-30, +0.708029222179138833439511150949649743E-29

213+0.100000000000000000000000000000000228E-29, +0.685003371249198376599331236381867661E-28

214+0.100000000000000000000000000000000212E-28, +0.661977520319257919759151321639542213E-27

215+0.100000000000000000000000000000000208E-27, +0.638951669389317462918971405272149574E-26

216+0.100000000000000000000000000000000196E-26, +0.615925818459377006078791473814773565E-25

217+0.100000000000000000000000000000000187E-25, +0.592899967529436549238611402634996683E-24

218+0.100000000000000000000000000000000177E-24, +0.569874116599496092398430041711015107E-23

219+0.100000000000000000000000000000000169E-23, +0.546848265669555635558236815197635388E-22

220+0.100000000000000000000000000000000153E-22, +0.523822414739615178717934821863015986E-21

221+0.100000000000000000000000000000000165E-21, +0.500796563809674721876639756505976475E-20

222+0.100000000000000000000000000000000151E-20, +0.477770712879734265026316987449770937E-19

223+0.100000000000000000000000000000000145E-19, +0.454744861949793808094317892905347267E-18

224+0.100000000000000000000000000000000132E-18, +0.431719011019853350427268121043652516E-17

225+0.100000000000000000000000000000000129E-17, +0.408693160089912886183891976963468882E-16

226+0.100000000000000000000000000000000119E-16, +0.385667309159972363489602373291883113E-15

227+0.100000000000000000000000000000000114E-15, +0.362641458230031325115143330154250467E-14

228+0.100000000000000000000000000000000101E-14, +0.339615607300085775283266762009474174E-13

229+0.100000000000000000000000000000000108E-13, +0.316589756370101134866236695492265302E-12

230+0.100000000000000000000000000000000100E-12, +0.293563905439781533950419984777655021E-11

231+0.100000000000000000000000000000000096E-11, +0.270538054506628836199549412406132086E-10

232+0.100000000000000000000000000000000075E-10, +0.247512203549880797881140420122824513E-9

233+0.100000000000000000000000000000000072E-9, +0.224486352400241094382072745933450478E-8

234+0.100000000000000000000000000000000065E-8, +0.201460499709356778860956702317862944E-7

235+0.100000000000000000000000000000000058E-7, +0.178434635053293640783838263014790580E-6

236+0.100000000000000000000000000000000043E-6, +0.155408680923619091775018793645288755E-5

237+0.100000000000000000000000000000000048E-5, +0.132382090896648326218820773011159595E-4

238+0.100000000000000000000000000000000041E-4, +0.109351300956329854758267514478738720E-3

239+0.100000000000000000000000000000000032E-3, +0.862958131006599938564443167898102556E-3

240+0.100000000000000000000000000000000013E-2, +0.631235329113970979344124959671627705E-2

241+0.100000000000000000000000000000000017E-1, +0.396525764784908016731172845462856462E-1

242+0.100000000000000000000000000000000005, +0.172448240414149458549687610255856491

243+1.00000000000000000000000000000000000, +0.367879441171442321595523770161460873

244+10.0000000000000000000000000000000000, +0.457929714471852208314154629345237310

245+100.000000000000000000000000000000000, +0.486701201720851335142685743439263212

246+1000.00000000000000000000000000000000, +0.495794755819784491496222156397881186

247+10000.0000000000000000000000000000000, +0.498670191660044799617257748700148614

248+100000.000000000000000000000000000000, +0.499579477889634823306687420956173711

249+1000000.00000000000000000000000000000, +0.499867019239127408755677182496793271

250+10000000.0000000000000000000000000000, +0.499957947791276301666243835215974015

251+100000000.000000000000000000000000000, +0.499986701923985880128751082407172848

252+1000000000.00000000000000000000000000, +0.499995794779129943037581473378871871

253+10000000000.0000000000000000000000000, +0.499998670192398661152291532934646396

254+100000000000.000000000000000000000000, +0.499999579477912996616629620642081067

255+1000000000000.00000000000000000000000, +0.499999867019239866188368571350571611

256+10000000000000.0000000000000000000000, +0.499999957947791299663975833542674431

257+100000000000000.000000000000000000000, +0.499999986701923986618909996553130608

258+1000000000000000.00000000000000000000, +0.499999995794779129966399896225745970

259+10000000000000000.0000000000000000000, +0.499999998670192398661891072794731130

260+100000000000000000.000000000000000000, +0.499999999579477912996639991935446092

261+1000000000000000000.00000000000000000, +0.499999999867019239866189107352612551

262+10000000000000000000.0000000000000000, +0.499999999957947791299663999195857459

263+100000000000000000000.000000000000000, +0.499999999986701923986618910735334373

264+1000000000000000000000.00000000000000, +0.499999999995794779129966399919588057

265+10000000000000000000000.0000000000000, +0.499999999998670192398661891073533500

266+100000000000000000000000.000000000000, +0.499999999999579477912996639991958825

267+1000000000000000000000000.00000000000, +0.499999999999867019239866189107353336

268+10000000000000000000000000.0000000000, +0.499999999999957947791299663999195868

269+100000000000000000000000000.000000000, +0.499999999999986701923986618910735343

270+1000000000000000000000000000.00000000, +0.499999999999995794779129966399919601

271+10000000000000000000000000000.0000000, +0.499999999999998670192398661891073510

272+100000000000000000000000000000.000000, +0.499999999999999579477912996639991955

273+1000000000000000000000000000000.00000, +0.499999999999999867019239866189107361

274+10000000000000000000000000000000.0000, +0.499999999999999957947791299663999210

275+100000000000000000000000000000000.000, +0.499999999999999986701923986618910726

276+1000000000000000000000000000000000.00, +0.499999999999999995794779129966399940

277+10000000000000000000000000000000000.0, +0.499999999999999998670192398661891058

278+100000000000000000000000000000000000., +0.499999999999999999579477912996639970

279+0.100000000000000000000000000000000000E+37, +0.499999999999999999867019239866189106

280+0.100000000000000000000000000000000000E+38, +0.499999999999999999957947791299664011

281+0.100000000000000000000000000000000000E+39, +0.499999999999999999986701923986618906

282+0.100000000000000000000000000000000000E+40, +0.499999999999999999995794779129966411

283+0.100000000000000000000000000000000000E+41, +0.499999999999999999998670192398661910

284+0.100000000000000000000000000000000000E+42, +0.499999999999999999999579477912996651

285+0.100000000000000000000000000000000000E+43, +0.499999999999999999999867019239866210

286+0.100000000000000000000000000000000000E+44, +0.499999999999999999999957947791299655

287+0.100000000000000000000000000000000000E+45, +0.499999999999999999999986701923986635

288+0.100000000000000000000000000000000000E+46, +0.499999999999999999999995794779129951

289+0.100000000000000000000000000000000000E+47, +0.499999999999999999999998670192398639

290+0.100000000000000000000000000000000000E+48, +0.499999999999999999999999579477913005

291+0.100000000000000000000000000000000000E+49, +0.499999999999999999999999867019239883

292+0.999999999999999999999999999999999944E+49, +0.499999999999999999999999957947791276

293+0.100000000000000000000000000000000008E+51, +0.499999999999999999999999986701923998

294+0.100000000000000000000000000000000001E+52, +0.499999999999999999999999995794779152

295+0.100000000000000000000000000000000004E+53, +0.499999999999999999999999998670192414

296+0.100000000000000000000000000000000008E+54, +0.499999999999999999999999999579477915

297+0.100000000000000000000000000000000004E+55, +0.499999999999999999999999999867019256

298+0.100000000000000000000000000000000004E+56, +0.499999999999999999999999999957947801

299+0.999999999999999999999999999999999950E+56, +0.499999999999999999999999999986701935

300+0.100000000000000000000000000000000003E+58, +0.499999999999999999999999999995794780

301+0.100000000000000000000000000000000006E+59, +0.499999999999999999999999999998670194

302+0.100000000000000000000000000000000003E+60, +0.499999999999999999999999999999579473

303+0.100000000000000000000000000000000003E+61, +0.499999999999999999999999999999867015

304+0.100000000000000000000000000000000000E+62, +0.499999999999999999999999999999957967

305+0.100000000000000000000000000000000003E+63, +0.499999999999999999999999999999986711

306+0.100000000000000000000000000000000003E+64, +0.499999999999999999999999999999995811

307+0.999999999999999999999999999999999962E+64, +0.499999999999999999999999999999998652

308+0.100000000000000000000000000000000001E+66, +0.499999999999999999999999999999999567

309+0.999999999999999999999999999999999932E+66, +0.499999999999999999999999999999999856

310

311

Postprocessing of the example output ⛓
1#!/usr/bin/env python

2

3import matplotlib.pyplot as plt

4import pandas as pd

5import numpy as np

6import glob

7import sys

8

9fontsize = 17

10

11kind = "RK"

12label = [ r"shape: $\kappa = 1.0$"

13 , r"shape: $\kappa = 2.5$"

14 , r"shape: $\kappa = 5.0$"

15 ]

16

17pattern = "*." + kind + ".txt"

18fileList = glob.glob(pattern)

19if len(fileList) == 1:

20

21 df = pd.read_csv(fileList[0], delimiter = " ")

22

23 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)

24 ax = plt.subplot()

25

26 for i in range(1,len(df.values[0,:]+1)):

27

28 plt.plot( df.values[:, 0]

29 , df.values[:,i]

30 , linewidth = 2

31 )

32

33 plt.xticks(fontsize = fontsize - 2)

34 plt.yticks(fontsize = fontsize - 2)

35 ax.set_xlabel("x", fontsize = fontsize)

36 ax.set_ylabel("Regularized Upper\nIncomplete Gamma Function", fontsize = fontsize)

37

38 plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")

39 ax.tick_params(axis = "y", which = "minor")

40 ax.tick_params(axis = "x", which = "minor")

41

42 ax.legend ( label

43 , fontsize = fontsize

44 #, loc = "center left"

45 #, bbox_to_anchor = (1, 0.5)

46 )

47

48 plt.savefig(fileList[0].replace(".txt",".png"))

49

50else:

51

52 sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:: test_pm_mathGammaGil

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Fatemeh Bagheri, Monday 12:36 pm, August 16, 2021, Dallas TX

Definition at line 273 of file pm_mathGammaGil.F90.

The documentation for this interface was generated from the following file:

src/fortran/main/pm_mathGammaGil.F90