pm_distGamma::setGammaRand Interface Reference

Return a scalar or array of arbitrary rank of Gamma-distributed random values with the specified shape and scale parameters \((\kappa, \sigma)\) of the Gamma distribution corresponding to the procedure arguments (kappa, sigma). More...

Detailed Description

Return a scalar or array of arbitrary rank of Gamma-distributed random values with the specified shape and scale parameters \((\kappa, \sigma)\) of the Gamma distribution corresponding to the procedure arguments (kappa, sigma).

See the documentation of pm_distGamma for more information on the Probability Density Function (PDF) of the Gamma distribution.

Parameters

[in,out]	rng	: The input/output scalar that can be an object of, type rngf_type, implying the use of intrinsic Fortran uniform RNG for Gamma RNG. type xoshiro256ssw_type, implying the use of xoshiro256** uniform RNG for Gamma RNG. (optional, default = rngf_type, implying the use of the intrinsic Fortran URNG.)
[out]	rand	: The output scalar or array of rank 1, or array of arbitrary rank if the rng argument is missing or set to rngf_type, or of, type real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128). On output, it contains Gamma-distributed random value(s).
[in]	kappa	: The input scalar (or array of the same shape as other array-like arguments) of the same type and kind as rand, representing the shape parameter of the Gamma distribution.
[in]	sigma	: The input scalar (or array of the same shape as other array-like arguments) of the same type and kind as rand, representing the scale parameter of the Gamma distribution.

Possible calling interfaces ⛓

use pm_distGamma, only: setGammaRand
 
call setGammaRand(rand, kappa, sigma)
call setGammaRand(rand(..), kappa, sigma)
call setGammaRand(rng, rand, kappa, sigma)
call setGammaRand(rng, rand(:), kappa, sigma)

Warning

The condition 0 < kappa must hold for the corresponding input arguments.
The condition 0 < sigma must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

Remarks

The procedures under discussion are impure.

The procedures under discussion are elemental.

The procedures under discussion are recursive.

Note

For repeated Gamma RNG with fixed kappa, it is best to pass a vector of rand to be filled with random numbers rather than calling the procedures with scalar rand argument repeatedly.
In addition to avoiding procedure call overhead, vectorized RGN in this particular case also avoids an unnecessary division and square-root operation.

See also

getGammaLogPDF
setGammaLogPDF
getGammaCDF
setGammaCDF

Example usage ⛓

program example
 
    use pm_kind, only: SK, IK
    use pm_kind, only: RKG => RKS ! all real kinds are supported.
    use pm_distGamma, only: setGammaRand
    use pm_arraySpace, only: setLinSpace
    use pm_arraySpace, only: setLogSpace
    use pm_io, only: display_type
 
    implicit none
 
    integer(IK), parameter  :: NP = 1000_IK
    real(RKG), dimension(NP) :: Kappa, Sigma, rand
 
    type(display_type) :: disp
    disp = display_type(file = "main.out.F90")
 
    call setLogSpace(Kappa, logx1 = log(0.1_RKG), logx2 = log(10._RKG))
    call setLogSpace(Sigma, logx1 = log(0.1_RKG), logx2 = log(10._RKG))
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("! Generate random numbers from the Gamma distribution.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("! Gamma random value given integer shape and real inverse rate parameters.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("Kappa(1)")
    call disp%show( Kappa(1) )
    call disp%show("Sigma(1)")
    call disp%show( Sigma(1) )
    call disp%show("call setGammaRand(rand(1:2), 1._RKG, sigma = Sigma(1))")
                    call setGammaRand(rand(1:2), 1._RKG, sigma = Sigma(1))
    call disp%show("rand(1)")
    call disp%show( rand(1) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("! Gamma random value given real shape and real inverse rate parameters.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("Kappa(1)")
    call disp%show( Kappa(1) )
    call disp%show("Sigma(1)")
    call disp%show( Sigma(1) )
    call disp%show("call setGammaRand(rand(1:2), Kappa(1), sigma = Sigma(1))")
                    call setGammaRand(rand(1:2), Kappa(1), sigma = Sigma(1))
    call disp%show("rand(1)")
    call disp%show( rand(1) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("! Gamma random numbers with a fixed set of parameters.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("Kappa(1:NP:NP/3)")
    call disp%show( Kappa(1:NP:NP/3) )
    call disp%show("Sigma(1:NP:NP/3)")
    call disp%show( Sigma(1:NP:NP/3) )
    call disp%show("call setGammaRand(rand(1:NP:NP/3), Kappa(1), sigma = Sigma(1))")
                    call setGammaRand(rand(1:NP:NP/3), Kappa(1), sigma = Sigma(1))
    call disp%show("rand(1:NP:NP/3)")
    call disp%show( rand(1:NP:NP/3) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("! Gamma random numbers for a range of parameters.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    call disp%skip()
    call disp%show("Kappa(1:NP:NP/3)")
    call disp%show( Kappa(1:NP:NP/3) )
    call disp%show("Sigma(1:NP:NP/3)")
    call disp%show( Sigma(1:NP:NP/3) )
    call disp%show("call setGammaRand(rand(1:NP:NP/3), Kappa(1:NP:NP/3), sigma = Sigma(1:NP:NP/3))")
                    call setGammaRand(rand(1:NP:NP/3), Kappa(1:NP:NP/3), sigma = Sigma(1:NP:NP/3))
    call disp%show("rand(1:NP:NP/3)")
    call disp%show( rand(1:NP:NP/3) )
    call disp%skip()
 
    call disp%skip()
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%show("! Test the mean of a random sample against the analytic answer.")
    call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
    call disp%skip()
 
    block
        use pm_sampleMean, only: getMean
        use pm_distExp, only: getExpRand
        real(RKG) :: kappa, omega, sigma, mean
        integer(IK) :: itry
        do itry = 1, 30
            call disp%skip()
            call disp%show("kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)")
                            kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
            call disp%show("[kappa, sigma]")
            call disp%show( [kappa, sigma] )
            call disp%show("call setGammaRand(rand, kappa, sigma)")
                            call setGammaRand(rand, kappa, sigma)
            call disp%show("mean = kappa * sigma")
                            mean = kappa * sigma
            call disp%show("[getMean(rand), mean]")
            call disp%show( [getMean(rand), mean] )
            call disp%skip()
        end do
    end block
 
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    ! Output an example rand array for visualization.
    !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
    block
        use pm_io, only: getErrTableWrite
        real(RKG):: rand(5000, 3)
        call setGammaRand(rand(:, 1), +0.8_RKG, sigma = 2._RKG)
        call setGammaRand(rand(:, 2), +1.0_RKG, sigma = 2._RKG)
        call setGammaRand(rand(:, 3), +5.0_RKG, sigma = 2._RKG)
        if (0 /= getErrTableWrite(SK_"setGammaRand.RK.txt", rand)) error stop "Table writing failed."
    end block
 
end program example

Example Unix compile command via Intel ifort compiler ⛓

#!/usr/bin/env sh
rm main.exe
ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓

del main.exe
set PATH=..\..\..\lib;%PATH%
ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓

#!/usr/bin/env sh
rm main.exe
gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
./main.exe

Example output ⛓

 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Generate random numbers from the Gamma distribution.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Gamma random value given integer shape and real inverse rate parameters.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
Kappa(1)
+0.999999940E-1
Sigma(1)
+0.999999940E-1
call setGammaRand(rand(1:2), 1._RKG, sigma = Sigma(1))
rand(1)
+0.598768368E-1
 
 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Gamma random value given real shape and real inverse rate parameters.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
Kappa(1)
+0.999999940E-1
Sigma(1)
+0.999999940E-1
call setGammaRand(rand(1:2), Kappa(1), sigma = Sigma(1))
rand(1)
+0.195523188
 
 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Gamma random numbers with a fixed set of parameters.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
Kappa(1:NP:NP/3)
+0.999999940E-1, +0.464158833, +2.15443444, +10.0000010
Sigma(1:NP:NP/3)
+0.999999940E-1, +0.464158833, +2.15443444, +10.0000010
call setGammaRand(rand(1:NP:NP/3), Kappa(1), sigma = Sigma(1))
rand(1:NP:NP/3)
+0.326829441E-1, +0.922724523E-18, +0.405257754E-2, +0.647063134E-4
 
 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Gamma random numbers for a range of parameters.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
Kappa(1:NP:NP/3)
+0.999999940E-1, +0.464158833, +2.15443444, +10.0000010
Sigma(1:NP:NP/3)
+0.999999940E-1, +0.464158833, +2.15443444, +10.0000010
call setGammaRand(rand(1:NP:NP/3), Kappa(1:NP:NP/3), sigma = Sigma(1:NP:NP/3))
rand(1:NP:NP/3)
+0.125135131E-14, +0.188318808E-1, +5.77179337, +106.766060
 
 
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
! Test the mean of a random sample against the analytic answer.
!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.718482077, +0.307035238
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.211707696, +0.220599309
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.897499144, +0.620168820E-1
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.527538955E-1, +0.556600988E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.482126296, +0.244318679
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.124512605, +0.117792457
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+1.84421015, +0.326677233
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.583081722, +0.602461457
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.916445196, +0.540956736
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.486813426, +0.495757192
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+2.16448259, +0.974990055E-1
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.202412486, +0.211034894
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.629441798, +0.850616097
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.539749265, +0.535413325
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.766554624E-1, +0.374298632
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.279017799E-1, +0.286920350E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+1.73022115, +0.350722969
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.604909360, +0.606828272
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.308323413, +0.354203403
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.107543424, +0.109209202
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.782472849, +4.04998589
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+3.08144379, +3.16900396
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.497640431, +1.95383561
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.875140965, +0.972307622
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.453534685E-1, +0.373548746
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.191997308E-1, +0.169417318E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+1.24157143, +0.211577863
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.260753363, +0.262689024
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.221977681, +0.131277546
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.302501600E-1, +0.291406848E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.945052147, +3.31201911
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+3.11428642, +3.13003087
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.135524452, +0.732155219E-1
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.909386389E-2, +0.992249325E-2
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+2.04230833, +1.15492058
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+2.41681290, +2.35870385
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.888535023, +4.35371685
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+4.00702858, +3.86842990
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.551930219E-1, +0.731519401
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.306411926E-1, +0.403747670E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.211753607, +0.122067027
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.240774006E-1, +0.258481335E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.299967043E-1, +0.985675812
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.253551845E-1, +0.295670256E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.116013601, +1.93261623
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.230711997, +0.224209771
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.433227062, +0.540476926E-1
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.239297170E-1, +0.234149229E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.512578189, +3.60357952
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+1.96265066, +1.84711623
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+1.95186138, +1.22501266
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+2.37409377, +2.39105487
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+3.34607100, +1.55056524
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+5.23951626, +5.18830156
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.355441153, +0.329112560E-1
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.113170194E-1, +0.116980150E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+1.45416820, +0.552167036E-1
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+0.790459737E-1, +0.802943781E-1
 
 
kappa = getExpRand(1._RKG); sigma = getExpRand(1._RKG)
[kappa, sigma]
+0.425744683, +2.47353053
call setGammaRand(rand, kappa, sigma)
mean = kappa * sigma
[getMean(rand), mean]
+1.10324228, +1.05309248
 
 

Postprocessing of the example output ⛓

#!/usr/bin/env python
 
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import glob
import sys
 
linewidth = 2
fontsize = 17
 
marker ={ "CK" : "-"
        , "IK" : "."
        , "RK" : "-"
        }
xlab =  { "CK" : "Gamma Random Value ( real/imaginary components )"
        , "IK" : "Gamma Random Value ( integer-valued )"
        , "RK" : "Gamma Random Value ( real-valued )"
        }
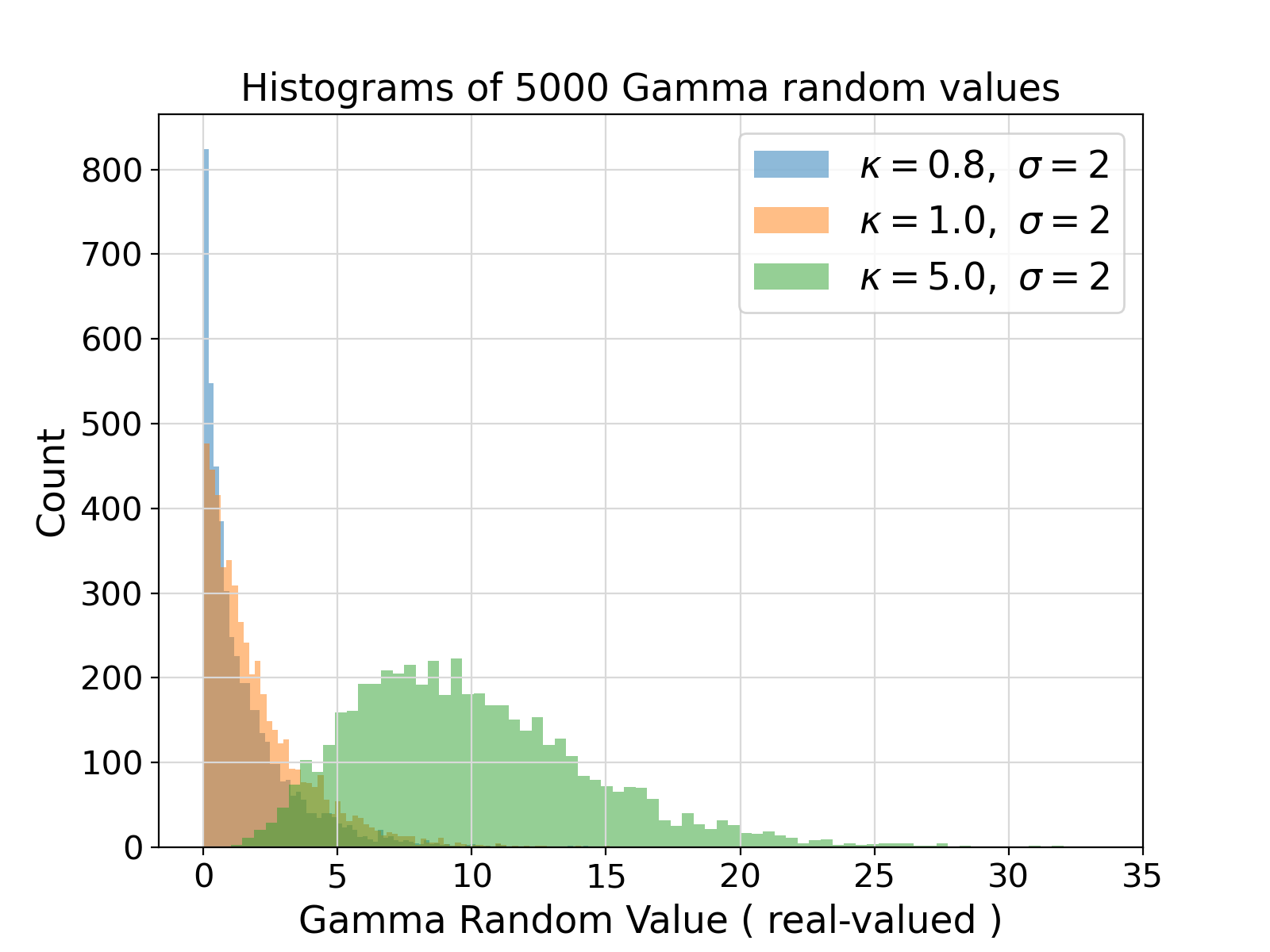
legends =   [ r"$\kappa = 0.8,~\sigma = 2$"
            , r"$\kappa = 1.0,~\sigma = 2$"
            , r"$\kappa = 5.0,~\sigma = 2$"
            ]
 
for kind in ["IK", "CK", "RK"]:
 
    pattern = "*." + kind + ".txt"
    fileList = glob.glob(pattern)
    if len(fileList) == 1:
 
        df = pd.read_csv(fileList[0], delimiter = ",", header = None)
 
        fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
        ax = plt.subplot()
 
        for j in range(len(df.values[0,:])):
            if kind == "CK":
                plt.hist( df.values[:,j]
                        , histtype = "stepfilled"
                        , alpha = 0.5
                        , bins = 75
                        )
            else:
                plt.hist( df.values[:,j]
                        , histtype = "stepfilled"
                        , alpha = 0.5
                        , bins = 75
                        )
                ax.legend   ( legends
                            , fontsize = fontsize
                            )
        plt.xticks(fontsize = fontsize - 2)
        plt.yticks(fontsize = fontsize - 2)
        ax.set_xlabel(xlab[kind], fontsize = 17)
        ax.set_ylabel("Count", fontsize = 17)
        ax.set_title("Histograms of {} Gamma random values".format(len(df.values[:, 0])), fontsize = 17)
 
        plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
        ax.tick_params(axis = "y", which = "minor")
        ax.tick_params(axis = "x", which = "minor")
 
        plt.savefig(fileList[0].replace(".txt",".png"))
 
    elif len(fileList) > 1:
 
        sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:

test_pm_distGamma

Final Remarks ⛓

---

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
   
2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
   

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright

Computational Data Science Lab

Author:

Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan

Definition at line 1193 of file pm_distGamma.F90.

---

The documentation for this interface was generated from the following file:

• src/fortran/main/pm_distGamma.F90