
|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |

|
ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation. |
This module contains abstract and concrete derived types that are required for compile-time resolution of procedures within the generic interfaces of the ParaMonte library for Linear Algebra operations.
Such procedures frequently need to work with different packaging of Symmetric/Hermitian/Band or other special types of their input matrix arguments.
More...
Data Types | |
| interface | isMatPack |
Generate and return .true. if and only if a desired matrix with the specified input shape is of the specified input packing pack.More... | |
| type | lcpack_type |
| This is a concrete derived type whose instances are exclusively used to signify Linear Contiguous Packing format of a subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type | ldpack_type |
| This is a concrete derived type whose instances are exclusively used to signify Linear Sparse (or Standard) Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type | lfpack_type |
| This is a concrete derived type whose instances are exclusively used to signify Linear Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type | package_type |
This is an abstract derived type for constructing concrete derived types to distinguish various procedure signatures that require different forms of matrix packing (triangular, Band, ...).More... | |
| type | rcpack_type |
| This is a concrete derived type whose instances are exclusively used to signify Rectangular Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type | rdpack_type |
| This is a concrete derived type whose instances are exclusively used to signify Rectangular Sparse (or Standard) Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type | rfpack_type |
| This is a concrete derived type whose instances are exclusively used to signify Rectangular Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
Variables | |
| character(*, SK), parameter | MODULE_NAME = "@pm_matrixPack" |
| type(rdpack_type), parameter | rdpack = rdpack_type() |
| This is an object instance of class rdpack_type that is exclusively used to signify Rectangular Sparse (or Standard) Packing format of a given (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type(lfpack_type), parameter | lfpack = lfpack_type() |
| This is an object instance of class lfpack_type that is exclusively used to signify Linear Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
| type(rfpack_type), parameter | rfpack = rfpack_type() |
| This is an object instance of class rfpack_type that is exclusively used to signify Rectangular Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library. More... | |
This module contains abstract and concrete derived types that are required for compile-time resolution of procedures within the generic interfaces of the ParaMonte library for Linear Algebra operations.
Such procedures frequently need to work with different packaging of Symmetric/Hermitian/Band or other special types of their input matrix arguments.
This module follows the conventions of the LAPACK Linear Algebra Fortran software for matrix package schemes.
LAPACK routines use the following matrix package schemes:
\begin{equation} L = \begin{bmatrix} \ell_{1,1} & & & & \\ \ell_{2,1} & \ell_{2,2} & & & \\ \ell_{3,1} & \ell_{3,2} & \ddots & & \\ \vdots & \vdots & \ddots & \ell_{n-1,n-1} & \\ \ell_{n,1} & \ell_{n,2} & \ldots & \ell_{n,n-1} & \ell_{n,n} \end{bmatrix} ~, \end{equation}
translates to the packed (column-major) format,\begin{equation} L_{\mathrm{packed}} = [ \ell_{1,1}, \ell_{2,1}, \ell_{3,1}, \ldots, \ell_{n,1}, \ell_{2,2}, \ell_{3,2}, \ldots, \ell_{n,2}, \ldots, \ell_{n-1,n-1}, \ell_{n,n-1}, \ell_{n,n} ] ~. \end{equation}
In general, the indices (i, j), 1\leq j\leq i \leq n of a full lower-diagonal n\times n matrix translate to packed vector index,\begin{equation} U = \begin{bmatrix} u_{1,1} & u_{1,2} & u_{1,3} & \ldots & u_{1,n} \\ & u_{2,2} & u_{2,3} & \ldots & u_{2,n} \\ & & u_{3,3} & \ddots & \vdots \\ & & & \ddots & u_{n-1,n} \\ & & & & u_{n,n} \end{bmatrix} ~, \end{equation}
translates to the packed (column-major) format,\begin{equation} U_{\mathrm{packed}} = [ u_{1,1}, u_{1,2}, u_{1,2}, u_{1,3}, u_{2,3}, u_{3,3}, \ldots, u_{1,n}, u_{2,n}, u_{3,2}, \ldots, u_{n-1,n}, u_{n,n} ] ~. \end{equation}
In general, the indices (i, j), 1\leq i\leq j \leq n of a full upper-diagonal n\times n matrix translate to the packed vector index,LAPACK_COL_MAJOR) or row major (with the value LAPACK_ROW_MAJOR) matrix layout.uplo in the LAPACK library), which specifies which upper/lower triangle of the matrix is packed in RFP format."U" and "L" respectively.

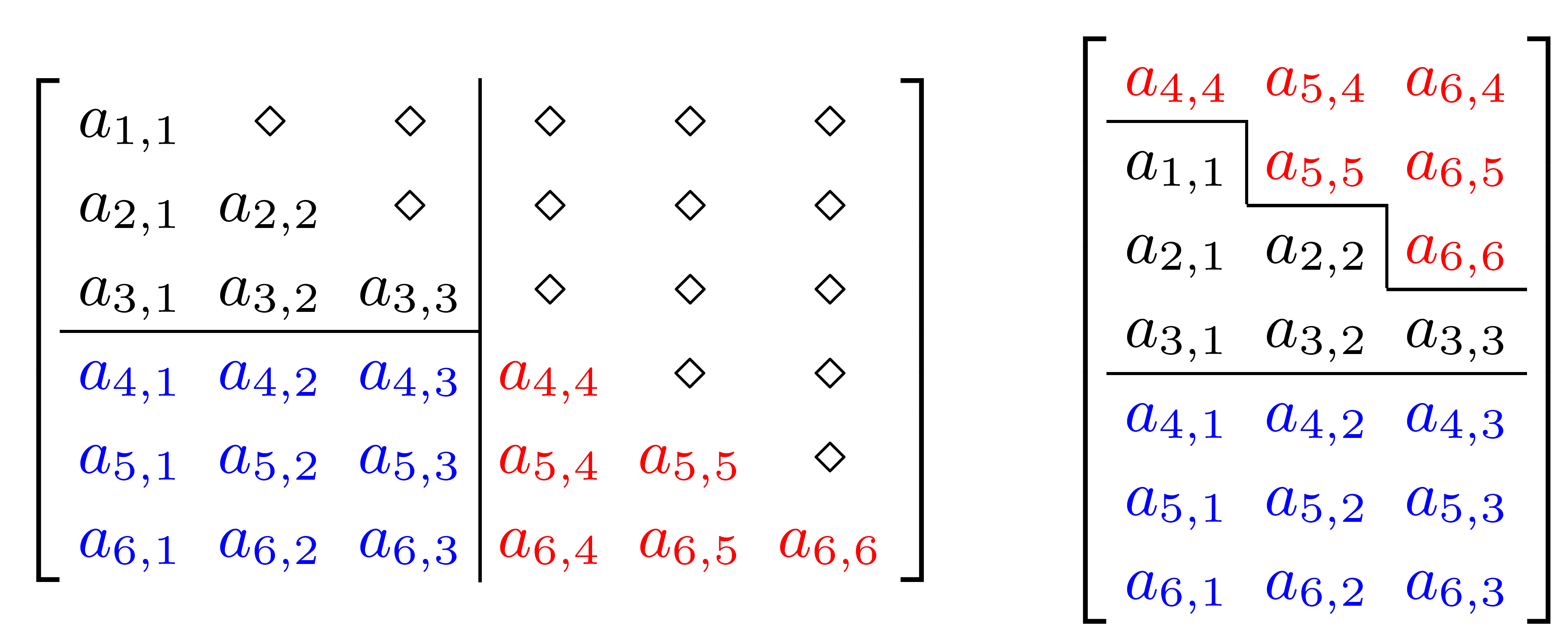

transA or transB in the LAPACK library), which specifies one of the following three transposition operations on the matrix, "N"). "T"). "C"). Rectangular Default (i.e., standard, no specific) packing (RDP or rdpack)
This is the regular matrix package.
An m\times n full matrix A has the form,
\begin{equation} \large \mathbf{A} = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} ~. \end{equation}
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
| type(lfpack_type), parameter pm_matrixPack::lfpack = lfpack_type() |
This is an object instance of class lfpack_type that is exclusively used to signify Linear Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 401 of file pm_matrixPack.F90.
| character(*,SK), parameter pm_matrixPack::MODULE_NAME = "@pm_matrixPack" |
Definition at line 132 of file pm_matrixPack.F90.
| type(rdpack_type), parameter pm_matrixPack::rdpack = rdpack_type() |
This is an object instance of class rdpack_type that is exclusively used to signify Rectangular Sparse (or Standard) Packing format of a given (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 263 of file pm_matrixPack.F90.
| type(rfpack_type), parameter pm_matrixPack::rfpack = rfpack_type() |
This is an object instance of class rfpack_type that is exclusively used to signify Rectangular Full contiguous Packing format of a (triangular) subset of a matrix within an interface of a procedure of the ParaMonte library.
For example usage, see the documentation of the target procedure requiring this object.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
Definition at line 468 of file pm_matrixPack.F90.