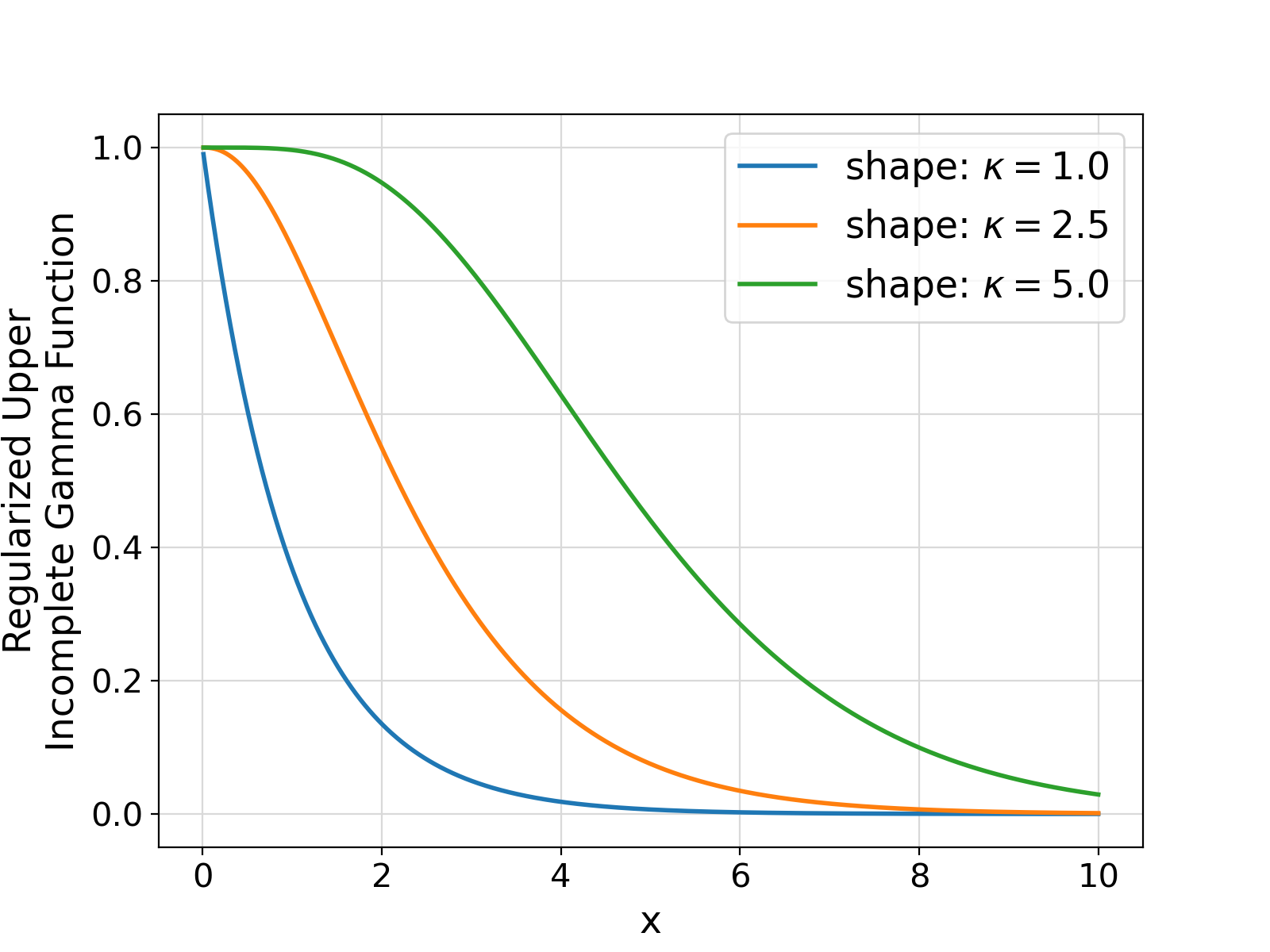
Generate and return the regularized Upper Incomplete Gamma function for the specified shape parameter ( $\kappa$) and lower limit of the integral x. More...

Detailed Description

Generate and return the regularized Upper Incomplete Gamma function for the specified shape parameter ( $\kappa$) and lower limit of the integral x.

The regularized Upper Incomplete Gamma function is defined as,

\begin{equation} \large Q(\kappa, x) = \frac{1}{\Gamma(\kappa)} \int_x^{+\infty}~t^{\kappa-1}{\mathrm e}^{-t} ~ dt ~, \end{equation}

where $(\kappa > 0, x > 0)$ should hold, with $\kappa$ representing the shape parameter of the Gamma function (or distribution) and $x$ representing the lower limit in the integral of the Upper Incomplete Gamma function.
Note that this integral is bounded between zero and one ( $[0,1]$).
The regularized Upper Incomplete Gamma function also represents the complement of the Cumulative Distribution Function (CDF) of the univariate Gamma distribution with the specified shape parameter and standardized x (with the scale parameter of unity).

Parameters

[in]	x	: The input scalar of type `real` of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), representing the lower limit in the integral of the Lower Incomplete Gamma function $P(\kappa,x)$.
[in]	kappa	: The input scalar of the same type and kind as `x`, representing the shape parameter ( $\kappa$) of the Lower Incomplete Gamma function $P(\kappa,x)$.
[in]	tol	: The input scalar of the same type and kind as `x`, representing the relative accuracy in the convergence checking of the Gamma series or its Legendre continued fraction representation. (optional, default is set by setGammaIncUppNR())

Returns: gammaIncUpp : The output scalar of the same type and kind as the output argument x representing the Upper Incomplete Gamma function for the specified kappa and lower limit.
Note that gammaIncUpp is, by definition, always positive.
Note that the procedure will abruptly end the program by calling error stop if the computation of the Incomplete Gamma function fails to converge.

Possible calling interfaces ⛓

: use pm_mathGammaNR, only: getGammaIncUppNR

gammaIncUpp = getGammaIncUppNR(x, kappa, tol = tol)

pm_mathGammaNR::getGammaIncUppNR
Generate and return the regularized Upper Incomplete Gamma function for the specified shape parameter...
Definition: pm_mathGammaNR.F90:326

pm_mathGammaNR
This module contains procedures and generic interfaces for the Lower and Upper Incomplete Gamma funct...
Definition: pm_mathGammaNR.F90:86

Warning: The kappa and x input arguments must be positive real numbers.
Furthermore, tol << 1. must hold, if present as an input argument.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.

Remarks: The procedures under discussion are impure.; The procedures under discussion are elemental.; The procedures under this generic interface solely provide a more convenient method of calling the subroutine equivalents setGammaIncUppNR.
As such they are slower than the corresponding subroutine version.

See also: getGammaIncLowNR
setGammaIncUppNR

Example usage ⛓

: 1program example

2

3 use pm_kind, only: SK

4 use pm_kind, only: IK

5 use pm_kind, only: LK

6 use pm_kind, only: RKS, RKD, RKH

7 use pm_io, only: display_type

8 use pm_mathGammaNR, only: getGammaIncUppNR

9

10 implicit none

11

12 type(display_type) :: disp

13 disp = display_type(file = "main.out.F90")

14

15 call disp%skip()

16 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

17 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

18 call disp%show("! Compute the regularized Upper Incomplete Gamma Function using its series representation.")

19 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

20 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

21 call disp%skip()

22

23 call disp%skip()

24 call disp%show("getGammaIncUppNR(x = 1.5_RKS, kappa = 2._RKS)")

25 call disp%show( getGammaIncUppNR(x = 1.5_RKS, kappa = 2._RKS) )

26 call disp%skip()

27

28 call disp%skip()

29 call disp%show("getGammaIncUppNR(x = 1.5_RKD, kappa = 2._RKD)")

30 call disp%show( getGammaIncUppNR(x = 1.5_RKD, kappa = 2._RKD) )

31 call disp%skip()

32

33 call disp%skip()

34 call disp%show("getGammaIncUppNR(x = 1.5_RKH, kappa = 2._RKH)")

35 call disp%show( getGammaIncUppNR(x = 1.5_RKH, kappa = 2._RKH) )

36 call disp%skip()

37

38 call disp%skip()

39 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

40 call disp%show("! Compute the regularized Upper Incomplete Gamma Function for a vector of points.")

41 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

42 call disp%skip()

43

44 call disp%skip()

45 call disp%show("getGammaIncUppNR(x = 1.5_RKH, kappa = [real(RKH) :: 2, 20, 200])")

46 call disp%show( getGammaIncUppNR(x = 1.5_RKH, kappa = [real(RKH) :: 2, 20, 200]) )

47 call disp%skip()

48

49 call disp%skip()

50 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

51 call disp%show("! Compute the regularized Upper Incomplete Gamma Function for a vector of kappa parameters.")

52 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

53 call disp%skip()

54

55 call disp%skip()

56 call disp%show("getGammaIncUppNR(x = 1._RKS, kappa = [0.1_RKS, 1._RKS, 10._RKS])")

57 call disp%show( getGammaIncUppNR(x = 1._RKS, kappa = [0.1_RKS, 1._RKS, 10._RKS]) )

58 call disp%skip()

59

60 call disp%skip()

61 call disp%show("getGammaIncUppNR(x = 1._RKD, kappa = [0.1_RKD, 1._RKD, 10._RKD])")

62 call disp%show( getGammaIncUppNR(x = 1._RKD, kappa = [0.1_RKD, 1._RKD, 10._RKD]) )

63 call disp%skip()

64

65 call disp%skip()

66 call disp%show("getGammaIncUppNR(x = 1._RKH, kappa = [0.1_RKH, 1._RKH, 10._RKH])")

67 call disp%show( getGammaIncUppNR(x = 1._RKH, kappa = [0.1_RKH, 1._RKH, 10._RKH]) )

68 call disp%skip()

69

70

71 call disp%skip()

72 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

73 call disp%show("! Compute the regularized Upper Incomplete Gamma Function for a vector of points and kappa parameters.")

74 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

75 call disp%skip()

76

77

78 call disp%skip()

79 call disp%show("getGammaIncUppNR(x = [1._RKS, 1._RKS, 1._RKS], kappa = [0.1_RKS, 1._RKS, 10._RKS])")

80 call disp%show( getGammaIncUppNR(x = [1._RKS, 1._RKS, 1._RKS], kappa = [0.1_RKS, 1._RKS, 10._RKS]) )

81 call disp%skip()

82

83 call disp%skip()

84 call disp%show("getGammaIncUppNR(x = [1._RKD, 1._RKD, 1._RKD], kappa = [0.1_RKD, 1._RKD, 10._RKD])")

85 call disp%show( getGammaIncUppNR(x = [1._RKD, 1._RKD, 1._RKD], kappa = [0.1_RKD, 1._RKD, 10._RKD]) )

86 call disp%skip()

87

88 call disp%skip()

89 call disp%show("getGammaIncUppNR(x = [1._RKH, 1._RKH, 1._RKH], kappa = [0.1_RKH, 1._RKH, 10._RKH])")

90 call disp%show( getGammaIncUppNR(x = [1._RKH, 1._RKH, 1._RKH], kappa = [0.1_RKH, 1._RKH, 10._RKH]) )

91 call disp%skip()

92

93

94 call disp%skip()

95 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

96 call disp%show("! Compute the regularized Upper Incomplete Gamma Function for a fixed point and kappa parameter, but with different accuracies.")

97 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

98 call disp%skip()

99

100 call disp%skip()

101 call disp%show("getGammaIncUppNR(x = 1._RKH, kappa = 2._RKH, tol = [1.e-8_RKH, 1.e-16_RKH, 1.e-32_RKH])")

102 call disp%show( getGammaIncUppNR(x = 1._RKH, kappa = 2._RKH, tol = [1.e-8_RKH, 1.e-16_RKH, 1.e-32_RKH]) )

103 call disp%skip()

104

105

106 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

107 ! Output an example array of the regularized Upper Incomplete Gamma function for visualization.

108 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

109

110 block

111

112 use pm_arraySpace, only: setLinSpace

113 integer(IK) , parameter :: NP = 1000_IK

114 real(RKS) :: x_RKS(NP)

115 integer :: fileUnit, i

116

117 call setLinSpace(x_RKS, 0._RKS, 10._RKS)

118 open(newunit = fileUnit, file = "getGammaIncUppNR.RK.txt")

119 do i = 1, NP

120 write(fileUnit, "(*(g0,:,' '))") x_RKS(i), getGammaIncUppNR(x_RKS(i), kappa = [1.0_RKS, 2.5_RKS, 5.0_RKS])

121 end do

122 close(fileUnit)

123

124 end block

125

126end program example

pm_arraySpace::setLinSpace
Return the linSpace output argument with size(linSpace) elements of evenly-spaced values over the int...
Definition: pm_arraySpace.F90:324

pm_io::show
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11726

pm_io::skip
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11508

pm_arraySpace
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
Definition: pm_arraySpace.F90:33

pm_io
This module contains classes and procedures for input/output (IO) or generic display operations on st...
Definition: pm_io.F90:252

pm_io::disp
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
Definition: pm_io.F90:11393

pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268

pm_kind::LK
integer, parameter LK
The default logical kind in the ParaMonte library: kind(.true.) in Fortran, kind(....
Definition: pm_kind.F90:541

pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540

pm_kind::RKD
integer, parameter RKD
The double precision real kind in Fortran mode. On most platforms, this is an 64-bit real kind.
Definition: pm_kind.F90:568

pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539

pm_kind::RKH
integer, parameter RKH
The scalar integer constant of intrinsic default kind, representing the highest-precision real kind t...
Definition: pm_kind.F90:858

pm_kind::RKS
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Definition: pm_kind.F90:567

pm_io::display_type
Generate and return an object of type display_type.
Definition: pm_io.F90:10282

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe

2set PATH=..\..\..\lib;%PATH%

3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe

4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example output ⛓
1

2!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

3!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

4! Compute the regularized Upper Incomplete Gamma Function using its series representation.

5!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

6!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

7

8

9getGammaIncUppNR(x = 1.5_RKS, kappa = 2._RKS)

10+0.557825506

11

12

13getGammaIncUppNR(x = 1.5_RKD, kappa = 2._RKD)

14+0.55782540037107453

15

16

17getGammaIncUppNR(x = 1.5_RKH, kappa = 2._RKH)

18+0.557825400371074572333201176910031393

19

20

21!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

22! Compute the regularized Upper Incomplete Gamma Function for a vector of points.

23!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

24

25

26getGammaIncUppNR(x = 1.5_RKH, kappa = [real(RKH) :: 2, 20, 200])

27+0.557825400371074572333201176910031393, +0.999999999999999671656580338635575848, +1.00000000000000000000000000000000000

28

29

30!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

31! Compute the regularized Upper Incomplete Gamma Function for a vector of kappa parameters.

32!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

33

34

35getGammaIncUppNR(x = 1._RKS, kappa = [0.1_RKS, 1._RKS, 10._RKS])

36+0.241275430E-1, +0.367879391, +0.999999881

37

38

39getGammaIncUppNR(x = 1._RKD, kappa = [0.1_RKD, 1._RKD, 10._RKD])

40+0.24127343726327521E-1, +0.36787944117144233, +0.99999988857452171

41

42

43getGammaIncUppNR(x = 1._RKH, kappa = [0.1_RKH, 1._RKH, 10._RKH])

44+0.241273437263277773829694356333550201E-1, +0.367879441171442321595523770161460873, +0.999999888574521661279322646949312805

45

46

47!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

48! Compute the regularized Upper Incomplete Gamma Function for a vector of points and kappa parameters.

49!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

50

51

52getGammaIncUppNR(x = [1._RKS, 1._RKS, 1._RKS], kappa = [0.1_RKS, 1._RKS, 10._RKS])

53+0.241275430E-1, +0.367879391, +0.999999881

54

55

56getGammaIncUppNR(x = [1._RKD, 1._RKD, 1._RKD], kappa = [0.1_RKD, 1._RKD, 10._RKD])

57+0.24127343726327521E-1, +0.36787944117144233, +0.99999988857452171

58

59

60getGammaIncUppNR(x = [1._RKH, 1._RKH, 1._RKH], kappa = [0.1_RKH, 1._RKH, 10._RKH])

61+0.241273437263277773829694356333550201E-1, +0.367879441171442321595523770161460873, +0.999999888574521661279322646949312805

62

63

64!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

65! Compute the regularized Upper Incomplete Gamma Function for a fixed point and kappa parameter, but with different accuracies.

66!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

67

68

69getGammaIncUppNR(x = 1._RKH, kappa = 2._RKH, tol = [1.e-8_RKH, 1.e-16_RKH, 1.e-32_RKH])

70+0.735758882406482416462388959316297467, +0.735758882342884643349800300430248054, +0.735758882342884643191047540322921745

71

72

Postprocessing of the example output ⛓
1#!/usr/bin/env python

2

3import matplotlib.pyplot as plt

4import pandas as pd

5import numpy as np

6import glob

7import sys

8

9fontsize = 17

10

11kind = "RK"

12label = [ r"shape: $\kappa = 1.0$"

13 , r"shape: $\kappa = 2.5$"

14 , r"shape: $\kappa = 5.0$"

15 ]

16

17pattern = "*." + kind + ".txt"

18fileList = glob.glob(pattern)

19if len(fileList) == 1:

20

21 df = pd.read_csv(fileList[0], delimiter = " ")

22

23 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)

24 ax = plt.subplot()

25

26 for i in range(1,len(df.values[0,:]+1)):

27

28 plt.plot( df.values[:, 0]

29 , df.values[:,i]

30 , linewidth = 2

31 )

32

33 plt.xticks(fontsize = fontsize - 2)

34 plt.yticks(fontsize = fontsize - 2)

35 ax.set_xlabel("x", fontsize = fontsize)

36 ax.set_ylabel("Regularized Upper\nIncomplete Gamma Function", fontsize = fontsize)

37

38 plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")

39 ax.tick_params(axis = "y", which = "minor")

40 ax.tick_params(axis = "x", which = "minor")

41

42 ax.legend ( label

43 , fontsize = fontsize

44 #, loc = "center left"

45 #, bbox_to_anchor = (1, 0.5)

46 )

47

48 plt.savefig(fileList[0].replace(".txt",".png"))

49

50else:

51

52 sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:: test_pm_mathGammaNR

Remarks: See Numerical Recipes by Press et al. 1992 for further details of the Incomplete Gamma function.

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Fatemeh Bagheri, Monday 12:36 pm, August 16, 2021, Dallas TX

Definition at line 326 of file pm_mathGammaNR.F90.

The documentation for this interface was generated from the following file:

src/fortran/main/pm_mathGammaNR.F90