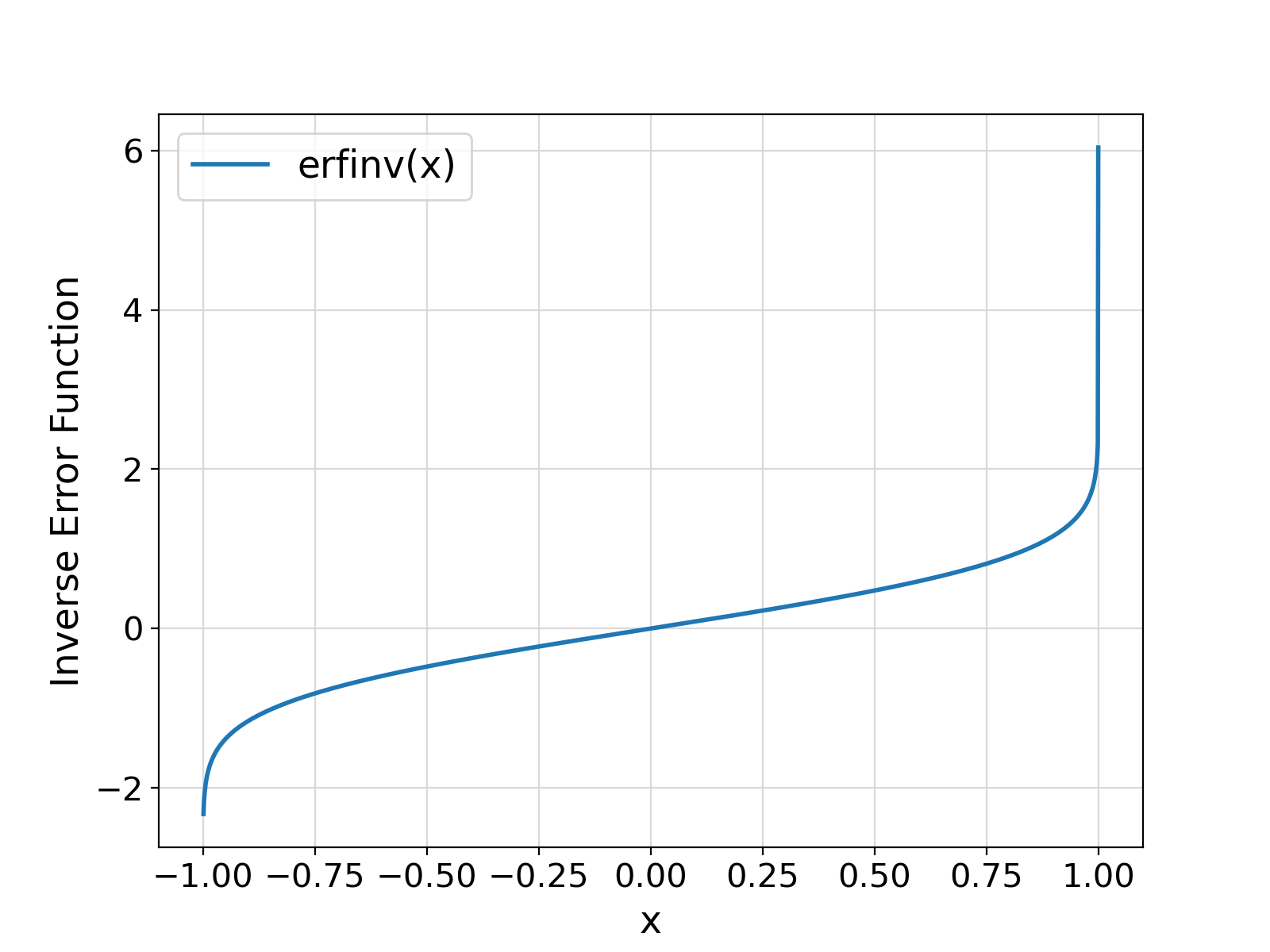
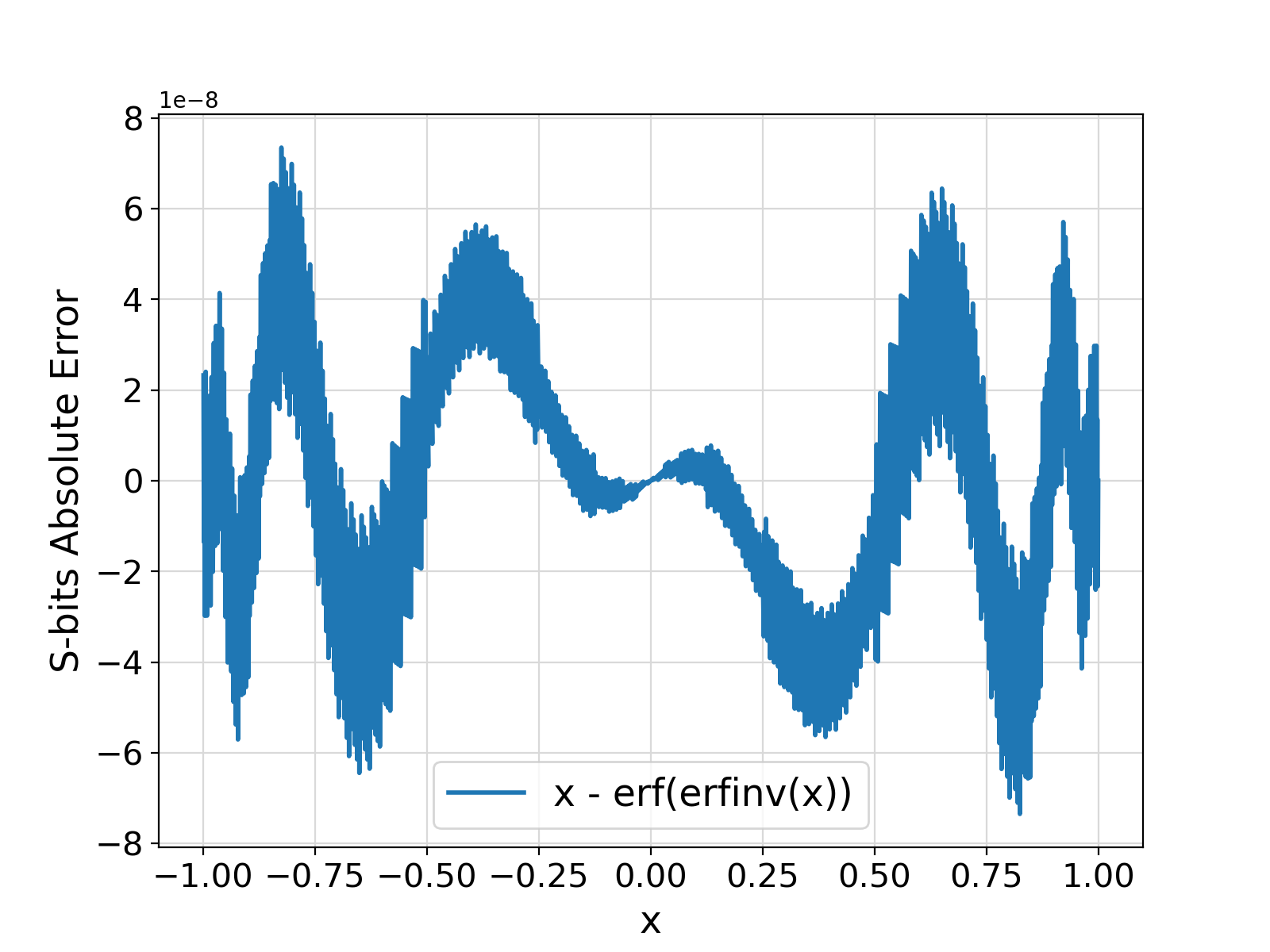
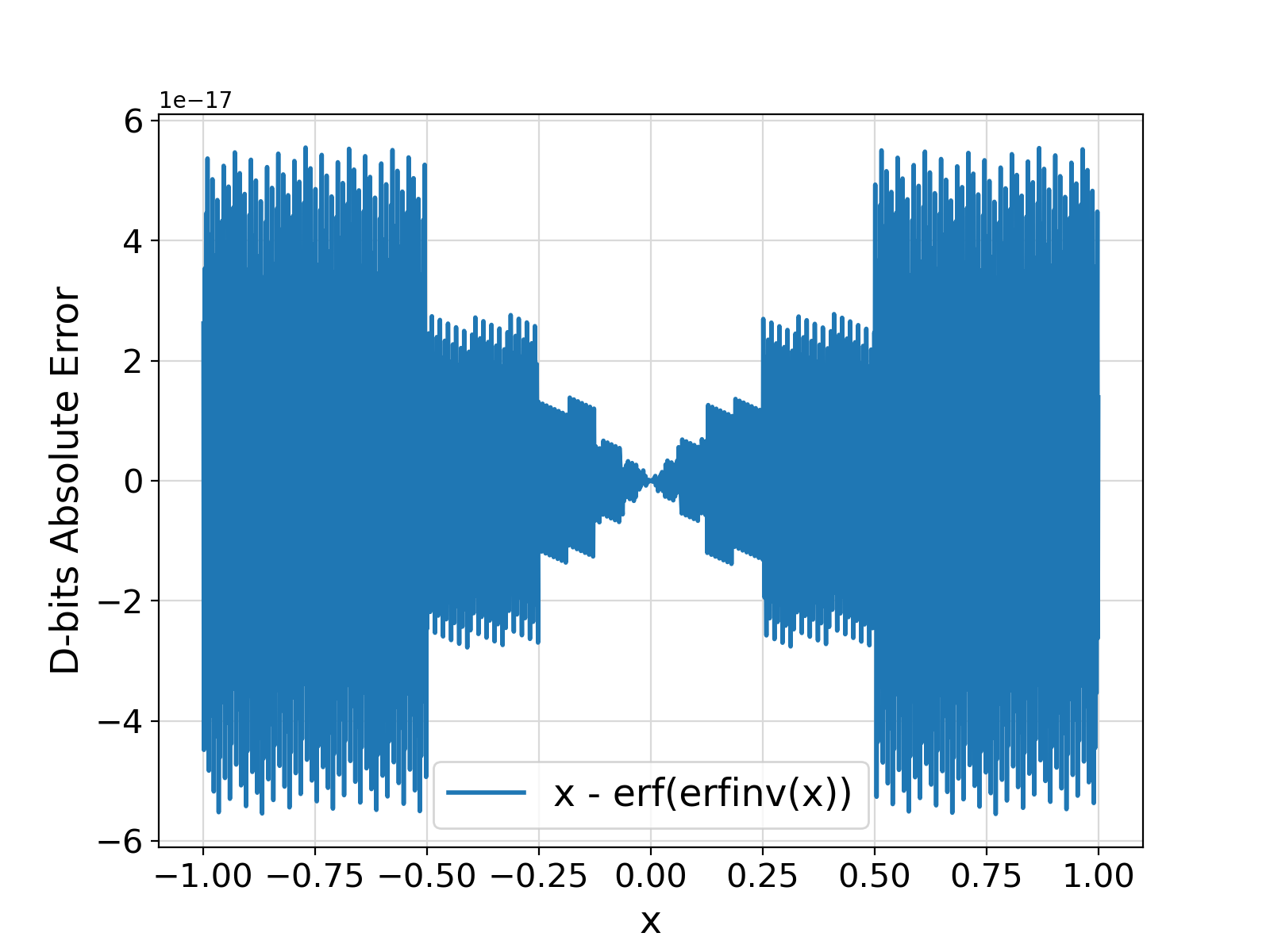
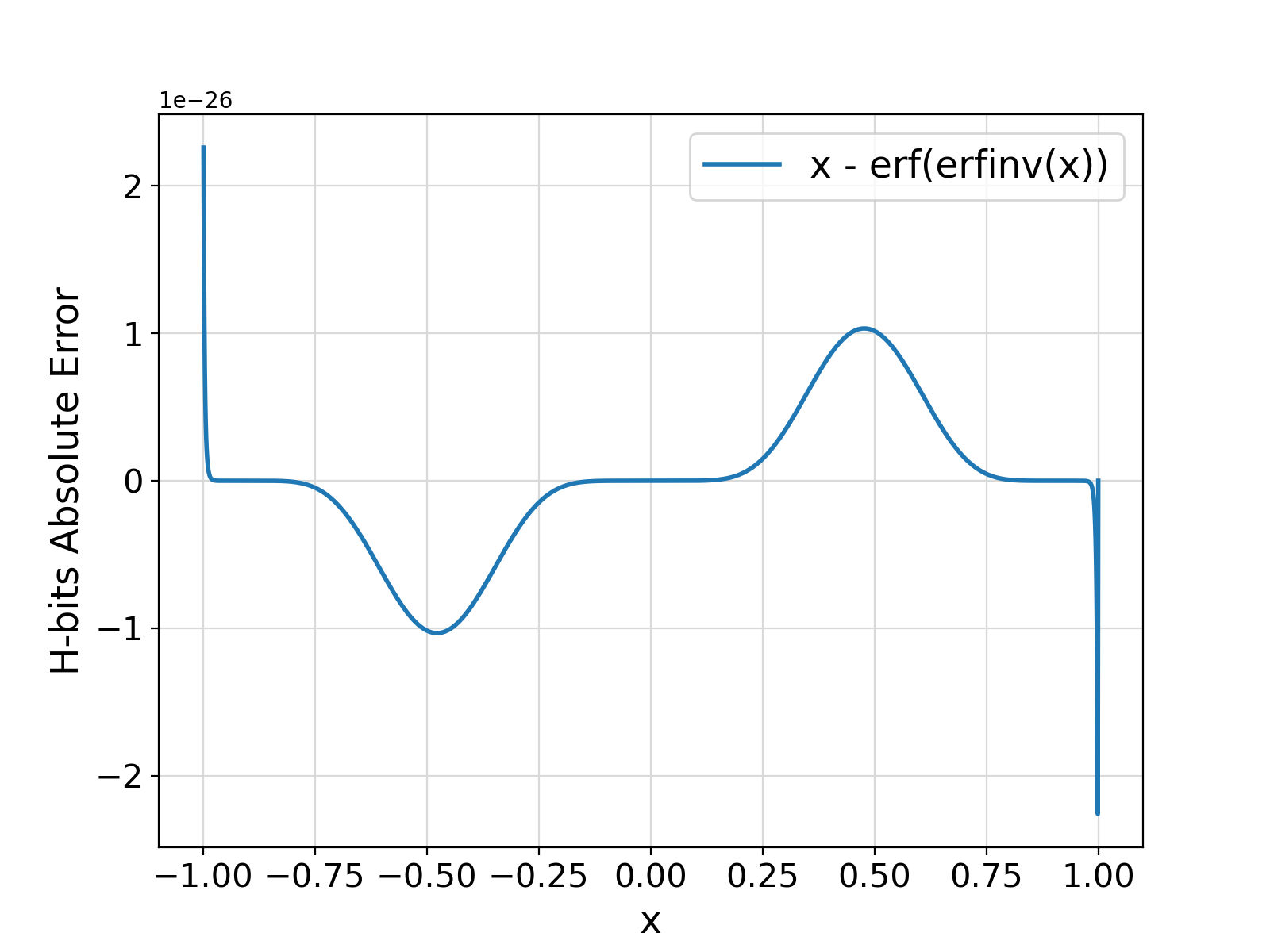
Return the Inverse Error Function \ms{erf}^{-1}(x) for an input real value in range (-1, +1) as defined in the details section of pm_mathErf.
The complementary inverse error function \ms{erfc}^{-1}(y), y\in(0, 2) can be readily computed as call setErfInv(1 - y).
See the documentation of pm_mathErf for more information.
- Parameters
-
| [in] | erfinv | : The output scalar (or array of the same shape as input array-like arguments) of,
-
type
real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128),
containing the approximate value of the inverse error function at the specified input point x. |
| [in] | x | : The input scalar (or array of the same shape as other array-like arguments) of the same type and kind as the output erfinv.
|
| [in] | abserr | : The input positive scalar (or array of the same shape as other array-like arguments) of the same type and kind as the output erfinv.
If present, the output approximate value for the inverse error function is guaranteed to be at most abserr away from the true value \ms{erf}^{-1}(x).
This guarantee is currently tested and validated up to 2\times10^{-26}.
A reasonable value could be epsilon(x)**0.66.
The current implementation of this generic interface contains three methods of computing the inverse error function corresponding to three levels of increasing accuracy,
-
For any
1.e-7 < abserr, the output erfinv will have at most an absolute error 1.e-7 with respect to theoretical value.
-
For any
2.e-24 < abserr, the output erfinv will have at most an absolute error 2.e-24 with respect to theoretical value.
-
For any
abserr < 2.e-24, the output erfinv is currently verified to have at most an absolute error 2.e-26 with respect to theoretical value.
For a wide range of input x values, the absolute error is practically orders of magnitude smaller than this verified upper limit for the error.
See the example illustrations below for more information.
|
Possible calling interfaces ⛓
Return the Inverse Error Function for an input real value in range as defined in the details sectio...
This module contains classes and procedures for computing the mathematical Inverse Error Function.
- Warning
- The condition
0 < abserr must hold for the corresponding input arguments.
The conditions -1 < x .and. x < 1 must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.
-
The
pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.
- See also
- getErfInv
setErfInv
getNormCDF
setNormCDF
getNormQuan
setNormQuan
getNormRand
setNormRand
getNormLogPDF
setNormLogPDF
Example usage ⛓
11 real(RKH),
allocatable :: erfinv(:), x(:)
13 type(display_type) :: disp
17 call disp%show(
"x = [real(RKH) :: 0., 0.5]")
18 x
= [
real(
RKH) ::
0.,
0.5]
21 call disp%show(
"call setResized(erfinv, size(x, 1, IK))")
23 call disp%show(
"call setErfInv(erfinv, x, abserr = epsilon(x))")
24 call setErfInv(erfinv, x, abserr
= epsilon(x))
32 call disp%show(
"x = .subadd. 1. - .subadd. epsilon(0.)")
33 x
= .subadd.
1. - .subadd.
epsilon(
0.)
36 call disp%show(
"call setResized(erfinv, size(x, 1, IK))")
38 call disp%show(
"call setErfInv(erfinv, x, abserr = epsilon(x))")
39 call setErfInv(erfinv, x, abserr
= epsilon(x))
47 call disp%show(
"x = [-.99, -.75, -0.5, -0.1, 0., .1, .5, .75, .99]")
48 x
= [
-.
99,
-.
75,
-0.5,
-0.1,
0., .
1, .
5, .
75, .
99]
51 call disp%show(
"call setResized(erfinv, size(x, 1, IK))")
53 call disp%show(
"call setErfInv(erfinv, x, abserr = epsilon(x))")
54 call setErfInv(erfinv, x, abserr
= epsilon(x))
68 integer(IK) ,
parameter :: NP
= 2000
69 integer :: fileUnit, i
70 real(RKG) :: erfval(NP), erfinv(NP)
72 call setLinSpace(erfval,
-1._RKG + sqrt(
epsilon(
0._RKG)),
1._RKG - sqrt(
epsilon(
0._RKG)))
74 open(newunit
= fileUnit, file
= "setErfInv.RK.txt")
75 call setErfInv(erfinv, erfval, abserr
= 100 * epsilon(
0._RKG))
77 write(fileUnit,
"(*(g0,:,' '))")
real(erfval(i), RKG),
real(erfinv(i), RKG)
83 open(newunit
= fileUnit, file
= "setErfInv.RKS.abserr.txt")
84 call setErfInv(erfinv, erfval, abserr
= real(
100 * epsilon(
0._RKG),
RKH))
86 write(fileUnit,
"(*(g0,:,' '))")
real(erfval(i), RKG),
real(erfval(i), RKG)
- erf(
real(erfinv(i),
RKB))
93 open(newunit
= fileUnit, file
= "setErfInv.RKD.abserr.txt")
94 call setErfInv(erfinv, erfval, abserr
= real(
100 * epsilon(
0._RKG),
RKH))
96 write(fileUnit,
"(*(g0,:,' '))")
real(erfval(i), RKG),
real(erfval(i), RKG)
- erf(
real(erfinv(i),
RKB))
103 open(newunit
= fileUnit, file
= "setErfInv.RKH.abserr.txt")
104 call setErfInv(erfinv, erfval, abserr
= real(
100 * epsilon(
0._RKG),
RKH))
106 write(fileUnit,
"(*(g0,:,' '))")
real(erfval(i), RKG),
real(erfval(i), RKG)
- erf(
real(erfinv(i),
RKB))
Allocate or resize (shrink or expand) an input allocatable scalar string or array of rank 1....
Return the linSpace output argument with size(linSpace) elements of evenly-spaced values over the int...
This is a generic method of the derived type display_type with pass attribute.
This is a generic method of the derived type display_type with pass attribute.
This module contains procedures and generic interfaces for resizing allocatable arrays of various typ...
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
This module contains classes and procedures for input/output (IO) or generic display operations on st...
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
integer, parameter LK
The default logical kind in the ParaMonte library: kind(.true.) in Fortran, kind(....
integer, parameter RKB
The scalar integer constant of intrinsic default kind, representing the Best-precision real kind supp...
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
integer, parameter RKD
The double precision real kind in Fortran mode. On most platforms, this is an 64-bit real kind.
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
integer, parameter RKH
The scalar integer constant of intrinsic default kind, representing the highest-precision real kind t...
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
This module contains procedures and generic interfaces for evaluating the mathematical operator acti...
Generate and return an object of type display_type.
Example Unix compile command via Intel ifort compiler ⛓
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example Windows Batch compile command via Intel ifort compiler ⛓
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
Example Unix / MinGW compile command via GNU gfortran compiler ⛓
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example output ⛓
2x
= [
real(
RKH) ::
0.,
0.5]
4+0.00000000000000000000000000000000000,
+0.500000000000000000000000000000000000
6call setErfInv(erfinv, x, abserr
= epsilon(x))
8-0.132513883613671435781879776977691272E-34,
+0.476936276204469873381418342335513784
10-0.149525905620586266620169289835968551E-34,
+0.499999999999999999999999989836624968
13x
= .subadd.
1. - .subadd.
epsilon(
0.)
15-0.999999880790710449218750000000000000,
+0.999999880790710449218750000000000000
17call setErfInv(erfinv, x, abserr
= epsilon(x))
19-3.74392116277679962488913660265320747,
+3.74392116277679962488913660265320747
21-0.999999880790710449218750000097940664,
+0.999999880790710449218750000097940664
24x
= [
-.
99,
-.
75,
-0.5,
-0.1,
0., .
1, .
5, .
75, .
99]
26-0.990000009536743164062500000000000000,
-0.750000000000000000000000000000000000,
-0.500000000000000000000000000000000000,
-0.100000001490116119384765625000000000,
+0.00000000000000000000000000000000000,
+0.100000001490116119384765625000000000,
+0.500000000000000000000000000000000000,
+0.750000000000000000000000000000000000,
+0.990000009536743164062500000000000000
28call setErfInv(erfinv, x, abserr
= epsilon(x))
30-1.82138660090027777498853581706459074,
-0.813419847597618541690289359089294846,
-0.476936276204469873381418342335513784,
-0.888559918253064817186753173353988263E-1,
-0.132513883613671435781879776977691272E-34,
+0.888559918253064817186753173353988263E-1,
+0.476936276204469873381418342335513784,
+0.813419847597618541690289359089294846,
+1.82138660090027777498853581706459074
32-0.990000009536743164062500001249670844,
-0.749999999999999999999999999531804119,
-0.499999999999999999999999989836624968,
-0.100000001490116119384765624995815857,
-0.149525905620586266620169289835968551E-34,
+0.100000001490116119384765624995815857,
+0.499999999999999999999999989836624968,
+0.749999999999999999999999999531804119,
+0.990000009536743164062500001249670844
Postprocessing of the example output ⛓
3import matplotlib.pyplot
as plt
12parent = os.path.basename(os.path.dirname(__file__))
13pattern = parent +
"*.txt"
15fileList = glob.glob(pattern)
18 df = pd.read_csv(file, delimiter =
" ")
20 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
23 for i
in range(1,len(df.values[0,:]+1)):
25 plt.plot( df.values[:, 0]
30 plt.xticks(fontsize = fontsize - 2)
31 plt.yticks(fontsize = fontsize - 2)
32 ax.set_xlabel(
"x", fontsize = fontsize)
34 nbit = file.split(
".")[1][2:]
35 label = [
r"x - erf(erfinv(x))"]
36 ax.set_ylabel(
"{}-bits Absolute Error".format(nbit), fontsize = fontsize)
38 label = [
r"erfinv(x)"]
39 ax.set_ylabel(
"Inverse Error Function", fontsize = fontsize)
41 plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
42 ax.tick_params(axis =
"y", which =
"minor")
43 ax.tick_params(axis =
"x", which =
"minor")
51 plt.savefig(file.replace(
".txt",
".png"))
Visualization of the example output ⛓
- Test:
- test_pm_mathErf
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
-
If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
-
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
- Copyright
- Computational Data Science Lab
- Author:
- Amir Shahmoradi, Nov 10, 2009, 8:53 PM, Michigan
Definition at line 340 of file pm_mathErf.F90.