Return the regularized Incomplete Beta Function I_x(\alpha, \beta) as defined in the details section of pm_mathBeta.
- Parameters
-
| [in] | betaInc | : The output scalar (or array of the same shape as other array-like arguments) of the same type and kind as the input argument x containing the regularized Incomplete Beta Function. |
| [in] | x | : The input scalar (or array of the same shape as other array-like arguments) of,
-
type
real of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128),
containing the value at which the function must be computed. |
| [in] | alpha | : The input scalar (or array of the same shape as other array-like arguments) of the same type and kind as x. |
| [in] | beta | : The input scalar (or array of the same shape as other array-like arguments) of the same type and kind as x. |
| [in] | logFuncBeta | : The input scalar (or array of the same shape as other array-like arguments) of the same type and kind as x, representing the natural logarithm of the Beta Function as returned by getLogBeta(alpha, beta).
Providing this argument can lead to significant runtime performance gains when the interface is called repeatedly for different x values but with identical alpha and beta. |
| [in] | signed | : The input scalar (or array of the same shape as other array-like arguments) of type logical of default kind LK.
-
If
signed = .false., the input x must be in range 0 <= x <= 1 and the output betaInc will be the expected incomplete Beta function in range 0 <= betaInc <= 1.
-
If
signed = .true., then the following rules hold:
-
If the condition
x < 0 holds, then the value x = 1 - x < 0 will be used instead of x.
-
If the output
betaInc is near 1, the output will be returned as betaInc = betaInc - 1 < 0 instead of betaInc.
Therefore, the user is expected to be aware of the convention and apply the necessary correction (addition by 1) before using the output value.
Specifying signed = .true. can lead to considerably more accurate calculations (by orders of magnitudes) for values of x and betaInc that are near 1.
The loss of precision near 1 occurs because of inadequate resolution of real number representations in digital computers near 1 which is orders of magnitude worse than the precision near 0.
|
| [in] | reltol | : The input scalar argument of the same type and kind as betaInc, representing the relative tolerance of integration in the definition of the Incomplete Beta function.
If the relative accuracy of integration reaches a value below this threshold, the computation of the Incomplete Beta function is assumed to have converged.
Specifying this argument will lead to brute-force numerical integration of the integrand of the Beta function to compute the integral.
This approach can be useful when the continued-fraction representation of the Incomplete Beta Function fails to converge or is extremely costly or a bound on the numerical error is needed.
Convergence failure or costly computations frequently occur for large values of alpha and beta.
This argument can be set to any positive value significantly larger (e.g., \times10000) than epsilon(real(0., kind(reltol)).
A good rule of thumb is to set reltol = epsilon(real(0, kind(integral)))**(2./3.).
The integration result is generally orders of magnitude more precise than the specified reltol.
(optional. If missing, the continued-fraction representation of the Incomplete Beta function will be used to approximate the output.) |
| [out] | info | : The output scalar (or array of the same shape as other array-like arguments) of type integer of default kind IK.
It is 0 if and only if the computation converges, otherwise,
-
if the input argument
reltol is missing, it is set to 1 to signal lack of convergence in the computation of the continued-fraction representation of the Incomplete Beta function.
Convergence fails if alpha or beta are too large, in which case a brute-force integration method by specifying the input argument reltol might resolve it.
-
if the input argument
reltol is present, it is set to the non-zero info output of getQuadErr to signal lack of convergence in the computation of the integral.
See the documentation of the output argument info of getQuadErr for possible output error codes and their meanings.
The failure may be resolved by increasing the preset value of MAX_ITER in the implementation.
|
- Returns
Possible calling interfaces ⛓
call setBetaInc(betaInc, x, alpha, beta, logFuncBeta, signed, info)
call setBetaInc(betaInc, x, alpha, beta, logFuncBeta, reltol, signed, info)
Return the regularized Incomplete Beta Function as defined in the details section of pm_mathBeta.
This module contains classes and procedures for computing the mathematical Beta Function and its inve...
- Warning
- The conditions
0 <= x .and. x <= 1 must hold for the corresponding input arguments.
The conditions 0 < alpha .and. 0 < beta must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.
-
The
pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds. The procedures of this generic interface are always impure when the input argument reltol is present.
- See also
- getLogBeta
setBetaInc
getBetaLogPDF
Example usage ⛓
12 integer(IK) :: info(
3)
13 real(RKG) :: betaInc(
3), alpha, beta, reltol
14 real(RKG) ,
allocatable :: alphas(:), betas(:)
15 type(display_type) :: disp
19 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
20 call disp%show(
"! Compute the regularized (lower) Incomplete Beta Function using its series representation.")
21 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
25 call disp%show(
"alpha = 2.; beta = 3.")
27 call disp%show(
"call setBetaInc(betaInc(1), 0._RKG, alpha, beta, getLogBeta(alpha, beta), signed = .false._LK, info = info(1))")
28 call setBetaInc(betaInc(
1),
0._RKG, alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info(
1))
29 call disp%show(
.not."call setAsserted( info(1) < 0)")
36 call disp%show(
"alpha = 2.; beta = 3.")
38 call disp%show(
"call setBetaInc(betaInc(1), .5_RKG, alpha, beta, getLogBeta(alpha, beta), signed = .false._LK, info = info(1)) ! 0.6875")
39 call setBetaInc(betaInc(
1), .
5_RKG, alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info(
1))
40 call disp%show(
.not."call setAsserted( info(1) < 0)")
47 call disp%show(
"alpha = 2.; beta = 3.")
49 call disp%show(
"call setBetaInc(betaInc(1), 1._RKG, alpha, beta, getLogBeta(alpha, beta), signed = .false._LK, info = info(1))")
50 call setBetaInc(betaInc(
1),
1._RKG, alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info(
1))
51 call disp%show(
.not."call setAsserted( info(1) < 0)")
58 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
59 call disp%show(
"! Compute the regularized (lower) Incomplete Beta Function for a vector of points.")
60 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
64 call disp%show(
"alpha = 2.; beta = 3.")
66 call disp%show(
"call setBetaInc(betaInc, [0._RKG, 0.5_RKG, 1._RKG], alpha, beta, getLogBeta(alpha, beta), signed = .false._LK, info = info)")
67 call setBetaInc(betaInc, [
0._RKG,
0.5_RKG,
1._RKG], alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info)
75 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
76 call disp%show(
"! Compute the regularized Incomplete Beta Function for a vector of input parameters.")
77 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
81 call disp%show(
"alphas = [real(RKG) :: 0.1, 1., 10.]; beta = 3.")
82 alphas
= [
real(RKG) ::
0.1,
1.,
10.]; beta
= 3.
83 call disp%show(
"call setBetaInc(betaInc, [0._RKG, 0.5_RKG, 1._RKG], alphas, beta, getLogBeta(alphas, beta), signed = .false._LK, info = info)")
84 call setBetaInc(betaInc, [
0._RKG,
0.5_RKG,
1._RKG], alphas, beta,
getLogBeta(alphas, beta), signed
= .false._LK, info
= info)
92 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
93 call disp%show(
"! Compute the regularized (lower) Incomplete Beta Function using brute-force integration.")
94 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
98 call disp%show(
"reltol = epsilon(reltol)**.7")
99 reltol
= epsilon(reltol)
**.
7
100 call disp%show(
"alphas = 5000.**[1, -1]; betas = 5000.**[1, -1]")
101 alphas
= 5000.**[
1,
-1]; betas
= 5000.**[
1,
-1]
102 call disp%show(
"call setBetaInc(betaInc(1:2), .5_RKG, alphas, betas, getLogBeta(alphas, betas), reltol, signed = .false._LK, info = info(1:2))")
103 call setBetaInc(betaInc(
1:
2), .
5_RKG, alphas, betas,
getLogBeta(alphas, betas), reltol, signed
= .false._LK, info
= info(
1:
2))
111 call disp%show(
"reltol = epsilon(reltol)**.7")
112 reltol
= epsilon(reltol)
**.
7
115 call disp%show(
"alphas = 5000.**[1, -1]; betas = 5000.**[1, -1]")
116 alphas
= 5000.**[
1,
-1]; betas
= 5000.**[
1,
-1]
117 call disp%show(
"call setBetaInc(betaInc(1:2), .5_RKG, alphas, betas, getLogBeta(alphas, betas), signed = .false._LK, info = info(1:2))")
118 call setBetaInc(betaInc(
1:
2), .
5_RKG, alphas, betas,
getLogBeta(alphas, betas), signed
= .false._LK, info
= info(
1:
2))
146 integer(IK) ,
parameter :: nx
= 1000
147 real(RKG) ,
parameter :: alphas(
*)
= [
0.1_RKG,
10._RKG,
1._RKG,
0.1_RKG,
10._RKG], betas(
*)
= [
0.1_RKG,
0.1_RKG,
1._RKG,
10._RKG,
10._RKG]
148 real(RKG) :: betaInc(
max(
size(alphas),
size(betas)))
149 integer(IK) :: fileUnit, i, info(
size(betaInc))
151 call setLinSpace(x,
0._RKG,
1._RKG, fopen
= .true._LK, lopen
= .true._LK)
152 open(newunit
= fileUnit, file
= "setBetaInc.RK.txt")
154 call setBetaInc(betaInc, x(i), alphas, betas,
getLogBeta(alphas, betas), signed
= .false._LK, info
= info)
155 if (
any(info
/= 0))
error stop
156 write(fileUnit,
"(*(g0,:,','))") x(i), betaInc
Return the linSpace output argument with size(linSpace) elements of evenly-spaced values over the int...
Verify the input assertion holds and if it does not, print the (optional) input message on stdout and...
Generate and return an object of type stop_type with the user-specified input attributes.
This is a generic method of the derived type display_type with pass attribute.
Generate and return the natural logarithm of the Beta Function as defined in the details section of ...
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
This module contains classes and procedures for reporting and handling errors.
This module contains classes and procedures for input/output (IO) or generic display operations on st...
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
integer, parameter LK
The default logical kind in the ParaMonte library: kind(.true.) in Fortran, kind(....
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
integer, parameter RKH
The scalar integer constant of intrinsic default kind, representing the highest-precision real kind t...
Generate and return an object of type display_type.
Example Unix compile command via Intel ifort compiler ⛓
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example Windows Batch compile command via Intel ifort compiler ⛓
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
Example Unix / MinGW compile command via GNU gfortran compiler ⛓
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example output ⛓
8call setBetaInc(betaInc(
1),
0._RKG, alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info(
1))
11+0.00000000000000000000000000000000000
15call setBetaInc(betaInc(
1), .
5_RKG, alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info(
1))
18+0.687500000000000000000000000000000096
22call setBetaInc(betaInc(
1),
1._RKG, alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info(
1))
25+1.00000000000000000000000000000000000
34call setBetaInc(betaInc, [
0._RKG,
0.5_RKG,
1._RKG], alpha, beta,
getLogBeta(alpha, beta), signed
= .false._LK, info
= info)
38+0.00000000000000000000000000000000000,
+0.687500000000000000000000000000000096,
+1.00000000000000000000000000000000000
46alphas
= [
real(RKG) ::
0.1,
1.,
10.]; beta
= 3.
47call setBetaInc(betaInc, [
0._RKG,
0.5_RKG,
1._RKG], alphas, beta,
getLogBeta(alphas, beta), signed
= .false._LK, info
= info)
51+0.00000000000000000000000000000000000,
+0.875000000000000000000000000000000000,
+1.00000000000000000000000000000000000
59reltol
= epsilon(reltol)
**.
7
60alphas
= 5000.**[
1,
-1]; betas
= 5000.**[
1,
-1]
61call setBetaInc(betaInc(
1:
2), .
5_RKG, alphas, betas,
getLogBeta(alphas, betas), reltol, signed
= .false._LK, info
= info(
1:
2))
65+0.499999999999999999999999999995890258,
+0.499999999999999999999999999656137679
68reltol
= epsilon(reltol)
**.
7
70+0.250754503649549880673038532701962290E-23
71alphas
= 5000.**[
1,
-1]; betas
= 5000.**[
1,
-1]
72call setBetaInc(betaInc(
1:
2), .
5_RKG, alphas, betas,
getLogBeta(alphas, betas), signed
= .false._LK, info
= info(
1:
2))
76+0.499999999999999999999999999995924251,
+0.499999999999999999999999999999999567
Postprocessing of the example output ⛓
3import matplotlib.pyplot
as plt
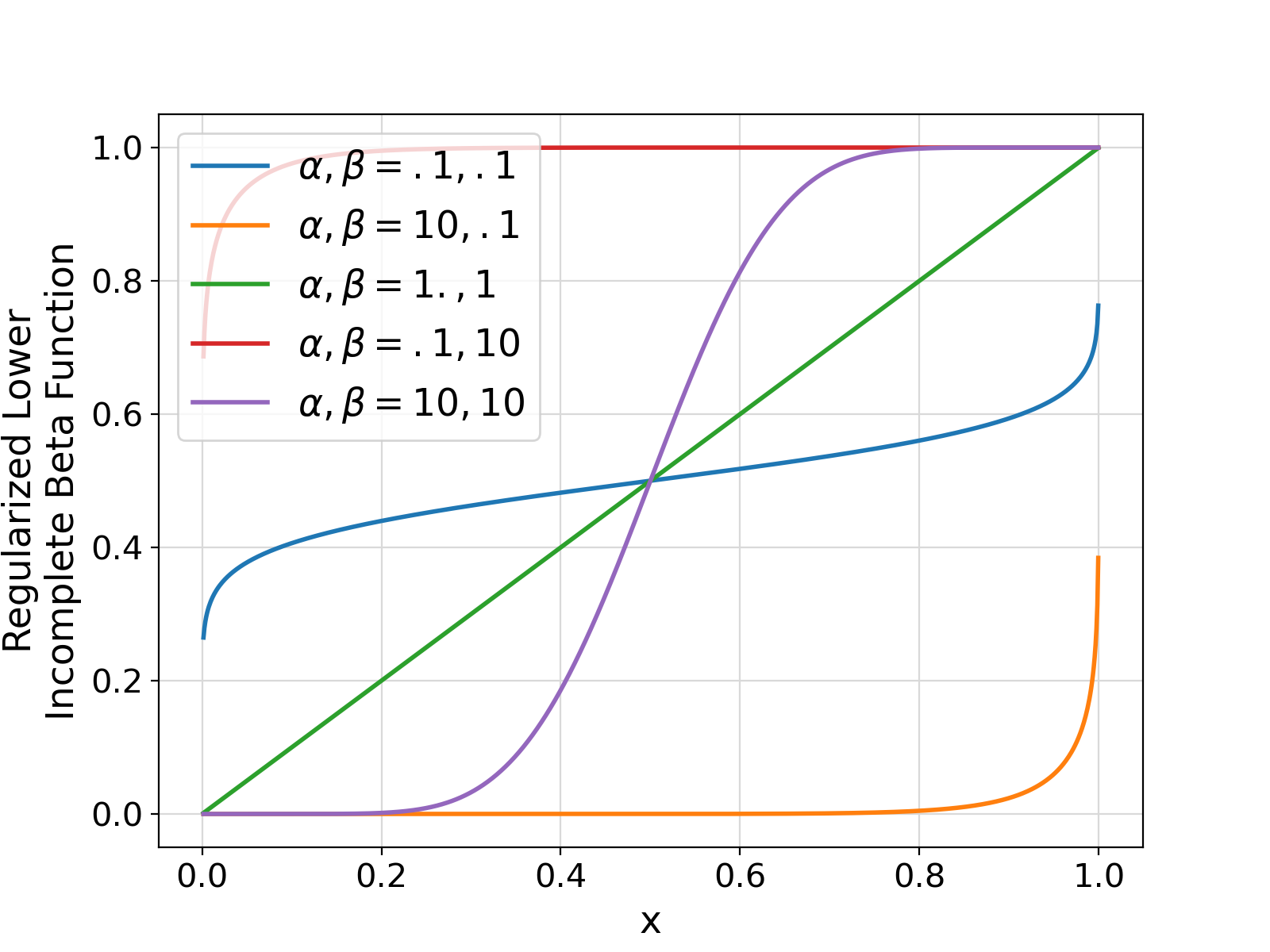
16label = [
r"$\alpha, \beta = .1, .1$"
17 ,
r"$\alpha, \beta = 10, .1$"
18 ,
r"$\alpha, \beta = 1., 1.$"
19 ,
r"$\alpha, \beta = .1, 10$"
20 ,
r"$\alpha, \beta = 10, 10$"
23pattern =
"*." + kind +
".txt"
24fileList = glob.glob(pattern)
27 df = pd.read_csv(fileList[0], delimiter =
",")
29 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
32 for i
in range(1,len(df.values[0,:]+1)):
34 plt.plot( df.values[:, 0]
39 plt.xticks(fontsize = fontsize - 2)
40 plt.yticks(fontsize = fontsize - 2)
41 ax.set_xlabel(
"x", fontsize = fontsize)
42 ax.set_ylabel(
"Regularized Lower\nIncomplete Beta Function", fontsize = fontsize)
46 plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
47 ax.tick_params(axis =
"y", which =
"minor")
48 ax.tick_params(axis =
"x", which =
"minor")
56 plt.savefig(fileList[0].replace(
".txt",
".png"))
60 sys.exit(
"Ambiguous file list exists.")
Visualization of the example output ⛓
- Test:
- test_pm_mathBeta
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
-
If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
-
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
- Copyright
- Computational Data Science Lab
- Author:
- Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 442 of file pm_mathBeta.F90.