ParaMonte Fortran 2.0.0
Parallel Monte Carlo and Machine Learning Library
See the latest version documentation.
pm_distGenGamma::getGenGammaLogPDFNF Interface Reference

Generate and return the natural logarithm of the normalization factor of the Probability Density Function (PDF) of the GenGamma distribution.
More...

Detailed Description

Generate and return the natural logarithm of the normalization factor of the Probability Density Function (PDF) of the GenGamma distribution.

The normalization factor of the GenGamma PDF is defined as \(\eta = 1 / (\sigma \omega \Gamma(\kappa))\) where \((\omega, \kappa)\) are the scale and shape parameters of the GenGamma distribution, respectively.
For more information, see the documentation of pm_distGenGamma.

Parameters
[in]kappa: The input scalar or array of the same shape as other array-like arguments, containing the shape parameter ( \(\kappa\)) of the distribution.
[in]invOmega: The input scalar or array of the same shape as other array-like arguments, containing the inverse of the second shape parameter ( \(\omega\)) of the distribution.
(optional, default = 1.. It must be present if invSigma is also present.)
[in]invSigma: The input scalar or array of the same shape as other array-valued arguments, containing the inverse of the scale parameter ( \(\sigma\)) of the distribution.
(optional, default = 1.)
Returns
logPDFNF : The output scalar or array of the same shape as array-like input arguments, of the same type, kind, and highest rank as the input arguments containing the natural logarithm of the normalization factor of the distribution.


Possible calling interfaces ⛓

use pm_distGenGamma, only: getGenGammaLogPDFNF
logPDFNF = getGenGammaLogPDFNF(kappa)
logPDFNF = getGenGammaLogPDFNF(kappa, invOmega)
logPDFNF = getGenGammaLogPDFNF(kappa, invOmega, invSigma)
pm_distGenGamma::getGenGammaLogPDFNF
Generate and return the natural logarithm of the normalization factor of the Probability Density Func...
Definition: pm_distGenGamma.F90:250
pm_distGenGamma
This module contains classes and procedures for computing various statistical quantities related to t...
Definition: pm_distGenGamma.F90:129
Warning
The conditions kappa > 0, invOmega > 0, and invSigma > 0 must hold for the corresponding input arguments.
These conditions are verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.
The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.
Remarks
The procedures under discussion are elemental.
These procedures are particularly useful and needed in computing the PDF of the distribution.
The logic behind pre-computing the normalization factor is to speed up the calculations since the normalization factor contains log() and log_gamma() computations which are computationally costly operations.
See the benchmark below for more details.
See also
getGenGammaLogPDF
setGenGammaLogPDF


Example usage ⛓

1program example
2
3 use pm_kind, only: IK
4 use pm_kind, only: SK
5 use pm_kind, only: RK => RKS ! all other real kinds are also supported.
6 use pm_io, only: display_type
7 use pm_arraySpace, only: getLinSpace
8 use pm_arraySpace, only: setLinSpace
9 use pm_distGenGamma, only: getGenGammaLogPDFNF
10
11 implicit none
12
13 integer(IK) , parameter :: NP = 1000_IK
14 real(RK) , allocatable :: invSigma(:), invOmega(:), Kappa(:), logPDFNF(:)
15
16 type(display_type) :: disp
17 disp = display_type(file = "main.out.F90")
18
19 Kappa = getLinSpace(0.01_RK, 10._RK, count = NP)
20 invOmega = getLinSpace(0.1_RK, 10._RK, count = NP)
21 invSigma = getLinSpace(0.1_RK, 10._RK, count = NP)
22 allocate(logPDFNF, mold = Kappa)
23
24 call disp%skip()
25 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
26 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
27 call disp%show("! Compute the natural logarithm of the normalization factor of the GenGamma distribution PDF.")
28 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
29 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
30 call disp%skip()
31
32 call disp%skip()
33 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
34 call disp%show("! Compute the PDF at an input scalar real value.")
35 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
36 call disp%skip()
37
38 call disp%skip()
39 call disp%show("Kappa(1)")
40 call disp%show( Kappa(1) )
41 call disp%show("logPDFNF(1) = getGenGammaLogPDFNF(kappa = Kappa(1))")
42 logPDFNF(1) = getGenGammaLogPDFNF(kappa = Kappa(1))
43 call disp%show("logPDFNF(1)")
44 call disp%show( logPDFNF(1) )
45 call disp%skip()
46
47 call disp%skip()
48 call disp%show("Kappa(1)")
49 call disp%show( Kappa(1) )
50 call disp%show("invOmega(1)")
51 call disp%show( invOmega(1) )
52 call disp%show("logPDFNF(1) = getGenGammaLogPDFNF(Kappa(1), invOmega(1))")
53 logPDFNF(1) = getGenGammaLogPDFNF(Kappa(1), invOmega(1))
54 call disp%show("logPDFNF(1)")
55 call disp%show( logPDFNF(1) )
56 call disp%skip()
57
58 call disp%skip()
59 call disp%show("Kappa(1)")
60 call disp%show( Kappa(1) )
61 call disp%show("invOmega(1)")
62 call disp%show( invOmega(1) )
63 call disp%show("invSigma(1)")
64 call disp%show( invSigma(1) )
65 call disp%show("logPDFNF(1) = getGenGammaLogPDFNF(Kappa(1), invOmega(1), invSigma(1))")
66 logPDFNF(1) = getGenGammaLogPDFNF(Kappa(1), invOmega(1), invSigma(1))
67 call disp%show("logPDFNF(1)")
68 call disp%show( logPDFNF(1) )
69 call disp%skip()
70
71 call disp%skip()
72 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
73 call disp%show("! Compute the PDF at at a mix of scalar and vector input values.")
74 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
75 call disp%skip()
76
77 call disp%skip()
78 call disp%show("Kappa(1:NP:NP/5)")
79 call disp%show( Kappa(1:NP:NP/5) )
80 call disp%show("logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5))")
81 logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5))
82 call disp%show("logPDFNF(1:NP:NP/5)")
83 call disp%show( logPDFNF(1:NP:NP/5) )
84 call disp%skip()
85
86 call disp%skip()
87 call disp%show("Kappa(1:NP:NP/5)")
88 call disp%show( Kappa(1:NP:NP/5) )
89 call disp%show("logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), 1._RK)")
90 logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), 1._RK)
91 call disp%show("logPDFNF(1:NP:NP/5)")
92 call disp%show( logPDFNF(1:NP:NP/5) )
93 call disp%skip()
94
95 call disp%skip()
96 call disp%show("Kappa(1:NP:NP/5)")
97 call disp%show( Kappa(1:NP:NP/5) )
98 call disp%show("invOmega(1:NP:NP/5)")
99 call disp%show( invOmega(1:NP:NP/5) )
100 call disp%show("logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(1._RK, invOmega(1:NP:NP/5))")
101 logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(1._RK, invOmega(1:NP:NP/5))
102 call disp%show("logPDFNF(1:NP:NP/5)")
103 call disp%show( logPDFNF(1:NP:NP/5) )
104 call disp%skip()
105
106 call disp%skip()
107 call disp%show("Kappa(1:NP:NP/5)")
108 call disp%show( Kappa(1:NP:NP/5) )
109 call disp%show("invOmega(1:NP:NP/5)")
110 call disp%show( invOmega(1:NP:NP/5) )
111 call disp%show("logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), invOmega(1:NP:NP/5))")
112 logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), invOmega(1:NP:NP/5))
113 call disp%show("logPDFNF(1:NP:NP/5)")
114 call disp%show( logPDFNF(1:NP:NP/5) )
115 call disp%skip()
116
117 call disp%skip()
118 call disp%show("Kappa(1:NP:NP/5)")
119 call disp%show( Kappa(1:NP:NP/5) )
120 call disp%show("invOmega(1:NP:NP/5)")
121 call disp%show( invOmega(1:NP:NP/5) )
122 call disp%show("invSigma(1:NP:NP/5)")
123 call disp%show( invSigma(1:NP:NP/5) )
124 call disp%show("logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), invOmega(1:NP:NP/5), invSigma(1:NP:NP/5))")
125 logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), invOmega(1:NP:NP/5), invSigma(1:NP:NP/5))
126 call disp%show("logPDFNF(1:NP:NP/5)")
127 call disp%show( logPDFNF(1:NP:NP/5) )
128 call disp%skip()
129
130 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
131 ! Output an example array for visualization.
132 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
133
134 block
135 integer :: fileUnit, i
136 logPDFNF = getGenGammaLogPDFNF(Kappa)
137 open(newunit = fileUnit, file = "getGenGammaLogPDFNF.RK.txt")
138 write(fileUnit,"(2(g0,:,' '))") (Kappa(i), exp(logPDFNF(i)), i = 1, size(logPDFNF))
139 close(fileUnit)
140 end block
141
142end program example
pm_arraySpace::getLinSpace
Generate count evenly spaced points over the interval [x1, x2] if x1 < x2, or [x2,...
Definition: pm_arraySpace.F90:108
pm_arraySpace::setLinSpace
Return the linSpace output argument with size(linSpace) elements of evenly-spaced values over the int...
Definition: pm_arraySpace.F90:324
pm_io::show
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11726
pm_io::skip
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11508
pm_arraySpace
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
Definition: pm_arraySpace.F90:33
pm_io
This module contains classes and procedures for input/output (IO) or generic display operations on st...
Definition: pm_io.F90:252
pm_io::disp
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
Definition: pm_io.F90:11393
pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268
pm_kind::RK
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
Definition: pm_kind.F90:543
pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540
pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539
pm_kind::RKS
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Definition: pm_kind.F90:567
pm_io::display_type
Generate and return an object of type display_type.
Definition: pm_io.F90:10282

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh
2rm main.exe
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
4./main.exe

Example output ⛓
1
2!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
3!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
4! Compute the natural logarithm of the normalization factor of the GenGamma distribution PDF.
5!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
6!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
7
8
9!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
10! Compute the PDF at an input scalar real value.
11!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
12
13
14Kappa(1)
15+0.999999978E-2
16logPDFNF(1) = getGenGammaLogPDFNF(kappa = Kappa(1))
17logPDFNF(1)
18-4.59948015
19
20
21Kappa(1)
22+0.999999978E-2
23invOmega(1)
24+0.100000001
25logPDFNF(1) = getGenGammaLogPDFNF(Kappa(1), invOmega(1))
26logPDFNF(1)
27-6.90206528
28
29
30Kappa(1)
31+0.999999978E-2
32invOmega(1)
33+0.100000001
34invSigma(1)
35+0.100000001
36logPDFNF(1) = getGenGammaLogPDFNF(Kappa(1), invOmega(1), invSigma(1))
37logPDFNF(1)
38-9.20465088
39
40
41!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
42! Compute the PDF at at a mix of scalar and vector input values.
43!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
44
45
46Kappa(1:NP:NP/5)
47+0.999999978E-2, +2.00999999, +4.01000023, +6.01000023, +8.01000023
48logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5))
49logPDFNF(1:NP:NP/5)
50-4.59948015, -0.426001893E-2, -1.80433512, -4.80456209, -8.54532528
51
52
53Kappa(1:NP:NP/5)
54+0.999999978E-2, +2.00999999, +4.01000023, +6.01000023, +8.01000023
55logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), 1._RK)
56logPDFNF(1:NP:NP/5)
57-4.59948015, -0.426001893E-2, -1.80433512, -4.80456209, -8.54532528
58
59
60Kappa(1:NP:NP/5)
61+0.999999978E-2, +2.00999999, +4.01000023, +6.01000023, +8.01000023
62invOmega(1:NP:NP/5)
63+0.100000001, +2.08198190, +4.06396389, +6.04594564, +8.02792740
64logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(1._RK, invOmega(1:NP:NP/5))
65logPDFNF(1:NP:NP/5)
66-2.30258512, +0.733320296, +1.40215886, +1.79938793, +2.08292627
67
68
69Kappa(1:NP:NP/5)
70+0.999999978E-2, +2.00999999, +4.01000023, +6.01000023, +8.01000023
71invOmega(1:NP:NP/5)
72+0.100000001, +2.08198190, +4.06396389, +6.04594564, +8.02792740
73logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), invOmega(1:NP:NP/5))
74logPDFNF(1:NP:NP/5)
75-6.90206528, +0.729060292, -0.402176261, -3.00517416, -6.46239901
76
77
78Kappa(1:NP:NP/5)
79+0.999999978E-2, +2.00999999, +4.01000023, +6.01000023, +8.01000023
80invOmega(1:NP:NP/5)
81+0.100000001, +2.08198190, +4.06396389, +6.04594564, +8.02792740
82invSigma(1:NP:NP/5)
83+0.100000001, +2.08198190, +4.06396389, +6.04594564, +8.02792740
84logPDFNF(1:NP:NP/5) = getGenGammaLogPDFNF(Kappa(1:NP:NP/5), invOmega(1:NP:NP/5), invSigma(1:NP:NP/5))
85logPDFNF(1:NP:NP/5)
86-9.20465088, +1.46238065, +0.999982595, -1.20578623, -4.37947273
87
88

Postprocessing of the example output ⛓
1#!/usr/bin/env python
2
3import matplotlib.pyplot as plt
4import pandas as pd
5import numpy as np
6import glob
7import sys
8
9fontsize = 17
10
11marker ={ "CK" : "-"
12 , "IK" : "."
13 , "RK" : "-"
14 }
15xlab = { "CK" : r"shape parameter: $\kappa$ ( real/imaginary )"
16 , "IK" : r"shape parameter: $\kappa$ ( integer-valued )"
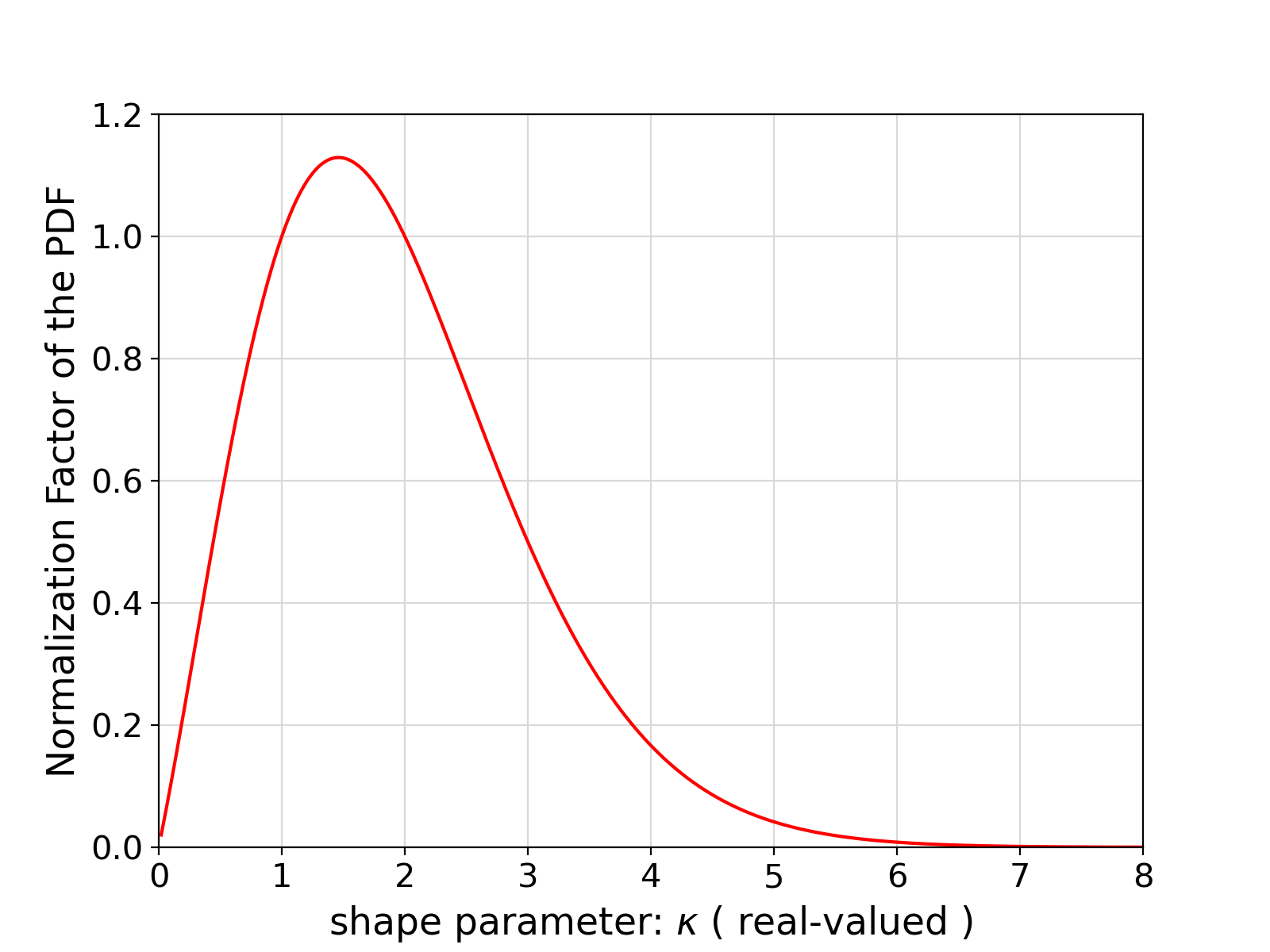
17 , "RK" : r"shape parameter: $\kappa$ ( real-valued )"
18 }
19
20for kind in ["IK", "CK", "RK"]:
21
22 pattern = "*." + kind + ".txt"
23 fileList = glob.glob(pattern)
24 if len(fileList) == 1:
25
26 df = pd.read_csv(fileList[0], delimiter = " ")
27
28 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
29 ax = plt.subplot()
30
31 if kind == "CK":
32 plt.plot( df.values[:, 0]
33 , df.values[:,2]
34 , marker[kind]
35 , color = "r"
36 )
37 plt.plot( df.values[:, 1]
38 , df.values[:,3]
39 , marker[kind]
40 , color = "blue"
41 )
42 else:
43 plt.plot( df.values[:, 0]
44 , df.values[:, 1]
45 , marker[kind]
46 , color = "r"
47 )
48
49 plt.xticks(fontsize = fontsize - 2)
50 plt.yticks(fontsize = fontsize - 2)
51 ax.set_xlabel(xlab[kind], fontsize = fontsize)
52 ax.set_ylabel("Normalization Factor of the PDF", fontsize = fontsize)
53 ax.set_xlim([0, 8.])
54 ax.set_ylim([0, 1.2])
55
56 plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")
57 ax.tick_params(axis = "y", which = "minor")
58 ax.tick_params(axis = "x", which = "minor")
59
60 plt.savefig(fileList[0].replace(".txt",".png"))
61
62 elif len(fileList) > 1:
63
64 sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓
Test:
test_pm_distGenGamma
Todo:
Normal Priority: This generic interface can be extended to complex arguments.


Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

  1. If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
  2. If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright
Computational Data Science Lab
Author:
Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan

Definition at line 250 of file pm_distGenGamma.F90.

The documentation for this interface was generated from the following file: