Generate and return the natural logarithm of the normalization factor of the Probability Density Function (PDF) of the ExpGamma distribution.
More...
Generate and return the natural logarithm of the normalization factor of the Probability Density Function (PDF) of the ExpGamma distribution.
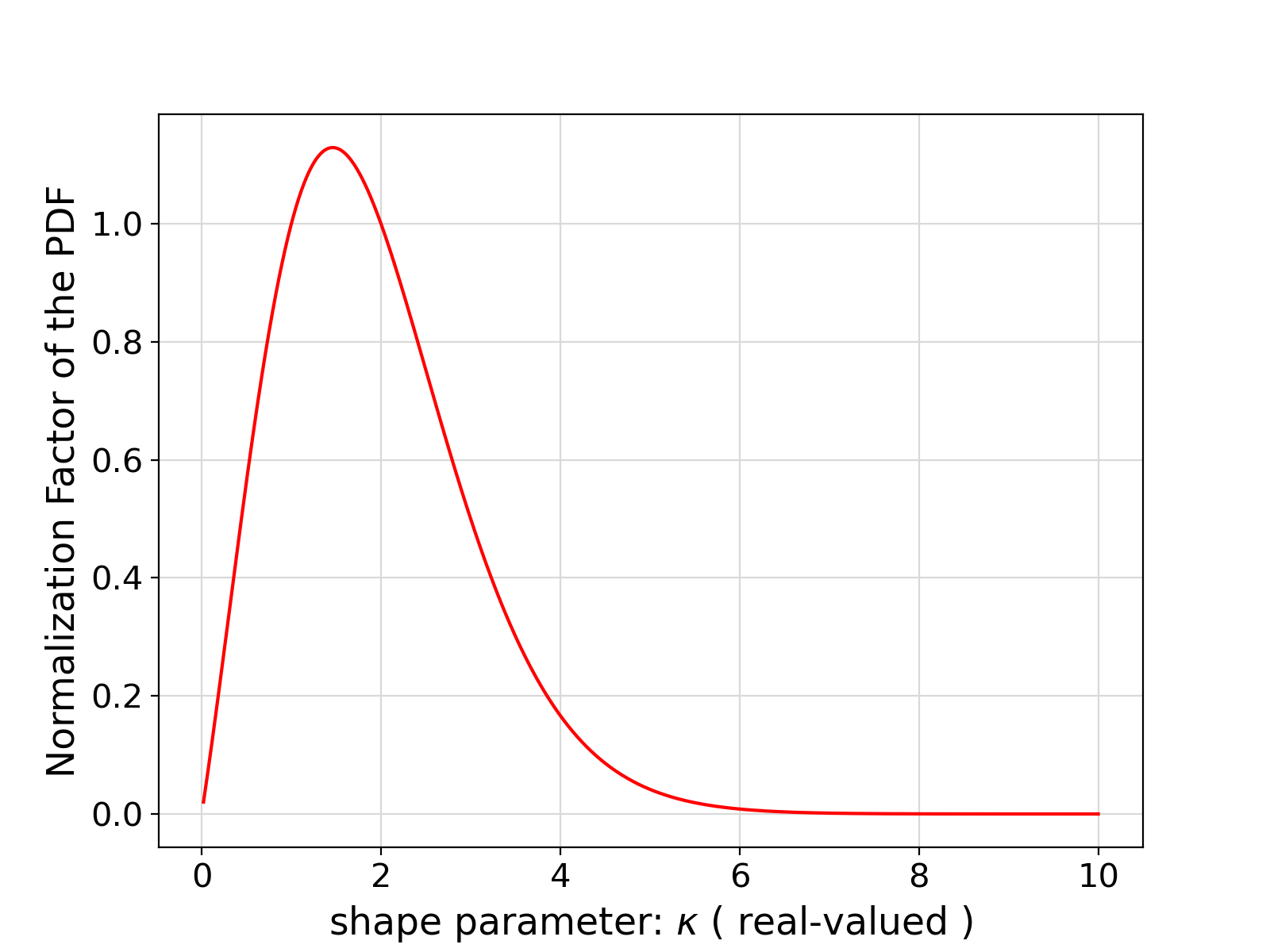
The normalization factor of the ExpGamma PDF is defined as \eta = 1 / \Gamma(\kappa) where \kappa is the shape parameter of the ExpGamma distribution.
For more information, see the documentation of pm_distExpGamma.
- Parameters
-
| [in] | kappa | : The input scalar or array of the same shape as other array-like arguments, containing the shape parameter ( \kappa) of the distribution.
|
- Returns
logPDFNF : The output scalar or array of the same shape as array-like input arguments, of the same type, kind, and highest rank as the input arguments containing the natural logarithm of the normalization factor of the distribution.
Possible calling interfaces ⛓
Generate and return the natural logarithm of the normalization factor of the Probability Density Func...
This module contains classes and procedures for computing various statistical quantities related to t...
- Warning
- The
pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.
- See also
- setExpGammaLogPDF
setExpGammaLogPDF
Example usage ⛓
13 integer(IK) ,
parameter :: NP
= 1000_IK
14 real(RK) ,
allocatable :: logPDFNF(:), Kappa(:)
16 type(display_type) :: disp
20 allocate(logPDFNF,
mold = Kappa)
23 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
24 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
25 call disp%show(
"! Compute the natural logarithm of the normalization factor of the ExpGamma distribution PDF.")
26 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
27 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
31 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
32 call disp%show(
"! Compute the PDF at an input scalar real value.")
33 call disp%show(
"!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
39 call disp%show(
"logPDFNF(1:NP:NP/5) = getExpGammaLogPDFNF(1._RK)")
41 call disp%show(
"logPDFNF(1:NP:NP/5)")
42 call disp%show( logPDFNF(
1:NP:NP
/5) )
48 call disp%show(
"logPDFNF(1) = getExpGammaLogPDFNF(kappa = Kappa(1))")
57 call disp%show(
"logPDFNF(1:NP:NP/5) = getExpGammaLogPDFNF(Kappa(1:NP:NP/5))")
59 call disp%show(
"logPDFNF(1:NP:NP/5)")
60 call disp%show( logPDFNF(
1:NP:NP
/5) )
71 integer :: fileUnit, i
73 open(newunit
= fileUnit, file
= "getExpGammaLogPDFNF.RK.txt")
74 write(fileUnit,
"(2(g0,:,' '))") (Kappa(i),
exp(logPDFNF(i)), i
= 1,
size(logPDFNF))
Generate count evenly spaced points over the interval [x1, x2] if x1 < x2, or [x2,...
Return the linSpace output argument with size(linSpace) elements of evenly-spaced values over the int...
This is a generic method of the derived type display_type with pass attribute.
This is a generic method of the derived type display_type with pass attribute.
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
This module contains classes and procedures for input/output (IO) or generic display operations on st...
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Generate and return an object of type display_type.
Example Unix compile command via Intel ifort compiler ⛓
3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example Windows Batch compile command via Intel ifort compiler ⛓
2set PATH=..\..\..\lib;%PATH%
3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe
Example Unix / MinGW compile command via GNU gfortran compiler ⛓
3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe
Example output ⛓
15+0.999999978E-2,
+2.00999999,
+4.01000023,
+6.01000023,
+8.01000023
18-0.00000000,
-0.00000000,
-0.00000000,
-0.00000000,
-0.00000000
29+0.999999978E-2,
+2.00999999,
+4.01000023,
+6.01000023,
+8.01000023
32-4.59948015,
-0.426001893E-2,
-1.80433512,
-4.80456209,
-8.54532528
Postprocessing of the example output ⛓
3import matplotlib.pyplot
as plt
15xlab = {
"CK" :
r"shape parameter: $\kappa$ ( real/imaginary )"
16 ,
"IK" :
r"shape parameter: $\kappa$ ( integer-valued )"
17 ,
"RK" :
r"shape parameter: $\kappa$ ( real-valued )"
20for kind
in [
"IK",
"CK",
"RK"]:
22 pattern =
"*." + kind +
".txt"
23 fileList = glob.glob(pattern)
24 if len(fileList) == 1:
26 df = pd.read_csv(fileList[0], delimiter =
" ")
28 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)
32 plt.plot( df.values[:, 0]
37 plt.plot( df.values[:, 1]
43 plt.plot( df.values[:, 0]
49 plt.xticks(fontsize = fontsize - 2)
50 plt.yticks(fontsize = fontsize - 2)
51 ax.set_xlabel(xlab[kind], fontsize = fontsize)
52 ax.set_ylabel(
"Normalization Factor of the PDF", fontsize = fontsize)
54 plt.grid(visible =
True, which =
"both", axis =
"both", color =
"0.85", linestyle =
"-")
55 ax.tick_params(axis =
"y", which =
"minor")
56 ax.tick_params(axis =
"x", which =
"minor")
58 plt.savefig(fileList[0].replace(
".txt",
".png"))
60 elif len(fileList) > 1:
62 sys.exit(
"Ambiguous file list exists.")
Visualization of the example output ⛓
- Test:
- test_pm_distExpGamma
- Todo:
- Normal Priority: This generic interface can be extended to
complex arguments.
Final Remarks ⛓
If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.
-
If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
-
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.
This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.
- Copyright
- Computational Data Science Lab
- Author:
- Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan
Definition at line 198 of file pm_distExpGamma.F90.