Generate and return the Cumulative Distribution Function (CDF) of the ExpGamma distribution for an input x within the support of the distribution $x \in (-\infty,+\infty)$. More...

Detailed Description

Generate and return the Cumulative Distribution Function (CDF) of the ExpGamma distribution for an input x within the support of the distribution $x \in (-\infty,+\infty)$.

See the documentation of pm_distExpGamma for more information on the ExpGamma CDF.

Parameters

[in]	x	: The input scalar or array of the same shape as other array like arguments, of type `real` of kind any supported by the processor (e.g., RK, RK32, RK64, or RK128), containing the values at which the CDF must be computed.
[in]	kappa	: The input scalar or array of the same shape as other array-like arguments, of the same type and kind as `x`, containing the shape parameter of the distribution. (optional, default = `1.`)
[in]	logSigma	: The input scalar or array of the same shape as other array-like arguments, of the same type and kind as `x`, containing the location parameter of the distribution. (optional, default = `1.`)

Returns: cdf : The output scalar or array of the same shape as any input array-like argument, of the same type and kind the input argument x, containing the CDF of the distribution at the specified x.

Possible calling interfaces ⛓

: use pm_distExpGamma, only: getExpGammaCDF

cdf = getExpGammaCDF(x, kappa = kappa, logSigma = logSigma)

pm_distExpGamma::getExpGammaCDF
Generate and return the Cumulative Distribution Function (CDF) of the ExpGamma distribution for an in...
Definition: pm_distExpGamma.F90:720

pm_distExpGamma
This module contains classes and procedures for computing various statistical quantities related to t...
Definition: pm_distExpGamma.F90:91

Warning: The condition kappa > 0 must hold for the corresponding input arguments.
This condition is verified only if the library is built with the preprocessor macro CHECK_ENABLED=1.; The pure procedure(s) documented herein become impure when the ParaMonte library is compiled with preprocessor macro CHECK_ENABLED=1.
By default, these procedures are pure in release build and impure in debug and testing builds.

Remarks: The procedures under discussion are elemental.; The choice of logSigma vs. sigma as the input argument to the procedures of this generic interface may seem rather odd.
This choice was made deliberately to increase the similarity and consistency of the functional interface here with the subroutine interface setExpGammaCDF.
Note that the primary reason for preferring logSigma vs. sigma as the choice of input argument is the enhanced computational efficiency of the routines.
Additionally, logSigma matches the alternative rate interpretation of the second parameter of the ExpGamma distribution.

See also: setExpGammaCDF

Example usage ⛓

: 1program example

2

3 use pm_kind, only: SK

4 use pm_kind, only: IK

5 use pm_kind, only: RK => RKS ! all other real kinds are also supported.

6 use pm_io, only: display_type

7 use pm_arraySpace, only: getLinSpace

8 use pm_arraySpace, only: getLogSpace

9 use pm_distExpGamma, only: getExpGammaCDF

10

11 implicit none

12

13 integer(IK) , parameter :: NP = 1000_IK

14 real(RK) , allocatable :: Point(:), CDF(:), Kappa(:), LogSigma(:)

15

16 type(display_type) :: disp

17 disp = display_type(file = "main.out.F90")

18

19 Kappa = getLinSpace(+0.5_RK, +2._RK, count = NP)

20 LogSigma = getLinSpace(-3._RK, +3._RK, count = NP)

21 Point = getLinSpace(-10._RK, +10._RK, count = NP)

22 allocate(CDF, mold = Point)

23

24 call disp%skip()

25 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

26 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

27 call disp%show("! Compute the Cumulative Distribution Function (CDF) of ExpGamma distribution at the specified values.")

28 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

29 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

30 call disp%skip()

31

32 call disp%skip()

33 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

34 call disp%show("! Compute the CDF at an input scalar real value.")

35 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

36 call disp%skip()

37

38 call disp%skip()

39 call disp%show("CDF(1) = getExpGammaCDF(0.5_RK)")

40 CDF(1) = getExpGammaCDF(0.5_RK)

41 call disp%show("CDF(1)")

42 call disp%show( CDF(1) )

43 call disp%skip()

44

45 call disp%skip()

46 call disp%show("Kappa(1)")

47 call disp%show( Kappa(1) )

48 call disp%show("CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1))")

49 CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1))

50 call disp%show("CDF(1)")

51 call disp%show( CDF(1) )

52 call disp%skip()

53

54 call disp%skip()

55 call disp%show("Kappa(1)")

56 call disp%show( Kappa(1) )

57 call disp%show("CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1))")

58 CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1))

59 call disp%show("CDF(1)")

60 call disp%show( CDF(1) )

61 call disp%skip()

62

63 call disp%skip()

64 call disp%show("Kappa(1)")

65 call disp%show( Kappa(1) )

66 call disp%show("CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1), LogSigma(1))")

67 CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1), LogSigma(1))

68 call disp%show("CDF(1)")

69 call disp%show( CDF(1) )

70 call disp%skip()

71

72 call disp%skip()

73 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

74 call disp%show("! Compute the CDF at an input vector real value with different parameter values.")

75 call disp%show("!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")

76 call disp%skip()

77

78 call disp%skip()

79 call disp%show("Kappa(1)")

80 call disp%show( Kappa(1) )

81 call disp%show("CDF(1:NP:NP/5) = getExpGammaCDF(0.5_RK, Kappa(1:NP:NP/5))")

82 CDF(1:NP:NP/5) = getExpGammaCDF(0.5_RK, Kappa(1:NP:NP/5))

83 call disp%show("CDF(1:NP:NP/5)")

84 call disp%show( CDF(1:NP:NP/5) )

85 call disp%skip()

86

87 call disp%skip()

88 call disp%show("Kappa(1)")

89 call disp%show( Kappa(1) )

90 call disp%show("CDF(1:NP:NP/5) = getExpGammaCDF(Point(1:NP:NP/5), Kappa(1:NP:NP/5))")

91 CDF(1:NP:NP/5) = getExpGammaCDF(Point(1:NP:NP/5), Kappa(1:NP:NP/5))

92 call disp%show("CDF(1:NP:NP/5)")

93 call disp%show( CDF(1:NP:NP/5) )

94 call disp%skip()

95

96 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

97 ! Output an example array for visualization.

98 !%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

99

100 block

101 integer :: fileUnit, i

102 real(RK) :: CDF(NP,6)

103 CDF(:,1) = getExpGammaCDF(Point, .5_RK, 0.5)

104 CDF(:,2) = getExpGammaCDF(Point, 1._RK, 0.5)

105 CDF(:,3) = getExpGammaCDF(Point, 2._RK, 0.5)

106 CDF(:,4) = getExpGammaCDF(Point, .5_RK, 2.0)

107 CDF(:,5) = getExpGammaCDF(Point, 1._RK, 2.0)

108 CDF(:,6) = getExpGammaCDF(Point, 2._RK, 2.0)

109 open(newunit = fileUnit, file = "getExpGammaCDF.RK.txt")

110 write(fileUnit,"(7(g0,:,' '))") (Point(i), CDF(i,:), i = 1, size(Point))

111 close(fileUnit)

112 end block

113

114end program example

pm_arraySpace::getLinSpace
Generate count evenly spaced points over the interval [x1, x2] if x1 < x2, or [x2,...
Definition: pm_arraySpace.F90:108

pm_arraySpace::getLogSpace
Generate count evenly-logarithmically-spaced points over the interval [base**logx1,...
Definition: pm_arraySpace.F90:538

pm_io::show
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11726

pm_io::skip
This is a generic method of the derived type display_type with pass attribute.
Definition: pm_io.F90:11508

pm_arraySpace
This module contains procedures and generic interfaces for generating arrays with linear or logarithm...
Definition: pm_arraySpace.F90:33

pm_io
This module contains classes and procedures for input/output (IO) or generic display operations on st...
Definition: pm_io.F90:252

pm_io::disp
type(display_type) disp
This is a scalar module variable an object of type display_type for general display.
Definition: pm_io.F90:11393

pm_kind
This module defines the relevant Fortran kind type-parameters frequently used in the ParaMonte librar...
Definition: pm_kind.F90:268

pm_kind::RK
integer, parameter RK
The default real kind in the ParaMonte library: real64 in Fortran, c_double in C-Fortran Interoperati...
Definition: pm_kind.F90:543

pm_kind::IK
integer, parameter IK
The default integer kind in the ParaMonte library: int32 in Fortran, c_int32_t in C-Fortran Interoper...
Definition: pm_kind.F90:540

pm_kind::SK
integer, parameter SK
The default character kind in the ParaMonte library: kind("a") in Fortran, c_char in C-Fortran Intero...
Definition: pm_kind.F90:539

pm_kind::RKS
integer, parameter RKS
The single-precision real kind in Fortran mode. On most platforms, this is an 32-bit real kind.
Definition: pm_kind.F90:567

pm_io::display_type
Generate and return an object of type display_type.
Definition: pm_io.F90:10282

Example Unix compile command via Intel ifort compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3ifort -fpp -standard-semantics -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example Windows Batch compile command via Intel ifort compiler ⛓
1del main.exe

2set PATH=..\..\..\lib;%PATH%

3ifort /fpp /standard-semantics /O3 /I:..\..\..\include main.F90 ..\..\..\lib\libparamonte*.lib /exe:main.exe

4main.exe

Example Unix / MinGW compile command via GNU gfortran compiler ⛓
1#!/usr/bin/env sh

2rm main.exe

3gfortran -cpp -ffree-line-length-none -O3 -Wl,-rpath,../../../lib -I../../../inc main.F90 ../../../lib/libparamonte* -o main.exe

4./main.exe

Example output ⛓
1

2!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

3!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

4! Compute the Cumulative Distribution Function (CDF) of ExpGamma distribution at the specified values.

5!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

6!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

7

8

9!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

10! Compute the CDF at an input scalar real value.

11!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

12

13

14CDF(1) = getExpGammaCDF(0.5_RK)

15CDF(1)

16+0.807704329

17

18

19Kappa(1)

20+0.500000000

21CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1))

22CDF(1)

23+0.930612206

24

25

26Kappa(1)

27+0.500000000

28CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1))

29CDF(1)

30+0.930612206

31

32

33Kappa(1)

34+0.500000000

35CDF(1) = getExpGammaCDF(0.5_RK, Kappa(1), LogSigma(1))

36CDF(1)

37+1.00000000

38

39

40!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

41! Compute the CDF at an input vector real value with different parameter values.

42!%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

43

44

45Kappa(1)

46+0.500000000

47CDF(1:NP:NP/5) = getExpGammaCDF(0.5_RK, Kappa(1:NP:NP/5))

48CDF(1:NP:NP/5)

49+0.930612206, +0.862185597, +0.778141320, +0.684153199, +0.586314142

50

51

52Kappa(1)

53+0.500000000

54CDF(1:NP:NP/5) = getExpGammaCDF(Point(1:NP:NP/5), Kappa(1:NP:NP/5))

55CDF(1:NP:NP/5)

56+0.760284485E-2, +0.883790851E-2, +0.993758515E-1, +0.998501480, +1.00000000

57

58

Postprocessing of the example output ⛓
1#!/usr/bin/env python

2

3import matplotlib.pyplot as plt

4import pandas as pd

5import numpy as np

6import glob

7import sys

8

9fontsize = 17

10

11marker ={ "CK" : "-"

12 , "IK" : "."

13 , "RK" : "-"

14 }

15xlab = { "CK" : "X ( real/imaginary components )"

16 , "IK" : "X ( integer-valued )"

17 , "RK" : "X ( real-valued )"

18 }

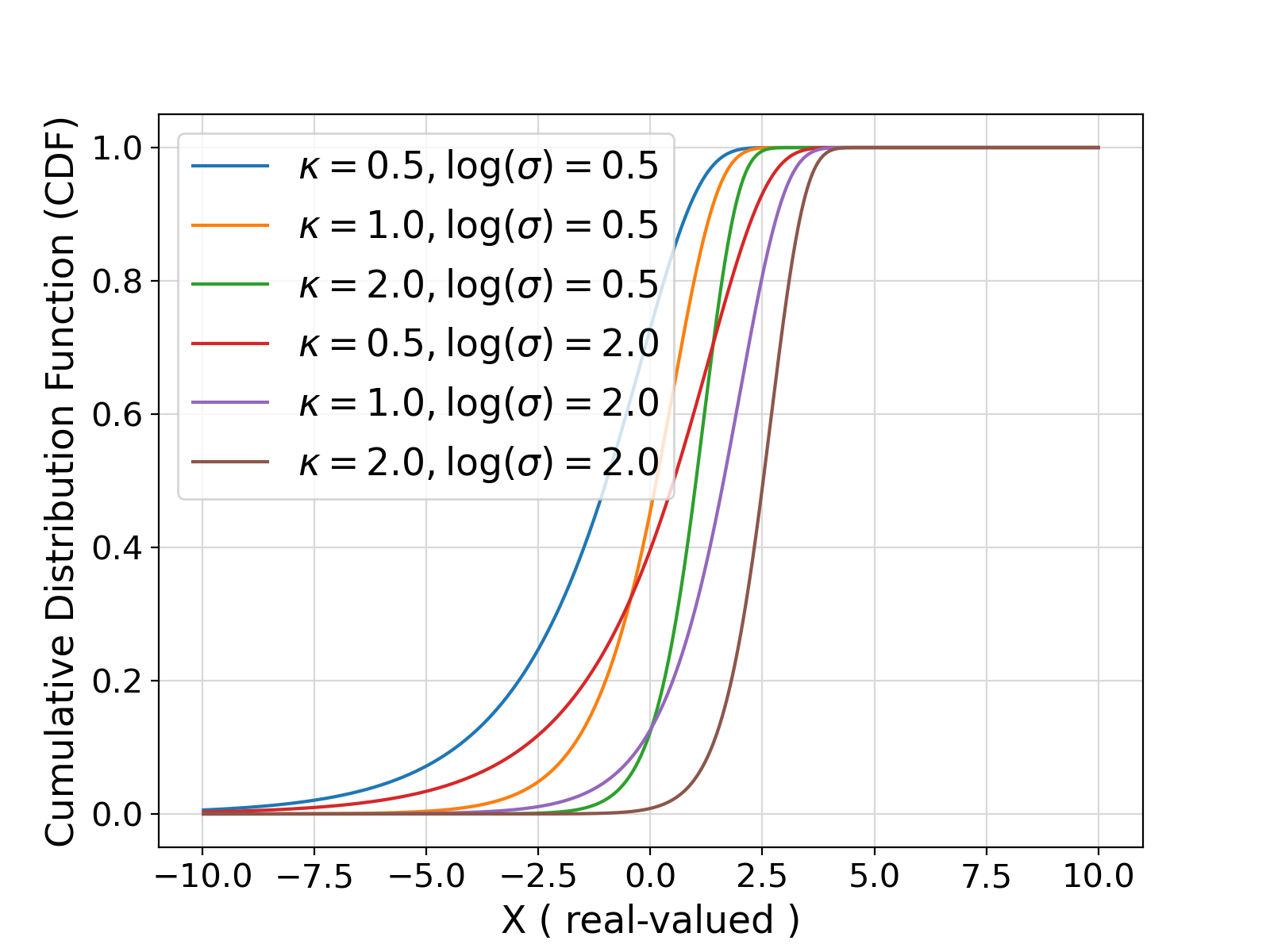
19legends = [ "$\kappa = 0.5, \log(\sigma) = 0.5$"

20 , "$\kappa = 1.0, \log(\sigma) = 0.5$"

21 , "$\kappa = 2.0, \log(\sigma) = 0.5$"

22 , "$\kappa = 0.5, \log(\sigma) = 2.0$"

23 , "$\kappa = 1.0, \log(\sigma) = 2.0$"

24 , "$\kappa = 2.0, \log(\sigma) = 2.0$"

25 ]

26

27for kind in ["IK", "CK", "RK"]:

28

29 pattern = "*." + kind + ".txt"

30 fileList = glob.glob(pattern)

31 if len(fileList) == 1:

32

33 df = pd.read_csv(fileList[0], delimiter = " ")

34

35 fig = plt.figure(figsize = 1.25 * np.array([6.4, 4.8]), dpi = 200)

36 ax = plt.subplot()

37

38 if kind == "CK":

39 plt.plot( df.values[:, 0]

40 , df.values[:,1:len(legends)+1]

41 , marker[kind]

42 #, color = "r"

43 )

44 plt.plot( df.values[:, 1]

45 , df.values[:,1:len(legends)+1]

46 , marker[kind]

47 #, color = "blue"

48 )

49 else:

50 plt.plot( df.values[:, 0]

51 , df.values[:,1:len(legends)+1]

52 , marker[kind]

53 #, color = "r"

54 )

55 ax.legend ( legends

56 , fontsize = fontsize

57 )

58

59 plt.xticks(fontsize = fontsize - 2)

60 plt.yticks(fontsize = fontsize - 2)

61 ax.set_xlabel(xlab[kind], fontsize = 17)

62 ax.set_ylabel("Cumulative Distribution Function (CDF)", fontsize = 17)

63

64 plt.grid(visible = True, which = "both", axis = "both", color = "0.85", linestyle = "-")

65 ax.tick_params(axis = "y", which = "minor")

66 ax.tick_params(axis = "x", which = "minor")

67

68 plt.savefig(fileList[0].replace(".txt",".png"))

69

70 elif len(fileList) > 1:

71

72 sys.exit("Ambiguous file list exists.")

Visualization of the example output ⛓

Test:: test_pm_distExpGamma

Todo:: Low Priority: This generic interface can be extended to complex arguments.

Final Remarks ⛓

If you believe this algorithm or its documentation can be improved, we appreciate your contribution and help to edit this page's documentation and source file on GitHub.
For details on the naming abbreviations, see this page.
For details on the naming conventions, see this page.
This software is distributed under the MIT license with additional terms outlined below.

If you use any parts or concepts from this library to any extent, please acknowledge the usage by citing the relevant publications of the ParaMonte library.
If you regenerate any parts/ideas from this library in a programming environment other than those currently supported by this ParaMonte library (i.e., other than C, C++, Fortran, MATLAB, Python, R), please also ask the end users to cite this original ParaMonte library.

This software is available to the public under a highly permissive license.
Help us justify its continued development and maintenance by acknowledging its benefit to society, distributing it, and contributing to it.

Copyright: Computational Data Science Lab

Author:: Amir Shahmoradi, Oct 16, 2009, 11:14 AM, Michigan

Definition at line 720 of file pm_distExpGamma.F90.

The documentation for this interface was generated from the following file:

src/fortran/main/pm_distExpGamma.F90